2.1.4 多项式的乘法 课件 (1)
文档属性
| 名称 | 2.1.4 多项式的乘法 课件 (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 21:46:46 | ||
图片预览






文档简介
课件20张PPT。 2.1.4 多项式的乘法
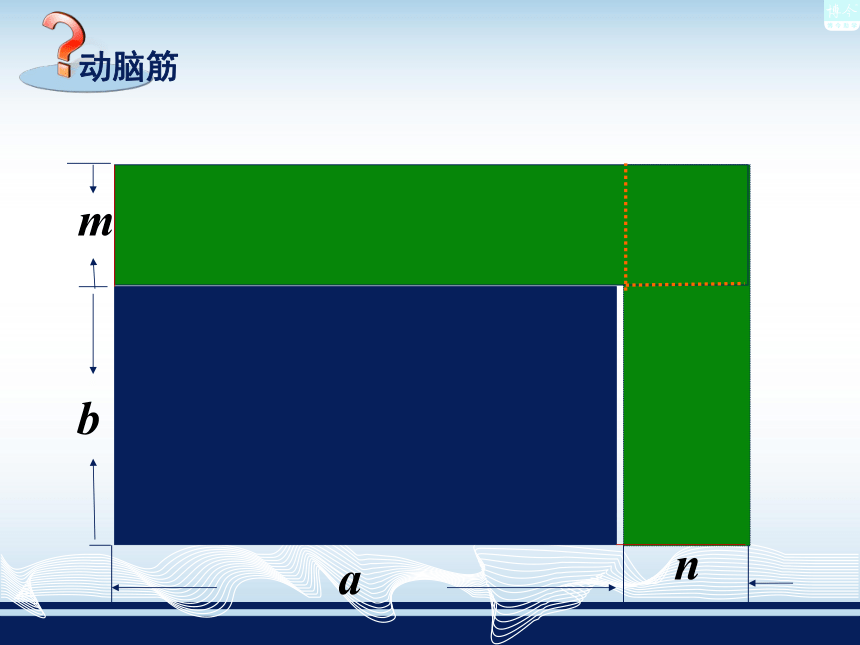
——多项式乘多项式2.为了扩大花园的绿地面积,把一块原长a米,宽为b米的长方形绿地,增长 n米,加宽m米。
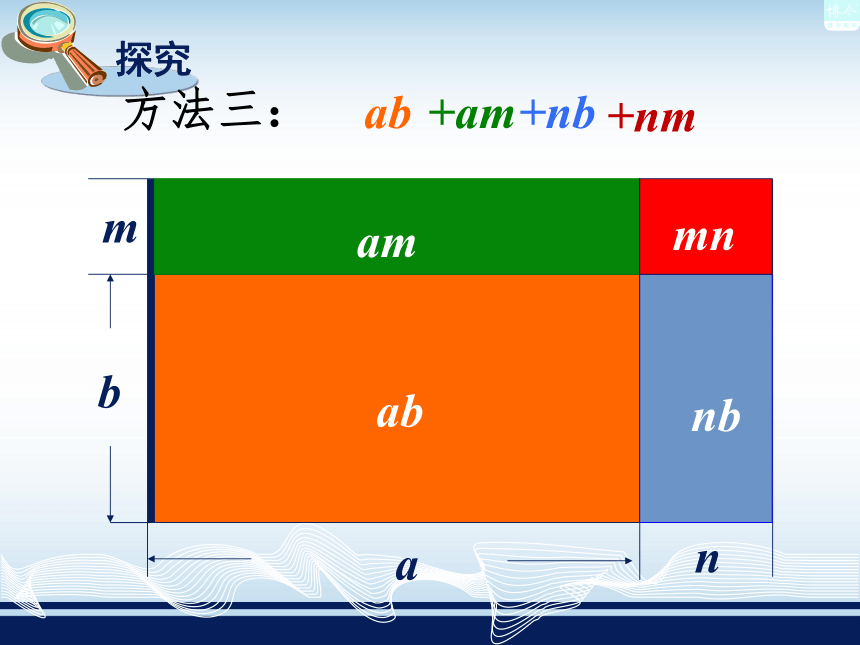
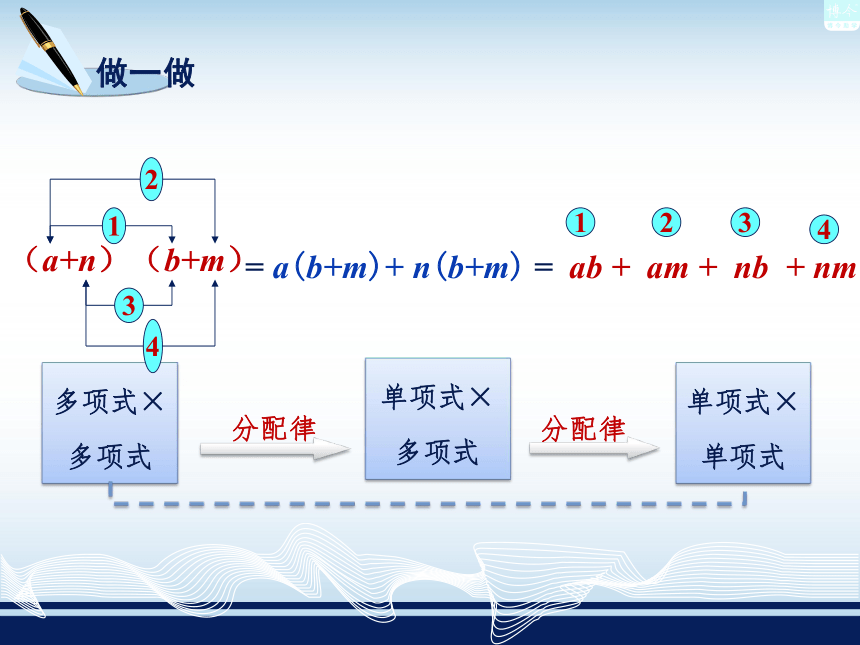
问题:你能用几种方法求出扩大后的总面积?1.已知a·(b+m)= 如果将a换成(a+n),你能计算(a+n)·(b+m) 吗?ab+amm banb+ma+n(a+n)(b+m)方法一:ab+mna(b+m)n(b+m)a(b+m)+n(b+m)方法二:mbanammnabnb方法三:(a+n)(b+m)= ab + am + nb + nm分配律分配律多项式×
多项式单项式×
多项式单项式×
单项式1234 = a(b+m)+ n(b+m) 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即:多项式乘法法则:(a+n)(b+m)=ab+am+nb+nm.这个运算过程可表示为:( a + b )( m + n )= abmn+ a+ mb+ n 从同一面积的不同表达式入手,借助分配律得到多项式的乘法法则. 由法则可知:(1)多项式与多项式相乘的结果仍是________。多项式 (2)结果的项数应该是原两个多项式________(没有经过合并同类项之前),检验项数常常作为检验解题过程是否的一个有效方法.项数的积例 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b).(1) (2x+y)(x-3y)解:原式= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解:原式= 6x3-2x2–10x+3x2 -x-5 = 6x3 + x2-11x - 5.在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。多项式与多项式相乘的结果仍是多项式。多项式乘以多项式,展开后项数有什么规律?(1)不要漏项;
(2)要注意符号,可以先确定符号再乘积;
(3)多项式与多项式相乘的结果中,要把同类项合并。
注意些什么?解(1)(a+b)(a-b) = a2-ab+ba-b2 = a2-b2= (a+b)(a+b) = a2+ab+ba+b2 (2)(a+b)2 = a2+2ab+b2例2. (1)(a+b)(a-b) (2)
课堂总结:1.多项式乘多项式的法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.表达式: (a+n)(b+m)=ab+am+nb+nm1)不要漏项;
2)要注意符号,可以先确定符号再乘积;
3)多项式与多项式相乘的结果中,要把同类项合并。2.做题时该注意反思:1.这节课学到了什么知识?
该注意些什么? 2.还存在什么疑惑?作业:P41 第9题观察下列各式的计算结果与相乘的两个多项式之间的关系:
(x+2)(x+3)=x2+5x+6;
(x+4)(x+2)=x2+6x+8;
(x+6)(x+5)=x2+11x+30.
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+( + )x + × . 3535(3) 化简:2(x-8)(x-5)-(2x-1)(x+2)解:原式= 2(x2-13x+40)-(2x2+3x-2)
= 2x2-26x+80-2x2-3x+2
= -29x+82(2)你能很快说出与(x+a)(x+b)相等的多项式吗?(x+a)(x+b)=x2+(a+b)x+ab谢 谢
——多项式乘多项式2.为了扩大花园的绿地面积,把一块原长a米,宽为b米的长方形绿地,增长 n米,加宽m米。
问题:你能用几种方法求出扩大后的总面积?1.已知a·(b+m)= 如果将a换成(a+n),你能计算(a+n)·(b+m) 吗?ab+amm banb+ma+n(a+n)(b+m)方法一:ab+mna(b+m)n(b+m)a(b+m)+n(b+m)方法二:mbanammnabnb方法三:(a+n)(b+m)= ab + am + nb + nm分配律分配律多项式×
多项式单项式×
多项式单项式×
单项式1234 = a(b+m)+ n(b+m) 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即:多项式乘法法则:(a+n)(b+m)=ab+am+nb+nm.这个运算过程可表示为:( a + b )( m + n )= abmn+ a+ mb+ n 从同一面积的不同表达式入手,借助分配律得到多项式的乘法法则. 由法则可知:(1)多项式与多项式相乘的结果仍是________。多项式 (2)结果的项数应该是原两个多项式________(没有经过合并同类项之前),检验项数常常作为检验解题过程是否的一个有效方法.项数的积例 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b).(1) (2x+y)(x-3y)解:原式= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解:原式= 6x3-2x2–10x+3x2 -x-5 = 6x3 + x2-11x - 5.在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。多项式与多项式相乘的结果仍是多项式。多项式乘以多项式,展开后项数有什么规律?(1)不要漏项;
(2)要注意符号,可以先确定符号再乘积;
(3)多项式与多项式相乘的结果中,要把同类项合并。
注意些什么?解(1)(a+b)(a-b) = a2-ab+ba-b2 = a2-b2= (a+b)(a+b) = a2+ab+ba+b2 (2)(a+b)2 = a2+2ab+b2例2. (1)(a+b)(a-b) (2)
课堂总结:1.多项式乘多项式的法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.表达式: (a+n)(b+m)=ab+am+nb+nm1)不要漏项;
2)要注意符号,可以先确定符号再乘积;
3)多项式与多项式相乘的结果中,要把同类项合并。2.做题时该注意反思:1.这节课学到了什么知识?
该注意些什么? 2.还存在什么疑惑?作业:P41 第9题观察下列各式的计算结果与相乘的两个多项式之间的关系:
(x+2)(x+3)=x2+5x+6;
(x+4)(x+2)=x2+6x+8;
(x+6)(x+5)=x2+11x+30.
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+( + )x + × . 3535(3) 化简:2(x-8)(x-5)-(2x-1)(x+2)解:原式= 2(x2-13x+40)-(2x2+3x-2)
= 2x2-26x+80-2x2-3x+2
= -29x+82(2)你能很快说出与(x+a)(x+b)相等的多项式吗?(x+a)(x+b)=x2+(a+b)x+ab谢 谢
