2.1.4 多项式的乘法 课件 (3)
图片预览



文档简介
课件28张PPT。复习:① 将单项式分别乘以多项式的各项,② 再把所得的积相加。即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.① 不能漏乘:计算:(1)(-3x3y)(-5x4y2z4)=_______;
(2)-3ab2(-4a+3ab-2)
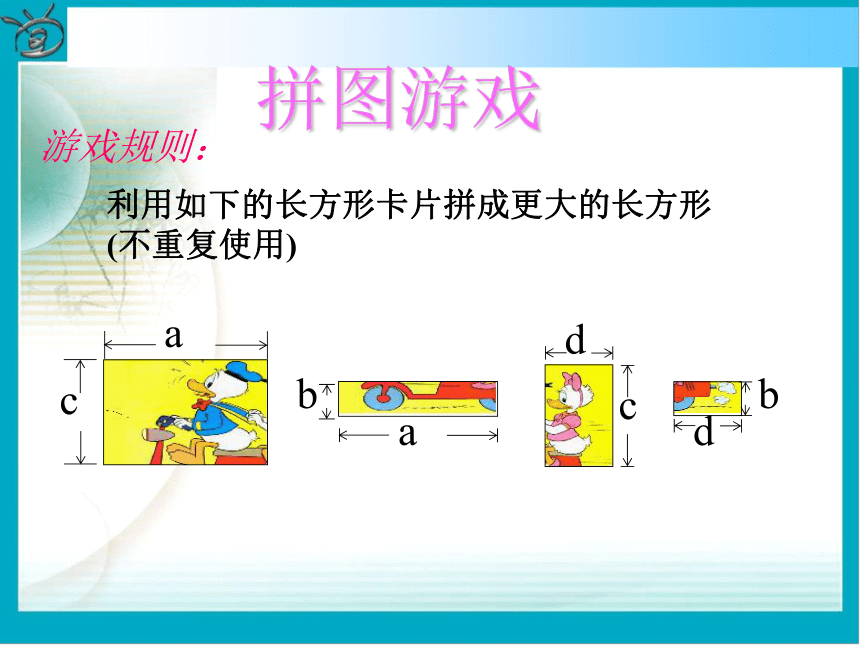
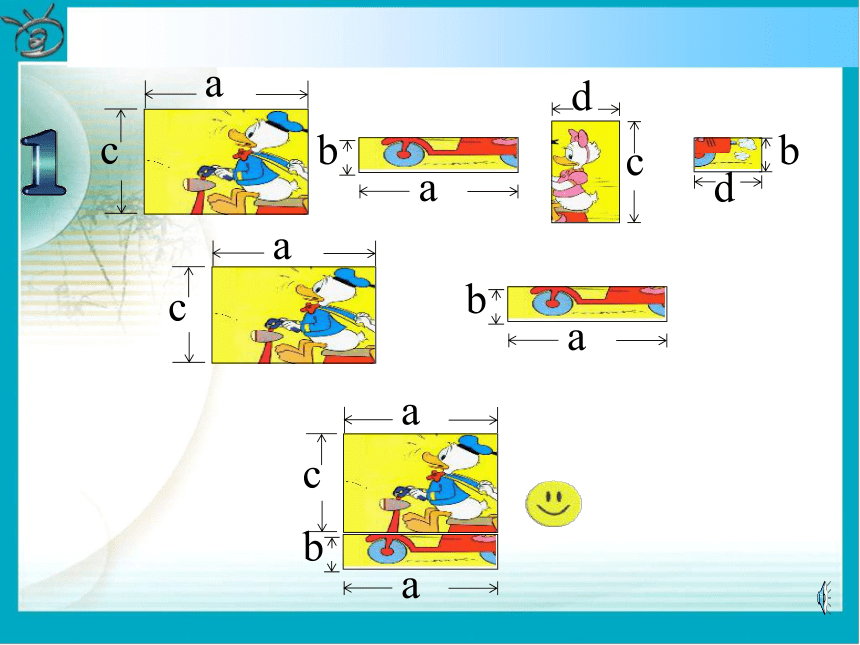
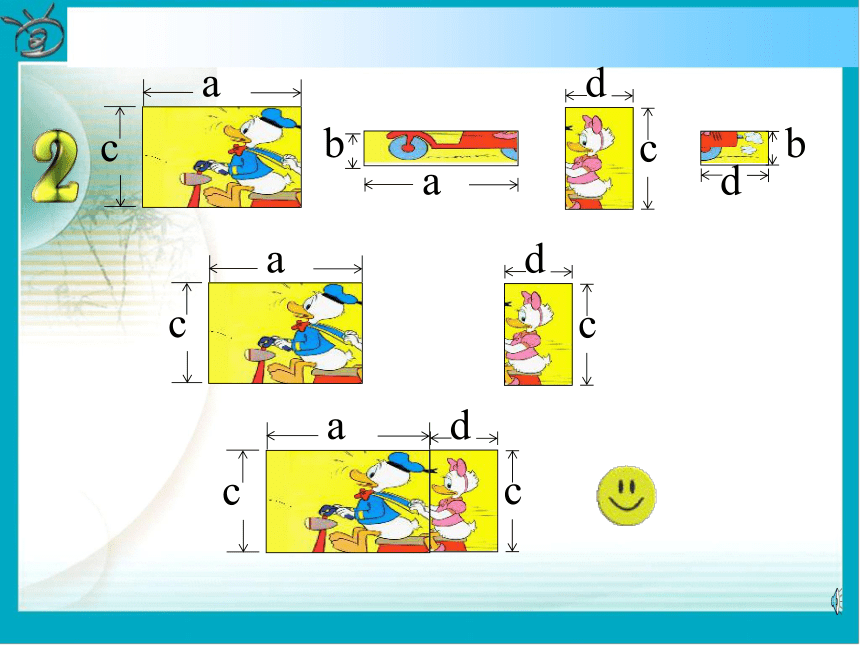
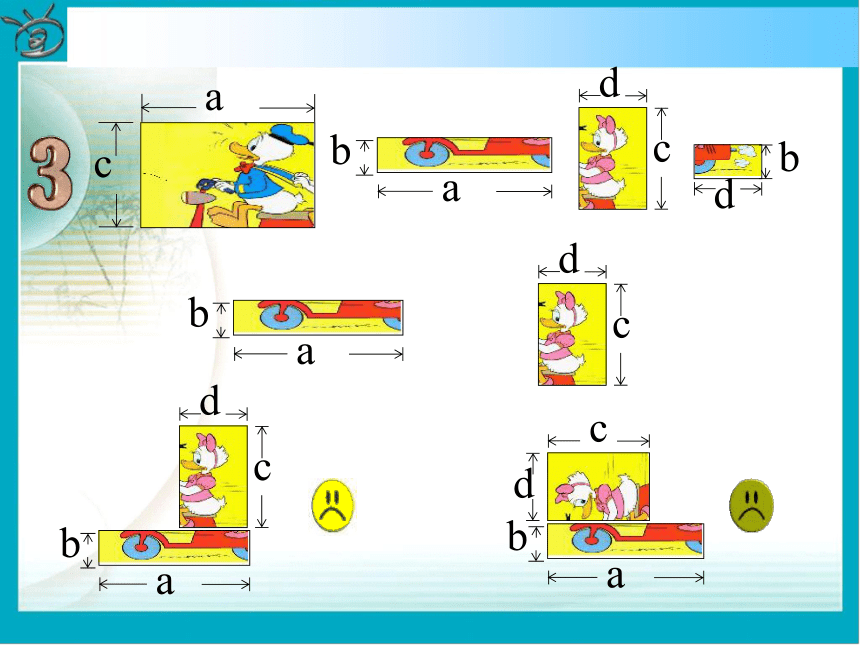
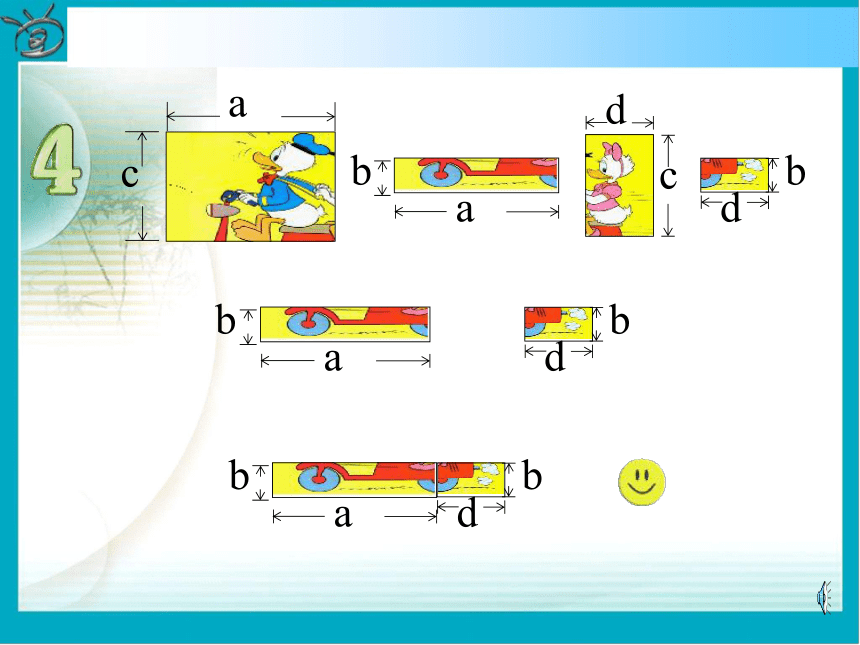
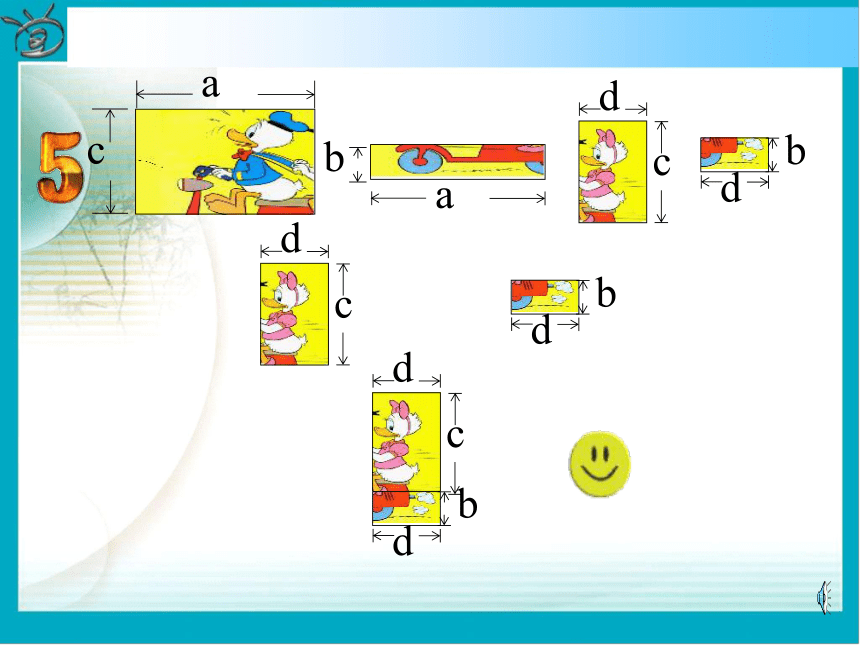
=________________15x7y3z412a2b2-9a2b3+6ab2拼图游戏游戏规则:利用如下的长方形卡片拼成更大的长方形(不重复使用) 〈问题〉你能用不同的形式表示6号图形的面积 吗?并说明理由。a(c+b)(1) d(c+b) + a(c+b)(1) d(c+b) + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3) ac ba dc bd + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3)ac ba dc +bd ++ + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3) ac + ba + dc + bd(c+b) (a+d)(4)由于(1) (3)(4)均表示6号图形的面积,于是得:(一)(c+b)(a+d) =a(c+b)+d(c+b)=ac+ab+dc+db或由(2)(3)(4)得(c+b)(a+d)=c(a+d)+b(a+d)=ac+cd+ab+bd(二)议一议对于上式(一)(二)你能说出每步的根据吗?明晰:每步均利用乘法分配律得到,把一个多项式看成一个整体,运用单项式与多项式相乘的法则,将这个整体去和另一个多项式中的每一项都相乘 。综合(一)(二)讨论:(a+d)(c+b)=ac+ab+dc+db从等式左边到右边你发现了什么规律?ⅠⅠⅡⅡⅢⅢⅣⅣ多项式的乘法法则 多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.例1 计算: 解: 分别相乘注意符号乘方要写成乘积进行运算熟练后此步骤可省略最后的结果要合并同类项按法则运算温馨提示: 1.运用多项式的乘法法则时,必须做到不重不漏. 多项式与多项式相乘,仍得多项式.两个多项式相乘合并同类项之前的项数应等于这两个多项式的项数的乘积。
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式相乘的展开式中,有同类项要合并同类项. 做一做:(1) (2n+6)(n–3);(2) (2x+5) 2例2 计算: 解: 底数不变,指数相加合并同类项例3 计算: 解: 注意运算顺序去括号时注意符号合并同类项分别相乘(1)(2)答案:1、法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
2、需要注意的几个问题
(1)漏乘
(2)符号问题
(3)最后结果应化成最简形式这节课,我的收获是---作 业A组 8 、 9谢谢大家!
(2)-3ab2(-4a+3ab-2)
=________________15x7y3z412a2b2-9a2b3+6ab2拼图游戏游戏规则:利用如下的长方形卡片拼成更大的长方形(不重复使用) 〈问题〉你能用不同的形式表示6号图形的面积 吗?并说明理由。a(c+b)(1) d(c+b) + a(c+b)(1) d(c+b) + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3) ac ba dc bd + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3)ac ba dc +bd ++ + a(c+b)(1) d(c+b)b(a+d)c(a+d)(2) + (3) ac + ba + dc + bd(c+b) (a+d)(4)由于(1) (3)(4)均表示6号图形的面积,于是得:(一)(c+b)(a+d) =a(c+b)+d(c+b)=ac+ab+dc+db或由(2)(3)(4)得(c+b)(a+d)=c(a+d)+b(a+d)=ac+cd+ab+bd(二)议一议对于上式(一)(二)你能说出每步的根据吗?明晰:每步均利用乘法分配律得到,把一个多项式看成一个整体,运用单项式与多项式相乘的法则,将这个整体去和另一个多项式中的每一项都相乘 。综合(一)(二)讨论:(a+d)(c+b)=ac+ab+dc+db从等式左边到右边你发现了什么规律?ⅠⅠⅡⅡⅢⅢⅣⅣ多项式的乘法法则 多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.例1 计算: 解: 分别相乘注意符号乘方要写成乘积进行运算熟练后此步骤可省略最后的结果要合并同类项按法则运算温馨提示: 1.运用多项式的乘法法则时,必须做到不重不漏. 多项式与多项式相乘,仍得多项式.两个多项式相乘合并同类项之前的项数应等于这两个多项式的项数的乘积。
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式相乘的展开式中,有同类项要合并同类项. 做一做:(1) (2n+6)(n–3);(2) (2x+5) 2例2 计算: 解: 底数不变,指数相加合并同类项例3 计算: 解: 注意运算顺序去括号时注意符号合并同类项分别相乘(1)(2)答案:1、法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
2、需要注意的几个问题
(1)漏乘
(2)符号问题
(3)最后结果应化成最简形式这节课,我的收获是---作 业A组 8 、 9谢谢大家!
