2.1.4 多项式的乘法 课件 (4)
文档属性
| 名称 | 2.1.4 多项式的乘法 课件 (4) |

|
|
| 格式 | zip | ||
| 文件大小 | 992.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 21:48:19 | ||
图片预览





文档简介
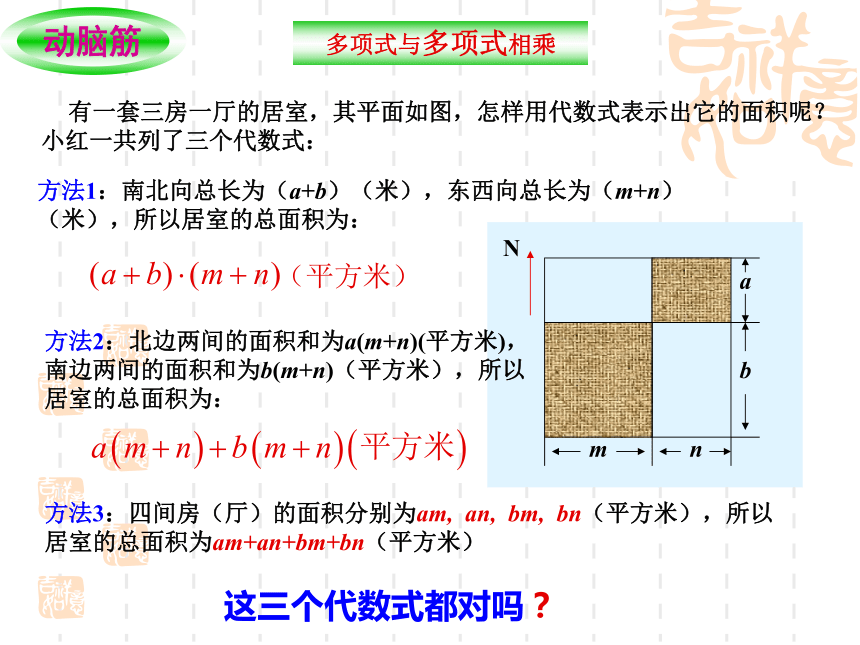
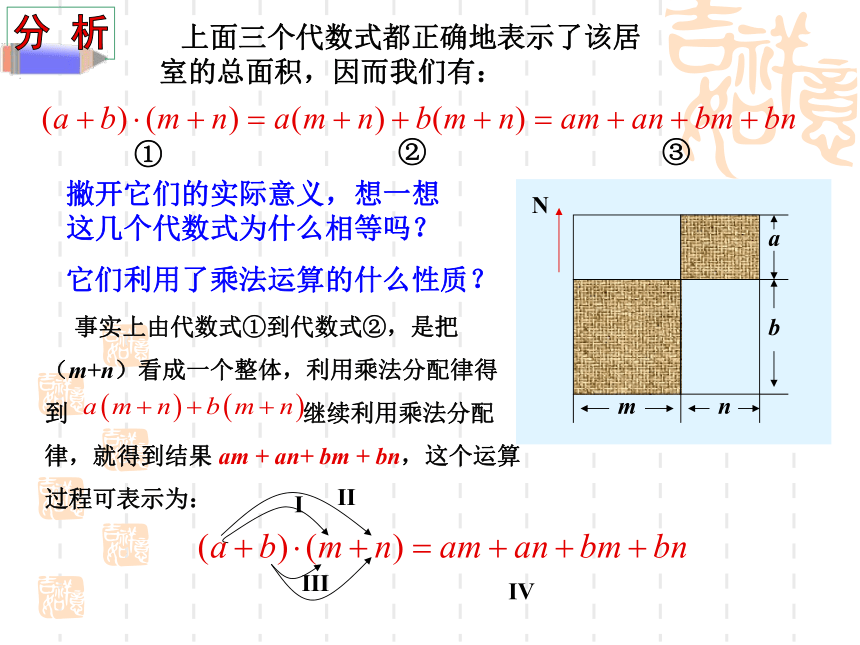
课件15张PPT。 2.1.4 多项式的乘法(第2课时)同学们看(4)这道题怎样做?它和我们以前所学的有何不同? 计算:多项式与多项式相乘 有一套三房一厅的居室,其平面如图,怎样用代数式表示出它的面积呢?小红一共列了三个代数式:方法1:南北向总长为(a+b)(米),东西向总长为(m+n)(米),所以居室的总面积为:方法2:北边两间的面积和为a(m+n)(平方米),南边两间的面积和为b(m+n)(平方米),所以居室的总面积为:Nnmba方法3:四间房(厅)的面积分别为am, an, bm, bn(平方米),所以居室的总面积为am+an+bm+bn(平方米)这三个代数式都对吗? (平方米) 上面三个代数式都正确地表示了该居 室的总面积,因而我们有: 事实上由代数式①到代数式②,是把
(m+n)看成一个整体,利用乘法分配律得
到 继续利用乘法分配
律,就得到结果 am + an+ bm + bn,这个运算
过程可表示为:Nnmba撇开它们的实际意义,想一想这几个代数式为什么相等吗?它们利用了乘法运算的什么性质?IIIIIIIV多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加. 计算 :解计算:解多项式乘以多项式防止以下错误:1、漏乘多项式中的某一项;2、某一项的符号出现错误。计算:解1.下列计算对不对?,如果不对,应怎样改正?解解观察下列各式的计算结果与相乘的两个
多项式之间的关系:
(x+2)(x+3)=x2+5x+6
(x+4)(x+2)=x2+6x+8
(x+6)(x+5)=x2+11x+30
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+(_+_)x +_×_(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
先猜一猜,再用多项式相乘的运算法则验证.3535计算:解
1、若(x+a)(x+b)中不含x的一次项,则a与b的关系是 ( )
(A)a=b=0 (B)a-b=0
(C)a=b≠0 (D)a+b=0D2、化简:2(x-8)(x-5)-(2x-1)(x+2)注意:若含有数与多项式的积相乘的运算,或者含有与多项式的积的差的运算时:
多项式乘积的展开式要用括号括起来.IIIIIIIV多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加. 本节课你有什么收获?本节课你还有什么疑问?1.计算:2.计算:
(m+n)看成一个整体,利用乘法分配律得
到 继续利用乘法分配
律,就得到结果 am + an+ bm + bn,这个运算
过程可表示为:Nnmba撇开它们的实际意义,想一想这几个代数式为什么相等吗?它们利用了乘法运算的什么性质?IIIIIIIV多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加. 计算 :解计算:解多项式乘以多项式防止以下错误:1、漏乘多项式中的某一项;2、某一项的符号出现错误。计算:解1.下列计算对不对?,如果不对,应怎样改正?解解观察下列各式的计算结果与相乘的两个
多项式之间的关系:
(x+2)(x+3)=x2+5x+6
(x+4)(x+2)=x2+6x+8
(x+6)(x+5)=x2+11x+30
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+(_+_)x +_×_(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
先猜一猜,再用多项式相乘的运算法则验证.3535计算:解
1、若(x+a)(x+b)中不含x的一次项,则a与b的关系是 ( )
(A)a=b=0 (B)a-b=0
(C)a=b≠0 (D)a+b=0D2、化简:2(x-8)(x-5)-(2x-1)(x+2)注意:若含有数与多项式的积相乘的运算,或者含有与多项式的积的差的运算时:
多项式乘积的展开式要用括号括起来.IIIIIIIV多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加. 本节课你有什么收获?本节课你还有什么疑问?1.计算:2.计算:
