2.2.1平方差公式 课件 (2)
图片预览





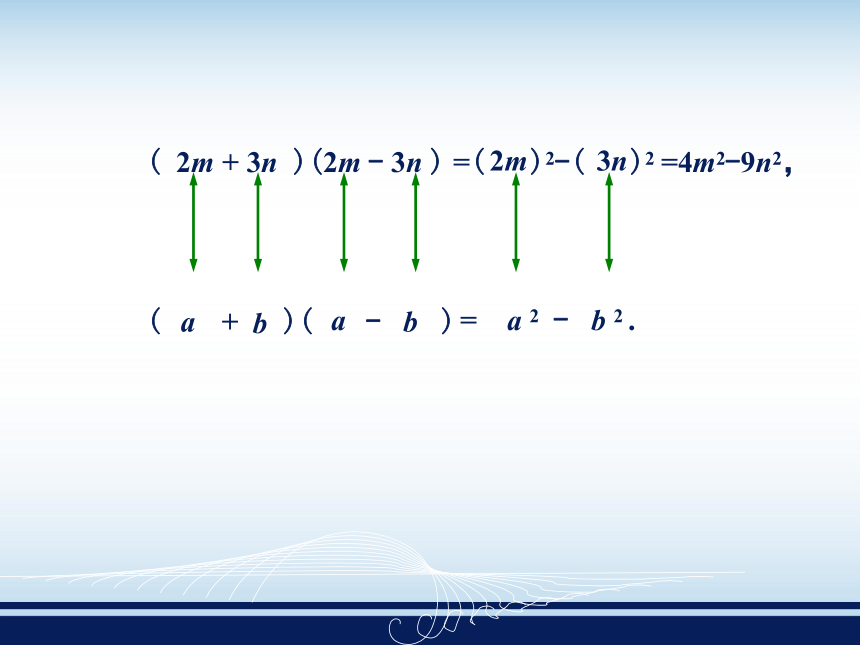


文档简介
课件21张PPT。乘法公式2.2——2.2.1 平方差公式计算下列各式,你能发现什么规律:(a + 2 )( a – 2) = a2- 2a + 2a - 22= ,= ,(a + 1 )( a - 1) = a2- a + a - 12(a + 3 )( a - 3) = a2- 3a + 3a -32= ,(a + 4 )( a - 4 ) = a2- 4a + 4a -42= .a2- 12a2- 22a2- 32a2-42我们用多项式乘法来推导一般情况( a + b )( a - b )= a2 - ab + ab - b2 = a2 - b2 .叫做平方差公式. 即两个数的和与这两个数的差的积等于这两个数的平方差.你觉得这个公式有什么特征?在使用这个公式时应该注意什么?等式左边是两数的和与两数差的乘积,右边是两数的平方和。
找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b总结出平方差公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时
更加快速和简便(a+b)(a-b)= a2 -b2 .即:相乘的两个括号中有一对相同的数(式子),有一对互为相反数的数(式子)
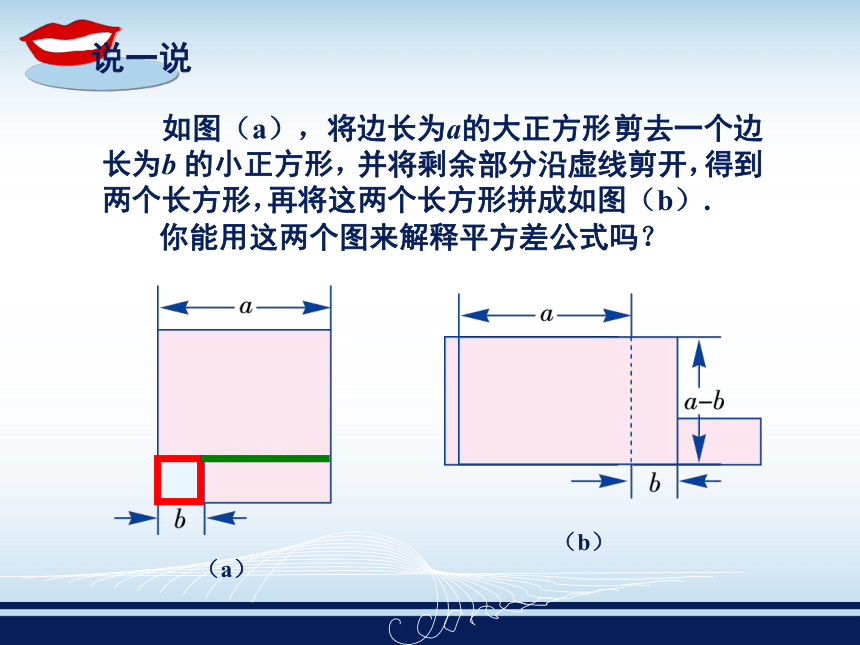
你能快速算出多项式(2m+3n)与多项式(2m-3n)的乘积吗?可以这样做! 如果把2m与3n分别看成上式的a与b,不就可以直接得到结果吗? ( 2m + 3n )(2m - 3n ) ( + )( - )a b a b = a 2 - b 2 .2m3n=( )2-( )2=4m2-9n2, 如图(a),将边长为a的大正方形 剪去一个边长为b 的小正方形, 并将剩余部分沿虚线剪开, 得到两个长方形, 再将这两个长方形拼成如图(b). 你能用这两个图来解释平方差公式吗? 对于满足平方差公式特征的多项式的乘法,可以利用该公式进行简便计算.例1 运用平方差公式计算:
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y). (1)(2x+1)(2x-1) (2)(x+2y)(x-2y)解 (2x+1)(2x-1)= (2x)2-12= 4x2-1.解 (x+2y)(x-2y)= x2 -(2y)2 = x2 -4y2例2 运用平方差公式计算:
( 1 ) ;
( 2 ) (4a+b)(-b+4a).( 3 ) (x-y)(-y-x)
(2)(4a+b)(-b+4a)解 (4a+b)(-b+4a)= (4a)2 -b2 = 16a2 -b2= (4a+b)(4a-b) 例3 计算:
1 002 × 998 .解 1 002 × 998 = (1 000 +2)(1 000-2)= 1 0002 -22= 1 000 000 - 4= 999 9961. 下面各式的计算对不对?如果不对,应怎样改正 ?(1)(x-2)(x+2)=x2-2;(2)(-2x-1)(2x-1)=4x2-1.答:不对,应是:x2-4.答:不对.
应是:1-4x22. 运用平方差公式计算:
(1)(m+2n)(m-2n);
(2)(3a+b)(3a-b);
(3)
(4)(-1+5a)(-1-5a). 解(1) (m+2n)(m-2n)
= m2-4n2
(2) (3a+b)(3a-b)
= 9a2-b2
(3)
(4) (-1+5a)(-1-5a)
= 1-25a2.3. 计算:(1) 202×198; (2) 49.8×50.2 .答案:39 996答案:2 499.96例1计算(x-y)(-y-x)的结果是( )
A. -x2+y2 B. -x2-y2
C. x2-y2 D. x2+y2A例1下列运算中正确的是 ( ).
A. x5+x5=2x10
B. -(-x)3·(-x)5= -x8
C. (-2x2y)3·4x-3=-24x3y3
D.B结 束
找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b总结出平方差公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时
更加快速和简便(a+b)(a-b)= a2 -b2 .即:相乘的两个括号中有一对相同的数(式子),有一对互为相反数的数(式子)
你能快速算出多项式(2m+3n)与多项式(2m-3n)的乘积吗?可以这样做! 如果把2m与3n分别看成上式的a与b,不就可以直接得到结果吗? ( 2m + 3n )(2m - 3n ) ( + )( - )a b a b = a 2 - b 2 .2m3n=( )2-( )2=4m2-9n2, 如图(a),将边长为a的大正方形 剪去一个边长为b 的小正方形, 并将剩余部分沿虚线剪开, 得到两个长方形, 再将这两个长方形拼成如图(b). 你能用这两个图来解释平方差公式吗? 对于满足平方差公式特征的多项式的乘法,可以利用该公式进行简便计算.例1 运用平方差公式计算:
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y). (1)(2x+1)(2x-1) (2)(x+2y)(x-2y)解 (2x+1)(2x-1)= (2x)2-12= 4x2-1.解 (x+2y)(x-2y)= x2 -(2y)2 = x2 -4y2例2 运用平方差公式计算:
( 1 ) ;
( 2 ) (4a+b)(-b+4a).( 3 ) (x-y)(-y-x)
(2)(4a+b)(-b+4a)解 (4a+b)(-b+4a)= (4a)2 -b2 = 16a2 -b2= (4a+b)(4a-b) 例3 计算:
1 002 × 998 .解 1 002 × 998 = (1 000 +2)(1 000-2)= 1 0002 -22= 1 000 000 - 4= 999 9961. 下面各式的计算对不对?如果不对,应怎样改正 ?(1)(x-2)(x+2)=x2-2;(2)(-2x-1)(2x-1)=4x2-1.答:不对,应是:x2-4.答:不对.
应是:1-4x22. 运用平方差公式计算:
(1)(m+2n)(m-2n);
(2)(3a+b)(3a-b);
(3)
(4)(-1+5a)(-1-5a). 解(1) (m+2n)(m-2n)
= m2-4n2
(2) (3a+b)(3a-b)
= 9a2-b2
(3)
(4) (-1+5a)(-1-5a)
= 1-25a2.3. 计算:(1) 202×198; (2) 49.8×50.2 .答案:39 996答案:2 499.96例1计算(x-y)(-y-x)的结果是( )
A. -x2+y2 B. -x2-y2
C. x2-y2 D. x2+y2A例1下列运算中正确的是 ( ).
A. x5+x5=2x10
B. -(-x)3·(-x)5= -x8
C. (-2x2y)3·4x-3=-24x3y3
D.B结 束
