2.2.1平方差公式 课件 (3)
图片预览








文档简介
课件27张PPT。平方差公式(m+a)(n+b)= 如果m=n,且都用 x 表示,那么上式就成为:多项式乘法
法则是: 用一个多项式的每一项 乘另一个多项式的每一项再把所得的积相加。mn+mb+an+ab =(x+a)(x+b)x2+(a+b)x+ab 这是上一节学习的
一种特殊多项式的乘法—— 两个相同字母的
二项式的乘积 .这就是从本课起要学习的内容. 计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y22、你能用语言叙述这个规律是? 两个数的和与这两个数的差的积,等于这两个数的平方差。 思考:1、你能用具有一般性的字母表达式表示这一规律吗? (a+b)(a-b) = a2 - b2思考:你能用我们学过的整式乘法的知识说明 (a+b)(a-b) = a2 –b2 这一公式的成立吗?
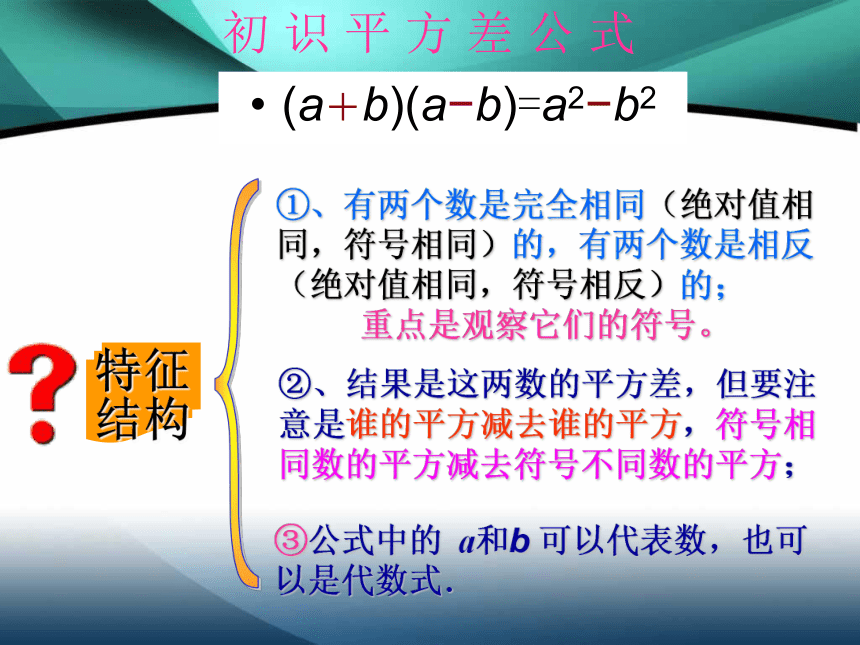
∵(a+b)(a-b) 我们把 (a+b)(a-b) = a2 –b2 这个规律叫做平方差公式=a2-ab + ab -b2 = a2 – b2∴(a+b)(a-b) =a2 – b2 只要我们能够从等式的一边推出另一边即可。初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 ①、有两个数是完全相同(绝对值相同,符号相同)的,有两个数是相反(绝对值相同,符号相反)的;
重点是观察它们的符号。②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;③公式中的 a和b 可以代表数,也可以是代数式. 例题解析例题 例1 利用平方差公式计算:
(1) (5+6x)(5?6x);(2) (x+2y)(x?2y); 解: (1) (5+6x)(5?6x)=55第一数a52?要用括号把这个数整个括起来, 再平方; ( )26x=25? 最后的结果又要去掉括号。 36x2 ;(2) (x+2y) (x?2y)
=x2?( )22y=x2 ?4y2 ;练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(m+8)(m-8) 练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(a+8)(a-8) 练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(a+b)(a-b) 练习1.运用平方差公式计算:分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(m+8)(m-8)=
(a+b) (a-b)(2a+5b)(2a-5b)== a2 - b2
(a + b) (a - b)(2a)2-(5b)2=4a2-25b2m2 –82= m2-64= a2 - b2(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。练习2.例2下列各题能否用平方差公式计算,请说明理由,并计算。 (1)(4y+3x)(3x-4y)(加法交换律)解:=(3x+4y)(3x-4y)=(3x)2-(4y)2=9x2-16y2(2)(-4a-b)(4a-b)(加法交换律)解:(-4a-b)(4a-b)
=(-b-4a)(-b+4a)
= (-b)2-(4a)2
= b2-16a2
(-4a-b)(4a-b)(分配律的逆运用)= -(4a+b)(4a-b)= -[(4a)2 -b2]= -(16a2 -b2)= b2 -16a2(3)59.8 × 60.2 解: 59.8 × 60.2(观察数字特点)=(60-0.2)(60+0.2)=602-(0.2)2
=3600-0.04
=3599.96
平方差公式⑷、利用平方差公式计算:1998×2002技巧小结:如何找符合公式(a+b)(a-b)的a和b
把它们的平均数作a,把两数差的一半作b, 平方差公式常用变化形式:①位置变化:②符号变化:③指数变化:④系数变化:⑤数字变化:平方差公式分层练习:A组:判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y) ( )
2、(a-2b)(-a-2b) ( )
3、(-2m-n)(n + 2m) ( )
4、(2c-b)( -b-2c) ( )
B组:1、计算:
(2x+ )(2x- ) (-x+2)(-x-2)
?
(-2x+y)(2x+y) (y-x)(-x-y)
?
2、简便计算:
?(1)498×502 (2)999×1001C组:
1、[(a+b)+(a-b)][(a+b)-(a-b)]
2 、[(a+b)(a-b)] 3、(2x+y+5)(2x+y-5)
思考:(a+b+c)(a-b-c)= ?
4、(x-1)(x2 +1)(x+1)
5、(a-3)(a+4)(a+3)(a-4)
?
6、(2a-5b)(2a+5b)(4a2+25b2)
7、20042-2005×2003平方差公式平方差公式拓展:计算(用指数形式表示)
1、(x-1)(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
?
2、(2+1) (22+1)(24+1) (28+1) (216+1)
?
3、(x+1) (x2+1)(x4+1) (x8+1) (x16+1) 平方差公式常用变化形式:①位置变化:②符号变化:③指数变化:④系数变化:⑤数字变化:⑥增项变化:⑦增因式变化:⑧连用公式变化:平方差公式平方差公式平方差公式的几何背景:请同学们思考如何用几何图形的
面积来解释(a +b)(a-b)呢? 1、当a>b>0时,我们可能看成是以长为(a+b) ,
宽为(a-b)的长方形的面积。 2、如何解释公式的右端:
a2-b2小结试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式; 要利用加法交换律,对于不符合平方差公式标准形式者,
法则是: 用一个多项式的每一项 乘另一个多项式的每一项再把所得的积相加。mn+mb+an+ab =(x+a)(x+b)x2+(a+b)x+ab 这是上一节学习的
一种特殊多项式的乘法—— 两个相同字母的
二项式的乘积 .这就是从本课起要学习的内容. 计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y2计算下列各题(1)(a+5)(a-5)=
(2)(m+3) (m-3)=
(3)(3x+7)(3x-7)=
(4)(5a+b)(5a-b)=
(5)(n+3m)(n-3m)=
(6)(x+2y)(x-2y)= a2-25m2-99x2-4925a2-b2n2-9m2x2-4y22、你能用语言叙述这个规律是? 两个数的和与这两个数的差的积,等于这两个数的平方差。 思考:1、你能用具有一般性的字母表达式表示这一规律吗? (a+b)(a-b) = a2 - b2思考:你能用我们学过的整式乘法的知识说明 (a+b)(a-b) = a2 –b2 这一公式的成立吗?
∵(a+b)(a-b) 我们把 (a+b)(a-b) = a2 –b2 这个规律叫做平方差公式=a2-ab + ab -b2 = a2 – b2∴(a+b)(a-b) =a2 – b2 只要我们能够从等式的一边推出另一边即可。初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 ①、有两个数是完全相同(绝对值相同,符号相同)的,有两个数是相反(绝对值相同,符号相反)的;
重点是观察它们的符号。②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;③公式中的 a和b 可以代表数,也可以是代数式. 例题解析例题 例1 利用平方差公式计算:
(1) (5+6x)(5?6x);(2) (x+2y)(x?2y); 解: (1) (5+6x)(5?6x)=55第一数a52?要用括号把这个数整个括起来, 再平方; ( )26x=25? 最后的结果又要去掉括号。 36x2 ;(2) (x+2y) (x?2y)
=x2?( )22y=x2 ?4y2 ;练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(m+8)(m-8) 练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(a+8)(a-8) 练习1.运用平方差公式计算:
分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(a+b)(a-b) 练习1.运用平方差公式计算:分析:题目条件是否符合平方差?若能,请找出本题中a和b分别表示什么?
(1)(m+8)(m-8) (2)(2a+5b)(2a-5b) 解:(m+8)(m-8)=
(a+b) (a-b)(2a+5b)(2a-5b)== a2 - b2
(a + b) (a - b)(2a)2-(5b)2=4a2-25b2m2 –82= m2-64= a2 - b2(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。练习2.例2下列各题能否用平方差公式计算,请说明理由,并计算。 (1)(4y+3x)(3x-4y)(加法交换律)解:=(3x+4y)(3x-4y)=(3x)2-(4y)2=9x2-16y2(2)(-4a-b)(4a-b)(加法交换律)解:(-4a-b)(4a-b)
=(-b-4a)(-b+4a)
= (-b)2-(4a)2
= b2-16a2
(-4a-b)(4a-b)(分配律的逆运用)= -(4a+b)(4a-b)= -[(4a)2 -b2]= -(16a2 -b2)= b2 -16a2(3)59.8 × 60.2 解: 59.8 × 60.2(观察数字特点)=(60-0.2)(60+0.2)=602-(0.2)2
=3600-0.04
=3599.96
平方差公式⑷、利用平方差公式计算:1998×2002技巧小结:如何找符合公式(a+b)(a-b)的a和b
把它们的平均数作a,把两数差的一半作b, 平方差公式常用变化形式:①位置变化:②符号变化:③指数变化:④系数变化:⑤数字变化:平方差公式分层练习:A组:判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y) ( )
2、(a-2b)(-a-2b) ( )
3、(-2m-n)(n + 2m) ( )
4、(2c-b)( -b-2c) ( )
B组:1、计算:
(2x+ )(2x- ) (-x+2)(-x-2)
?
(-2x+y)(2x+y) (y-x)(-x-y)
?
2、简便计算:
?(1)498×502 (2)999×1001C组:
1、[(a+b)+(a-b)][(a+b)-(a-b)]
2 、[(a+b)(a-b)] 3、(2x+y+5)(2x+y-5)
思考:(a+b+c)(a-b-c)= ?
4、(x-1)(x2 +1)(x+1)
5、(a-3)(a+4)(a+3)(a-4)
?
6、(2a-5b)(2a+5b)(4a2+25b2)
7、20042-2005×2003平方差公式平方差公式拓展:计算(用指数形式表示)
1、(x-1)(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
?
2、(2+1) (22+1)(24+1) (28+1) (216+1)
?
3、(x+1) (x2+1)(x4+1) (x8+1) (x16+1) 平方差公式常用变化形式:①位置变化:②符号变化:③指数变化:④系数变化:⑤数字变化:⑥增项变化:⑦增因式变化:⑧连用公式变化:平方差公式平方差公式平方差公式的几何背景:请同学们思考如何用几何图形的
面积来解释(a +b)(a-b)呢? 1、当a>b>0时,我们可能看成是以长为(a+b) ,
宽为(a-b)的长方形的面积。 2、如何解释公式的右端:
a2-b2小结试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式; 要利用加法交换律,对于不符合平方差公式标准形式者,
