2.2.1平方差公式 课件 (8)
图片预览






文档简介
课件18张PPT。
2.2.1 《平方差公式》教学设计
在练习本上计算,同桌互相订正:1、(x+2)(x-2) 2、(1+3a)(1-3a)
3、(x+5y)(x-5y) 4、(3a+b)(3a-b)
观察以下算式,你发现了什么规律?再计算:
平方差公式:
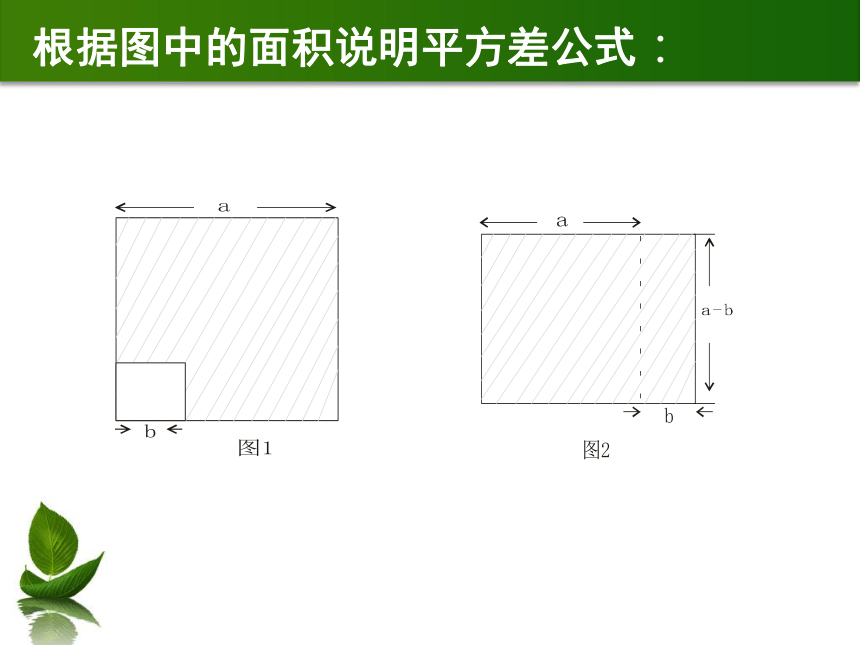
根据图中的面积说明平方差公式:
总结规律:两个数的和与这两个数的差
的积等于这两个数的平方差。
根据图中的面积说明平方差公式:
运用平方差公式计算下面各题:
(2x + 3)(2x–3)
(y + 2x)(2x–y)
(–x + 2y)(–x–2y)
利用平方差公式计算:
总结提示:
首先要看是否符合公式特征,公式中
的字母a、b可以代表具体的数字、字
母、单项式甚至多项式
其次要分清相同项与相反项用今天所学的知识练习:
1002×998
999×1001
49.2×50.2总结:
要运用平方差公式进行简便运
算,就要变为两数之和与这两
数之差的积的形式,关键是要
将某个数拆分成两个相同的数。计算下列各题:
运用公式要注意事项:
(1)要符合公式特征才能运用平方差公式
(2)有些式子表面不能应用公式,
但实质上是能够应用公式的,
要注意变形,归纳容易出错的地方。
总结提示:
①②两小题的解决关键是把两括号内相同的项看
成平方差公式中的a,将相反的项看成公式中的b。
例如:①(a-b+c)(a-b-c)=[(a-b)+c][(a-b)-c]
进一步再用平方差公式。
第④小题恒等变形构成平方差公式,只要在(2+1)
的前面乘以(2-1),第③题逐次用平方差公式
作业:
1、教材第44页的练习。
2、教材第50页习题第一题。
谢谢!
2.2.1 《平方差公式》教学设计
在练习本上计算,同桌互相订正:1、(x+2)(x-2) 2、(1+3a)(1-3a)
3、(x+5y)(x-5y) 4、(3a+b)(3a-b)
观察以下算式,你发现了什么规律?再计算:
平方差公式:
根据图中的面积说明平方差公式:
总结规律:两个数的和与这两个数的差
的积等于这两个数的平方差。
根据图中的面积说明平方差公式:
运用平方差公式计算下面各题:
(2x + 3)(2x–3)
(y + 2x)(2x–y)
(–x + 2y)(–x–2y)
利用平方差公式计算:
总结提示:
首先要看是否符合公式特征,公式中
的字母a、b可以代表具体的数字、字
母、单项式甚至多项式
其次要分清相同项与相反项用今天所学的知识练习:
1002×998
999×1001
49.2×50.2总结:
要运用平方差公式进行简便运
算,就要变为两数之和与这两
数之差的积的形式,关键是要
将某个数拆分成两个相同的数。计算下列各题:
运用公式要注意事项:
(1)要符合公式特征才能运用平方差公式
(2)有些式子表面不能应用公式,
但实质上是能够应用公式的,
要注意变形,归纳容易出错的地方。
总结提示:
①②两小题的解决关键是把两括号内相同的项看
成平方差公式中的a,将相反的项看成公式中的b。
例如:①(a-b+c)(a-b-c)=[(a-b)+c][(a-b)-c]
进一步再用平方差公式。
第④小题恒等变形构成平方差公式,只要在(2+1)
的前面乘以(2-1),第③题逐次用平方差公式
作业:
1、教材第44页的练习。
2、教材第50页习题第一题。
谢谢!
