2.2.2 完全平方公式 课件 (4)
文档属性
| 名称 | 2.2.2 完全平方公式 课件 (4) |

|
|
| 格式 | ppt | ||
| 文件大小 | 487.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-10 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
怎样快速地计算(2x+y)2呢?
计算下列各式,你发现什么规律?
(a+1)2=(a+1)(a+1)=a2+a+a+1=a2+2·a·1+12,
(a+2)2= = =a2+ +22,
(a-1)2= = =a2- +12,
(a+b)2= = =a2+ +b2,
(a-b)2= = =a2- +b2,
(a+2)(a+2)
a2+2a+2a+4
2·a·2
(a-b)(a-b)
(a-1)(a-1)
a2-ab-ab+b2
a2-a-a+1
2·a·b
2·a·1
(a+b)(a-b)
a2+ab+ab+b2
2·a·b
(2x+y)2=(2x)2+2·2x·y+y2
比较(a + b)2= a2 +2· a· b+b2
完全平方公式:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
完全平方公式的意义是:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的两倍。
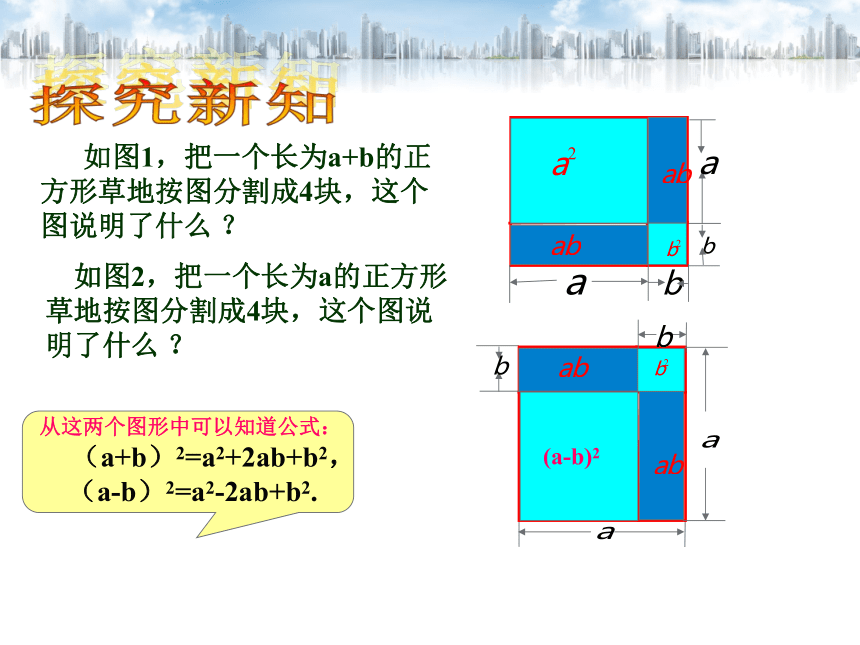
如图1,把一个长为a+b的正方形草地按图分割成4块,这个图说明了什么 ?
(a-b)2
从这两个图形中可以知道公式:
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
如图2,把一个长为a的正方形草地按图分割成4块,这个图说明了什么 ?
解:(1)(3m+n)2 =(3m)2+2·3m·n+n2=9m2+6mn+n2
(2)(x- )2=x2-2·x· + ( ) 2=x2-x+
例1、运用完全平方公式计算:
(1)(3m+n)2 (2)(x- )2
例2、运用完全平方公式计算:
(1)(-x+1)2 (2)(-2x- 3 )2
解:(1)(-x+1)2=(-x)2+2·(-x)·1+12=x2-2x+1
(2) (-2x- 3)2=(-2x)2-2·(-2x)·3+32=4x2+12x+9
怎样快速地计算(2x+y)2呢?
计算下列各式,你发现什么规律?
(a+1)2=(a+1)(a+1)=a2+a+a+1=a2+2·a·1+12,
(a+2)2= = =a2+ +22,
(a-1)2= = =a2- +12,
(a+b)2= = =a2+ +b2,
(a-b)2= = =a2- +b2,
(a+2)(a+2)
a2+2a+2a+4
2·a·2
(a-b)(a-b)
(a-1)(a-1)
a2-ab-ab+b2
a2-a-a+1
2·a·b
2·a·1
(a+b)(a-b)
a2+ab+ab+b2
2·a·b
(2x+y)2=(2x)2+2·2x·y+y2
比较(a + b)2= a2 +2· a· b+b2
完全平方公式:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
完全平方公式的意义是:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的两倍。
如图1,把一个长为a+b的正方形草地按图分割成4块,这个图说明了什么 ?
(a-b)2
从这两个图形中可以知道公式:
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
如图2,把一个长为a的正方形草地按图分割成4块,这个图说明了什么 ?
解:(1)(3m+n)2 =(3m)2+2·3m·n+n2=9m2+6mn+n2
(2)(x- )2=x2-2·x· + ( ) 2=x2-x+
例1、运用完全平方公式计算:
(1)(3m+n)2 (2)(x- )2
例2、运用完全平方公式计算:
(1)(-x+1)2 (2)(-2x- 3 )2
解:(1)(-x+1)2=(-x)2+2·(-x)·1+12=x2-2x+1
(2) (-2x- 3)2=(-2x)2-2·(-2x)·3+32=4x2+12x+9
