4.1.1相交与平行 课件 (5)
图片预览










文档简介
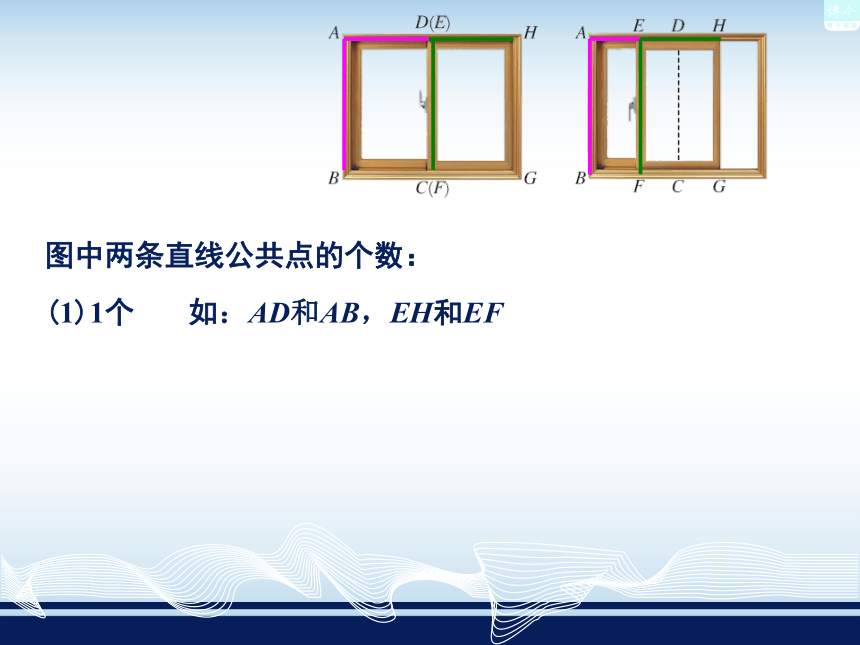
课件30张PPT。相交与平行第4章 平面上两条直线的位置关系4.1平面上两条直线的位置关系(链接)平行线的画法(链接)平行公理及推论(链接)4.1.1相交与平行返回(一)平面上两条直线的位置关系返回 小明家客厅的窗户由两扇塑钢玻璃窗页组成,下图为两扇窗页全关、半开的状态. 我们把两扇窗页近似地看成在同一平面内,观察图中每扇窗页的塑钢边所在的直线.问题1:
①图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.图中两条直线公共点的个数:
(1)1个如:AD和AB,EH和EF图中两条直线公共点的个数:
(1)1个
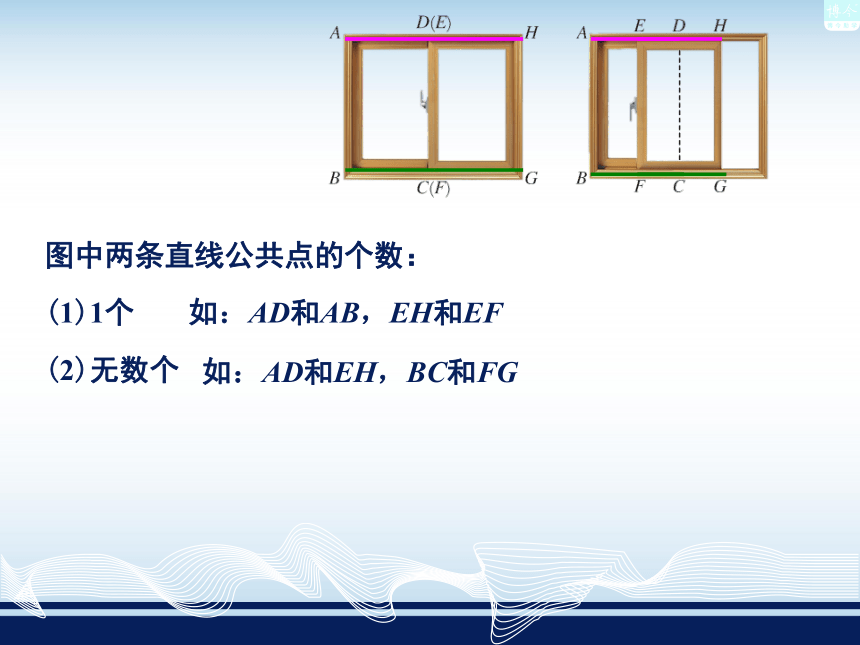
(2)无数个如:AD和AB,EH和EF如:AD和EH,BC和FG如:AB和DC,AD和BC图中两条直线公共点的个数:
(1)1个
(2)无数个
(3)0个如:AD和AB,EH和EF如:AD和EH,BC和FG 小明家客厅的窗户由两扇塑钢玻璃窗页组成,下图为两扇窗页全关、半开的状态. 我们把两扇窗页近似地看成在同一平面内,观察图中每扇窗页的塑钢边所在的直线.问题1:
②这些直线的相互位置有哪些关系?图3-36如:AB和DC,AD和BC图中两条直线公共点的个数:
(1)1个
(2)无数个
(3)0个如:AD和AB,EH和EF如:AD和EH,BC和FG相交重合既不相交,也不重合 由此可见,同一平面上的两条直线,可能相交,可能重合,还可能既不相交,也不重合. 今后如果没有特别说明,两条重合的直线只当做一条. 铁路上的两条铁轨,一排挺立的电杆,栅栏里的竖条,都给我们以两条直线既不重合也不相交的形象.这样的两条直线没有公共点. 同一平面内没有公共点的两条直线叫做平行线. 平行用符号“∥”表示. 若AB与CD平行,记做AB ∥ CD,读做AB平行于CD. 问题2:平行线在生活中很常见, 你能举出一些例子吗? 双杠、梯子、操场上的跑道.问题3:在同一平面内,两条直线有哪些位置关系?相交和平行(二)平行线的画法返回问题4:如何画平行线呢?给一条直线a,你能画出直线a的平行线吗?(三)平行公理及其推论返回问题5:过点B画直线a的平行线,能画出几条?再过点C画直线c的平行线,它和前面过点B画出的直线平行吗?平行公理: 经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:平行于同一直线的两条直线平行.如果a∥b,c∥b,那么a∥c. ???? 这是因为,若a与c不平行,就会相交于某一点P,那么过点P就有两条直线与b平行,这是不可能的,
所以a∥c. 一条线段向两端无限延伸就得到一条直线,这说明直线有两个方向,取定一个方向,就确定了另一个方向.问题6: 在每条直线上取定一个方向,两条直线平行,它们的方向有什么关系?若两条直线平行, 则它们的方向相同或相反,问题7: 具有相同方向或相反方向的两条直线有什么位置关系?两条直线平行两条直线平行 两条直线的方向相同或相反 1. 读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.(1)(2).PEFDC2. 如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?答:假设EF∥CD,
则因AB∥CD,
所以根据平行线的传递性,
便有AB∥EF.
与AB和EF相交于P点矛盾,
所以EF与CD不平行.3. 如图是用电脑画出来的“花”,它由一些平行线段组成,先指出其中有几组平行线段,然后自己也用画平行线的方法设计一件“艺术品”. 例1 如图,在长方体中,与棱AD平行的棱共有 条.3 1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么? 结 束
①图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.图中两条直线公共点的个数:
(1)1个如:AD和AB,EH和EF图中两条直线公共点的个数:
(1)1个
(2)无数个如:AD和AB,EH和EF如:AD和EH,BC和FG如:AB和DC,AD和BC图中两条直线公共点的个数:
(1)1个
(2)无数个
(3)0个如:AD和AB,EH和EF如:AD和EH,BC和FG 小明家客厅的窗户由两扇塑钢玻璃窗页组成,下图为两扇窗页全关、半开的状态. 我们把两扇窗页近似地看成在同一平面内,观察图中每扇窗页的塑钢边所在的直线.问题1:
②这些直线的相互位置有哪些关系?图3-36如:AB和DC,AD和BC图中两条直线公共点的个数:
(1)1个
(2)无数个
(3)0个如:AD和AB,EH和EF如:AD和EH,BC和FG相交重合既不相交,也不重合 由此可见,同一平面上的两条直线,可能相交,可能重合,还可能既不相交,也不重合. 今后如果没有特别说明,两条重合的直线只当做一条. 铁路上的两条铁轨,一排挺立的电杆,栅栏里的竖条,都给我们以两条直线既不重合也不相交的形象.这样的两条直线没有公共点. 同一平面内没有公共点的两条直线叫做平行线. 平行用符号“∥”表示. 若AB与CD平行,记做AB ∥ CD,读做AB平行于CD. 问题2:平行线在生活中很常见, 你能举出一些例子吗? 双杠、梯子、操场上的跑道.问题3:在同一平面内,两条直线有哪些位置关系?相交和平行(二)平行线的画法返回问题4:如何画平行线呢?给一条直线a,你能画出直线a的平行线吗?(三)平行公理及其推论返回问题5:过点B画直线a的平行线,能画出几条?再过点C画直线c的平行线,它和前面过点B画出的直线平行吗?平行公理: 经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:平行于同一直线的两条直线平行.如果a∥b,c∥b,那么a∥c. ???? 这是因为,若a与c不平行,就会相交于某一点P,那么过点P就有两条直线与b平行,这是不可能的,
所以a∥c. 一条线段向两端无限延伸就得到一条直线,这说明直线有两个方向,取定一个方向,就确定了另一个方向.问题6: 在每条直线上取定一个方向,两条直线平行,它们的方向有什么关系?若两条直线平行, 则它们的方向相同或相反,问题7: 具有相同方向或相反方向的两条直线有什么位置关系?两条直线平行两条直线平行 两条直线的方向相同或相反 1. 读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.(1)(2).PEFDC2. 如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?答:假设EF∥CD,
则因AB∥CD,
所以根据平行线的传递性,
便有AB∥EF.
与AB和EF相交于P点矛盾,
所以EF与CD不平行.3. 如图是用电脑画出来的“花”,它由一些平行线段组成,先指出其中有几组平行线段,然后自己也用画平行线的方法设计一件“艺术品”. 例1 如图,在长方体中,与棱AD平行的棱共有 条.3 1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么? 结 束
