5.1.2 轴对称变换 课件 (4)
图片预览








文档简介
(共25张PPT)
建筑物中轴对称图形
图 片 欣 赏
蝴 蝶
秋天落叶
蜻 蜓
大自然中的轴对称图形
图 片 欣 赏
民间剪纸艺术
知识回顾:什么是轴对称图形?
轴对称图形有什么性质
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
学习目标
1、了解轴对称、轴对称变换、像 的概念;
2、掌握轴对称变换的性质,会应用性质作某图形经轴对称变换后的像。
自学指导
请同学们认真阅读课本P115-117,思考:
(1)什么是轴对称变换?
(2)轴对称变换和轴对称图形有什么不同点和相同点?
把图形(a)沿着直线 l 翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l 作了轴对称变换, 也叫轴反射.
l
P
P’
原像
像
对称轴
(a)
(b)
图形(a)叫做原像
图形(b)叫做图形(a)
在这个轴反射下的像。
①
②
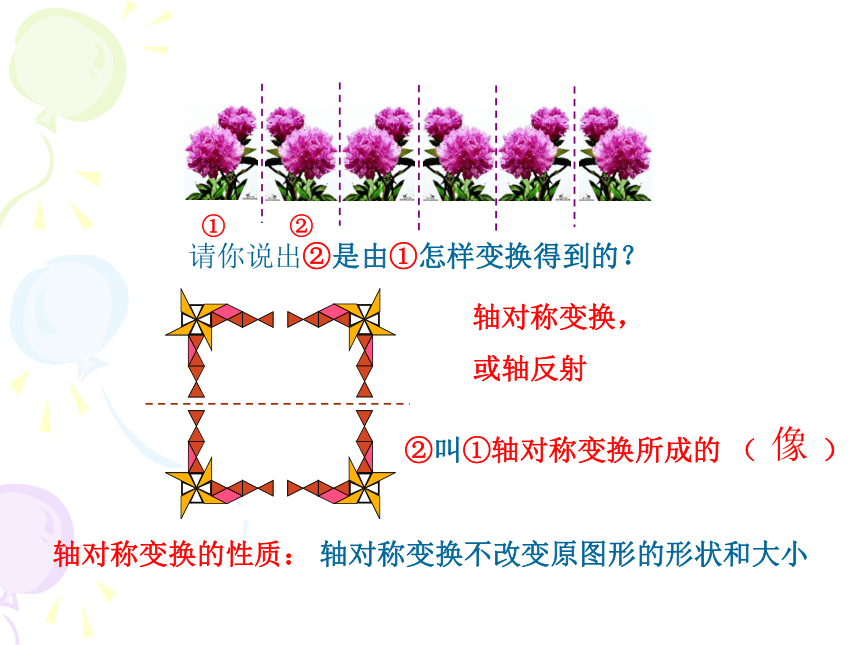
请你说出②是由①怎样变换得到的?
②叫①轴对称变换所成的 ( )
像
轴对称变换,
或轴反射
轴对称变换的性质: 轴对称变换不改变原图形的形状和大小
看成两个图形
两个图形成轴对称
相同点:都是沿一条直线折叠后能够互相重合。
轴对称变换和轴对称图形有什么不同点和相同点?
不同点:轴对称图形是一个图形。
轴对称变换是两个图形之间的关系。
大自然中的轴对称变换
世界著名建筑
作点A关于直线 的对称点
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
1、过点A作直线 的垂线,垂足为O
O
第一关
2、在射线AO上取一点 ,使
=
点 为所求的点
已知对称轴 和线段AB,画出线段AB经轴对称变换后所得的像A′B′。
A'
B'
A
B
B'
B
A
A'
注:对称轴上的点的像是它本身
B
A
B‘
A’
第二关
成轴对称的两个图形中,对应点的连线被对称轴垂直平分
轴对称变换的性质:
M
1、过点A作直线l的垂线,垂足为点O,
在垂线上截取OA’=OA,
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求。
A’
B’
C’
O
点A’就是点A关于直线l的对称点;
作已知图形关于已知直线对称的图形的一般步聚
1、确定关键点
2、一一做出关键点的对称点
3、连线
X
A、
B、
C、
D、
D
如图,已知图形X和直线 。将图形X以直线 为对称轴,作轴对称变换后得到的图形是( )。
实际图形与它在镜子里的像构成轴对称关系。
印章上的
“马”
刻在印章上的 字与印在纸上的 字,把它们并排放在一起,它们成轴对称。
“马”
“马”
印在纸上的
“马”
轴对称变换后的像
原来的图形
猜单词游戏
1、
6、
5、
3、
2、
4、
轴对称变换后的像
原来的图形
小结:
把图形沿着直线翻折并将图形“复印”,下来得到的图形,就叫做该图形关于直线作了轴对称变换, 也叫轴反射.经变换所得的新图形叫原图形的像.
轴对称变换及相关概念:
轴对称变换的性质:
轴对称变换不改变原图形的形状和大小。
轴对称图形和轴对称
变换的区别和联系:
由一个图形变为另一个图形的这种改变的
过程是轴对称变换,而变换后的结果看成
一个图形时是轴对称图形。
成轴对称的两个图形中,对应点的连线被对称轴垂直平分
作已知图形关于已知直线对称的图形的一般步聚
(1)确定关键点
(2)一一做出关键点的对称点
(3)连线
将一张纸对折后,用笔尖在纸上扎出你喜欢的图案(例如图).将纸打开后铺平,观察所得到的图案.
你得到的图案有什么特征?
位于折痕两侧的部分有什么关系?
与同伴进行交流.
课外作业
建筑物中轴对称图形
图 片 欣 赏
蝴 蝶
秋天落叶
蜻 蜓
大自然中的轴对称图形
图 片 欣 赏
民间剪纸艺术
知识回顾:什么是轴对称图形?
轴对称图形有什么性质
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
学习目标
1、了解轴对称、轴对称变换、像 的概念;
2、掌握轴对称变换的性质,会应用性质作某图形经轴对称变换后的像。
自学指导
请同学们认真阅读课本P115-117,思考:
(1)什么是轴对称变换?
(2)轴对称变换和轴对称图形有什么不同点和相同点?
把图形(a)沿着直线 l 翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l 作了轴对称变换, 也叫轴反射.
l
P
P’
原像
像
对称轴
(a)
(b)
图形(a)叫做原像
图形(b)叫做图形(a)
在这个轴反射下的像。
①
②
请你说出②是由①怎样变换得到的?
②叫①轴对称变换所成的 ( )
像
轴对称变换,
或轴反射
轴对称变换的性质: 轴对称变换不改变原图形的形状和大小
看成两个图形
两个图形成轴对称
相同点:都是沿一条直线折叠后能够互相重合。
轴对称变换和轴对称图形有什么不同点和相同点?
不同点:轴对称图形是一个图形。
轴对称变换是两个图形之间的关系。
大自然中的轴对称变换
世界著名建筑
作点A关于直线 的对称点
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
1、过点A作直线 的垂线,垂足为O
O
第一关
2、在射线AO上取一点 ,使
=
点 为所求的点
已知对称轴 和线段AB,画出线段AB经轴对称变换后所得的像A′B′。
A'
B'
A
B
B'
B
A
A'
注:对称轴上的点的像是它本身
B
A
B‘
A’
第二关
成轴对称的两个图形中,对应点的连线被对称轴垂直平分
轴对称变换的性质:
M
1、过点A作直线l的垂线,垂足为点O,
在垂线上截取OA’=OA,
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求。
A’
B’
C’
O
点A’就是点A关于直线l的对称点;
作已知图形关于已知直线对称的图形的一般步聚
1、确定关键点
2、一一做出关键点的对称点
3、连线
X
A、
B、
C、
D、
D
如图,已知图形X和直线 。将图形X以直线 为对称轴,作轴对称变换后得到的图形是( )。
实际图形与它在镜子里的像构成轴对称关系。
印章上的
“马”
刻在印章上的 字与印在纸上的 字,把它们并排放在一起,它们成轴对称。
“马”
“马”
印在纸上的
“马”
轴对称变换后的像
原来的图形
猜单词游戏
1、
6、
5、
3、
2、
4、
轴对称变换后的像
原来的图形
小结:
把图形沿着直线翻折并将图形“复印”,下来得到的图形,就叫做该图形关于直线作了轴对称变换, 也叫轴反射.经变换所得的新图形叫原图形的像.
轴对称变换及相关概念:
轴对称变换的性质:
轴对称变换不改变原图形的形状和大小。
轴对称图形和轴对称
变换的区别和联系:
由一个图形变为另一个图形的这种改变的
过程是轴对称变换,而变换后的结果看成
一个图形时是轴对称图形。
成轴对称的两个图形中,对应点的连线被对称轴垂直平分
作已知图形关于已知直线对称的图形的一般步聚
(1)确定关键点
(2)一一做出关键点的对称点
(3)连线
将一张纸对折后,用笔尖在纸上扎出你喜欢的图案(例如图).将纸打开后铺平,观察所得到的图案.
你得到的图案有什么特征?
位于折痕两侧的部分有什么关系?
与同伴进行交流.
课外作业
