3.3 中心对称 同步练习(含解析)2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 3.3 中心对称 同步练习(含解析)2024-2025学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 16:34:39 | ||
图片预览

文档简介
3.3中心对称
刷基础
知识点1 中心对称的定义及性质
1[2024 湖北十堰期末]下列四组图形中,左边的图形与右边的图形成中心对称的有 ( )
A.1组 B.2组 C.3组 D.4组
2[2023 宁夏银川期末]如图,△ABC与△A'B'C'关于点O 成中心对称,下列结论中不成立的是( )
A. OB=OB' B.∠ACB=∠A'B'C'
C.点A 的对称点是点A' D. BC∥B'C'
3如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A 的对应点是点A',AB⊥a于点B,A'D⊥b于点 D.若OB=4,OD=3,则阴影部分的面积之和为 .
如图,△ABO 与△CDO 关于O 点成中心对称,点 E,F 在线段 AC 上,且 AF = CE,求证:FD=BE.
知识点2 中心对称作图
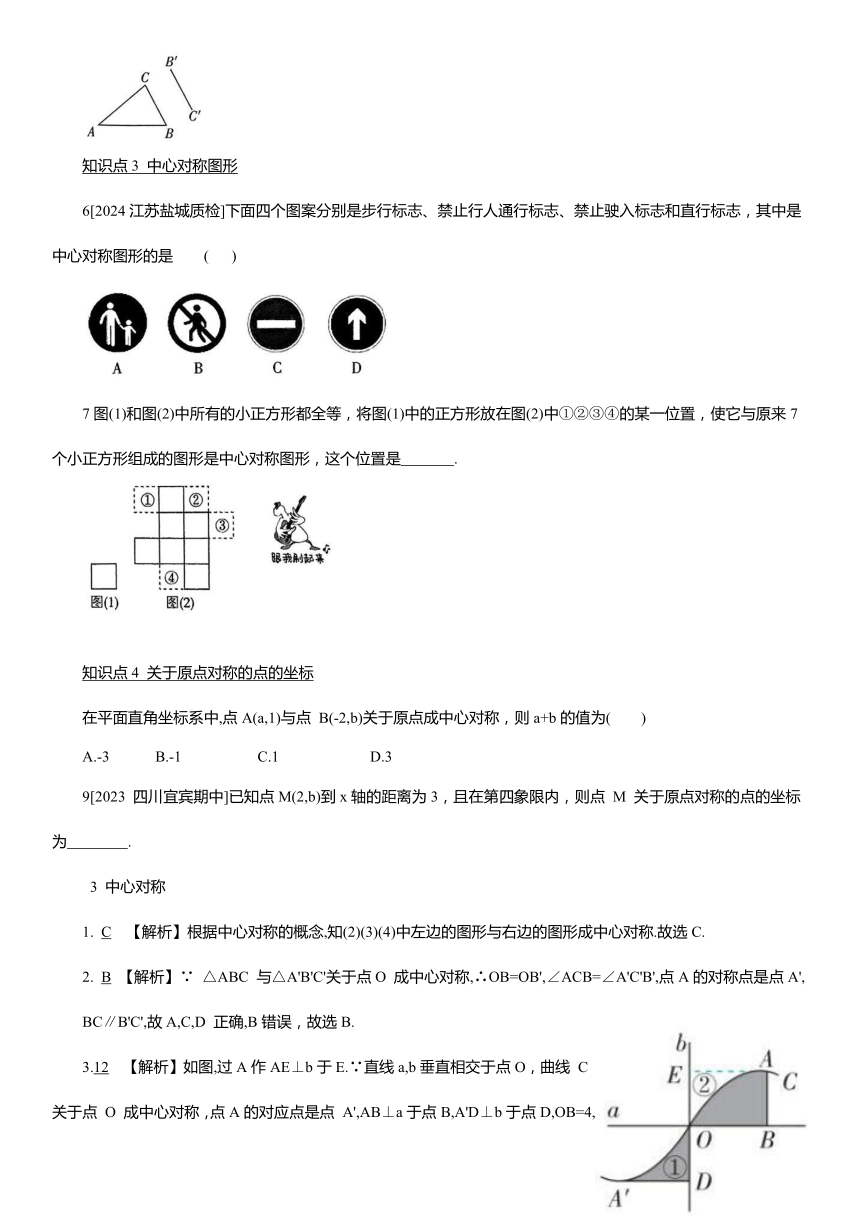
5[2023 河北邢台期末]如图,△ABC 和△A'B'C'关于某一点成中心对称,一同学不小心把墨水泼在纸上,只能看到△ABC 和线段 BC 的对应线段B'C',请你帮该同学找到对称中心O,并补全△A'B'C'.
知识点3 中心对称图形
6[2024江苏盐城质检]下面四个图案分别是步行标志、禁止行人通行标志、禁止驶入标志和直行标志,其中是中心对称图形的是 ( )
7图(1)和图(2)中所有的小正方形都全等,将图(1)中的正方形放在图(2)中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
知识点4 关于原点对称的点的坐标
在平面直角坐标系中,点A(a,1)与点 B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
9[2023 四川宜宾期中]已知点M(2,b)到x轴的距离为3,且在第四象限内,则点 M 关于原点对称的点的坐标为 .
3 中心对称
C 【解析】根据中心对称的概念,知(2)(3)(4)中左边的图形与右边的图形成中心对称.故选C.
2. B 【解析】∵ △ABC 与△A'B'C'关于点O 成中心对称,∴OB=OB',∠ACB=∠A'C'B',点A的对称点是点A',BC∥B'C',故A,C,D 正确,B错误,故选B.
3.12 【解析】如图,过A作AE⊥b于E.∵直线a,b垂直相交于点O,曲线 C 关于点 O 成中心对称,点A的对应点是点 A',AB⊥a于点B,A'D⊥b于点D,OB=4,OD=3,∴OE=OD=3,图形①与图形②面积相等,∴阴影部分的面积之和等于长方形ABOE 的面积,即3×4=12.故答案为12.
4.【证明】∵ △ABO 与△CDO 关于O 点成中心对称,∴BO=DO,AO=CO.
在 和 中
5.【解】如图,点O 为对称中心,. 即为所作.
6. C 【解析】A选项中的图形不是中心对称图形;B选项中的图形不是中心对称图形;C选项中的图形是中心对称图形;D选项中的图形不是中心对称图形.故选 C.
7.③ 【解析】当题图(1)中的正方形放在题图(2)中③的位置,可使组成的图形是中心对称图形.故答案为③.
8. C 【解析】∵点A(a,1)与点 关于原点成中心对称,. 故选 C.
【解析】∵点M(2,b)到x轴的距离为3,且在第四象限内,. ∴点M 关于原点对称的点的坐标为( 故答案为(
刷提升
1. A 【解析】A选项,既是轴对称图形,又是中心对称图形,符合题意;B选项,是中心对称图形,不是轴对称图形,不符合题意;C选项,是中心对称图形,不是轴对称图形,不符合题意;D选项,是中心对称图形,不是轴对称图形,不符合题意.故选A.
2. A 【解析】∵点B,C的坐标分别为(2,1), 是等腰直角三角形,∴A(4,3).设直线AB 的表达式为 则 解得 ∴直线AB 的表达式为 令 则 又∵点A与点. 关于点P成中心对称,∴点 P 为. 的中点.设. n),则 故选A.
3.(2,1) 【解析】由题图可知 成中心对称的两个图形中,对应点的连线都经过对称中心,并且被对称中心平分,∴对称中心的坐标为 即(2,1).
4.2023 【解析】如图,在图中用字母标出部分点,作 于E, 交MH延长线于F, 则易得
在 和 中,
同理,各个重合部分的面积都是1,则n个这样的正方形重叠部分(阴影部分)的面积和为 1)=n-1,∴2024个这样的正方形重叠部分(阴影部分)的面积和为 故答案为2023.
5.【解】(1)根据题意得,点A 与点 P,点B 与点Q,点C 与点 R 关于原点 O 成中心对称,
与 关于原点O 成中心对称,
∴点M与点 N关于原点O 成中心对称,
∴点N的坐标为(
故答案为(
(2)如图, 即为所求.
(3)设直线AC 表达式为 把A(4,3),C(1,2)代入,得 解得 直线AC 表达式为 当 时, 即直线AC 与y轴交点的坐标为 故答案为
刷素养
6.【解】(1)由题意得,直线 EF 经过四边形ABCD的对称中心O,则S四边形AEFB=S四边形DEFC·故答案为=.
(2)如图(1),直线l即为所作.
(3)如图(2),直线a,b,c即为所作.
刷基础
知识点1 中心对称的定义及性质
1[2024 湖北十堰期末]下列四组图形中,左边的图形与右边的图形成中心对称的有 ( )
A.1组 B.2组 C.3组 D.4组
2[2023 宁夏银川期末]如图,△ABC与△A'B'C'关于点O 成中心对称,下列结论中不成立的是( )
A. OB=OB' B.∠ACB=∠A'B'C'
C.点A 的对称点是点A' D. BC∥B'C'
3如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A 的对应点是点A',AB⊥a于点B,A'D⊥b于点 D.若OB=4,OD=3,则阴影部分的面积之和为 .
如图,△ABO 与△CDO 关于O 点成中心对称,点 E,F 在线段 AC 上,且 AF = CE,求证:FD=BE.
知识点2 中心对称作图
5[2023 河北邢台期末]如图,△ABC 和△A'B'C'关于某一点成中心对称,一同学不小心把墨水泼在纸上,只能看到△ABC 和线段 BC 的对应线段B'C',请你帮该同学找到对称中心O,并补全△A'B'C'.
知识点3 中心对称图形
6[2024江苏盐城质检]下面四个图案分别是步行标志、禁止行人通行标志、禁止驶入标志和直行标志,其中是中心对称图形的是 ( )
7图(1)和图(2)中所有的小正方形都全等,将图(1)中的正方形放在图(2)中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 .
知识点4 关于原点对称的点的坐标
在平面直角坐标系中,点A(a,1)与点 B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
9[2023 四川宜宾期中]已知点M(2,b)到x轴的距离为3,且在第四象限内,则点 M 关于原点对称的点的坐标为 .
3 中心对称
C 【解析】根据中心对称的概念,知(2)(3)(4)中左边的图形与右边的图形成中心对称.故选C.
2. B 【解析】∵ △ABC 与△A'B'C'关于点O 成中心对称,∴OB=OB',∠ACB=∠A'C'B',点A的对称点是点A',BC∥B'C',故A,C,D 正确,B错误,故选B.
3.12 【解析】如图,过A作AE⊥b于E.∵直线a,b垂直相交于点O,曲线 C 关于点 O 成中心对称,点A的对应点是点 A',AB⊥a于点B,A'D⊥b于点D,OB=4,OD=3,∴OE=OD=3,图形①与图形②面积相等,∴阴影部分的面积之和等于长方形ABOE 的面积,即3×4=12.故答案为12.
4.【证明】∵ △ABO 与△CDO 关于O 点成中心对称,∴BO=DO,AO=CO.
在 和 中
5.【解】如图,点O 为对称中心,. 即为所作.
6. C 【解析】A选项中的图形不是中心对称图形;B选项中的图形不是中心对称图形;C选项中的图形是中心对称图形;D选项中的图形不是中心对称图形.故选 C.
7.③ 【解析】当题图(1)中的正方形放在题图(2)中③的位置,可使组成的图形是中心对称图形.故答案为③.
8. C 【解析】∵点A(a,1)与点 关于原点成中心对称,. 故选 C.
【解析】∵点M(2,b)到x轴的距离为3,且在第四象限内,. ∴点M 关于原点对称的点的坐标为( 故答案为(
刷提升
1. A 【解析】A选项,既是轴对称图形,又是中心对称图形,符合题意;B选项,是中心对称图形,不是轴对称图形,不符合题意;C选项,是中心对称图形,不是轴对称图形,不符合题意;D选项,是中心对称图形,不是轴对称图形,不符合题意.故选A.
2. A 【解析】∵点B,C的坐标分别为(2,1), 是等腰直角三角形,∴A(4,3).设直线AB 的表达式为 则 解得 ∴直线AB 的表达式为 令 则 又∵点A与点. 关于点P成中心对称,∴点 P 为. 的中点.设. n),则 故选A.
3.(2,1) 【解析】由题图可知 成中心对称的两个图形中,对应点的连线都经过对称中心,并且被对称中心平分,∴对称中心的坐标为 即(2,1).
4.2023 【解析】如图,在图中用字母标出部分点,作 于E, 交MH延长线于F, 则易得
在 和 中,
同理,各个重合部分的面积都是1,则n个这样的正方形重叠部分(阴影部分)的面积和为 1)=n-1,∴2024个这样的正方形重叠部分(阴影部分)的面积和为 故答案为2023.
5.【解】(1)根据题意得,点A 与点 P,点B 与点Q,点C 与点 R 关于原点 O 成中心对称,
与 关于原点O 成中心对称,
∴点M与点 N关于原点O 成中心对称,
∴点N的坐标为(
故答案为(
(2)如图, 即为所求.
(3)设直线AC 表达式为 把A(4,3),C(1,2)代入,得 解得 直线AC 表达式为 当 时, 即直线AC 与y轴交点的坐标为 故答案为
刷素养
6.【解】(1)由题意得,直线 EF 经过四边形ABCD的对称中心O,则S四边形AEFB=S四边形DEFC·故答案为=.
(2)如图(1),直线l即为所作.
(3)如图(2),直线a,b,c即为所作.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
