第三章 图形的平移与旋转 专题5 旋转中的全等模型 同步练习(含答案)2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 第三章 图形的平移与旋转 专题5 旋转中的全等模型 同步练习(含答案)2024-2025学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 145.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 16:38:32 | ||
图片预览



文档简介
专题5 旋转中的全等模型
母题学大招9手拉手模型
1[2024 浙江杭州期末,中]图(1)是边长分别为a和b(a>b)的两个等边三角形纸片 ABC 和 C'DE 叠放在一起(C与C'重合)组成的图形.
(1)操作:固定△ABC,将△C'DE 绕点 C 按顺时针方向旋转20°,连接AD,BE,如图(2),线段BE 与AD 之间具有怎样的数量关系 证明你的结论.
(2)操作:若将图(1)中的△C'DE,绕点 C 按顺时针方向任意旋转一个角度α,连接AD,BE,如图(3),线段BE与AD 之间是否仍符合(1)中的结论 若是,请证明;若不是,请直接写出BE与AD之间的数量关系.
(3)根据上面的操作过程,请问当α为多少度时 线段AD 的长度最大 最大值是多少 当α为多少度时,线段AD 的长度最小 最小值是多少
子题练变式
2[2024 浙江宁波校级期末,中]【基础巩固】(1)如图(1),在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△AEC≌△ADB.
【尝试应用】(2)如图(2),在△ABC 与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B,D,E三点在一条直线上,AC与BE 交于点 F,若点F为AC中点,
①求∠BEC 的大小;
②若CE=2,求△ACE的面积.
母题学大招10 半角模型
3[2024上海闵行区质检,中]如图,正方形ABCD中,E,F分别在边BC,CD上,且∠EAF=45°,连接 EF,这种模型属于“半角模型”中的一类.在解决“半角模型”问题时,旋转是一种常用的解题方法.例如将△ADF绕点A 顺时针旋转90°得到△ABG,则可以证明“EF=BE+DF”,请写出证明过程.
子题练变式 含60°的半角模型
4[2024 江苏南京质检,中]已知四边形 ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕 B 点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
(1)当∠MBN 绕 B 点旋转到 AE =CF 时(如图(1)),AE,CF,EF 之间的数量关系为
(2)当 E 在AD 上,F 在 DC上,但AE≠CF 时(如图(2)),(1)中结论是否成立 请说明理由.
(3)当 E在AD 延长线上,F在DC延长线上时(如图(3)),(1)中结论是否成立 若不成立,线段AE,CF,EF之间又有怎样的数量关系 请直接写出你的猜想.
母题学大招11 费马点模型
5[2024江苏扬州期末,较难]背景资料:
在已知△ABC 所在平面上求一点 P,使它到三角形的三个顶点的距离之和最小.
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”,
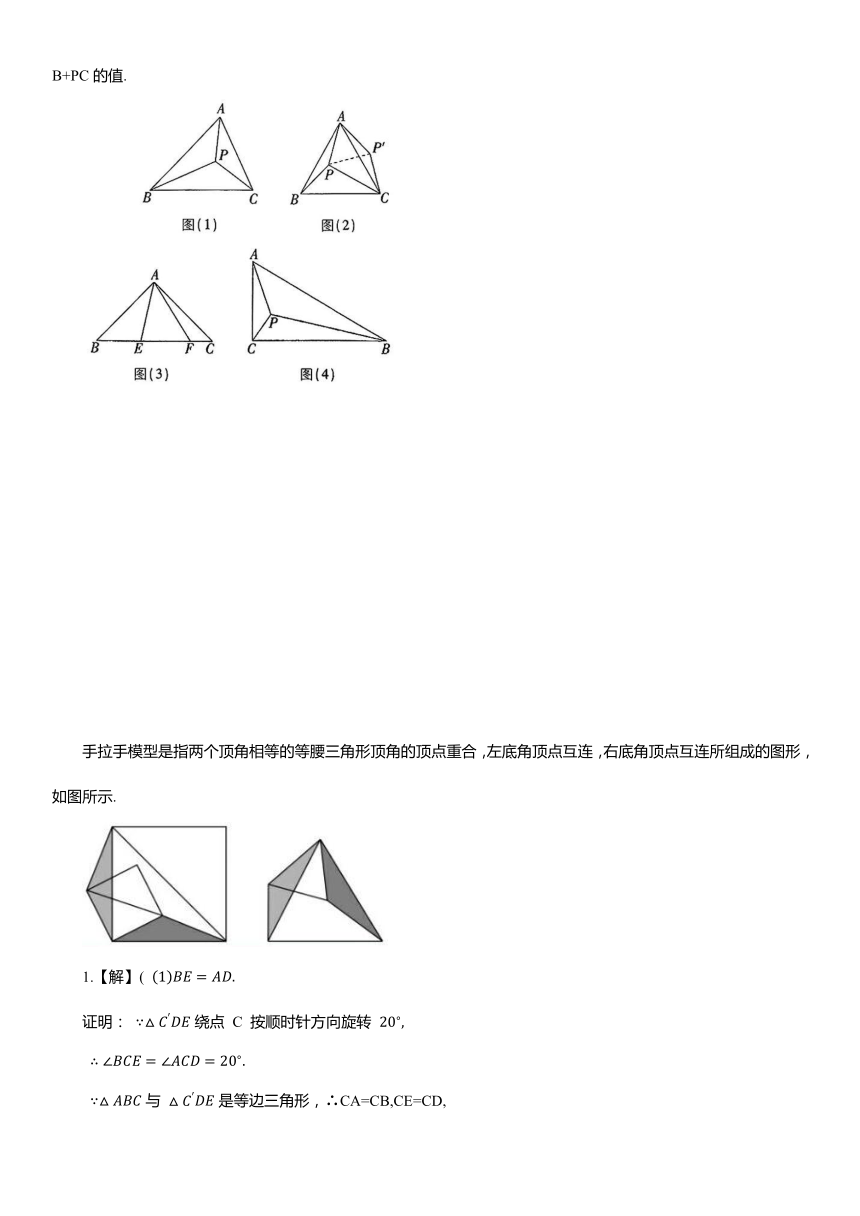
如图(1),当△ABC三个内角均小于120°时,费马点 P 在△ABC 内部,此时∠APB=∠BPC=∠CPA=120°,此时,PA+PB+PC的值最小.
解决问题:
(1)如图(2),等边△ABC 内有一点 P,若点 P到顶点A,B,C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP 绕顶点A旋转到△ACP'处,此时△ACP'≌△ABP,这样就可以利用旋转变换,将三条线段 PA,PB,PC转化到一个三角形中,从而求出∠APB= ;基本运用:
(2)请你利用第(1)题的解答思想方法,解答下面问题:
如图(3),△ABC中,∠CAB=90°,AB=AC,E,F为BC上的点,且∠EAF=45°,判断BE,EF,FC之间的数量关系并证明;
能力提升:
(3)如图(4),在 Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,点 P 为 Rt△ABC 的费马点,连接AP,BP,CP,求PA+PB+PC的值.
手拉手模型是指两个顶角相等的等腰三角形顶角的顶点重合,左底角顶点互连,右底角顶点互连所组成的图形,如图所示.
1.【解】(
证明: 绕点 C 按顺时针方向旋转
与 是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
(2)是.
证明:∵△C'DE 绕点 C 按顺时针方向旋转的角度为α,
∴∠BCE=∠ACD=α.
∵△ABC 与△C'DE是等边三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD.
(3)当点 D 旋转到 CA 的反向延长线上,即α=180°时,线段AD的长度最大,最大值为a+
b.当点 D 在AC边上,即α=0°时,线段AD的长度最小,最小值为a-b.
2.(1)【证明】∵ ∠BAC=∠DAE,∴ ∠BAC-∠BAE=∠DAE-∠BAE,即∠CAE=∠BAD.
在△AEC 和△ADB中,
∴△AEC≌△ADB(SAS).
【解】(2) ①∵ AD = AE, ∠DAE = 90°,∴ ∠ADE=∠AED = 45°,∴ ∠ADB = 180°-∠ADE=180°-45°=135°,同(1)得△AEC≌△ADB(SAS),∴ ∠AEC = ∠ADB = 135°,∴ ∠BEC=∠AEC-∠AED=135°-45°=90°.
②如图,过点 A 作AG⊥DE于点 G, 则 ∠FGA = 90°,由①可知, ∠FEC = 90°,∴ ∠FGA =∠FEC.∵点F为 AC 中点,∴ AF = CF.又 易得
大招解读|半角模型
半角模型特征:①共端点的等线段;②共顶点的倍半角.通过旋转或作辅助线可以构造全等三角形.常见的半角模型有 角含 角和 角含 角.半角模型在实际应用中会证两次全等,如图, 和
3.【解】∵ 四边形ABCD为正方形,∴AB=AD,∠ADF=∠ABE=90°.∵△ADF 绕点 A 顺时针旋转 90°得到 △ABG,∴ △ADF≌ △ABG,∴AF=AG,BG=DF,∠DAF=∠GAB,∠ABG=∠ADF=90°,∴∠ABG+∠ABC=180°,∴G,B,E共线. ∵∠EAF=45°, ∴∠DAF+∠EAB =45°,∴∠GAB+∠EAB=45°,∴∠GAE=∠EAF=
45°. 在 △AGE 和 △AFE 中,
∴△AGE≌△AFE(SAS),∴GE=EF,∴EF=GE=BE+GB=BE+DF.
4.【解】(1)∵AB⊥AD,BC⊥CD,∴∠A=∠C=90°.∵AB=BC,AE=CF,∴ △ABE≌△CBF(SAS),∴ ∠ABE=∠CBF,BE=BF.∵ ∠ABC= BF,∴△BEF是等边三角形, 故答案为
(2)(1)中结论成立.理由如下:延长FC到H,使( 连接BH,如图(1).
又 B. , 又∵BF=BF,∴△HBF≌△EBF(SAS),∴HF=EF.∵HF=HC+CF=AE+CF,∴EF=AE+CF.
(3)(1)中的结论不成
立,AE=EF+CF.在AE上
截取AQ=CF,连接BQ,
如图(2). ∵AB⊥AD,
BC⊥CD,∴∠A=∠BCF=90°.∵AB=BC,∴△BCF≌△BAQ(SAS),∴ BF=BQ,
∠CBF=∠ABQ.∵∠MBN=60°=∠CBF+∠CBE,
∴ ∠CBE + ∠ABQ = 60°. ∵∠ABC= 120°,
∴∠QBE=120°-60°=60°=∠MBN,∴∠FBE=
∠QBE. 又∵ BE = BE,∴ △FBE ≌△QBE
(SAS),∴EF=QE,∴AE=QE+AQ=EF+CF.大招解读|费马点模型
“费马点”是指到三角形三个顶点距离之和最小的点.主要分为两种情况:
(1)当三角形三个内角都小于 时,通常将其中一个小三角形绕大三角形的一个顶点旋转(
例如:将 绕A 点逆时针旋转( 得到 ,连接PQ,如图(1),则. 为等边三角形, 即 QE,当B,P,Q,E四点共线时取得最小值,为BE的长,如图(2).
(2)当三角形有一个内角大于或等于 时,费马点就是此内角的顶点
5.【解】(1)∵△ACP'≌△ABP,∴AP'=AP=3,CP'=BP=4,∠AP'C=∠APB.由题意知旋转角∠PAP'= 60°,∴ △APP'为等边三角形, 为直角三角形,且∠PP'C=90°,∴ ∠APB=∠AP'C=∠AP'P+∠PP'C=60°+90°=150°.故答案为150°.
证明如下:如图(1),把△ABE 绕点A 逆时针旋转90°得到△ACE',连接E'F.由旋转的性质得AE'=AE,CE'=BE,∠CAE'= ∠BAE,∠ACE'=∠B,∠EAE'= 90°.
∵∠EAF=45°,∴ ∠E'AF=∠EAE'-∠EAF=
90°-45°=45°,∴∠EAF=∠E'AF.在△EAF
和△E'AF 中, △E'AF(SAS),∴ E'F=EF.∵ ∠CAB=90°,AB=AC,∴∠B=∠ACB=45°,∴ ∠E'CF=45°+45°=90°. 由勾股定理得
(3)如图(2),将△APB 绕点 B 顺时针旋转60°至△A'P'B 处,连接 PP',则 A'B=AB, ∠ABA'= ∠PBP'= 60°. ∵ 在 Rt△ABC 中,∠ACB=90°,AC=1,∠ABC=30°,∴AB=2, 60°,∴ △BPP'是等边三角形,∴BP= PP',∠BPP'=∠BP'P=60°. ∵∠APC=∠CPB=∠BPA=120°,∴ ∠CPB+∠BPP'=∠BP'A'+∠BP'P=120°+60°=180°,∴C,P,A',P'四点共线.∵ ∠ABC=30°,∠ABA'=60°,∴∠CBA'=90°.又∵A'B=AB=2,∴在Rt△A'BC 中,A'C=
母题学大招9手拉手模型
1[2024 浙江杭州期末,中]图(1)是边长分别为a和b(a>b)的两个等边三角形纸片 ABC 和 C'DE 叠放在一起(C与C'重合)组成的图形.
(1)操作:固定△ABC,将△C'DE 绕点 C 按顺时针方向旋转20°,连接AD,BE,如图(2),线段BE 与AD 之间具有怎样的数量关系 证明你的结论.
(2)操作:若将图(1)中的△C'DE,绕点 C 按顺时针方向任意旋转一个角度α,连接AD,BE,如图(3),线段BE与AD 之间是否仍符合(1)中的结论 若是,请证明;若不是,请直接写出BE与AD之间的数量关系.
(3)根据上面的操作过程,请问当α为多少度时 线段AD 的长度最大 最大值是多少 当α为多少度时,线段AD 的长度最小 最小值是多少
子题练变式
2[2024 浙江宁波校级期末,中]【基础巩固】(1)如图(1),在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△AEC≌△ADB.
【尝试应用】(2)如图(2),在△ABC 与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B,D,E三点在一条直线上,AC与BE 交于点 F,若点F为AC中点,
①求∠BEC 的大小;
②若CE=2,求△ACE的面积.
母题学大招10 半角模型
3[2024上海闵行区质检,中]如图,正方形ABCD中,E,F分别在边BC,CD上,且∠EAF=45°,连接 EF,这种模型属于“半角模型”中的一类.在解决“半角模型”问题时,旋转是一种常用的解题方法.例如将△ADF绕点A 顺时针旋转90°得到△ABG,则可以证明“EF=BE+DF”,请写出证明过程.
子题练变式 含60°的半角模型
4[2024 江苏南京质检,中]已知四边形 ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕 B 点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
(1)当∠MBN 绕 B 点旋转到 AE =CF 时(如图(1)),AE,CF,EF 之间的数量关系为
(2)当 E 在AD 上,F 在 DC上,但AE≠CF 时(如图(2)),(1)中结论是否成立 请说明理由.
(3)当 E在AD 延长线上,F在DC延长线上时(如图(3)),(1)中结论是否成立 若不成立,线段AE,CF,EF之间又有怎样的数量关系 请直接写出你的猜想.
母题学大招11 费马点模型
5[2024江苏扬州期末,较难]背景资料:
在已知△ABC 所在平面上求一点 P,使它到三角形的三个顶点的距离之和最小.
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”,
如图(1),当△ABC三个内角均小于120°时,费马点 P 在△ABC 内部,此时∠APB=∠BPC=∠CPA=120°,此时,PA+PB+PC的值最小.
解决问题:
(1)如图(2),等边△ABC 内有一点 P,若点 P到顶点A,B,C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP 绕顶点A旋转到△ACP'处,此时△ACP'≌△ABP,这样就可以利用旋转变换,将三条线段 PA,PB,PC转化到一个三角形中,从而求出∠APB= ;基本运用:
(2)请你利用第(1)题的解答思想方法,解答下面问题:
如图(3),△ABC中,∠CAB=90°,AB=AC,E,F为BC上的点,且∠EAF=45°,判断BE,EF,FC之间的数量关系并证明;
能力提升:
(3)如图(4),在 Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,点 P 为 Rt△ABC 的费马点,连接AP,BP,CP,求PA+PB+PC的值.
手拉手模型是指两个顶角相等的等腰三角形顶角的顶点重合,左底角顶点互连,右底角顶点互连所组成的图形,如图所示.
1.【解】(
证明: 绕点 C 按顺时针方向旋转
与 是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
(2)是.
证明:∵△C'DE 绕点 C 按顺时针方向旋转的角度为α,
∴∠BCE=∠ACD=α.
∵△ABC 与△C'DE是等边三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD.
(3)当点 D 旋转到 CA 的反向延长线上,即α=180°时,线段AD的长度最大,最大值为a+
b.当点 D 在AC边上,即α=0°时,线段AD的长度最小,最小值为a-b.
2.(1)【证明】∵ ∠BAC=∠DAE,∴ ∠BAC-∠BAE=∠DAE-∠BAE,即∠CAE=∠BAD.
在△AEC 和△ADB中,
∴△AEC≌△ADB(SAS).
【解】(2) ①∵ AD = AE, ∠DAE = 90°,∴ ∠ADE=∠AED = 45°,∴ ∠ADB = 180°-∠ADE=180°-45°=135°,同(1)得△AEC≌△ADB(SAS),∴ ∠AEC = ∠ADB = 135°,∴ ∠BEC=∠AEC-∠AED=135°-45°=90°.
②如图,过点 A 作AG⊥DE于点 G, 则 ∠FGA = 90°,由①可知, ∠FEC = 90°,∴ ∠FGA =∠FEC.∵点F为 AC 中点,∴ AF = CF.又 易得
大招解读|半角模型
半角模型特征:①共端点的等线段;②共顶点的倍半角.通过旋转或作辅助线可以构造全等三角形.常见的半角模型有 角含 角和 角含 角.半角模型在实际应用中会证两次全等,如图, 和
3.【解】∵ 四边形ABCD为正方形,∴AB=AD,∠ADF=∠ABE=90°.∵△ADF 绕点 A 顺时针旋转 90°得到 △ABG,∴ △ADF≌ △ABG,∴AF=AG,BG=DF,∠DAF=∠GAB,∠ABG=∠ADF=90°,∴∠ABG+∠ABC=180°,∴G,B,E共线. ∵∠EAF=45°, ∴∠DAF+∠EAB =45°,∴∠GAB+∠EAB=45°,∴∠GAE=∠EAF=
45°. 在 △AGE 和 △AFE 中,
∴△AGE≌△AFE(SAS),∴GE=EF,∴EF=GE=BE+GB=BE+DF.
4.【解】(1)∵AB⊥AD,BC⊥CD,∴∠A=∠C=90°.∵AB=BC,AE=CF,∴ △ABE≌△CBF(SAS),∴ ∠ABE=∠CBF,BE=BF.∵ ∠ABC= BF,∴△BEF是等边三角形, 故答案为
(2)(1)中结论成立.理由如下:延长FC到H,使( 连接BH,如图(1).
又 B. , 又∵BF=BF,∴△HBF≌△EBF(SAS),∴HF=EF.∵HF=HC+CF=AE+CF,∴EF=AE+CF.
(3)(1)中的结论不成
立,AE=EF+CF.在AE上
截取AQ=CF,连接BQ,
如图(2). ∵AB⊥AD,
BC⊥CD,∴∠A=∠BCF=90°.∵AB=BC,∴△BCF≌△BAQ(SAS),∴ BF=BQ,
∠CBF=∠ABQ.∵∠MBN=60°=∠CBF+∠CBE,
∴ ∠CBE + ∠ABQ = 60°. ∵∠ABC= 120°,
∴∠QBE=120°-60°=60°=∠MBN,∴∠FBE=
∠QBE. 又∵ BE = BE,∴ △FBE ≌△QBE
(SAS),∴EF=QE,∴AE=QE+AQ=EF+CF.大招解读|费马点模型
“费马点”是指到三角形三个顶点距离之和最小的点.主要分为两种情况:
(1)当三角形三个内角都小于 时,通常将其中一个小三角形绕大三角形的一个顶点旋转(
例如:将 绕A 点逆时针旋转( 得到 ,连接PQ,如图(1),则. 为等边三角形, 即 QE,当B,P,Q,E四点共线时取得最小值,为BE的长,如图(2).
(2)当三角形有一个内角大于或等于 时,费马点就是此内角的顶点
5.【解】(1)∵△ACP'≌△ABP,∴AP'=AP=3,CP'=BP=4,∠AP'C=∠APB.由题意知旋转角∠PAP'= 60°,∴ △APP'为等边三角形, 为直角三角形,且∠PP'C=90°,∴ ∠APB=∠AP'C=∠AP'P+∠PP'C=60°+90°=150°.故答案为150°.
证明如下:如图(1),把△ABE 绕点A 逆时针旋转90°得到△ACE',连接E'F.由旋转的性质得AE'=AE,CE'=BE,∠CAE'= ∠BAE,∠ACE'=∠B,∠EAE'= 90°.
∵∠EAF=45°,∴ ∠E'AF=∠EAE'-∠EAF=
90°-45°=45°,∴∠EAF=∠E'AF.在△EAF
和△E'AF 中, △E'AF(SAS),∴ E'F=EF.∵ ∠CAB=90°,AB=AC,∴∠B=∠ACB=45°,∴ ∠E'CF=45°+45°=90°. 由勾股定理得
(3)如图(2),将△APB 绕点 B 顺时针旋转60°至△A'P'B 处,连接 PP',则 A'B=AB, ∠ABA'= ∠PBP'= 60°. ∵ 在 Rt△ABC 中,∠ACB=90°,AC=1,∠ABC=30°,∴AB=2, 60°,∴ △BPP'是等边三角形,∴BP= PP',∠BPP'=∠BP'P=60°. ∵∠APC=∠CPB=∠BPA=120°,∴ ∠CPB+∠BPP'=∠BP'A'+∠BP'P=120°+60°=180°,∴C,P,A',P'四点共线.∵ ∠ABC=30°,∠ABA'=60°,∴∠CBA'=90°.又∵A'B=AB=2,∴在Rt△A'BC 中,A'C=
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
