第三章 图形的平移与旋转 中考考点训练(含解析) 2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 第三章 图形的平移与旋转 中考考点训练(含解析) 2024-2025学年北师大版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 16:45:18 | ||
图片预览



文档简介
图形的平移与旋转中考考点训练
考点1 图形变换的定义及性质
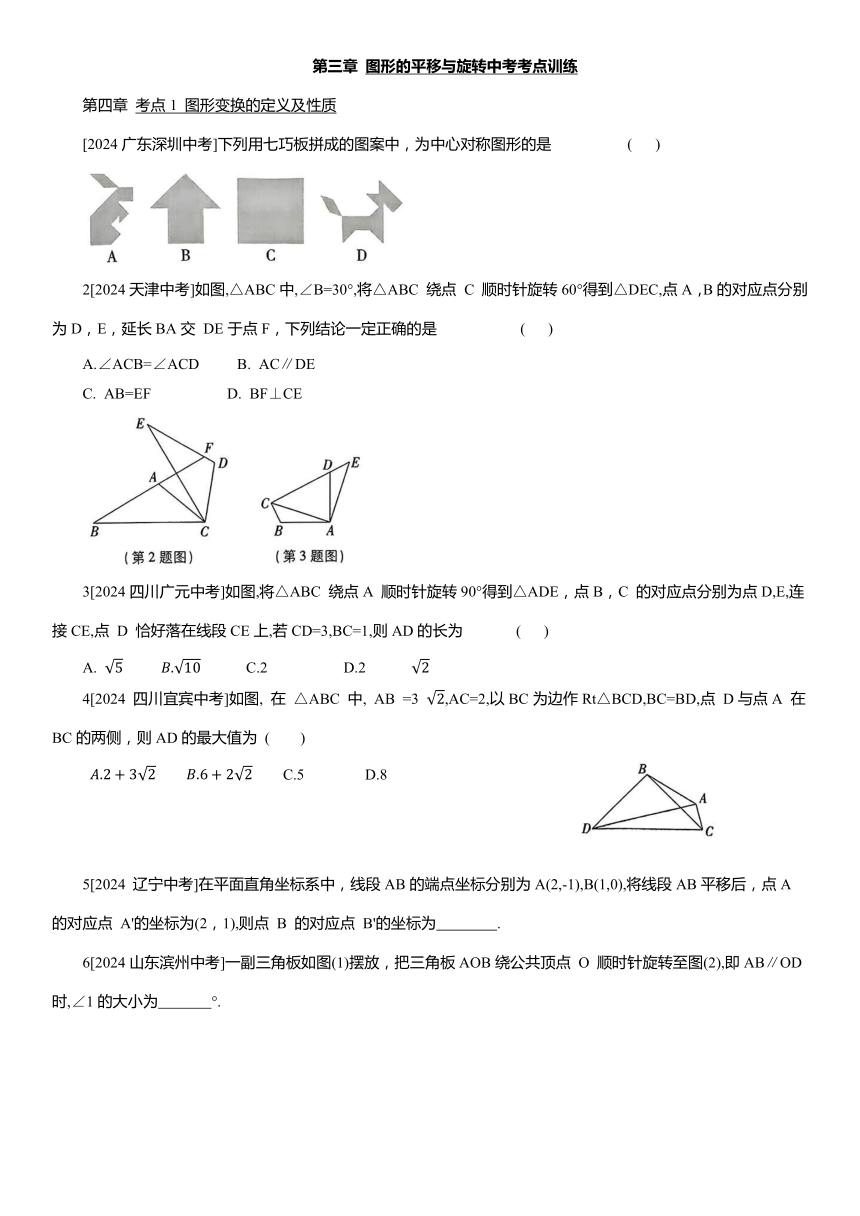
[2024广东深圳中考]下列用七巧板拼成的图案中,为中心对称图形的是 ( )
2[2024天津中考]如图,△ABC中,∠B=30°,将△ABC 绕点 C 顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交 DE于点F,下列结论一定正确的是 ( )
A.∠ACB=∠ACD B. AC∥DE
C. AB=EF D. BF⊥CE
3[2024四川广元中考]如图,将△ABC 绕点A 顺时针旋转90°得到△ADE,点B,C 的对应点分别为点D,E,连接CE,点 D 恰好落在线段CE上,若CD=3,BC=1,则AD的长为 ( )
A. C.2 D.2
4[2024 四川宜宾中考]如图, 在 △ABC 中, AB =3 ,AC=2,以BC为边作Rt△BCD,BC=BD,点 D与点A 在BC的两侧,则AD的最大值为 ( )
C.5 D.8
5[2024 辽宁中考]在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB平移后,点A 的对应点 A'的坐标为(2,1),则点 B 的对应点 B'的坐标为 .
6[2024山东滨州中考]一副三角板如图(1)摆放,把三角板AOB绕公共顶点 O 顺时针旋转至图(2),即AB∥OD时,∠1的大小为 °.
7[2024北京中考]已知 点B,C分别在射线AN,AM 上,将线段BC绕点B顺时针旋转180°-2α得到线段BD,过点D作AN的垂线交射线AM 于点 E.
(1)如图(1),当点 D 在射线AN上时,求证:C是AE的中点;
(2)如图(2),当点 D 在∠MAN内部时,作DF∥AN,交射线AM于点 F,用等式表示线段 EF 与AC 的数量关系,并证明.
8[2024 黑龙江牡丹江中考]数学老师在课堂上给出了一个问题,让同学们探究.在 Rt△ABC中,∠ACB=90°,∠BAC=30°,点 D 在直线 BC上,将线段AD 绕点A 顺时针旋转60°得到线段AE,过点 E作EF∥BC,交直线AB 于点 F.
(1)当点 D 在线段 BC 上时,如图(1),求证:BD+EF=AB.
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB 上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论.
推理证明:写出图(1)的证明过程.
探究问题:
(2)当点D 在线段BC 的延长线上时,如图(2);当点 D 在线段 CB 的延长线上时,如图(3),请判断并直接写出线段 BD,EF,AB 之间的数量关系.
拓展思考:
(3)在(1)(2)的条件下,若 2BD,则EF= .
考点2 图形变换的作图
[2023安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点).
(1)画出线段 AB 关于直线 CD 对称的线段A B ;
(2)将线段AB 向左平移2个单位长度,再向上平移1个单位长度,得到线段A B ,画出线段A B ;
(3)描出线段AB上的点 M 及直线 CD 上的点N,使得直线MN垂直平分AB.
10[2024安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D 为旋转中心,将△ABC 旋转180°得到△A B C ,画出△A B C ;
(2)直接写出以B,C ,B ,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点 E,使得射线AE平分∠BAC,写出点 E 的坐标.
1. C【解析】选项 A、B、D均不能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以不是中心对称图形;选项C能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以是中心对称图形.故选 C.
2. D 【解析】记 BF 与CE相交于点H,如图所示.∵将 绕点C顺时针旋转( 得到
∵ ∠B=30°,∴ 在△BHC
中,∠BHC=180°-∠BCE-∠B=90°,∴BF⊥CE,故D 选项正确,符合题意.设∠ACH=x°,
∴∠ACB=60°-x°.∵ ∠B=30°,∴ ∠EDC=∠BAC= 180°-30°-(60°-x°) = 90°+x°,
∵x°不一定等于30°,∴ ∠EDC+∠ACD 不一定等于180°,∴AC∥DE 不一定成立,故B选项不正确,不符合题意.∵ ∠ACB=60°-x°,∠ACD=60°,x°不一定等于 0°,∴∠ACB =∠ACD 不一定成立,故A 选项不正确,不符合题意.∵将△ABC 绕点 C 顺时针旋转60°得到△DEC,∴AB=ED=EF+FD,∴ BA≥EF,故C选项不正确,不符合题意.故选 D.
3. A 【解析】由旋转得 △ABC ≌ △ADE,∠CAE=90°,AC=AE,DE=BC=1,∴ △ACE是等腰直角三角形,CE=CD+DE=3+1=4.如图,过点A作AH⊥CE 于点 H, CH=HE=2,∴HD=HE-DE=2-1=1,∴AD= 故选A.
4. D 【解析】将 BA 绕点 B 顺时针旋转90°,得
到BE,连接AE,DE,∴ BE=AB,∠ABE=90°,
∴ 由勾股定理得 AE =6. ∵∠DBC =90°=∠EBA,∴∠DBE+∠EBC = ∠CBA+∠EBC,
∴ ∠DBE=∠CBA. 又∵ BD =BC,BE=AB,
∴ △DBE≌△CBA (SAS),∴DE = AC = 2.
∵AD≤AE+DE,∴当A,D,E 三点共线时,AD有最大值,∴ AD的最大值为AE+DE=6+2=8.故选 D.
5.(1,2) 【解析】因为点A的坐标为(2,-1),平移后对应点A'的坐标为(2,1),所以线段AB 向上平移2个单位长度,所以点B(1,0)的对应点 B'的坐标为(1,2).故答案为(1,2).
6.75 【解析】由已知可得,∠D=30°,∠B=45°.∵AB∥OD,∴∠B=∠BOD=45°,∴∠1=∠BOD+∠D=45°+30°=75°.故答案为75.
7.(1)【证明】连接 CD.由题意得 BC = BD,∠CBD = 180° - 2α, ∴ ∠BDC = ∠BCD.
∵∠BDC+∠BCD+∠CBD=180°,∴∠BDC=
∴CA=CD.∵ED⊥AN,∴ ∠CED+∠MAN=
∠CDE +∠BDC = 90°,∴∠CED = ∠CDE,∴CD=CE,∴CA=CE,∴点C是AE的中点.
(2)【解】EF=2AC.证明:如图,在射线AM上取点H,使得 BH=BA,取 EF 的中点 G,连接DG,DH. ∵ BH = BA,∴∠BAH=∠BHA=α,∴∠ABH = 180°-2α= ∠CBD,∴∠ABC =∠HBD. 又∵ BC= BD,∴ △ABC≌△HBD,∴AC= DH, ∠BHD = ∠A = α,∴∠FHD =∠BHA+∠BHD=2α.∵ DF∥AN,∴ ∠EFD=∠A=α,∠EDF=∠1=90°.∵ G 是 EF 的中点,∴GF=GD,EF=2GD,∴∠GFD=∠GDF=α,∴∠HGD=2α,∴ ∠HGD=∠FHD,∴DG=DH.∵AC=DH,∴DG=AC,∴EF=2AC.
8.(1)【证明】由题意得,∠B=90°-∠BAC=90°-30°=60°.∵EF∥BC,∴ ∠EFB=∠B=60°.又∵ ∠EAD=60°,∴∠EFB=∠EAD. 又∵∠BAD=∠EAD-∠EAF,∠AEF=∠EFB-∠EAF,∴∠BAD=∠AEF.又∵AD=AE,AM=EF,∴ △DAM≌△AEF(SAS),∴ AF=DM,∠AMD=∠EFA=180°-∠EFB=180°-60°=120°,∴∠BMD=180°-∠AMD=180°-120°=60°.∵∠B=60°,∴ ∠BMD=∠B=∠BDM=60°,∴ △BMD 是等边三角形,∴ BD=BM=DM.∵AB=AM+BM,∴AB=EF+BD.
【解】(2)当点 D 在线段 BC 的延长线上时,AB=BD-EF;当点 D 在线段CB 的延长线上时,AB=EF-BD.如图(1),点D 在线段BC的延长线上时,在 BD 上取点 H,使BH=AB,连接AH 并延长到点 G 使AG=AF,连接 DG.
∵∠ABC=60°,∴ △ABH 是等边三角形,
∴∠BAH=60°.∵线段AD绕点A 顺时针旋转60°得到线段 AE,∴ ∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,∴∠BAH-∠EAH=∠DAE-∠EAH,即 ∠BAE = ∠HAD. 又∵ AG = AF,
∴△FAE≌△GAD(SAS),∴EF=DG,∠AFE=∠G.∵BD∥EF,∴ ∠ABC=∠F=∠G=60°.
∵∠DHG=∠AHB=60°,∴ △DHG 是等边三角形,∴DH=DG=EF,∴AB=BH=BD-DH=
BD-EF.如图(2),点 D 在线段 CB 的延长线上时,在EF上取点P 使AP=AF.∵EF∥BC,
∴∠F=∠ABC=60°.∵AP=AF,∴ △APF 是等边 三角形, ∴ ∠APF = ∠PAF = 60°,
∴ ∠APE=120°.∵ 将线段AD 绕点 A 顺时针旋转60°得到线段 AE,∴ AD=AE,∠DAE=60°,∴ ∠DAB + ∠EAP = 180° - ∠EAD -
∠PAF=60°.∵ ∠D+∠DAB =∠ABC=60°,
∴ ∠D =∠EAP.∵ ∠DBA = 180°-∠ABC =120°= ∠EPA,AD =AE,∴ △EAP≌△ADB
(AAS),∴ BD =AP,AB = EP.∵ AP = FP,
如题图(1),
由
(1)可知, .如图(1),当点 D 在线段 BC 的延长线上时, 与 矛盾,∴不符合题意.如图(2),当点 D 在线段 CB 的延长线上时, = 综上所述, 或18,故答案为10或18.
9.【解】(1)如图所示,线段 即为所求.
(2)如图所示,线段. 即为所求.
(3)如图所示,点M,N即为所求.
【解】(1)如图, 即为所求.
(2)如图,以B, C为顶点的四边形的面积为
(3)点E 如图所示,点E 的坐标可以为(3,0)(或(4,2)或(5,4)或(6,6)).(答案不唯一,写出一个即可)
考点1 图形变换的定义及性质
[2024广东深圳中考]下列用七巧板拼成的图案中,为中心对称图形的是 ( )
2[2024天津中考]如图,△ABC中,∠B=30°,将△ABC 绕点 C 顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交 DE于点F,下列结论一定正确的是 ( )
A.∠ACB=∠ACD B. AC∥DE
C. AB=EF D. BF⊥CE
3[2024四川广元中考]如图,将△ABC 绕点A 顺时针旋转90°得到△ADE,点B,C 的对应点分别为点D,E,连接CE,点 D 恰好落在线段CE上,若CD=3,BC=1,则AD的长为 ( )
A. C.2 D.2
4[2024 四川宜宾中考]如图, 在 △ABC 中, AB =3 ,AC=2,以BC为边作Rt△BCD,BC=BD,点 D与点A 在BC的两侧,则AD的最大值为 ( )
C.5 D.8
5[2024 辽宁中考]在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB平移后,点A 的对应点 A'的坐标为(2,1),则点 B 的对应点 B'的坐标为 .
6[2024山东滨州中考]一副三角板如图(1)摆放,把三角板AOB绕公共顶点 O 顺时针旋转至图(2),即AB∥OD时,∠1的大小为 °.
7[2024北京中考]已知 点B,C分别在射线AN,AM 上,将线段BC绕点B顺时针旋转180°-2α得到线段BD,过点D作AN的垂线交射线AM 于点 E.
(1)如图(1),当点 D 在射线AN上时,求证:C是AE的中点;
(2)如图(2),当点 D 在∠MAN内部时,作DF∥AN,交射线AM于点 F,用等式表示线段 EF 与AC 的数量关系,并证明.
8[2024 黑龙江牡丹江中考]数学老师在课堂上给出了一个问题,让同学们探究.在 Rt△ABC中,∠ACB=90°,∠BAC=30°,点 D 在直线 BC上,将线段AD 绕点A 顺时针旋转60°得到线段AE,过点 E作EF∥BC,交直线AB 于点 F.
(1)当点 D 在线段 BC 上时,如图(1),求证:BD+EF=AB.
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB 上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论.
推理证明:写出图(1)的证明过程.
探究问题:
(2)当点D 在线段BC 的延长线上时,如图(2);当点 D 在线段 CB 的延长线上时,如图(3),请判断并直接写出线段 BD,EF,AB 之间的数量关系.
拓展思考:
(3)在(1)(2)的条件下,若 2BD,则EF= .
考点2 图形变换的作图
[2023安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点).
(1)画出线段 AB 关于直线 CD 对称的线段A B ;
(2)将线段AB 向左平移2个单位长度,再向上平移1个单位长度,得到线段A B ,画出线段A B ;
(3)描出线段AB上的点 M 及直线 CD 上的点N,使得直线MN垂直平分AB.
10[2024安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D 为旋转中心,将△ABC 旋转180°得到△A B C ,画出△A B C ;
(2)直接写出以B,C ,B ,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点 E,使得射线AE平分∠BAC,写出点 E 的坐标.
1. C【解析】选项 A、B、D均不能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以不是中心对称图形;选项C能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以是中心对称图形.故选 C.
2. D 【解析】记 BF 与CE相交于点H,如图所示.∵将 绕点C顺时针旋转( 得到
∵ ∠B=30°,∴ 在△BHC
中,∠BHC=180°-∠BCE-∠B=90°,∴BF⊥CE,故D 选项正确,符合题意.设∠ACH=x°,
∴∠ACB=60°-x°.∵ ∠B=30°,∴ ∠EDC=∠BAC= 180°-30°-(60°-x°) = 90°+x°,
∵x°不一定等于30°,∴ ∠EDC+∠ACD 不一定等于180°,∴AC∥DE 不一定成立,故B选项不正确,不符合题意.∵ ∠ACB=60°-x°,∠ACD=60°,x°不一定等于 0°,∴∠ACB =∠ACD 不一定成立,故A 选项不正确,不符合题意.∵将△ABC 绕点 C 顺时针旋转60°得到△DEC,∴AB=ED=EF+FD,∴ BA≥EF,故C选项不正确,不符合题意.故选 D.
3. A 【解析】由旋转得 △ABC ≌ △ADE,∠CAE=90°,AC=AE,DE=BC=1,∴ △ACE是等腰直角三角形,CE=CD+DE=3+1=4.如图,过点A作AH⊥CE 于点 H, CH=HE=2,∴HD=HE-DE=2-1=1,∴AD= 故选A.
4. D 【解析】将 BA 绕点 B 顺时针旋转90°,得
到BE,连接AE,DE,∴ BE=AB,∠ABE=90°,
∴ 由勾股定理得 AE =6. ∵∠DBC =90°=∠EBA,∴∠DBE+∠EBC = ∠CBA+∠EBC,
∴ ∠DBE=∠CBA. 又∵ BD =BC,BE=AB,
∴ △DBE≌△CBA (SAS),∴DE = AC = 2.
∵AD≤AE+DE,∴当A,D,E 三点共线时,AD有最大值,∴ AD的最大值为AE+DE=6+2=8.故选 D.
5.(1,2) 【解析】因为点A的坐标为(2,-1),平移后对应点A'的坐标为(2,1),所以线段AB 向上平移2个单位长度,所以点B(1,0)的对应点 B'的坐标为(1,2).故答案为(1,2).
6.75 【解析】由已知可得,∠D=30°,∠B=45°.∵AB∥OD,∴∠B=∠BOD=45°,∴∠1=∠BOD+∠D=45°+30°=75°.故答案为75.
7.(1)【证明】连接 CD.由题意得 BC = BD,∠CBD = 180° - 2α, ∴ ∠BDC = ∠BCD.
∵∠BDC+∠BCD+∠CBD=180°,∴∠BDC=
∴CA=CD.∵ED⊥AN,∴ ∠CED+∠MAN=
∠CDE +∠BDC = 90°,∴∠CED = ∠CDE,∴CD=CE,∴CA=CE,∴点C是AE的中点.
(2)【解】EF=2AC.证明:如图,在射线AM上取点H,使得 BH=BA,取 EF 的中点 G,连接DG,DH. ∵ BH = BA,∴∠BAH=∠BHA=α,∴∠ABH = 180°-2α= ∠CBD,∴∠ABC =∠HBD. 又∵ BC= BD,∴ △ABC≌△HBD,∴AC= DH, ∠BHD = ∠A = α,∴∠FHD =∠BHA+∠BHD=2α.∵ DF∥AN,∴ ∠EFD=∠A=α,∠EDF=∠1=90°.∵ G 是 EF 的中点,∴GF=GD,EF=2GD,∴∠GFD=∠GDF=α,∴∠HGD=2α,∴ ∠HGD=∠FHD,∴DG=DH.∵AC=DH,∴DG=AC,∴EF=2AC.
8.(1)【证明】由题意得,∠B=90°-∠BAC=90°-30°=60°.∵EF∥BC,∴ ∠EFB=∠B=60°.又∵ ∠EAD=60°,∴∠EFB=∠EAD. 又∵∠BAD=∠EAD-∠EAF,∠AEF=∠EFB-∠EAF,∴∠BAD=∠AEF.又∵AD=AE,AM=EF,∴ △DAM≌△AEF(SAS),∴ AF=DM,∠AMD=∠EFA=180°-∠EFB=180°-60°=120°,∴∠BMD=180°-∠AMD=180°-120°=60°.∵∠B=60°,∴ ∠BMD=∠B=∠BDM=60°,∴ △BMD 是等边三角形,∴ BD=BM=DM.∵AB=AM+BM,∴AB=EF+BD.
【解】(2)当点 D 在线段 BC 的延长线上时,AB=BD-EF;当点 D 在线段CB 的延长线上时,AB=EF-BD.如图(1),点D 在线段BC的延长线上时,在 BD 上取点 H,使BH=AB,连接AH 并延长到点 G 使AG=AF,连接 DG.
∵∠ABC=60°,∴ △ABH 是等边三角形,
∴∠BAH=60°.∵线段AD绕点A 顺时针旋转60°得到线段 AE,∴ ∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,∴∠BAH-∠EAH=∠DAE-∠EAH,即 ∠BAE = ∠HAD. 又∵ AG = AF,
∴△FAE≌△GAD(SAS),∴EF=DG,∠AFE=∠G.∵BD∥EF,∴ ∠ABC=∠F=∠G=60°.
∵∠DHG=∠AHB=60°,∴ △DHG 是等边三角形,∴DH=DG=EF,∴AB=BH=BD-DH=
BD-EF.如图(2),点 D 在线段 CB 的延长线上时,在EF上取点P 使AP=AF.∵EF∥BC,
∴∠F=∠ABC=60°.∵AP=AF,∴ △APF 是等边 三角形, ∴ ∠APF = ∠PAF = 60°,
∴ ∠APE=120°.∵ 将线段AD 绕点 A 顺时针旋转60°得到线段 AE,∴ AD=AE,∠DAE=60°,∴ ∠DAB + ∠EAP = 180° - ∠EAD -
∠PAF=60°.∵ ∠D+∠DAB =∠ABC=60°,
∴ ∠D =∠EAP.∵ ∠DBA = 180°-∠ABC =120°= ∠EPA,AD =AE,∴ △EAP≌△ADB
(AAS),∴ BD =AP,AB = EP.∵ AP = FP,
如题图(1),
由
(1)可知, .如图(1),当点 D 在线段 BC 的延长线上时, 与 矛盾,∴不符合题意.如图(2),当点 D 在线段 CB 的延长线上时, = 综上所述, 或18,故答案为10或18.
9.【解】(1)如图所示,线段 即为所求.
(2)如图所示,线段. 即为所求.
(3)如图所示,点M,N即为所求.
【解】(1)如图, 即为所求.
(2)如图,以B, C为顶点的四边形的面积为
(3)点E 如图所示,点E 的坐标可以为(3,0)(或(4,2)或(5,4)或(6,6)).(答案不唯一,写出一个即可)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
