数学:1.2.2《解斜三角形应用举例》课件(新人教a版必修5)
文档属性
| 名称 | 数学:1.2.2《解斜三角形应用举例》课件(新人教a版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 541.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-11 00:00:00 | ||
图片预览






文档简介
课件17张PPT。新课标人教版课件系列《高中数学》
必修51.2.2《解斜三角形应用举例》审校:王伟教学目标 1、能够运用正弦定理、余弦定理等知识和方法解决一些有关底部不可到达的物体高度测量的问题
2、巩固深化解三角形实际问题的一般方法,养成良好的研究、探索习惯。
3、进一步培养学生学习数学、应用数学的意识及观察、归纳、类比、概括的能力
二、教学重点、难点
重点:结合实际测量工具,解决生活中的测量高度问题
难点:能观察较复杂的图形,从中找到解决问题的关键条件基础知识复习解斜三角形应用举例1、正弦定理2、余弦定理解斜三角形应用举例解应用题的一般步骤1.审题
理解题意,明确背景,熟悉已知条件,了解所需要的条件(或量),明确试题的所求内容.
2.建立数学模型
把实际问题转化为数学问题.
3.解答数学模型
解答数学问题.
4.总结
与问题所求量进行联系,总结作答. 斜三角形应用题的解题要点
解斜三角形的问题,通常都要根据题意,从实际问题中寻找
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
从而得到实际问题的解。解斜三角形应用举例高一九班
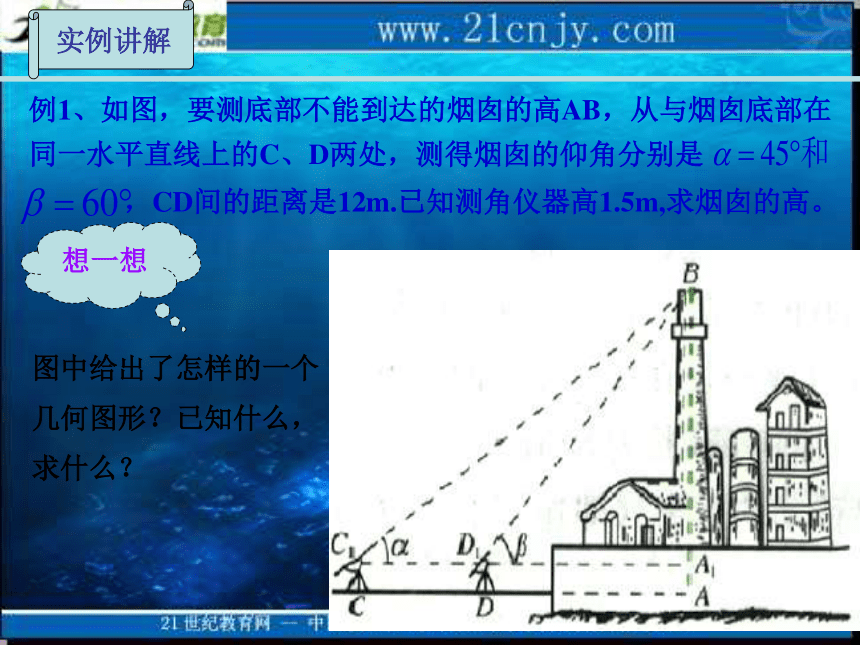
2004.5实例讲解例1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m.例2、自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。实例讲解想一想 本题解法二提示
亦可先设出A1B与A1D1的长分别为x和y,利用直角△BD1A1
与直角△BC1A1的边角的正切关系求解。实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.分析实例2、如图,一艘船以32.2 nmile/h的速度
向正北航行, 在A处看灯塔S在船的
北偏东 ,30min后航行到B处,在B
处看灯塔S在船的北偏东 方向上,
求灯塔S和B处的距离(精确到0.1nmile).第1题第2题3291m7.8 n mile实例讲解 例3. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).自我分析3、下图为曲柄连杠机构示意图,当曲柄OA在水平位置OB时,
连杠端点P在Q的位置 .当OA自OB按顺时针方向旋转角时,P和Q之间的距离是.已知OA=25cm,AP=125cm,分别求下列条件下的 值(精确到0.1cm)(1)(2)(3)(4)课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解布置作业《导与练》P134-135
A级的第1,10题 B级的第1,8题
(要求:以大题的形式解答)再见
必修51.2.2《解斜三角形应用举例》审校:王伟教学目标 1、能够运用正弦定理、余弦定理等知识和方法解决一些有关底部不可到达的物体高度测量的问题
2、巩固深化解三角形实际问题的一般方法,养成良好的研究、探索习惯。
3、进一步培养学生学习数学、应用数学的意识及观察、归纳、类比、概括的能力
二、教学重点、难点
重点:结合实际测量工具,解决生活中的测量高度问题
难点:能观察较复杂的图形,从中找到解决问题的关键条件基础知识复习解斜三角形应用举例1、正弦定理2、余弦定理解斜三角形应用举例解应用题的一般步骤1.审题
理解题意,明确背景,熟悉已知条件,了解所需要的条件(或量),明确试题的所求内容.
2.建立数学模型
把实际问题转化为数学问题.
3.解答数学模型
解答数学问题.
4.总结
与问题所求量进行联系,总结作答. 斜三角形应用题的解题要点
解斜三角形的问题,通常都要根据题意,从实际问题中寻找
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
从而得到实际问题的解。解斜三角形应用举例高一九班
2004.5实例讲解例1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m.例2、自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。实例讲解想一想 本题解法二提示
亦可先设出A1B与A1D1的长分别为x和y,利用直角△BD1A1
与直角△BC1A1的边角的正切关系求解。实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.分析实例2、如图,一艘船以32.2 nmile/h的速度
向正北航行, 在A处看灯塔S在船的
北偏东 ,30min后航行到B处,在B
处看灯塔S在船的北偏东 方向上,
求灯塔S和B处的距离(精确到0.1nmile).第1题第2题3291m7.8 n mile实例讲解 例3. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).自我分析3、下图为曲柄连杠机构示意图,当曲柄OA在水平位置OB时,
连杠端点P在Q的位置 .当OA自OB按顺时针方向旋转角时,P和Q之间的距离是.已知OA=25cm,AP=125cm,分别求下列条件下的 值(精确到0.1cm)(1)(2)(3)(4)课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解布置作业《导与练》P134-135
A级的第1,10题 B级的第1,8题
(要求:以大题的形式解答)再见
