【小升初真题汇编】重庆市适用:应用题(专项训练)(含解析)-2024-2025学年六年级下册数学 西师大版
文档属性
| 名称 | 【小升初真题汇编】重庆市适用:应用题(专项训练)(含解析)-2024-2025学年六年级下册数学 西师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 21:23:21 | ||
图片预览




文档简介
重庆市小升初真题汇编:应用题
2024-2025学年六年级下册数学西师大版
1.(2024 渝中区)有A、B、C三种盐水,按A与B数量之比2:1混合,得到浓度为13%的盐水;按A与B的数量之比为1:2混合,得到浓度为14%的盐水。如果A、B、C数量之比为1:1:3,混合成的盐水浓度为10.2%。问:盐水C的浓度是多少?
2.(2024 渝中区)一段地下管道预计15个工人每天工作4小时,18天可以完成,后来要求加快速度每天增加3人,并且每天工作时间增加1小时,那么,可以提前几天完成?
3.(2024 丰都县)如图是2024年我县某校三至六年级学生人数统计情况。认真读题,完成后面的问题。
(1)图中,单位“1”是 。
A.三至六年级学生总人数
B.五年级学生人数
(2)算一算,该校五年级学生人数占三至六年级学生总人数的 %。
(3)根据上面的统计图,完善下面的统计表。
年级 三年级 四年级 五年级 六年级
人数 84 100
(4)仔细思考,该校学生人数从六年级到三年级,呈现出的发展趋势是 。
A.逐年增长
B.逐年减少
4.(2024 沙坪坝区)某商场今天卖出男、女皮衣各一件,现价都是990元,其中女式皮衣款式漂亮赚了10%,男式皮衣款式陈旧赔了10%,今天卖出这两件皮衣是赚钱还是赔钱?若是赚钱,赚了多少?若是赔钱,赔了多少?
5.(2024 涪陵区)有一种陀螺(如图),上半部分是圆柱,下半部分是圆锥。经过测试,当圆柱的体积与圆锥的体积之比为4:1时,陀螺会转得又稳又快。已知圆锥的底面直径是4厘米,高是1.5厘米。请你算一算,这个陀螺的体积是多少时才能使陀螺转得又稳又快?(π取3.14)
6.(2023 沙坪坝区)李师傅加工一批零件,第一天加工了48个,第二天比第一天多加工25%,第三天比第二天多加工5%,三天共完成这批零件的95%.这批零件共有多少个?
7.(2017 白银)如图所示,AB=12厘米,ED=DA=6厘米,小虫P从A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.
(1)小虫P从A点出发几秒后,三角形APE是等腰直角三角形?
(2)当小虫P到达C时,另一只小虫Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①小虫Q从A点出发几秒后,四边形AQPE是梯形?
②当∠QPD=45度时,四边形AQPE的面积是多少平方厘米?
8.(2024 渝北区)一个水果商从外地运回2000千克苹果,进价是每千克4元,运费及其他支出是1000元.售完这批水果要损耗25%.
(1)如果要不亏本,每千克苹果至少应卖多少元?
(2)如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利多少元?
9.(2024 沙坪坝区)有一些相同的房间需要粉刷一天,4名师傅去粉刷8个房间,结果其中有40平方米的墙面未来得及刷;同样的时间6名徒弟刷9个房间的墙面。每名师傅比徒弟一天多刷20平方米的墙面。
(1)求每个房间需要粉刷的墙面面积。
(2)某老板现有40个这样的房间需要粉刷,若请3名师傅带3名徒弟去,需要几天完成?
(3)已知每名师傅、每名徒弟每天的工资分别是85元、65元,老板要求在3天内完成40个房间的粉刷任务。问:如何在10个人以内雇佣人员最合算?最低费用是多少?(10人不一定全部雇佣)
10.(2024 渝北区)六年级小语种选修班开课了。第一周参加日语班的男生比女生多10人,第二周参加日语班的男生比第一周少,参加日语班的女生比第一周多,第二周参加日语班课的男生和女生一共有59人,问第一周参加日语班学习的男生和女生各有多少人?
11.(2022 凤凰县)市政府要求地铁集团过江隧道工程12个月完工.现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元.由于前期工程路面较宽,可由甲、乙两队共同施工.随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对中山大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
(1)求两套方案中m和n的值;
(2)通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
12.(2024 九龙坡区)(附加题).右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状,请你计算出它的体积.
13.(2024 九龙坡区)实验小学举行庆“六一”男女大合唱,原计划合唱队中女生人数占合唱队总人数的,后来考虑到合唱效果,将增加5名男生,这时女生与男生人数的比是6:5.合唱队原有女生多少名?
14.(2024 石柱县)如图是小伟跳远时留下的脚印。如果你是裁判员,该怎样测量他的成绩?请在图中画出待测量的线段。
15.(2024 渝北区)如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm.由此可得到木棒长为 cm。
(2)由题(1)的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年才出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁?
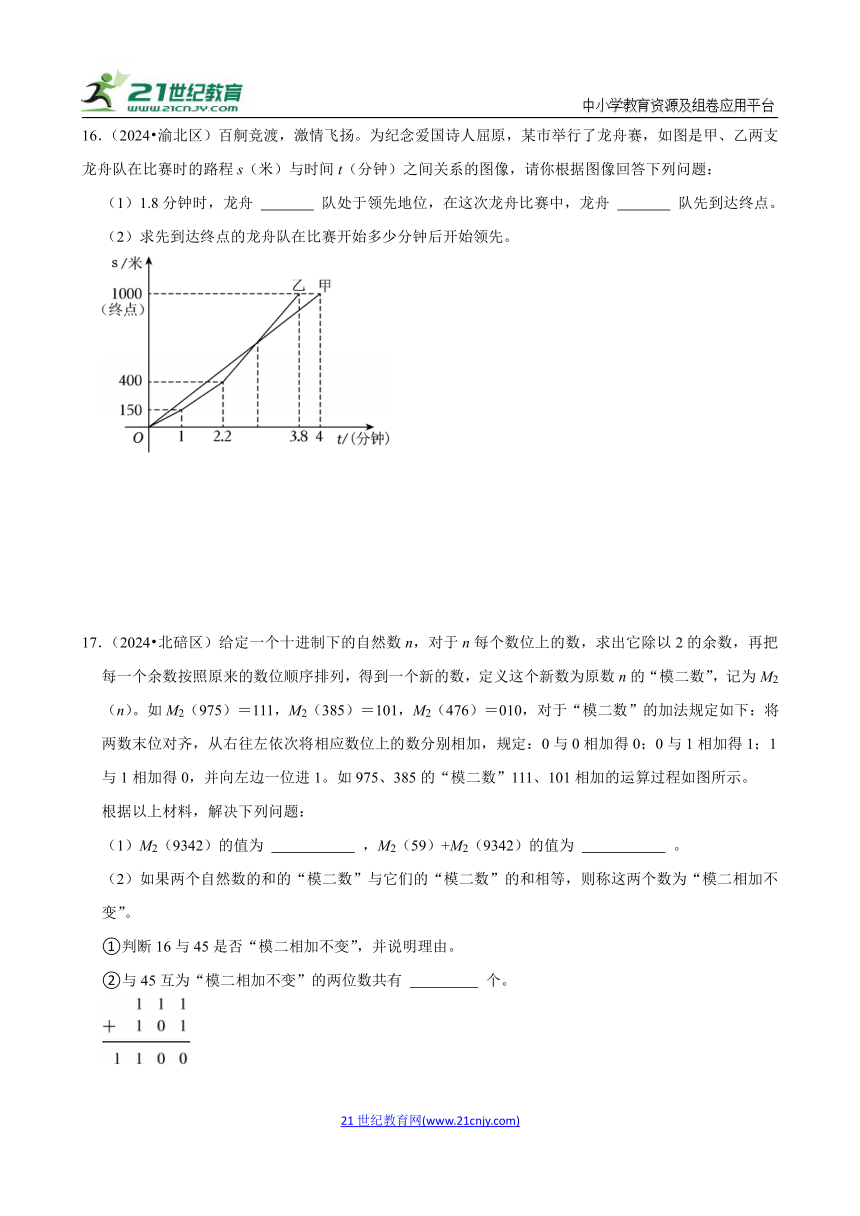
16.(2024 渝北区)百舸竞渡,激情飞扬。为纪念爱国诗人屈原,某市举行了龙舟赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间关系的图像,请你根据图像回答下列问题:
(1)1.8分钟时,龙舟 队处于领先地位,在这次龙舟比赛中,龙舟 队先到达终点。
(2)求先到达终点的龙舟队在比赛开始多少分钟后开始领先。
17.(2024 北碚区)给定一个十进制下的自然数n,对于n每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数n的“模二数”,记为M2(n)。如M2(975)=111,M2(385)=101,M2(476)=010,对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1。如975、385的“模二数”111、101相加的运算过程如图所示。
根据以上材料,解决下列问题:
(1)M2(9342)的值为 ,M2(59)+M2(9342)的值为 。
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数为“模二相加不变”。
①判断16与45是否“模二相加不变”,并说明理由。
②与45互为“模二相加不变”的两位数共有 个。
18.(2024 垫江县)推导圆柱的体积。
将圆柱如图切分后拼成一个近似的长方体。切拼前后,圆柱的体积没有发生改变,表面积增加了。
(1)切拼后,长方体的底面积等于原圆柱 的面积;长方体的高等于原圆柱的 。
因为:长方体的体积=底面积×高
所以:圆柱的体积= 。
(2)如果圆柱的底面半径为2厘米,高为6厘米,那么拼成的长方体的表面积是多少平方厘米?
19.(2024 垫江县)从“东方红一号”到“天绘六号”发射成功,中国空间技术研究院研制并成功发射了400个航天器,统称为“四百星”。
发射目标 第一个“百星” 第二个“百星” 第三个“百星” 第四个“百星”
完成时间(年) 41 6 3 2
我国完成“四百星”发射目标一共用了 年。观察上面统计表你有什么感受?
20.(2024 綦江区)如果小东买了这个文具盒(如图),小东与小鹏的钱数之比为2:5;如果小鹏买了这个文具盒,则小东与小鹏的钱数之比为8:13,小东原有多少钱?
21.(2024 石柱县)牛奶含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等。下面是100g牛奶中营养成分情况统计图。
(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分, 的含量最低;乳糖的含量占100g牛奶质量的 %。
(2)下面的四幅扇形统计图中,能反映条形统计图结果的是 ,请说说你选择的理由。
22.(2024 石柱县)画一画,填一填。
(1)以直线b为对称轴,画出圆的轴对称图形。
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。
(3)用数对( , )表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。
23.(2024 垫江县)某市规定:每户每月用水不超过20立方米(含20立方米)时,水费按“基本价”收费;超过20立方米时,不超过20立方米(含20立方米)部分仍按“基本价”收费;超过20立方米的部分按“调节价”收费。李老师家今年三、四月份的用水量和水费如下表所示:
月份 用水量(立方米) 水费(元)
3 15 31.5
4 23 52.8
请你算一算该市水费的“基本价格”和“调节价”分别是每立方米多少元?
(1)基本价格:
(2)调节价:
24.(2024 渝中区)甲乙丙三辆车以一定速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙,甲又比乙晚出发20分,出发后1小时40分钟追上丙,问甲出发后用了多少时间追上乙?
25.(2024 渝中区)张、王二人在银行各有一笔存款,老张存款800元,如果老张从存款中取出1/5,老王从存款中取出75%,那么老张的余款比老王的2倍还多120元.张、王二人原来共有存款多少元?
26.(2024 两江新区)小华从A到B,先下坡再上坡共用7小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?
27.(2024 彭水县)甲、乙两辆抱拉机分别耕A、B两块面积相同的土地。甲拖拉机耕了A地的;乙拖拉机耕了B地的,比甲拖拉机多耕3.6公顷。A、B两块地分别有多少公顷?(画图分析,再解答)
28.(2024 丰都县)李阿姨是一个钟点工,她的工资结算方式是每天200元,每4小时算半天,不足半天的按每小时25元结算。加班每小时30元。下面是李阿姨上周的工作情况统计。
时间 工作时长 加班时长
周一 一天 1小时
周二 4小时
周三 一天 1.5小时
周四 一天 1小时
周五 3小时
(1)李阿姨上周共工作了 个整天, 个半天,外加 个小时,另外还加班 小时。
(2)请你算一算李阿姨上周应得工资共为多少元?
29.(2024 渝中区)阅读下列材料,回答下列问题。
材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”。如65362,362﹣65=297=11×27,称65362是“网红数”。
材料二:对任意的自然数P均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),如5278=52×100+10×7+8,规定:G(P)。
(1)求证:任意两个“网红数”之和一定能被11整除;
(2)已知:s=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5),且a,b均为整数,当s+t为“网红数”时,求G(t)的最大值。
30.(2024 璧山区)育英小学六年级三个班给山区学校捐故事书,其中六(1)班捐得最多,捐了40本,六(2)班与六(3)班捐的本数的比为4:5。以下还有三条关于三个班捐书的信息,其中只有一条是正确的:
①六(1)班捐的本数占六年级三个班捐的本数的25%。
②六(1)班捐的本数与另外两个班捐的本数的比是4:9。
③六(1)班捐的本数比六年级捐的本数的多6本。
哪条信息是正确的?请你说明理由。
31.(2024 九龙坡区)如图所示是一个面积约为1040平方厘米的正六边形,空白部分是6个半径为10厘米的小扇形。求阴影部分的面积是多少平方厘米?
32.(2024 渝北区)移动公司推出一款话费套餐活动,资费标准见表:
套餐月费/元 套餐内容 被叫 套餐外资费
主叫限定时间/分钟 主叫超时费(元/分钟)
58 50 免费 0.25
88 150 0.20
118 350 0.15
说明: ①主叫:主动打电话给别人;被叫:接听别人打进来的电话。 ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟。则当月话费为58+0.25×(60﹣50)=60.5元。
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐。
(1)①小文当月的主叫时间为220分钟,则该月她的话费为 元。
②亮亮当月的主叫时间为220分钟,则该月他的话费为 元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),请用含m的代数式表示该月他们的话费差。
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是 分钟。
33.(2024 沙坪坝区)如图,ABCD是长方形,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求三角形DFG(阴影部分)的面积。
34.(2024 渝北区)有一项工程,由甲、乙、丙三个工程队每天轮流做。原计划按甲、乙、丙次序轮流做,恰好整数天完成。如果按乙、丙、甲次序轮做,比原计划多用0.5天;如果按丙、甲、乙次序做,比原计划多用天。已知甲单独做13天完成。且3个工程队的工效各不相同。这项工程由甲、乙、丙合作要多少天完工?
35.(2024 渝北区)如图,A、B是一条道路的两端点,亮亮在A点,明明在B点,两人同时出发,相向而行,他们在离A点100米的C点第一次相遇,亮亮到达B点后返回A点,明明到达A点后返回B点,两人在离B点80米的D点第二次相遇。整个过程中,两人各自的速度都保持不变,求A、B间的距离。
36.(2024 渝北区)在长方形ABCD中,AB=30cm,BC=40cm,如图P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值。
37.(2024 渝北区)底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积.
38.(2024 重庆)李师傅加工一批零件,原计划每小时加工30个,6小时可以完成,实际每小时比原计划多加工20%,实际加工这批零件比原计划提前几小时?
39.(2024 九龙坡区)甲容器中有500克20%盐水,乙容器中有500克水,先将甲中一半的盐水到入乙,充分搅拌;在将乙中一半的盐水到入甲,充分搅拌;最后将甲中盐水的一部分倒入乙,使甲、乙的盐水重量相同.求此时乙中盐水的浓度是多少?.
40.(2024 长沙)某游乐场在开门前有400人排队等待,开门后每分钟来的人数是固定的.一个入场口每分钟可以进来10个游客,如果开放4个入场口.20分钟就没有人排队,现在开放6个入口,那么开门后多少分钟后就没有人排队?
41.(2024 江北区)对于任意一个四位数m,其各位数字互不相等,若它的千位数字与百位数字的和等于十位数字与个位数字的和,则称这个四位数m为“天平数”,记F(m)为m的各个数位上的数字之和。例如:m=1432,∵1+4=3+2,∴1432是“天平数”,F(1432)=1+4+3+2=10;m=6397,∵6+3≠9+7,∴6397不是“天平数”。
(1)求出F(5234)的值;
(2)已知M,N均为“天平数”,其中M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数),N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c<9,0≤d≤9,a,b,c,d是整数)。若F(M) F(N)=264,求出满足条件的M的最大值与最小值的差。
42.(2024 石柱县)中国建筑中经常能见到如图的设计。如果图中圆的面积是6.28m2,那么整个图形中所有空白部分的面积是多少m2?(π取3.14)
43.(2024 渝北区)如图,最小正方形的边长为单位1,25个这样的小正方形拼成一个大正方形ABCD,其中,有7个最小正方形被涂上了阴影;用S表示剩下的18个最小正方形的面积和。
(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形的可能性为 ;
(2)在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边 上,距离A点 个单位长度;
(3)甲、乙两个机器人分别从A、C两点开始,同时出发绕着正方形ABCD的边行走,甲以每秒3个单位的速度顺时针行走,乙以每秒2个单位的速度逆时针行走,请计算得出:他们之间的第18次相遇在何时在何地?
44.(2024 北碚区)求图中阴影部分的周长和面积(π取3.14)
45.(2024 垫江县)1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人,如图。
(1)观察思考,发现规律:每增加1张桌子,可坐人数就增加 人。
(2)如果10张餐桌拼在一起,一共可以坐 人。
(3)按这样拼下去,m张餐桌可坐 人。(用含有字母的式子表示)
46.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
47.(2024 綦江区)六一班要举行“六一”联欢会,班干部决定买15千克水果.据调查,爱吃香蕉的同学人数和爱吃梨的同学人数的比是2:3.请你帮忙算一算,香蕉和梨分别买多少千克?
48.(2024 渝中区)加工一批零件,甲独做20天完成,乙独做每天完成这批零件的。现在两人合作完成这批零件的加工任务,甲中途休息了5天,乙也休息了若干天,这样用了19天才完成任务。求乙休息的天数?
49.(2023 两江新区)甲、乙两地相距294千米,一辆客车和一辆货车先后从两地出发,相向而行.货车先开出0.5小时后客车开出,已知货车每小时行60千米,客车的速度是货车的1.2倍.客车开出几小时后两车相遇?
50.(2024 彭水县)结合下面某乡村小学学生上学路程所用时间占比统计图,解决下列问题。
①这所小学共有学生 人。
②学生上学需要“30~60分钟”的占全班人数的 %。
③学生上学需要“90分钟以上”的有 人。
④如果小学生每分钟可走70米,学生家庭离学校最远的至少有 km。
⑤如果学生早上6:40起床,洗漱吃早餐需30分钟,你认为这所学校上午第一节课上课时间确定为 时整比较合适。
⑥教育部要求小学生睡眠应达10小时以上。你认为怎样安排晚上睡觉和早上起床时间比较合适?对于上学路程较远的同学你想对他在时间安排上做些什么提示?
51.(2024 彭水县)一种圆台形的坐凳是把圆锥上面部分去掉做成的。请计算出下面这个坐凳的体积。
重庆市小升初真题汇编:应用题
2024-2025学年六年级下册数学西师大版
参考答案与试题解析
1.(2024 渝中区)有A、B、C三种盐水,按A与B数量之比2:1混合,得到浓度为13%的盐水;按A与B的数量之比为1:2混合,得到浓度为14%的盐水。如果A、B、C数量之比为1:1:3,混合成的盐水浓度为10.2%。问:盐水C的浓度是多少?
【答案】8%。
【分析】根据“按A与B的数量之比为2:1混合”,“按A与B的数量之比1:2混合”,“按A、B、C的数量之比1:1:3混合”,从这些条件中我们发现,只要使前两次操作得到的13%的盐水与14%的盐水重量相等,就可以使13%的盐水与14%的盐水混合,得到浓度为(13%+14%)÷2=13.5%的盐水;
依据题意,这种盐水里的A和B的数量比为1:1.现在我们要用这样的盐水与盐水C按照2:3混合,得到浓度为10.2%的盐水;
因为13.5%﹣10.2%=3.3%,这样2份的13.5%的盐水就多了6.6%,这6.6%正好补全了C盐水与10.2%的盐水的差距,据此解答即可。
【解答】解:(13%+14%)÷2
=27%÷2
=13.5%
(13.5%﹣10.2%)×2
=3.3%×2
=6.6%
10.2%﹣6.6%÷3
=10.2%﹣2.2%
=8%
答:C盐水的浓度为8%。
【点评】本题考查了比的应用。
2.(2024 渝中区)一段地下管道预计15个工人每天工作4小时,18天可以完成,后来要求加快速度每天增加3人,并且每天工作时间增加1小时,那么,可以提前几天完成?
【答案】6天。
【分析】先根据“15个工人每天工作4小时,18天可以完成”计算出预计完成这项工程的总工时;再除以现在的工作时间和工人人数,即可求出现在需要的天数;用原来的天数减去现在的天数即可。
【解答】解:(4×18×15)÷(4+1)÷(15+3)
=1080÷5÷18
=216÷18
=12(天)
18﹣12=6(天)
答:可以提前6天完成。
【点评】解答本题的关键是依据工作时间,工作效率以及工作总量之间数量关系。
3.(2024 丰都县)如图是2024年我县某校三至六年级学生人数统计情况。认真读题,完成后面的问题。
(1)图中,单位“1”是 A 。
A.三至六年级学生总人数
B.五年级学生人数
(2)算一算,该校五年级学生人数占三至六年级学生总人数的 25 %。
(3)根据上面的统计图,完善下面的统计表。
年级 三年级 四年级 五年级 六年级
人数 84 100
(4)仔细思考,该校学生人数从六年级到三年级,呈现出的发展趋势是 A 。
A.逐年增长
B.逐年减少
【答案】(1)A;
(2)25;
(3)96,120;
(4)A。
【分析】(1)根据题意可知,单位“1”是三至六年级学生总人数。
(2)用“1”减去三、四、六年级的分率,即可求出五年级学生人数占三至六年级学生总人数的分率。
(3)根据百分数乘法的意义,分别求出四年级、六年级的人数即可。
(4)比较统计表中的数据即可解题。
【解答】解:(1)图中,单位“1”是A,即三至六年级学生总人数。
(2)1﹣30%﹣24%﹣21%=25%
答:该校五年级学生人数占三至六年级学生总人数的25%。
(3)84÷21%=400(人)
400×30%=120(人)
400×24%=96(人)
统计表如下:
年级 三年级 四年级 五年级 六年级
人数 84 96 100 120
(4)84<96<100<120
该校学生人数从六年级到三年级,呈现出的发展趋势是A,即逐年增长。
故答案为:A;25;96,120;A。
【点评】本题考查了根据统计表提供的信息解决实际问题的能力。
4.(2024 沙坪坝区)某商场今天卖出男、女皮衣各一件,现价都是990元,其中女式皮衣款式漂亮赚了10%,男式皮衣款式陈旧赔了10%,今天卖出这两件皮衣是赚钱还是赔钱?若是赚钱,赚了多少?若是赔钱,赔了多少?
【答案】见试题解答内容
【分析】要看是赚钱还是赔钱,需要计算后根据数字进行判断;女式皮衣,可赚10%,把原价看作单位“1”,即现价是原价的(1+10%),根据已知一个数的几分之几是多少,求这个数用除法计算得出女式皮衣的原价,然后根据一个数乘分数的意义,计算出赚的钱数;男式皮衣赔了10%,每件售价也是990元,把原价看作单位“1”,现价是原价的(1﹣10%),根据已知一个数的几分之几是多少,求这个数用除法计算得出男式皮衣的原价,然后根据一个数乘分数的意义算出赔本的钱数;然后进行比较,进而得出结论.
【解答】解:男式皮衣赔本:990÷(1﹣10%)×10%,
=1100×10%,
=110(元);
女式皮衣盈利:990÷(1+10%)×10%,
=900×10%,
=90(元);
110>90,赔钱,
110﹣90=20(元);
答:赔钱,赔20元.
【点评】此题做题时,应先判断出单位“1”,然后根据“已知一个数的几分之几是多少,求这个数用除法计算得出两种服装原价;最后根据一个数乘分数的意义,分别求出盈利的钱数和赔本的钱数,进而比较,得出结论.
5.(2024 涪陵区)有一种陀螺(如图),上半部分是圆柱,下半部分是圆锥。经过测试,当圆柱的体积与圆锥的体积之比为4:1时,陀螺会转得又稳又快。已知圆锥的底面直径是4厘米,高是1.5厘米。请你算一算,这个陀螺的体积是多少时才能使陀螺转得又稳又快?(π取3.14)
【答案】见试题解答内容
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出陀螺中圆锥部分的体积,已知圆柱的体积与圆锥的体积之比为4:1,也就是圆锥的体积相当于陀螺体积的,再根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:3.14×(4÷2)2×1.5
3.14×4×1.5
=6.28×5
=31.4(立方厘米)
答:这个陀螺的体积是31.4立方厘米时才能使陀螺转得又稳又快。
【点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
6.(2023 沙坪坝区)李师傅加工一批零件,第一天加工了48个,第二天比第一天多加工25%,第三天比第二天多加工5%,三天共完成这批零件的95%.这批零件共有多少个?
【答案】见试题解答内容
【分析】先把第一天加工的数量看成单位“1”,第二天加工的数量是第一天的1+25%,用乘法求出第二天加工的个数;
再把第二天加工的个数看成单位“1”,第三天加工的数量是第二天的1+5%,用乘法求出第三天加工的数量;
再把这批零件的总数量看成单位“1”,三天加工的数量和是总数量的95%,求总数量用除法.
【解答】解:48×(1+25%),
=48×125%,
=60(个);
60×(1+5%),
=60×105%,
=63(个);
(48+60+63)÷95%,
=171÷95%,
=180(个);
答:这批零件共有180个.
【点评】解答此题的关键是分清这几个单位“1”的区别,求单位“1”的百分之几用乘法;已知单位“1”的百分之几是多少,求单位“1”用除法.
7.(2017 白银)如图所示,AB=12厘米,ED=DA=6厘米,小虫P从A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.
(1)小虫P从A点出发几秒后,三角形APE是等腰直角三角形?
(2)当小虫P到达C时,另一只小虫Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①小虫Q从A点出发几秒后,四边形AQPE是梯形?
②当∠QPD=45度时,四边形AQPE的面积是多少平方厘米?
【答案】见试题解答内容
【分析】(1)由图可知:当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;然后求出A点到B点的距离及A点到CD中点的距离,进而根据:路程÷速度=时间,分别解答即可;
(2)①当DP∥AQ时,AQPE就是梯形,可设小虫Q从A点出发x秒后四边形AQPE是梯形,列式为12﹣x=2x,解答即可.
②当∠QPD=45°时,PF=6cm,PC+AQ=6cm.又因为小虫Q 的速度是小虫P 的2倍,所以小虫Q 行驶路程也是小虫P 的2倍,AQ=64cm,r然后将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积,进一步解答即可.
【解答】解:(1)如图:
当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,
需要:12÷1=12(秒);
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,
需要:(12+6+6)÷1
=24÷1
=24(秒);
答:小虫P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形.
(2)①如图:
可设小虫Q从A点出发x秒后四边形AQPE是梯形,
12﹣x=2x
3x=12
x=4
答:小虫Q从A点出发4秒后,四边形AQPE是梯形.
②如图:
图中小虫Q从A 点向上运动,小虫P 同时从C 点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm.又因为小虫Q 的速度是小虫P 的2倍,所以小虫Q 行驶路程也是小虫P 的2倍,AQ=64cm.而四边形AQPE 为四边形,可以将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积是(4+10)×6÷2=42cm2,6×10÷2=30cm2,所以四边形面积为72 cm2.
【点评】明确当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;是解答此题的关键.解决本题我们运用了等腰直角三角形的知识、梯形的性质及行程问题的基本数量关系,运用了转化的解题策略,还运用了分情况全面考虑问题的方法.
8.(2024 渝北区)一个水果商从外地运回2000千克苹果,进价是每千克4元,运费及其他支出是1000元.售完这批水果要损耗25%.
(1)如果要不亏本,每千克苹果至少应卖多少元?
(2)如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利多少元?
【答案】见试题解答内容
【分析】(1)先用总重量乘每千克的进价是总进价,然后再加上运费就是成本价;进而把运进苹果的总重量看成单位“1”,售出的苹果重量为苹果总重量的(1﹣25%),由此求出实际售出的苹果重量;然后根据:总价÷数量=单价,即可求出每千克苹果至少应卖的单价;
(2)先求出实际售出的苹果重量,然后乘单价,求出实际卖到的总钱数,然后减去成本价,即可求出盈利的钱数.
【解答】(1)(4×2000+1000)÷[2000×(1﹣25%)]
=9000÷1500
=6(元)
答:如果要不亏本,每千克苹果至少应卖6元.
(2)7×2000×(1﹣25%)﹣(4×2000+1000)
=10500﹣9000
=1500(元)
答:如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利1500元.
【点评】解答此题的关键是:认真分析题意,明确题中数量间的基本关系,然后根据单价、数量和总价三者之间的关系,进行解答.
9.(2024 沙坪坝区)有一些相同的房间需要粉刷一天,4名师傅去粉刷8个房间,结果其中有40平方米的墙面未来得及刷;同样的时间6名徒弟刷9个房间的墙面。每名师傅比徒弟一天多刷20平方米的墙面。
(1)求每个房间需要粉刷的墙面面积。
(2)某老板现有40个这样的房间需要粉刷,若请3名师傅带3名徒弟去,需要几天完成?
(3)已知每名师傅、每名徒弟每天的工资分别是85元、65元,老板要求在3天内完成40个房间的粉刷任务。问:如何在10个人以内雇佣人员最合算?最低费用是多少?(10人不一定全部雇佣)
【答案】(1)60平方米;(2)4天;(3)1755元。
【分析】(1)根据题意可得等量关系:每名师傅每天粉刷的面积﹣每名徒弟每天粉刷的面积=每名师傅比徒弟一天多刷的面积,其中每名师傅每天粉刷的面积,每名徒弟每天粉刷墙面的面积,据此列出方程,并求解。
(2)由上一题分别求出每名师傅、每名徒弟每天粉刷的面积,然后用总面积除以3名师傅和3名徒弟每天粉刷的面积和,即可求出所需的天数。
(3)先求出3天完成粉刷40个这样的房间,每天需粉刷的面积,再根据师傅和徒弟每天粉刷的面积,考虑几种雇佣人员的情况,分别计算出每种情况的花费,比较后得出结论,并计算出最低花费。
【解答】解:(1)设每个房间需要粉刷的墙面面积是x平方米。
20
1212=20×12
3(8x﹣40)﹣18x=240
24x﹣120﹣18x=240
6x﹣120=240
6x﹣120+120=240+120
6x=360
6x÷6=360÷6
x=60
答:每个房间需要粉刷的墙面面积是60平方米。
(2)每名师傅每天粉刷墙面的面积为:
=110(平方米)
每名徒弟每天粉刷墙面的面积为:110﹣20=90(平方米)
40个这样的房间粉刷墙面需用时:
(40×60)÷(110×3+90×3)
=2400÷(330+270)
=2400÷600
=4(天)
答:需要4天完成。
(3)40个这样的房间3天完成粉刷,每天需粉刷的面积:
40×60÷3
=2400÷3
=800(平方米)
情况一:全部雇佣徒弟粉刷,需要人数:
800÷90=8(名)……80(平方米)
徒弟需:8+1=9(人)
一天的费用:65×9=585(元)
情况二:雇佣4名师傅,还需徒弟:
(800﹣110×4)÷90
=(800﹣440)÷90
=360÷90
=4(名)
一天的费用:
85×4+65×4
=340+260
=600(元)
情况三:全部雇佣师傅粉刷,需要人数:
800÷110=7(名)……30(平方米)
师傅需:7+1=8(人)
一天的费用:85×8=680(元)
585<600<680
雇佣9名徒弟粉刷3天的费用:
585×3=1755(元)
答:雇佣9名徒弟粉刷最合算,最低费用是1755元。
【点评】(1)考查列方程解决问题,从题目中找出等量关系,按等量关系列出方程。
(2)求出每名师傅和每名徒弟的工作效率是解题本题的关键。
(3)先求出每天规定的工作量,再安排方案,根据每天的花费找出最佳方案。
10.(2024 渝北区)六年级小语种选修班开课了。第一周参加日语班的男生比女生多10人,第二周参加日语班的男生比第一周少,参加日语班的女生比第一周多,第二周参加日语班课的男生和女生一共有59人,问第一周参加日语班学习的男生和女生各有多少人?
【答案】40人,30人。
【分析】设第一周参加日语班的女生有x人,则男生有(10+x)人;第二周参加日语班的男生有(10+x)×(1),第二周参加日语班的女生有(1)x人,合起来其共59人。根据这个等量关系列方程解答。
【解答】解:设第一周参加日语班的女生有x人,则男生有(10+x)人。
(10+x)×(1)+(1)x=59
6xx=59
6x﹣6=59﹣6
x53
x=30
当x=30时,10+x=10+30=40
答:第一周参加日语班学习的男生有40人,女生有30人。
【点评】列方程解决问题的关键是准确分析题目中的等量关系。
11.(2022 凤凰县)市政府要求地铁集团过江隧道工程12个月完工.现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元.由于前期工程路面较宽,可由甲、乙两队共同施工.随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对中山大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
(1)求两套方案中m和n的值;
(2)通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
【答案】见试题解答内容
【分析】(1)由于甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成,所以甲做了12个月,乙做了m个月,则甲完成了全部的12,乙完成了全部的m,由此可得:12m=1.由于由②可得:.进而解方程求出m=6,n=8.
(2)方案①需要资金12×600+6×400=9600万元,方案②需要资金400×12+600×8=9600万元,即两种方案所需资金相同,由于方案①合作时间较短,对交通影响较小,所以应选择方案①.
【解答】解:(1)
m=1
m
m=6
n=1
n
n=8.
答:方案①中两队合作6天,方案②中两队合作8天.
(2)方案①需要资金12×600+6×400=9600万元,
方案②需要资金400×12+600×8=9600万元,
即两种方案所需资金相同.
由于方案①合作时间较短,对交通影响较小,所以应选择方案①.
【点评】完成本题要注意分析所给条件,然后根据工作效率、工作时间及工作量之间的关系列出方程解答.
12.(2024 九龙坡区)(附加题).右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状,请你计算出它的体积.
【答案】见试题解答内容
【分析】可以把这个组合形体看成两部分,上面是圆柱的一半,下面是圆柱,它们的体积之和即是这个物体的体积.
【解答】解;7﹣5=2( 厘米),
3.14×32×2÷2=28.26(立方厘米),
3.14×32×5=141.3(立方厘米),
28.26+141.3=169.56(立方厘米),
答:它的体积是169.56立方厘米.
【点评】此题主要考查圆柱的体积公式及其计算.
13.(2024 九龙坡区)实验小学举行庆“六一”男女大合唱,原计划合唱队中女生人数占合唱队总人数的,后来考虑到合唱效果,将增加5名男生,这时女生与男生人数的比是6:5.合唱队原有女生多少名?
【答案】见试题解答内容
【分析】原计划合唱队中女生人数占合唱队总人数的,则男生是女生的(1),男生增加5名后,男生是女生的,则这5名男生占女生人数的,根据分数除法的意义,用5人除以()就是原有女生人数.
【解答】解:原来男生是女生的:
(1)
则合唱队原有女生:
5÷()
=5
=30(人)
答:合唱队原有女生30人.
【点评】明确这一过程中,女生人数没有发生变化,从而根据男生占女生人数分率的变化求出女生有多少人是完成本题的关键.
14.(2024 石柱县)如图是小伟跳远时留下的脚印。如果你是裁判员,该怎样测量他的成绩?请在图中画出待测量的线段。
【答案】
【分析】此题为数学知识的应用,由实际出发,老师测量跳远成绩的依据是垂线段最短,即测量后脚印与起跳线间的垂直距离即为跳远成绩。
【解答】解:如图:
【点评】此题考查知识点垂线段最短。
15.(2024 渝北区)如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm.由此可得到木棒长为 5 cm。
(2)由题(1)的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年才出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁?
【答案】见试题解答内容
【分析】(1)根据题意并结合题图,我们可轻松得到:从刻度5到刻度20之间的线段长度正好是这根木棒长度的3倍.据此即可求出答案.
(2)此题中爷孙俩的年龄差就相当于上题中的木棒长度,这样即可轻松求出他们的年龄差为:(125+40)÷3=55岁.再结合“你若是我现在这么大,我已经125岁”便可求出爷爷现在的年龄.
【解答】解:(1)20﹣5=15(cm)
15÷3=5(cm)
答:木棒长为5cm.
(2)125+40=165(岁)
165÷3=55(岁)
125﹣55=70(岁)
答:爷爷现在70岁.
【点评】解答此题的关键是,理解木棒长度与两个刻度之间长度的关系即可轻松作答.
16.(2024 渝北区)百舸竞渡,激情飞扬。为纪念爱国诗人屈原,某市举行了龙舟赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间关系的图像,请你根据图像回答下列问题:
(1)1.8分钟时,龙舟 甲 队处于领先地位,在这次龙舟比赛中,龙舟 乙 队先到达终点。
(2)求先到达终点的龙舟队在比赛开始多少分钟后开始领先。
【答案】(1)甲,乙;(2)3.4分。
【分析】(1)根据图示可知,甲、乙两支龙舟队出发后,甲队在2.2分钟前一直处于领先位置,但最后乙队用时3.8分到达目的地,甲队用时4分钟到达目的地,即乙队先到达终点;
(2)根据图示可知,甲队从出发到到达终点处于匀速运动,速度一直没有变化,根据“速度=路程÷时间”求出甲龙舟队的划行速度;根据“路程=速度×时间”求出甲队在2.2分时划行的路程,根据图示可知,2.2分时乙队划行了400米,两者作差即可求出2.2分时甲队和乙队的路程差;根据图示可知,从2.2分开始,乙队开始加速,根据图示可知,乙队从2.2分到到达终点的3.8分共用时(3.8﹣2.2)时间内共划行了(1000﹣400)米,根据“速度=路程÷时间”求出乙队从2.2分开始时的速度;根据“追及时间=路程差÷速度差”求出乙队追上甲队的用时,用乙队开始加速时的时间2.2分加上追及时间即是乙队领先的时间,据此解答。
【解答】解:(1)1.8分钟时,龙舟甲队处于领先地位,在这次龙舟比赛中,龙舟乙队先到达终点。
(2)甲队的速度:1000÷4=250(米/分)
2.2分时甲队划行路程:2.2×250=550(米)
2.2分时甲、乙队划行路程差:550﹣400=150(米)
2.2分到3.8分乙队的速度:(1000﹣400)÷(3.8﹣2.2)=375(米/分)
乙队追上甲队的用时:150÷(375﹣250)=1.2(分)
乙队追上甲队的时间:2.2+1.2=3.4(分)
答:先到达终点的龙舟队在比赛开始3.4分钟后开始领先。
【点评】本题考查了行程问题的应用以及学生能读懂统计图并根据统计图解决问题的能力。
17.(2024 北碚区)给定一个十进制下的自然数n,对于n每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数n的“模二数”,记为M2(n)。如M2(975)=111,M2(385)=101,M2(476)=010,对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1。如975、385的“模二数”111、101相加的运算过程如图所示。
根据以上材料,解决下列问题:
(1)M2(9342)的值为 1100 ,M2(59)+M2(9342)的值为 1111 。
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数为“模二相加不变”。
①判断16与45是否“模二相加不变”,并说明理由。
②与45互为“模二相加不变”的两位数共有 30 个。
【答案】(1)1100,1111;(2)①否,因为16和45的和的“模二数”与它们的“模二数”的和不相等;②30。
【分析】(1)根据“模二数”的定义,直接计算M2(9342),M2(59)即可;然后再根据“模二数”的加法规定计算M2(59)+M2(9342)即可;
(2)①根据两个数为“模二相加不变”的定义,计算M2(16+45)与M2(16)+M2(45)是否相等即可判断;
②根据模二结果数分别为10、11、01、00分别讨论即可找出和45互为“模二相加不变”的两位数。
【解答】解:(1)M2(9342)的值为1100
M2(59)+M2(9342)
=11+1100
=1111
即M2(59)+M2(9342)的值为1111。
(2)①M2(16+45)=M2(61)=01
M2(16)+M2(45)=10+01=11
即16和45的和的“模二数”与它们的“模二数”的和不相等,即这两个数不是“模二相加不变”。
②M2(45)=01
模二结果是10的两位数有:12,32,52,72,92,14,34,54,74,94,16,36,56,76,96,18,38,58,78,98,10,30,50,70,90,共计25个;
10+01=11
即满足题意的模二结果是10的两位数有:12,32,52,14,34,54,10,30,50,共计9个两位数满足题意。
模二结果是11的两位数有:11,31,51,71,91,13,33,53,73,93,15,35,55,75,95,17,37,57,77,97,19,39,59,79,99,共计25个;
11+01=100
即满足题意的模二结果是11的两位数有:55,75,95,57,77,97,59,79,99,共计9个两位数满足题意。
模二结果是01的两位数有:21,23,25,27,29,41,43,45,47,49,61,63,65,67,69,81,83,85,87,89,共计20个;
01+01=10
即满足题意的模二结果是01的两位数有:25,27,29,45,47,49,共计6个两位数满足题意。
模二结果是00的两位数有:20,22,24,26,28,40,42,44,46,48,60,62,64,66,68,80,82,84,86,88,共计20个;
00+01=01
即满足题意的模二结果是00的两位数有:20,22,24,40,42,44,共计6个两位数满足题意。
所以与45互为“模二相加不变”的两位数共有:9+9+6+6=30(个)
答:与45互为“模二相加不变”的两位数共有30个。
故答案为:(1)1100,1111;(2)②30。
【点评】本题考查了定义新运算的应用,数字的变化规律的应用,理解定义内容,能将定义与已学内容相结合是解题的关键。
18.(2024 垫江县)推导圆柱的体积。
将圆柱如图切分后拼成一个近似的长方体。切拼前后,圆柱的体积没有发生改变,表面积增加了。
(1)切拼后,长方体的底面积等于原圆柱 底面 的面积;长方体的高等于原圆柱的 高 。
因为:长方体的体积=底面积×高
所以:圆柱的体积= 底面积×高 。
(2)如果圆柱的底面半径为2厘米,高为6厘米,那么拼成的长方体的表面积是多少平方厘米?
【答案】(1)底面,高,底面积×高;
(2)124.48平方厘米。
【分析】(1)根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后体积不变,表面积增加了,拼成的长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,根据长方体的体积公式推导出圆柱的体积公式。
(2)拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,根据圆柱的表面积=侧面积+底面积×2,长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)切拼后,拼成的长方体的底面积等于原圆柱的底面积,长方体的高等于原圆柱的高。
因为长方体的体积=底面积×高,
所以圆柱的体积=底面积×高。
(2)2×3.14×2×6+3.14×22×2+6×2×2
=12.56×6+3.14×4×2+12×2
=75.36+25.12+24
=124.48(平方厘米)
答:拼成的长方体的表面积是124.48平方厘米。
故答案为:底面,高,底面积×高。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用,圆柱的表面积公式、长方体的表面积公式及应用。
19.(2024 垫江县)从“东方红一号”到“天绘六号”发射成功,中国空间技术研究院研制并成功发射了400个航天器,统称为“四百星”。
发射目标 第一个“百星” 第二个“百星” 第三个“百星” 第四个“百星”
完成时间(年) 41 6 3 2
我国完成“四百星”发射目标一共用了 52 年。观察上面统计表你有什么感受?
【答案】52;中国空间技术研究院研制“四百星”时间用的越来越少。(答案不唯一)
【分析】把4个数字相加,就是我国完成“四百星”发射目标一共用了多少年;感受:根据完成时间的长短解答即可。
【解答】解:41+6+3+2
=47+3+2
=50+2
=52(年)
答:我国完成“四百星”发射目标一共用了52年。
41>6>3>2
发现:中国空间技术研究院研制“四百星”时间用的越来越少。(答案不唯一)
故答案为:52。
【点评】熟练掌握整数加减法和比较大小的方法是解答本题的关键。
20.(2024 綦江区)如果小东买了这个文具盒(如图),小东与小鹏的钱数之比为2:5;如果小鹏买了这个文具盒,则小东与小鹏的钱数之比为8:13,小东原有多少钱?
【答案】20元。
【分析】由题意可知:小东和小鹏剩余的钱数的是不变的,把二人剩余的钱数看作单位“1”,则小东买了这个文具盒后,他剩余的钱数占总剩余钱数的,当小鹏买了这个文具盒后,小东的钱数,占总剩余钱数的,增加了(),增加的分率所对应的量是5元,于是用对应量5除以对应分率(),就得到二人剩余钱数的总量,进而根据求一个数的几分之几是多少,用乘法即可求解。
【解答】解:5÷()
=5÷()
=5
=52.5
=20(元)
答:小东原来有20元钱。
【点评】解答此题的关键是:先求出5元所对应的剩余钱数总量的几分之几,从而可以求出剩余的总钱数,进而求出小东原来的钱数。
21.(2024 石柱县)牛奶含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等。下面是100g牛奶中营养成分情况统计图。
(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分, 其它营养成分 的含量最低;乳糖的含量占100g牛奶质量的 4.9 %。
(2)下面的四幅扇形统计图中,能反映条形统计图结果的是 B ,请说说你选择的理由。
【答案】(1)其它营养成分,4.9,(2)B,我的理由是蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意,B图符合题意。
【分析】(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分,其它营养成分的含量最低。用乳糖的含量除以100克就得乳糖的占比。
(2)蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意。
【解答】解:(1)4.9÷100=4.9%
答:观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分,其它营养成分的含量最低;乳糖的含量占100g牛奶质量的4.9%。
(2)四幅扇形统计图中,能反映条形统计图结果的是B。我的理由是蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意,B图符合题意。
故答案为:其它营养成分,4.9,B。
【点评】本题考查了学生对数据的掌握及从统计图中获取信息的能力。
22.(2024 石柱县)画一画,填一填。
(1)以直线b为对称轴,画出圆的轴对称图形。
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。
(3)用数对( 2 , 3 )表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。
【答案】(1)(2)(3),2,3。
【分析】(1)根据轴对称图形的画法,以直线b为对称轴,在对称轴的右面画出圆的轴对称图形即可。
(2)根据图形旋转的方法,点P拨动,画出三角形先绕点P逆时针旋转90°后的图形,形状不变,并标注“①”,再根据图形平移的方法,画出图形①向上平移4格后的图形即可。
(3)用数对(2,3)表示点M的位置;根据图形缩小的方法,按1:3的比画出长方形缩小到原来后的图形,并标注“②”即可。
【解答】解:(1)以直线b为对称轴,画出圆的轴对称图形。如图:
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。如图:
(3)用数对(2,3)表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。如图:
故答案为:2,3。
【点评】本题考查了轴对称图形、图形的旋转、平移、图形的缩小以及数对表示位置知识,结合题意分析解答即可。
23.(2024 垫江县)某市规定:每户每月用水不超过20立方米(含20立方米)时,水费按“基本价”收费;超过20立方米时,不超过20立方米(含20立方米)部分仍按“基本价”收费;超过20立方米的部分按“调节价”收费。李老师家今年三、四月份的用水量和水费如下表所示:
月份 用水量(立方米) 水费(元)
3 15 31.5
4 23 52.8
请你算一算该市水费的“基本价格”和“调节价”分别是每立方米多少元?
(1)基本价格:
(2)调节价:
【答案】(1)2.1元;(2)3.6元。
【分析】(1)3月份的用水量为15立方米,不超过20立方米(含20立方米),水费除以用水量可得”基本价格“,据此作答即可。
(2)4月份的用水量为23立方米,超过20立方米(含20立方米),水费总额先减去20立方米乘“基本价格”的结果,余额除以超过20立方米的用水量,可得”调节价“,据此作答即可。
【解答】解:(1)31.5÷15=2.1(元)
答:该市水费的“基本价格”是每立方米2.1元。
(2)(52.8﹣2.1×20)÷(23﹣20)
=(52.8﹣42)÷3
=10.8÷3
=3.6(元)
答:该市水费的“调节价”是每立方米3.6元。
【点评】本题考查了整数、小数混合运算的应用问题。
24.(2024 渝中区)甲乙丙三辆车以一定速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙,甲又比乙晚出发20分,出发后1小时40分钟追上丙,问甲出发后用了多少时间追上乙?
【答案】见试题解答内容
【分析】根据已知条件得知,乙用40分钟所走的距离与丙用50分钟所走的距离相等,所以丙的速度是乙的;甲用100分钟所走的距离与丙用130分钟所走的距离相等.故丙用130分钟所走的距离,乙用了:130104(分钟),即甲用100分钟走的距离,乙用104分钟走完.由于甲比乙晚出发20分钟,当甲追上乙时,设甲用了x分钟,则乙用了(x+20)分钟,由此可得方程:.
【解答】解:丙用130分钟所走的距离,乙用了:
130104(分钟),
设甲用了x分钟,可得:
,
104x=100(x+20),
104x=100x+2000,
4x=2000,
x=500.
答:甲出发后需要500分钟才能追上乙.
【点评】首先根据行驶相同的距离、所用时间与速度成反比求出他们的速度比是完成本题的关键.
25.(2024 渝中区)张、王二人在银行各有一笔存款,老张存款800元,如果老张从存款中取出1/5,老王从存款中取出75%,那么老张的余款比老王的2倍还多120元.张、王二人原来共有存款多少元?
【答案】见试题解答内容
【分析】先把老张原来的存款钱数看成单位“1”,余下的钱数是总钱数的(1),由此用乘法求出剩下的钱数;再根据老张的余款比老王的2倍还多120元,求出老王剩下的钱数;然后把乙原来的存款钱数看成单位“1”,剩下的钱数是它的(1﹣75%),由此用除法求出老王原来的存款钱数,据此再把他们的钱数加起来即可.
【解答】解:老张剩下的钱数是:800×(1)=640(元),
则老王剩下的钱数是:(640﹣120)÷2,
=520÷2,
=260(元),
所以老王的存款是:260÷(1﹣75%),
=260÷25%,
=1040(元),
1040+800=1840(元),
答:二人原来共有1840元存款.
【点评】解答此题的关键是分清两个单位“1”的区别,再根据二人的余款关系进行求解.
26.(2024 两江新区)小华从A到B,先下坡再上坡共用7小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?
【答案】见试题解答内容
【分析】方法1:①要求原路返回所用的时间,需要求出,上坡路的距离和下坡路的距离分别是多少;所以这里可以根据题干先求出去时的上坡路程和下坡路程;
②根据题干,设小华从A到B上坡路程为x千米,则下坡路程为(24﹣x)千米,根据速度、时间和路程的关系,利用上坡路用的时间+下坡路用的时间=总时间,即可列出方程求得去时的上坡路程和下坡路程,从而得出返回时的上坡路程和下坡路程,即可解决问题;
方法2:去时上坡就是回来时的下坡,去时下坡就是回来时上坡,由此可知全程上坡24千米,下坡24千米,所以全程用时24÷4+24÷3=14(小时),减去去时用时即可求解.
【解答】解:方法1:设小华从A到B上坡路程为x千米,则下坡路程为24﹣x千米,根据题意可得方程:
7
4x+72﹣3x=2×43
x=14,
24﹣14=10(千米),
那么可得返回时上坡路为10千米,下坡路为14千米:
,
(小时),
方法2:24÷4+24÷3
=6+8
=14(小时),
14﹣7(小时).
答:返回时用的时间是小时.
【点评】此题考查了速度、时间和路程之间的关系的灵活应用,这里抓住来回时,上坡和下坡的路程正好相反,是解决本题的关键.
27.(2024 彭水县)甲、乙两辆抱拉机分别耕A、B两块面积相同的土地。甲拖拉机耕了A地的;乙拖拉机耕了B地的,比甲拖拉机多耕3.6公顷。A、B两块地分别有多少公顷?(画图分析,再解答)
【答案】;21公顷。
【分析】根据题意可知A、B两块面积相同,把A地面积看作单位“1”,平均分成5份,其中的2份就是甲拖拉机耕的面积;把B地面积看作单位“1”,平均分成7份,其中的4份就是乙拖拉机耕的面积;乙拖拉机比甲拖拉机多耕3.6公顷;据此画出线段图;乙拖拉机比甲拖拉机多耕了单位“1”的(),对应的数量是3.6公顷,然后再用3.6除以()即可。
【解答】解:画图如下:
3.6÷()
=3.6
=21(公顷)
答:A、B两块地分别有21公顷。
【点评】本题关键是根据题意画出线段图,弄清数量关系,然后再列式解答。
28.(2024 丰都县)李阿姨是一个钟点工,她的工资结算方式是每天200元,每4小时算半天,不足半天的按每小时25元结算。加班每小时30元。下面是李阿姨上周的工作情况统计。
时间 工作时长 加班时长
周一 一天 1小时
周二 4小时
周三 一天 1.5小时
周四 一天 1小时
周五 3小时
(1)李阿姨上周共工作了 3 个整天, 1 个半天,外加 3 个小时,另外还加班 3.5 小时。
(2)请你算一算李阿姨上周应得工资共为多少元?
【答案】(1)3,1,3,3.5;
(2)880元。
【分析】(1)根据统计表中的数据,按照李阿姨的工资结算方式,数出时间完成填空;
(2)根据单价×数量=总价,分别计算每天、半天、加班的工资,再求和即可。
【解答】解:(1)李阿姨上周共工作了3个整天,1个半天,外加3个小时,另外还加班3.5小时。
(2)3×200+25×(4+3)+30×3.5
=600+175+105
=880(元)
答:李阿姨上周应得工资共为880元。
故答案为:3,1,3,3.5。
【点评】本题考查了根据统计表提供的信息解决实际问题的能力。
29.(2024 渝中区)阅读下列材料,回答下列问题。
材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”。如65362,362﹣65=297=11×27,称65362是“网红数”。
材料二:对任意的自然数P均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),如5278=52×100+10×7+8,规定:G(P)。
(1)求证:任意两个“网红数”之和一定能被11整除;
(2)已知:s=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5),且a,b均为整数,当s+t为“网红数”时,求G(t)的最大值。
【答案】(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数),
根据“网红数”的特征可知:n﹣m=1lk,b﹣a=1lh(或m﹣n=11k,a﹣b=11h),
所以n=11k+m,b=11h+a
所以
=1000m+n+1000a+b
=1000m+11k+m+1000a+11h+a
=1001m+1001a+11(k+h)
=11(91m+9la+k+h)
因为m、a、k、h都是整数,
所以91m+91n+h+k为整数,
所以任意两个“网红数”之和一定能被11整除。
(2)。
【分析】(1)根据题意,设出两个“网红数”,根据“网红数”的特征:末三位表示的数与末三位之前的数字表示的数之差是11的倍数,即把这两个“网红数”分别用后三位和后三位前面的数作差后表示为11的倍数,然后再用位值原理把两个“网红数”表示出来后写成11的倍数的形式即可证明;
(2)根据题意,s+t=300+10b+a+1000b+100a+1142=1010b+101a+1442,根据1≤a≤5或6≤a≤7,因为s+t为“网红数”,则s+t可以表示为末三位表示的数与末三位之前的数字表示的数之差是11的倍数,即该差能被11整除,利用能被11整除的特征分析解答即可求出不同的t值,再把t表示为100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),根据G(t)。分别求出G(t)的值,然后比较大小,找出最大的即可解答本题。
【解答】解:(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数),
根据“网红数”的特征可知:n﹣m=1lk,b﹣a=1lh(或m﹣n=11k,a﹣b=11h),
即n=11k+m,b=11h+a
又
=1000m+n+1000a+b
=1000m+11k+m+1000a+11h+a
=1001m+1001a+11(k+h)
=11(91m+9la+k+h)
因为m、a、k、h都是整数,
所以91m+91n+h+k为整数,
所以11(91m+9la+k+h)是11的倍数,
即一定能被11整除。
所以任意两个“网红数”之和一定能被11整除。
(2)①当1≤a≤5时,
因为s=300+10b+a,t=1000b+100a+1142
所以s+t=(300+10b+a)+(1000b+100a+1142)
=1010b+101a+1442
=1000b+10b+100a+a+1000+400+40+2
=(1000b+1000)+(100a+400)+(10b+40)+(a+2)=1000(b+1)+100(a+4)+10(b+4)+(a+2)
因为s+t为“网红数”,
根据“网红数”的特征可知:(b+1)能被11整除,
即100(a+4)+10(b+4)+(a+2)﹣(b+1)能被11整除,
所以101a+9b+441=11×9a+2a+11b﹣2b+11×40+1=11×(9a﹣2b+40)+(2a﹣2b+1)能被11整除,
因为11×(9a﹣2b+40)能被11整除,
所以只需2a﹣2b+1能被11整除即可,
因为l≤a≤5,0≤b≤5,
所以﹣7≤2a﹣2b+1≤11,
所以2a﹣2b+1=0或11,
此时a=5,b=0,
此时t=1000(b+1)+100(a+1)+4×10+2=1000×(0+1)+100×(5+1)+4×10+2=1642=100×16+10×4+2,
所以G(t)=G(1642)17.07,
②当6≤a≤7时,
因为s=300+10b+a,t=1000b+100a+1142
所以s+t=(300+10b+a)+(1000b+100a+1142)
=1010b+101a+1442
=1000b+10b+100a+a+2000﹣600+40+2
=(1000b+2000)+(100a﹣600)+(10b+40)+(a+2)=1000(b+2)+100(a﹣6)+10(b+4)+(a+2)
因为s+t为“网红数”,
根据“网红数”的特征可知:(b+2)能被11整除,
即100(a﹣6)+10(b+4)+(a+2)﹣(b+2)能被11整除,
所以101a+9b﹣560=11×9a+2a+11b﹣2b﹣11×51+1=11×(9a﹣2b﹣51)+(2a﹣2b+1)能被11整除,
因为11×(9a﹣2b﹣51)能被11整除,
所以只需2a﹣2b+1能被11整除即可,
因为6≤a≤7,0≤b≤5,
所以3≤2a﹣2b+1≤15,
所以2a﹣2b+1=11,
此时a=6,b=1或a=7,b=2,
当a=6,b=1,t=1000(b+1)+100(a+1)+4×10+2=1000×(1+1)+100×(6+1)+4×10+2=2742=100×27+10×4+2,
G(t)=G(2742)28.04,
当a=7,b=2,t=1000(b+1)+100(a+1)+4×10+2=1000×(2+1)+100×(7+1)+4×10+2=3842=100×38+10×4+2,
G(t)=G(3842)39.03,
因为17.07<28.04<39.03,所以G(t)max。
答:G(t)的最大值是。
【点评】本题考查了能被11整除的数的应用以及定义新运算是最值问题的应用,理解题意,从题目中获取信息,列出正确的代数式,再由数的特点求解是解题的关键。
30.(2024 璧山区)育英小学六年级三个班给山区学校捐故事书,其中六(1)班捐得最多,捐了40本,六(2)班与六(3)班捐的本数的比为4:5。以下还有三条关于三个班捐书的信息,其中只有一条是正确的:
①六(1)班捐的本数占六年级三个班捐的本数的25%。
②六(1)班捐的本数与另外两个班捐的本数的比是4:9。
③六(1)班捐的本数比六年级捐的本数的多6本。
哪条信息是正确的?请你说明理由。
【答案】③;六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【分析】①六(1)班捐的本数已知,六(2)、六(3)班捐的本数比已知,如果再告诉六(1)班捐的本数所占的分率或六年级三个个班捐的总本数,才能求出六(1)班捐的本数占六年级三个班捐的本数百分之几。
②同理,无法求出六(1)班捐的本数与另外两个班捐的本数的比。
③六(1)班捐的本数比六年级捐的本数的多6本,六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【解答】解:“六(1)班捐的本数比六年级捐的本数的多6本”是正确的。
理由:六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【点评】六(1)班与六(2)班、六(3)班捐的本数没有任何联系,无法求出六(1)班捐的本数占六年级三个班总本数的百分之几或六(1)本捐的本数与另外两个班捐的本数之比。
31.(2024 九龙坡区)如图所示是一个面积约为1040平方厘米的正六边形,空白部分是6个半径为10厘米的小扇形。求阴影部分的面积是多少平方厘米?
【答案】412平方厘米。
【分析】由图意可知:所要求的阴影面积=正六边形的面积﹣六个小扇形面积;正六边形的面积已知,现在关键是求小扇形的面积,由扇形面积公式S可知,只需要求出半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么∠AOC=120°,又知四边形ABCD是平行四边形,所以∠ABC=120°,再根据半径为10厘米,求出扇形的面积;从而可以求得阴影部分的面积。
【解答】解:因为正六边形每边所对圆心角为60°,那么∠AOC=120°;
又知四边形ABCO是平行四边形,所以∠ABC=120°。
阴影部分的面积:10403.14×102×6
=10403.14×100×6
=1040﹣628
=412(平方厘米)
答:阴影部分的面积是412平方厘米。
【点评】解答此题的关键是明白:阴影面积是用正六边形的面积减去六个小扇形面积。
32.(2024 渝北区)移动公司推出一款话费套餐活动,资费标准见表:
套餐月费/元 套餐内容 被叫 套餐外资费
主叫限定时间/分钟 主叫超时费(元/分钟)
58 50 免费 0.25
88 150 0.20
118 350 0.15
说明: ①主叫:主动打电话给别人;被叫:接听别人打进来的电话。 ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟。则当月话费为58+0.25×(60﹣50)=60.5元。
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐。
(1)①小文当月的主叫时间为220分钟,则该月她的话费为 102 元。
②亮亮当月的主叫时间为220分钟,则该月他的话费为 118 元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),请用含m的代数式表示该月他们的话费差。
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是 300 分钟。
【答案】(1)102,118;
(2)(0.05m+12.5)元;
(3)300。
【分析】(1)①小文办理的是月使用费为88元的套餐,主叫时间为150分钟,小文当月的主叫时间为220分钟,超过150分钟每分钟收费0.2元,根据分段计费的方法解答;
②亮亮办理的是月使用费为118元的套餐,主叫时间为350分钟,亮亮当月的主叫时间为220分钟,没有超过规定的时间,所以亮亮该月话费为118元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),因为m>350分钟,所以两人的话费均有套餐费和主叫超时费两部分组成,根据具体数据列式即可。
(3)由题意可知,小文和亮亮11月的话费都是118元,则小文的主叫时间为50+(118﹣58)÷0.25,据此解答即可。
【解答】解:(1)①88+0.2×(220﹣150)
88+0.2×70
=88+14
=102(元)
答:小文该月话费为102元。
②亮亮当月的主叫时间为220分钟,220分钟<350分钟。
答:亮亮该月他的话费为118元。
(2)小文该月话费为:88+0.2×(m﹣50)
=88+0.2m﹣10
=0.2m+78(元);
亮亮该月话费为:
188+0.15×(m﹣350)
=188+0.15m﹣52.5
=0.15m+65.5(元);
他们的话费差为(0.2m+78)﹣(0.15m+65.5)
=0.05m+12.5(元)。
答:该月他们的话费差是(0.05m+12.5)元。
(3)150+(118﹣88)÷0.2
=150+30÷0.2
=50+150
=300(分钟)
答:小文的主叫时间是300分钟。
故答案为:102,118;300。
【点评】此题考查的目的是理解掌握单价、数量、总价三者之间的关系及应用,分段计费的方法及应用。
33.(2024 沙坪坝区)如图,ABCD是长方形,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求三角形DFG(阴影部分)的面积。
【答案】20。
【分析】分析题意,由点G是线段FC的中点可知三角形DFG和三角形DCG的面积相等,则只需求出三角形FDC的面积即可;观察图形可知,三角形FDC的面积=梯形EDCB的面积﹣三角形EDF的面积﹣三角形BFC的面积,连接CE,由三角形和梯形的面积公式易得三角形EDC和梯形EDCB的面积,从而求得三角形BCE的面积;再根据F是BE的中点不难求得三角形EDF的面积,且三角形BFC的面积是三角形BCE面积的一半,由此求得三角形BFC的面积,根据第二步中的关系求出三角形FDC的面积,至此便可求得三角形DFG(阴影部分)的面积。
【解答】解:连接CE。
S△EDC=4×10÷2=20
S梯形EDCB=(4+12)×10÷2=80
所以S△BFC=(80﹣20)÷2=30,S△EDF=4×5÷2=10,
所以S阴影=(80﹣30﹣10)÷2=20。
答:三角形DFG(阴影部分)的面积是20。
【点评】此题解答的关键是明确:等底等高的三角形的面积相等,根据三角形的面积公式、梯形的面积公式解答。
34.(2024 渝北区)有一项工程,由甲、乙、丙三个工程队每天轮流做。原计划按甲、乙、丙次序轮流做,恰好整数天完成。如果按乙、丙、甲次序轮做,比原计划多用0.5天;如果按丙、甲、乙次序做,比原计划多用天。已知甲单独做13天完成。且3个工程队的工效各不相同。这项工程由甲、乙、丙合作要多少天完工?
【答案】天。
【分析】据题意可知,按甲、乙、丙次序轮做,恰好整天完工,其余两个方案都不是整天完工,那么甲乙丙的方案,一定是甲或乙结尾,不可能是丙结束,丙结束就是整数周期.所以按两种情况分析:第一种情况是甲结束,甲=乙+丙丙+甲,丙甲,乙甲,这样丙、乙的工作效率就相同了,据题意,三队的工作效率各不相同,从而排除第一种情况;第二种情况,乙结束,甲+乙=乙+丙+甲丙+甲+乙,丙=甲乙,丙=甲,乙=甲,所以三个工程队合作的时间是13÷(1)(天)。
【解答】解:根据条件可从如下两种情况进等分析:
第一种情况是按甲、乙、丙次序轮做,甲结束:
甲=乙+丙丙+甲,丙甲,乙甲,
这样丙、乙的工作效率就相同了,据题意,三队的工作效率各不相同,从而排除第一种情况;
第二种情况是按甲、乙、丙次序轮做,乙结束:
甲+乙=乙+丙+甲丙+甲+乙,丙=甲乙,丙=甲,乙=甲,
所以三个工程队合作的时间是13÷(1)(天)。
答:那么这项工程由甲、乙、丙三个队合作要天完成。
【点评】完成本题要据所给条件分两种情况以甲为1进行认真的分析,从而得出另两个队的工作效率。
35.(2024 渝北区)如图,A、B是一条道路的两端点,亮亮在A点,明明在B点,两人同时出发,相向而行,他们在离A点100米的C点第一次相遇,亮亮到达B点后返回A点,明明到达A点后返回B点,两人在离B点80米的D点第二次相遇。整个过程中,两人各自的速度都保持不变,求A、B间的距离。
【答案】220米。
【分析】从出发到第一次相遇,两人一共走了1个全程,其中亮亮走了100米;第二次相遇时,两人共走了2个全程,其中亮亮走了2个100米,即两人一共走了3个全程,亮亮一共走了3个100米,又因为亮亮从出发到第二次相遇,一共走了1个全程多80米,所以A、B间的距离为:300﹣80,据此计算即可解答。
【解答】解:第一次相遇,两人一共走了1个全程,其中亮亮走了100米;
第二次相遇时,两人共走了2个全程,因为亮亮走(CB+DB)用的时间是2个走AC的时间,所以走的路程也是2个AC,则亮亮走的路程为:CB+DB=2AC=2×100=200(米),
从出发到第二次相遇亮亮一共走的路程为:100+200=300(米),
又因为亮亮从出发到第二次相遇,一共走了1个全程多80米,即A、B间距离+80=300,所以A、B间的距离为:300﹣80=220(米)。
答:A、B间的距离是220米。
【点评】此题考查多次相遇问题。解答本题的关键是理清亮亮在两次相遇过程中走的路程,根据亮亮走的路程找出等量关系,再列式计算。
36.(2024 渝北区)在长方形ABCD中,AB=30cm,BC=40cm,如图P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值。
【答案】24厘米。
【分析】连接OP,三角形OBC的面积就等于长方形的面积的,又由三角形OPB的面积+三角形POC的面积=三角形OBC的面积,且OB=OCDB,于是求出DB的长度,问题即可迎刃而解。
【解答】解:连接OP,如图所示:
因为长方形的面积=40×30=1200 ( cm2)
△OBC的面积1200=300 ( cm2)
又因为DB2=302+402=2500(cm)
所以DB=50cm
所以OB=OC=DB=25cm
25×PR25×PQ=300
即25×(PR+PQ )=300
所以PR+PQ=24 cm
答:PQ+PR的值24厘米。
【点评】本题主要考查组合图形的面积的计算,关键利用长方形和三角形面积的关系计算。
37.(2024 渝北区)底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积.
【答案】见试题解答内容
【分析】由题意可知:阴影部分的面积=大圆的面积+小半圆的面积×2(小圆的面积)﹣三角形的面积,据此代入数据即可求解.
【解答】解:S阴影=S大圆+S半圆×2﹣S三角形
=3.14×(6÷2)2+3.14×(6÷2÷2)2﹣6×6
=3.14×9+3.14×2.25﹣18
=28.26+7.065﹣18
=17.325(平方厘米)
答:阴影部分的面积是17.325平方厘米
【点评】解答此题的主要依据是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求解.
38.(2024 重庆)李师傅加工一批零件,原计划每小时加工30个,6小时可以完成,实际每小时比原计划多加工20%,实际加工这批零件比原计划提前几小时?
【答案】1小时。
【分析】要求实际加工这批零件比原计划提前几小时,就要求出实际加工这批零件用了几小时,因实际每小时比原来计划多加工20%,要把原计划加工的个数看作单位“1”,也就实际每天加工的是原计划每天加工的(1+20%),又因原计划每小时加工30个,可求出实际每天加工的个数.又因原计划每小时加工30个,6小时可以完成,可求出这批零件一共多少个.再根据除法的意义,可求出实际加工这批零件用了多少小时,原计划加工用的时间减去实际加工用的时间即可解答。
【解答】解:30×6=180(个)
30×(1+20%)
=30×1.2
=36(个)
180÷36=5(小时)
6﹣5=1(小时)
答:实际加工这批零件比原计划提前1小时。
【点评】本题综合考查了学生对单位“1”的掌握以及根据乘、除法的意义解答应用题的能力。
39.(2024 九龙坡区)甲容器中有500克20%盐水,乙容器中有500克水,先将甲中一半的盐水到入乙,充分搅拌;在将乙中一半的盐水到入甲,充分搅拌;最后将甲中盐水的一部分倒入乙,使甲、乙的盐水重量相同.求此时乙中盐水的浓度是多少?.
【答案】见试题解答内容
【分析】先把盐水看成2部分,即盐水=盐+水,根据“溶质质量=溶液质量×浓度”,甲容器里的盐可以算出:500×20%=100(克),水:500﹣100=400(克),然后甲乙一半,甲这时50克盐,200克水,乙这时500+200=700克水,50克盐,其次乙中一半的盐水再倒入甲:这时甲75克盐,550克水,浓度75÷(75+550)=75÷625=12%,盐水总质量75+550=625(克);这时乙25克盐,350克水,浓度现在不算,最后算,总质量375克,使甲、乙的盐水重量相同,甲给乙:(625﹣375)÷2=250÷2=125(克),甲倒给乙的盐水中含盐:125×12%=15(克),水:125﹣15=110(克),此时乙中盐水的浓度:100%=8%.
【解答】解:甲容器里的盐:500×20%=100(克)
水:500﹣100=400(克)
甲一半给乙,甲这时50克盐,200克水,乙这时500+200=700(克)水,50克盐
乙中一半的盐水再倒入甲:这时甲75克盐,550克水
浓度75÷(75+550),
=75÷625
=3/25
=12%
盐水总质量75+550=625(克)
这时乙25克盐,350克水,总质量375克
使甲、乙的盐水重量相同,甲给乙:(625﹣375)÷2=250÷2=125(克)
甲倒给乙的盐水中含盐:125×12%=15(克)
水:125﹣15=110(克)
此时乙中盐水的浓度:
100%,
100%,
=8%
答:此时乙中盐水的浓度是8%.
【点评】解答此题关键明白:溶质质量=溶液质量×浓度;溶液混合均匀,倒出体积的一半,其中溶质、溶剂占一半;浓度的意义:浓度指某物种在总量中所占的分量.
40.(2024 长沙)某游乐场在开门前有400人排队等待,开门后每分钟来的人数是固定的.一个入场口每分钟可以进来10个游客,如果开放4个入场口.20分钟就没有人排队,现在开放6个入口,那么开门后多少分钟后就没有人排队?
【答案】见试题解答内容
【分析】此题里有两个不变的量:一是开门前排队人数是固定数,即400人;二是开门后每分钟来的人数是固定的.按开4个入场口的已知条件,可求出开门后每分钟来的人数.然后设开放6个入场口开门后x分钟后没有人排队,可按以下两种方式求出开门后x分钟总进场人数:一是根据每分钟1个入场口进客人数可得开6个入场口x分钟的进场人数;二是根据开门后x每分钟来的固定人数加开门前排队的400人,根据这个等量关系即可列出方程.
【解答】解:4个入场口20分钟进入的人数是:
10×4×20=800(人),
开门后20分钟来的人数是:800﹣400=400(人),
开门后每分钟来的人数是:400÷20=20(人),
设开6个入场口x分钟后没有人排队,由题意列方程得
10×6×x=400+20x,
40x=400,
x=10,
答:开放6个入场口10分钟后就没有人排队.
【点评】关键点:一是由已知条件求出开门后每分钟来的人数;二是根据一个入场口每分钟进客量和开门后每分钟来的人数两种方式求开门后设定时间内进客总量这个等量关系.
41.(2024 江北区)对于任意一个四位数m,其各位数字互不相等,若它的千位数字与百位数字的和等于十位数字与个位数字的和,则称这个四位数m为“天平数”,记F(m)为m的各个数位上的数字之和。例如:m=1432,∵1+4=3+2,∴1432是“天平数”,F(1432)=1+4+3+2=10;m=6397,∵6+3≠9+7,∴6397不是“天平数”。
(1)求出F(5234)的值;
(2)已知M,N均为“天平数”,其中M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数),N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c<9,0≤d≤9,a,b,c,d是整数)。若F(M) F(N)=264,求出满足条件的M的最大值与最小值的差。
【答案】(1)14;(2)3600。
【分析】(1)根据“天平数”的概念可知,5+2=3+4=7,即5234是“天平数”,F(5234)为5234的各个数位上的数字之和,即求5234的数字和即可;
(2)根据“天平数”的概念与已知条件列出方程,再求出符合条件的x、y、b的值便即可解答。
【解答】解:(1)F(5234)=5+2+3+4=14
答:F(5234)的值是14。
(2)因为M“天平数”,M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数)
所以x+b+3=2+y,F(M)=x+b+3+2+y
所以x+b=y﹣1
因为N是“天平数”,N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c≤9,0≤d≤9,a,b,c,d是整数)
所以2a+b=c+d,F(N)=2a+b+c+d
因为F(M) F(N)=264
所以(x+b+3+2+y)(2a+b+c+d)=264
即(y﹣1+3+2+y)(2a+b+2a+b)=264
所以(4+2y)(4a+2b)=264
即(2+y)(2a+b)=66
因为0≤y≤9
所以2≤2+y≤11
因为1≤a≤4,0≤b≤6
所以2≤2a+b≤14
根据66=1×66=2×33=3×22=6×11
所以(2+y)(2a+b)=66=6×11
当时,y=4,b为奇数且0≤b≤6
故b为1或3或5。
因为x+b+3=2+y=6
所以x+b=3
又因为1≤x≤9
所以x=2,b=1
此时a=5,不满足1≤a≤4。
即时,无解。
当时,y=9,b为偶数且0≤b≤6
故b为0或2或4或6
因为x+b+3=2+y=11
所以x+b=8
又因为1≤x≤9
所以x=8,b=0或x=6,b=2或x=4,b=4或x=2,b=6
此时a=3或a=2或a=1或a=0,
又1≤a≤4,所以a=3或a=2或a=1。
即,此时M=1000x+100b+320+y=1000×8+100×0+320+9=8329,即M的值为8329;
或,此时M=1000x+100b+320+y=1000×6+100×2+320+9=6529,即M的值为6529;
或,此时M=1000x+100b+320+y=1000×4+100×4+320+9=4729,即M的值为4729。
综上所述,M的值为8329或6529或4729。
所以Mmax=8329,Mmin=4729
Mmax﹣Mmin=8329﹣4729=3600
答:M的最大值与最小值的差是3600。
【点评】本题考查了新定义,不定方程的解,关键是正确理解新定义,解题关键是根据题意列出方程。
42.(2024 石柱县)中国建筑中经常能见到如图的设计。如果图中圆的面积是6.28m2,那么整个图形中所有空白部分的面积是多少m2?(π取3.14)
【答案】2.28m2。
【分析】空白部分的面积即为圆面积减去小正方形的面积,据此解答。
【解答】解:设圆半径为r,则r2=6.28÷3.14=2(m2)
圆的直径即为小正方形对角线,所以小正方形面积=(2r)2÷2=2r2=2×2=4(m2)
6.28﹣4=2.282(m2)
答:整个图形中所有空白部分的面积是2.28m2。
【点评】本题考查了不规则图形面积计算。
43.(2024 渝北区)如图,最小正方形的边长为单位1,25个这样的小正方形拼成一个大正方形ABCD,其中,有7个最小正方形被涂上了阴影;用S表示剩下的18个最小正方形的面积和。
(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形的可能性为 ;
(2)在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边 AD 上,距离A点 0.2 个单位长度;
(3)甲、乙两个机器人分别从A、C两点开始,同时出发绕着正方形ABCD的边行走,甲以每秒3个单位的速度顺时针行走,乙以每秒2个单位的速度逆时针行走,请计算得出:他们之间的第18次相遇在何时在何地?
【答案】(1);(2)AD,0.2;(3)出发后70秒的C。
【分析】(1)根据图示可知,涂色小正方形共计7个,如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形,则涂色小正方形的位置只有2种可能,用可以涂色的小正方形个数除以空白小正方形的个数即可求出可能性大小;
(2)根据正方形对角线把正方形面积平分可知,三角形ABC中的S部分面积为8.5,而直线CP恰好平分S,则S的一半即为9,故P点在线段AD上,根据“形面积=(上底+下底)×高÷2”即可求出P点离A点的单位长度;
(3)甲、乙两个机器人第1次相遇时走过了正方形周长的一半,从第2次相遇到第18次相遇,每次相遇,两个机器人合走一个正方形周长,据此求出甲乙机器人相遇18次需要走过的路程和,根据“时间=路程和÷速度和”即可求出第18次相遇的时间,即第18次相遇时间;再根据“路程=时间×速度”求出甲机器人在甲乙机器人相遇18次时走过的路程,用甲机器人走过的路程除以正方形的周长,根据余数即可推算第18次相遇时的具体位置,据此解答。
【解答】解:(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形涂色方式只有如下图2种涂色方法,如下图所示:
即可能性为2÷18。
(2)因为最小正方形的边长为单位1,
所以S=18×1×1=18
S18=9
如下图所示,连接正方形ABCD的对角线AC,则△ABC中S部分为25×1×1﹣4×1×1=8.5<9,故P点应在线段AD上,
即P点在线段AD上把正方形ABCD分成一个三角形CDP和一个直角梯形ABCP,且三角形CDP和直角梯形ABCP的S部分面积均为9,
所以S梯形ABCP=9+4=13
因为S梯形ABCP=13(AP+BC)AB(AP+5)×5
所以AP=13×2÷5﹣5=0.2
即点P离点A的距离为0.2个单位。P点位置如下图所示:
所以在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边AD上,距离A点0.2个单位长度;
(3)甲、乙两个机器人第18次相遇时走过的路程:4×5÷2+4×5×(18﹣1)=350(个单位)
甲、乙两个机器人第18次相遇时间:350÷(3+2)=70(秒)
甲机器人70秒走过的路程:3×70=210(个单位)
正方形周长:4×5=20(个单位)
210÷20=10(圈)……10(个单位)
因为正方形周长为20个单位,甲机器人从A顺时针出发70秒后正好走了10圈10个单位到达C,即甲、乙机器人之间的第18次相遇在出发后70秒的C。
答:甲、乙两个机器人第18次相遇在出发后70秒的C。
故答案为:(1);(2)AD,0.2。
【点评】本题考查了可能性大小问题的应用以及三角形、梯形面积计算的应用以及行程问题的应用,结合图示仔细分析题干不难解答本题。
44.(2024 北碚区)求图中阴影部分的周长和面积(π取3.14)
【答案】18.84厘米;2.28平方厘米。
【分析】如图:
阴影部分的周长等于2个直径是4÷2=2(厘米)的圆的周长加直径是4厘米的圆的周长的一半,据此解答即可。
如图:
通过“割补”的方法,把下面的2个阴影部分分别割补到左面和右面的空白部分,阴影部分的面积等于半径是4÷2=2(厘米)的半圆的面积减去底是4厘米,高是4÷2=2(厘米)的三角形的面积,据此解答即可。
【解答】解:3.14×(4÷2)×2+3.14×4÷2
=12.56+6.28
=18.84(厘米)
3.14×(4÷2)2÷2﹣4×(4÷2)÷2
=6.28﹣4
=2.28(平方厘米)
答:图中阴影部分的周长是18.84厘米,面积是2.28平方厘米。
【点评】本题考查了圆与组合图形周长和面积计算知识,结合题意分析解答即可。
45.(2024 垫江县)1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人,如图。
(1)观察思考,发现规律:每增加1张桌子,可坐人数就增加 2 人。
(2)如果10张餐桌拼在一起,一共可以坐 22 人。
(3)按这样拼下去,m张餐桌可坐 (2m+2) 人。(用含有字母的式子表示)
【答案】(1)2;(2)22;(3)(2m+2)。
【分析】(1)(2)(3)观察可得规律,1张餐桌可坐4人,就是(2×1+2)人,2张餐桌拼在一起可坐(2×2+
2024-2025学年六年级下册数学西师大版
1.(2024 渝中区)有A、B、C三种盐水,按A与B数量之比2:1混合,得到浓度为13%的盐水;按A与B的数量之比为1:2混合,得到浓度为14%的盐水。如果A、B、C数量之比为1:1:3,混合成的盐水浓度为10.2%。问:盐水C的浓度是多少?
2.(2024 渝中区)一段地下管道预计15个工人每天工作4小时,18天可以完成,后来要求加快速度每天增加3人,并且每天工作时间增加1小时,那么,可以提前几天完成?
3.(2024 丰都县)如图是2024年我县某校三至六年级学生人数统计情况。认真读题,完成后面的问题。
(1)图中,单位“1”是 。
A.三至六年级学生总人数
B.五年级学生人数
(2)算一算,该校五年级学生人数占三至六年级学生总人数的 %。
(3)根据上面的统计图,完善下面的统计表。
年级 三年级 四年级 五年级 六年级
人数 84 100
(4)仔细思考,该校学生人数从六年级到三年级,呈现出的发展趋势是 。
A.逐年增长
B.逐年减少
4.(2024 沙坪坝区)某商场今天卖出男、女皮衣各一件,现价都是990元,其中女式皮衣款式漂亮赚了10%,男式皮衣款式陈旧赔了10%,今天卖出这两件皮衣是赚钱还是赔钱?若是赚钱,赚了多少?若是赔钱,赔了多少?
5.(2024 涪陵区)有一种陀螺(如图),上半部分是圆柱,下半部分是圆锥。经过测试,当圆柱的体积与圆锥的体积之比为4:1时,陀螺会转得又稳又快。已知圆锥的底面直径是4厘米,高是1.5厘米。请你算一算,这个陀螺的体积是多少时才能使陀螺转得又稳又快?(π取3.14)
6.(2023 沙坪坝区)李师傅加工一批零件,第一天加工了48个,第二天比第一天多加工25%,第三天比第二天多加工5%,三天共完成这批零件的95%.这批零件共有多少个?
7.(2017 白银)如图所示,AB=12厘米,ED=DA=6厘米,小虫P从A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.
(1)小虫P从A点出发几秒后,三角形APE是等腰直角三角形?
(2)当小虫P到达C时,另一只小虫Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①小虫Q从A点出发几秒后,四边形AQPE是梯形?
②当∠QPD=45度时,四边形AQPE的面积是多少平方厘米?
8.(2024 渝北区)一个水果商从外地运回2000千克苹果,进价是每千克4元,运费及其他支出是1000元.售完这批水果要损耗25%.
(1)如果要不亏本,每千克苹果至少应卖多少元?
(2)如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利多少元?
9.(2024 沙坪坝区)有一些相同的房间需要粉刷一天,4名师傅去粉刷8个房间,结果其中有40平方米的墙面未来得及刷;同样的时间6名徒弟刷9个房间的墙面。每名师傅比徒弟一天多刷20平方米的墙面。
(1)求每个房间需要粉刷的墙面面积。
(2)某老板现有40个这样的房间需要粉刷,若请3名师傅带3名徒弟去,需要几天完成?
(3)已知每名师傅、每名徒弟每天的工资分别是85元、65元,老板要求在3天内完成40个房间的粉刷任务。问:如何在10个人以内雇佣人员最合算?最低费用是多少?(10人不一定全部雇佣)
10.(2024 渝北区)六年级小语种选修班开课了。第一周参加日语班的男生比女生多10人,第二周参加日语班的男生比第一周少,参加日语班的女生比第一周多,第二周参加日语班课的男生和女生一共有59人,问第一周参加日语班学习的男生和女生各有多少人?
11.(2022 凤凰县)市政府要求地铁集团过江隧道工程12个月完工.现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元.由于前期工程路面较宽,可由甲、乙两队共同施工.随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对中山大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
(1)求两套方案中m和n的值;
(2)通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
12.(2024 九龙坡区)(附加题).右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状,请你计算出它的体积.
13.(2024 九龙坡区)实验小学举行庆“六一”男女大合唱,原计划合唱队中女生人数占合唱队总人数的,后来考虑到合唱效果,将增加5名男生,这时女生与男生人数的比是6:5.合唱队原有女生多少名?
14.(2024 石柱县)如图是小伟跳远时留下的脚印。如果你是裁判员,该怎样测量他的成绩?请在图中画出待测量的线段。
15.(2024 渝北区)如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm.由此可得到木棒长为 cm。
(2)由题(1)的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年才出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁?
16.(2024 渝北区)百舸竞渡,激情飞扬。为纪念爱国诗人屈原,某市举行了龙舟赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间关系的图像,请你根据图像回答下列问题:
(1)1.8分钟时,龙舟 队处于领先地位,在这次龙舟比赛中,龙舟 队先到达终点。
(2)求先到达终点的龙舟队在比赛开始多少分钟后开始领先。
17.(2024 北碚区)给定一个十进制下的自然数n,对于n每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数n的“模二数”,记为M2(n)。如M2(975)=111,M2(385)=101,M2(476)=010,对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1。如975、385的“模二数”111、101相加的运算过程如图所示。
根据以上材料,解决下列问题:
(1)M2(9342)的值为 ,M2(59)+M2(9342)的值为 。
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数为“模二相加不变”。
①判断16与45是否“模二相加不变”,并说明理由。
②与45互为“模二相加不变”的两位数共有 个。
18.(2024 垫江县)推导圆柱的体积。
将圆柱如图切分后拼成一个近似的长方体。切拼前后,圆柱的体积没有发生改变,表面积增加了。
(1)切拼后,长方体的底面积等于原圆柱 的面积;长方体的高等于原圆柱的 。
因为:长方体的体积=底面积×高
所以:圆柱的体积= 。
(2)如果圆柱的底面半径为2厘米,高为6厘米,那么拼成的长方体的表面积是多少平方厘米?
19.(2024 垫江县)从“东方红一号”到“天绘六号”发射成功,中国空间技术研究院研制并成功发射了400个航天器,统称为“四百星”。
发射目标 第一个“百星” 第二个“百星” 第三个“百星” 第四个“百星”
完成时间(年) 41 6 3 2
我国完成“四百星”发射目标一共用了 年。观察上面统计表你有什么感受?
20.(2024 綦江区)如果小东买了这个文具盒(如图),小东与小鹏的钱数之比为2:5;如果小鹏买了这个文具盒,则小东与小鹏的钱数之比为8:13,小东原有多少钱?
21.(2024 石柱县)牛奶含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等。下面是100g牛奶中营养成分情况统计图。
(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分, 的含量最低;乳糖的含量占100g牛奶质量的 %。
(2)下面的四幅扇形统计图中,能反映条形统计图结果的是 ,请说说你选择的理由。
22.(2024 石柱县)画一画,填一填。
(1)以直线b为对称轴,画出圆的轴对称图形。
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。
(3)用数对( , )表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。
23.(2024 垫江县)某市规定:每户每月用水不超过20立方米(含20立方米)时,水费按“基本价”收费;超过20立方米时,不超过20立方米(含20立方米)部分仍按“基本价”收费;超过20立方米的部分按“调节价”收费。李老师家今年三、四月份的用水量和水费如下表所示:
月份 用水量(立方米) 水费(元)
3 15 31.5
4 23 52.8
请你算一算该市水费的“基本价格”和“调节价”分别是每立方米多少元?
(1)基本价格:
(2)调节价:
24.(2024 渝中区)甲乙丙三辆车以一定速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙,甲又比乙晚出发20分,出发后1小时40分钟追上丙,问甲出发后用了多少时间追上乙?
25.(2024 渝中区)张、王二人在银行各有一笔存款,老张存款800元,如果老张从存款中取出1/5,老王从存款中取出75%,那么老张的余款比老王的2倍还多120元.张、王二人原来共有存款多少元?
26.(2024 两江新区)小华从A到B,先下坡再上坡共用7小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?
27.(2024 彭水县)甲、乙两辆抱拉机分别耕A、B两块面积相同的土地。甲拖拉机耕了A地的;乙拖拉机耕了B地的,比甲拖拉机多耕3.6公顷。A、B两块地分别有多少公顷?(画图分析,再解答)
28.(2024 丰都县)李阿姨是一个钟点工,她的工资结算方式是每天200元,每4小时算半天,不足半天的按每小时25元结算。加班每小时30元。下面是李阿姨上周的工作情况统计。
时间 工作时长 加班时长
周一 一天 1小时
周二 4小时
周三 一天 1.5小时
周四 一天 1小时
周五 3小时
(1)李阿姨上周共工作了 个整天, 个半天,外加 个小时,另外还加班 小时。
(2)请你算一算李阿姨上周应得工资共为多少元?
29.(2024 渝中区)阅读下列材料,回答下列问题。
材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”。如65362,362﹣65=297=11×27,称65362是“网红数”。
材料二:对任意的自然数P均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),如5278=52×100+10×7+8,规定:G(P)。
(1)求证:任意两个“网红数”之和一定能被11整除;
(2)已知:s=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5),且a,b均为整数,当s+t为“网红数”时,求G(t)的最大值。
30.(2024 璧山区)育英小学六年级三个班给山区学校捐故事书,其中六(1)班捐得最多,捐了40本,六(2)班与六(3)班捐的本数的比为4:5。以下还有三条关于三个班捐书的信息,其中只有一条是正确的:
①六(1)班捐的本数占六年级三个班捐的本数的25%。
②六(1)班捐的本数与另外两个班捐的本数的比是4:9。
③六(1)班捐的本数比六年级捐的本数的多6本。
哪条信息是正确的?请你说明理由。
31.(2024 九龙坡区)如图所示是一个面积约为1040平方厘米的正六边形,空白部分是6个半径为10厘米的小扇形。求阴影部分的面积是多少平方厘米?
32.(2024 渝北区)移动公司推出一款话费套餐活动,资费标准见表:
套餐月费/元 套餐内容 被叫 套餐外资费
主叫限定时间/分钟 主叫超时费(元/分钟)
58 50 免费 0.25
88 150 0.20
118 350 0.15
说明: ①主叫:主动打电话给别人;被叫:接听别人打进来的电话。 ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟。则当月话费为58+0.25×(60﹣50)=60.5元。
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐。
(1)①小文当月的主叫时间为220分钟,则该月她的话费为 元。
②亮亮当月的主叫时间为220分钟,则该月他的话费为 元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),请用含m的代数式表示该月他们的话费差。
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是 分钟。
33.(2024 沙坪坝区)如图,ABCD是长方形,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求三角形DFG(阴影部分)的面积。
34.(2024 渝北区)有一项工程,由甲、乙、丙三个工程队每天轮流做。原计划按甲、乙、丙次序轮流做,恰好整数天完成。如果按乙、丙、甲次序轮做,比原计划多用0.5天;如果按丙、甲、乙次序做,比原计划多用天。已知甲单独做13天完成。且3个工程队的工效各不相同。这项工程由甲、乙、丙合作要多少天完工?
35.(2024 渝北区)如图,A、B是一条道路的两端点,亮亮在A点,明明在B点,两人同时出发,相向而行,他们在离A点100米的C点第一次相遇,亮亮到达B点后返回A点,明明到达A点后返回B点,两人在离B点80米的D点第二次相遇。整个过程中,两人各自的速度都保持不变,求A、B间的距离。
36.(2024 渝北区)在长方形ABCD中,AB=30cm,BC=40cm,如图P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值。
37.(2024 渝北区)底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积.
38.(2024 重庆)李师傅加工一批零件,原计划每小时加工30个,6小时可以完成,实际每小时比原计划多加工20%,实际加工这批零件比原计划提前几小时?
39.(2024 九龙坡区)甲容器中有500克20%盐水,乙容器中有500克水,先将甲中一半的盐水到入乙,充分搅拌;在将乙中一半的盐水到入甲,充分搅拌;最后将甲中盐水的一部分倒入乙,使甲、乙的盐水重量相同.求此时乙中盐水的浓度是多少?.
40.(2024 长沙)某游乐场在开门前有400人排队等待,开门后每分钟来的人数是固定的.一个入场口每分钟可以进来10个游客,如果开放4个入场口.20分钟就没有人排队,现在开放6个入口,那么开门后多少分钟后就没有人排队?
41.(2024 江北区)对于任意一个四位数m,其各位数字互不相等,若它的千位数字与百位数字的和等于十位数字与个位数字的和,则称这个四位数m为“天平数”,记F(m)为m的各个数位上的数字之和。例如:m=1432,∵1+4=3+2,∴1432是“天平数”,F(1432)=1+4+3+2=10;m=6397,∵6+3≠9+7,∴6397不是“天平数”。
(1)求出F(5234)的值;
(2)已知M,N均为“天平数”,其中M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数),N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c<9,0≤d≤9,a,b,c,d是整数)。若F(M) F(N)=264,求出满足条件的M的最大值与最小值的差。
42.(2024 石柱县)中国建筑中经常能见到如图的设计。如果图中圆的面积是6.28m2,那么整个图形中所有空白部分的面积是多少m2?(π取3.14)
43.(2024 渝北区)如图,最小正方形的边长为单位1,25个这样的小正方形拼成一个大正方形ABCD,其中,有7个最小正方形被涂上了阴影;用S表示剩下的18个最小正方形的面积和。
(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形的可能性为 ;
(2)在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边 上,距离A点 个单位长度;
(3)甲、乙两个机器人分别从A、C两点开始,同时出发绕着正方形ABCD的边行走,甲以每秒3个单位的速度顺时针行走,乙以每秒2个单位的速度逆时针行走,请计算得出:他们之间的第18次相遇在何时在何地?
44.(2024 北碚区)求图中阴影部分的周长和面积(π取3.14)
45.(2024 垫江县)1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人,如图。
(1)观察思考,发现规律:每增加1张桌子,可坐人数就增加 人。
(2)如果10张餐桌拼在一起,一共可以坐 人。
(3)按这样拼下去,m张餐桌可坐 人。(用含有字母的式子表示)
46.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
47.(2024 綦江区)六一班要举行“六一”联欢会,班干部决定买15千克水果.据调查,爱吃香蕉的同学人数和爱吃梨的同学人数的比是2:3.请你帮忙算一算,香蕉和梨分别买多少千克?
48.(2024 渝中区)加工一批零件,甲独做20天完成,乙独做每天完成这批零件的。现在两人合作完成这批零件的加工任务,甲中途休息了5天,乙也休息了若干天,这样用了19天才完成任务。求乙休息的天数?
49.(2023 两江新区)甲、乙两地相距294千米,一辆客车和一辆货车先后从两地出发,相向而行.货车先开出0.5小时后客车开出,已知货车每小时行60千米,客车的速度是货车的1.2倍.客车开出几小时后两车相遇?
50.(2024 彭水县)结合下面某乡村小学学生上学路程所用时间占比统计图,解决下列问题。
①这所小学共有学生 人。
②学生上学需要“30~60分钟”的占全班人数的 %。
③学生上学需要“90分钟以上”的有 人。
④如果小学生每分钟可走70米,学生家庭离学校最远的至少有 km。
⑤如果学生早上6:40起床,洗漱吃早餐需30分钟,你认为这所学校上午第一节课上课时间确定为 时整比较合适。
⑥教育部要求小学生睡眠应达10小时以上。你认为怎样安排晚上睡觉和早上起床时间比较合适?对于上学路程较远的同学你想对他在时间安排上做些什么提示?
51.(2024 彭水县)一种圆台形的坐凳是把圆锥上面部分去掉做成的。请计算出下面这个坐凳的体积。
重庆市小升初真题汇编:应用题
2024-2025学年六年级下册数学西师大版
参考答案与试题解析
1.(2024 渝中区)有A、B、C三种盐水,按A与B数量之比2:1混合,得到浓度为13%的盐水;按A与B的数量之比为1:2混合,得到浓度为14%的盐水。如果A、B、C数量之比为1:1:3,混合成的盐水浓度为10.2%。问:盐水C的浓度是多少?
【答案】8%。
【分析】根据“按A与B的数量之比为2:1混合”,“按A与B的数量之比1:2混合”,“按A、B、C的数量之比1:1:3混合”,从这些条件中我们发现,只要使前两次操作得到的13%的盐水与14%的盐水重量相等,就可以使13%的盐水与14%的盐水混合,得到浓度为(13%+14%)÷2=13.5%的盐水;
依据题意,这种盐水里的A和B的数量比为1:1.现在我们要用这样的盐水与盐水C按照2:3混合,得到浓度为10.2%的盐水;
因为13.5%﹣10.2%=3.3%,这样2份的13.5%的盐水就多了6.6%,这6.6%正好补全了C盐水与10.2%的盐水的差距,据此解答即可。
【解答】解:(13%+14%)÷2
=27%÷2
=13.5%
(13.5%﹣10.2%)×2
=3.3%×2
=6.6%
10.2%﹣6.6%÷3
=10.2%﹣2.2%
=8%
答:C盐水的浓度为8%。
【点评】本题考查了比的应用。
2.(2024 渝中区)一段地下管道预计15个工人每天工作4小时,18天可以完成,后来要求加快速度每天增加3人,并且每天工作时间增加1小时,那么,可以提前几天完成?
【答案】6天。
【分析】先根据“15个工人每天工作4小时,18天可以完成”计算出预计完成这项工程的总工时;再除以现在的工作时间和工人人数,即可求出现在需要的天数;用原来的天数减去现在的天数即可。
【解答】解:(4×18×15)÷(4+1)÷(15+3)
=1080÷5÷18
=216÷18
=12(天)
18﹣12=6(天)
答:可以提前6天完成。
【点评】解答本题的关键是依据工作时间,工作效率以及工作总量之间数量关系。
3.(2024 丰都县)如图是2024年我县某校三至六年级学生人数统计情况。认真读题,完成后面的问题。
(1)图中,单位“1”是 A 。
A.三至六年级学生总人数
B.五年级学生人数
(2)算一算,该校五年级学生人数占三至六年级学生总人数的 25 %。
(3)根据上面的统计图,完善下面的统计表。
年级 三年级 四年级 五年级 六年级
人数 84 100
(4)仔细思考,该校学生人数从六年级到三年级,呈现出的发展趋势是 A 。
A.逐年增长
B.逐年减少
【答案】(1)A;
(2)25;
(3)96,120;
(4)A。
【分析】(1)根据题意可知,单位“1”是三至六年级学生总人数。
(2)用“1”减去三、四、六年级的分率,即可求出五年级学生人数占三至六年级学生总人数的分率。
(3)根据百分数乘法的意义,分别求出四年级、六年级的人数即可。
(4)比较统计表中的数据即可解题。
【解答】解:(1)图中,单位“1”是A,即三至六年级学生总人数。
(2)1﹣30%﹣24%﹣21%=25%
答:该校五年级学生人数占三至六年级学生总人数的25%。
(3)84÷21%=400(人)
400×30%=120(人)
400×24%=96(人)
统计表如下:
年级 三年级 四年级 五年级 六年级
人数 84 96 100 120
(4)84<96<100<120
该校学生人数从六年级到三年级,呈现出的发展趋势是A,即逐年增长。
故答案为:A;25;96,120;A。
【点评】本题考查了根据统计表提供的信息解决实际问题的能力。
4.(2024 沙坪坝区)某商场今天卖出男、女皮衣各一件,现价都是990元,其中女式皮衣款式漂亮赚了10%,男式皮衣款式陈旧赔了10%,今天卖出这两件皮衣是赚钱还是赔钱?若是赚钱,赚了多少?若是赔钱,赔了多少?
【答案】见试题解答内容
【分析】要看是赚钱还是赔钱,需要计算后根据数字进行判断;女式皮衣,可赚10%,把原价看作单位“1”,即现价是原价的(1+10%),根据已知一个数的几分之几是多少,求这个数用除法计算得出女式皮衣的原价,然后根据一个数乘分数的意义,计算出赚的钱数;男式皮衣赔了10%,每件售价也是990元,把原价看作单位“1”,现价是原价的(1﹣10%),根据已知一个数的几分之几是多少,求这个数用除法计算得出男式皮衣的原价,然后根据一个数乘分数的意义算出赔本的钱数;然后进行比较,进而得出结论.
【解答】解:男式皮衣赔本:990÷(1﹣10%)×10%,
=1100×10%,
=110(元);
女式皮衣盈利:990÷(1+10%)×10%,
=900×10%,
=90(元);
110>90,赔钱,
110﹣90=20(元);
答:赔钱,赔20元.
【点评】此题做题时,应先判断出单位“1”,然后根据“已知一个数的几分之几是多少,求这个数用除法计算得出两种服装原价;最后根据一个数乘分数的意义,分别求出盈利的钱数和赔本的钱数,进而比较,得出结论.
5.(2024 涪陵区)有一种陀螺(如图),上半部分是圆柱,下半部分是圆锥。经过测试,当圆柱的体积与圆锥的体积之比为4:1时,陀螺会转得又稳又快。已知圆锥的底面直径是4厘米,高是1.5厘米。请你算一算,这个陀螺的体积是多少时才能使陀螺转得又稳又快?(π取3.14)
【答案】见试题解答内容
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出陀螺中圆锥部分的体积,已知圆柱的体积与圆锥的体积之比为4:1,也就是圆锥的体积相当于陀螺体积的,再根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:3.14×(4÷2)2×1.5
3.14×4×1.5
=6.28×5
=31.4(立方厘米)
答:这个陀螺的体积是31.4立方厘米时才能使陀螺转得又稳又快。
【点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
6.(2023 沙坪坝区)李师傅加工一批零件,第一天加工了48个,第二天比第一天多加工25%,第三天比第二天多加工5%,三天共完成这批零件的95%.这批零件共有多少个?
【答案】见试题解答内容
【分析】先把第一天加工的数量看成单位“1”,第二天加工的数量是第一天的1+25%,用乘法求出第二天加工的个数;
再把第二天加工的个数看成单位“1”,第三天加工的数量是第二天的1+5%,用乘法求出第三天加工的数量;
再把这批零件的总数量看成单位“1”,三天加工的数量和是总数量的95%,求总数量用除法.
【解答】解:48×(1+25%),
=48×125%,
=60(个);
60×(1+5%),
=60×105%,
=63(个);
(48+60+63)÷95%,
=171÷95%,
=180(个);
答:这批零件共有180个.
【点评】解答此题的关键是分清这几个单位“1”的区别,求单位“1”的百分之几用乘法;已知单位“1”的百分之几是多少,求单位“1”用除法.
7.(2017 白银)如图所示,AB=12厘米,ED=DA=6厘米,小虫P从A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.
(1)小虫P从A点出发几秒后,三角形APE是等腰直角三角形?
(2)当小虫P到达C时,另一只小虫Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①小虫Q从A点出发几秒后,四边形AQPE是梯形?
②当∠QPD=45度时,四边形AQPE的面积是多少平方厘米?
【答案】见试题解答内容
【分析】(1)由图可知:当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;然后求出A点到B点的距离及A点到CD中点的距离,进而根据:路程÷速度=时间,分别解答即可;
(2)①当DP∥AQ时,AQPE就是梯形,可设小虫Q从A点出发x秒后四边形AQPE是梯形,列式为12﹣x=2x,解答即可.
②当∠QPD=45°时,PF=6cm,PC+AQ=6cm.又因为小虫Q 的速度是小虫P 的2倍,所以小虫Q 行驶路程也是小虫P 的2倍,AQ=64cm,r然后将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积,进一步解答即可.
【解答】解:(1)如图:
当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,
需要:12÷1=12(秒);
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,
需要:(12+6+6)÷1
=24÷1
=24(秒);
答:小虫P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形.
(2)①如图:
可设小虫Q从A点出发x秒后四边形AQPE是梯形,
12﹣x=2x
3x=12
x=4
答:小虫Q从A点出发4秒后,四边形AQPE是梯形.
②如图:
图中小虫Q从A 点向上运动,小虫P 同时从C 点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm.又因为小虫Q 的速度是小虫P 的2倍,所以小虫Q 行驶路程也是小虫P 的2倍,AQ=64cm.而四边形AQPE 为四边形,可以将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积是(4+10)×6÷2=42cm2,6×10÷2=30cm2,所以四边形面积为72 cm2.
【点评】明确当小虫P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;是解答此题的关键.解决本题我们运用了等腰直角三角形的知识、梯形的性质及行程问题的基本数量关系,运用了转化的解题策略,还运用了分情况全面考虑问题的方法.
8.(2024 渝北区)一个水果商从外地运回2000千克苹果,进价是每千克4元,运费及其他支出是1000元.售完这批水果要损耗25%.
(1)如果要不亏本,每千克苹果至少应卖多少元?
(2)如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利多少元?
【答案】见试题解答内容
【分析】(1)先用总重量乘每千克的进价是总进价,然后再加上运费就是成本价;进而把运进苹果的总重量看成单位“1”,售出的苹果重量为苹果总重量的(1﹣25%),由此求出实际售出的苹果重量;然后根据:总价÷数量=单价,即可求出每千克苹果至少应卖的单价;
(2)先求出实际售出的苹果重量,然后乘单价,求出实际卖到的总钱数,然后减去成本价,即可求出盈利的钱数.
【解答】(1)(4×2000+1000)÷[2000×(1﹣25%)]
=9000÷1500
=6(元)
答:如果要不亏本,每千克苹果至少应卖6元.
(2)7×2000×(1﹣25%)﹣(4×2000+1000)
=10500﹣9000
=1500(元)
答:如果每千克苹果卖7元,这个水果商卖完这批苹果可盈利1500元.
【点评】解答此题的关键是:认真分析题意,明确题中数量间的基本关系,然后根据单价、数量和总价三者之间的关系,进行解答.
9.(2024 沙坪坝区)有一些相同的房间需要粉刷一天,4名师傅去粉刷8个房间,结果其中有40平方米的墙面未来得及刷;同样的时间6名徒弟刷9个房间的墙面。每名师傅比徒弟一天多刷20平方米的墙面。
(1)求每个房间需要粉刷的墙面面积。
(2)某老板现有40个这样的房间需要粉刷,若请3名师傅带3名徒弟去,需要几天完成?
(3)已知每名师傅、每名徒弟每天的工资分别是85元、65元,老板要求在3天内完成40个房间的粉刷任务。问:如何在10个人以内雇佣人员最合算?最低费用是多少?(10人不一定全部雇佣)
【答案】(1)60平方米;(2)4天;(3)1755元。
【分析】(1)根据题意可得等量关系:每名师傅每天粉刷的面积﹣每名徒弟每天粉刷的面积=每名师傅比徒弟一天多刷的面积,其中每名师傅每天粉刷的面积,每名徒弟每天粉刷墙面的面积,据此列出方程,并求解。
(2)由上一题分别求出每名师傅、每名徒弟每天粉刷的面积,然后用总面积除以3名师傅和3名徒弟每天粉刷的面积和,即可求出所需的天数。
(3)先求出3天完成粉刷40个这样的房间,每天需粉刷的面积,再根据师傅和徒弟每天粉刷的面积,考虑几种雇佣人员的情况,分别计算出每种情况的花费,比较后得出结论,并计算出最低花费。
【解答】解:(1)设每个房间需要粉刷的墙面面积是x平方米。
20
1212=20×12
3(8x﹣40)﹣18x=240
24x﹣120﹣18x=240
6x﹣120=240
6x﹣120+120=240+120
6x=360
6x÷6=360÷6
x=60
答:每个房间需要粉刷的墙面面积是60平方米。
(2)每名师傅每天粉刷墙面的面积为:
=110(平方米)
每名徒弟每天粉刷墙面的面积为:110﹣20=90(平方米)
40个这样的房间粉刷墙面需用时:
(40×60)÷(110×3+90×3)
=2400÷(330+270)
=2400÷600
=4(天)
答:需要4天完成。
(3)40个这样的房间3天完成粉刷,每天需粉刷的面积:
40×60÷3
=2400÷3
=800(平方米)
情况一:全部雇佣徒弟粉刷,需要人数:
800÷90=8(名)……80(平方米)
徒弟需:8+1=9(人)
一天的费用:65×9=585(元)
情况二:雇佣4名师傅,还需徒弟:
(800﹣110×4)÷90
=(800﹣440)÷90
=360÷90
=4(名)
一天的费用:
85×4+65×4
=340+260
=600(元)
情况三:全部雇佣师傅粉刷,需要人数:
800÷110=7(名)……30(平方米)
师傅需:7+1=8(人)
一天的费用:85×8=680(元)
585<600<680
雇佣9名徒弟粉刷3天的费用:
585×3=1755(元)
答:雇佣9名徒弟粉刷最合算,最低费用是1755元。
【点评】(1)考查列方程解决问题,从题目中找出等量关系,按等量关系列出方程。
(2)求出每名师傅和每名徒弟的工作效率是解题本题的关键。
(3)先求出每天规定的工作量,再安排方案,根据每天的花费找出最佳方案。
10.(2024 渝北区)六年级小语种选修班开课了。第一周参加日语班的男生比女生多10人,第二周参加日语班的男生比第一周少,参加日语班的女生比第一周多,第二周参加日语班课的男生和女生一共有59人,问第一周参加日语班学习的男生和女生各有多少人?
【答案】40人,30人。
【分析】设第一周参加日语班的女生有x人,则男生有(10+x)人;第二周参加日语班的男生有(10+x)×(1),第二周参加日语班的女生有(1)x人,合起来其共59人。根据这个等量关系列方程解答。
【解答】解:设第一周参加日语班的女生有x人,则男生有(10+x)人。
(10+x)×(1)+(1)x=59
6xx=59
6x﹣6=59﹣6
x53
x=30
当x=30时,10+x=10+30=40
答:第一周参加日语班学习的男生有40人,女生有30人。
【点评】列方程解决问题的关键是准确分析题目中的等量关系。
11.(2022 凤凰县)市政府要求地铁集团过江隧道工程12个月完工.现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元.由于前期工程路面较宽,可由甲、乙两队共同施工.随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对中山大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
(1)求两套方案中m和n的值;
(2)通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
【答案】见试题解答内容
【分析】(1)由于甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成,所以甲做了12个月,乙做了m个月,则甲完成了全部的12,乙完成了全部的m,由此可得:12m=1.由于由②可得:.进而解方程求出m=6,n=8.
(2)方案①需要资金12×600+6×400=9600万元,方案②需要资金400×12+600×8=9600万元,即两种方案所需资金相同,由于方案①合作时间较短,对交通影响较小,所以应选择方案①.
【解答】解:(1)
m=1
m
m=6
n=1
n
n=8.
答:方案①中两队合作6天,方案②中两队合作8天.
(2)方案①需要资金12×600+6×400=9600万元,
方案②需要资金400×12+600×8=9600万元,
即两种方案所需资金相同.
由于方案①合作时间较短,对交通影响较小,所以应选择方案①.
【点评】完成本题要注意分析所给条件,然后根据工作效率、工作时间及工作量之间的关系列出方程解答.
12.(2024 九龙坡区)(附加题).右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状,请你计算出它的体积.
【答案】见试题解答内容
【分析】可以把这个组合形体看成两部分,上面是圆柱的一半,下面是圆柱,它们的体积之和即是这个物体的体积.
【解答】解;7﹣5=2( 厘米),
3.14×32×2÷2=28.26(立方厘米),
3.14×32×5=141.3(立方厘米),
28.26+141.3=169.56(立方厘米),
答:它的体积是169.56立方厘米.
【点评】此题主要考查圆柱的体积公式及其计算.
13.(2024 九龙坡区)实验小学举行庆“六一”男女大合唱,原计划合唱队中女生人数占合唱队总人数的,后来考虑到合唱效果,将增加5名男生,这时女生与男生人数的比是6:5.合唱队原有女生多少名?
【答案】见试题解答内容
【分析】原计划合唱队中女生人数占合唱队总人数的,则男生是女生的(1),男生增加5名后,男生是女生的,则这5名男生占女生人数的,根据分数除法的意义,用5人除以()就是原有女生人数.
【解答】解:原来男生是女生的:
(1)
则合唱队原有女生:
5÷()
=5
=30(人)
答:合唱队原有女生30人.
【点评】明确这一过程中,女生人数没有发生变化,从而根据男生占女生人数分率的变化求出女生有多少人是完成本题的关键.
14.(2024 石柱县)如图是小伟跳远时留下的脚印。如果你是裁判员,该怎样测量他的成绩?请在图中画出待测量的线段。
【答案】
【分析】此题为数学知识的应用,由实际出发,老师测量跳远成绩的依据是垂线段最短,即测量后脚印与起跳线间的垂直距离即为跳远成绩。
【解答】解:如图:
【点评】此题考查知识点垂线段最短。
15.(2024 渝北区)如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm.由此可得到木棒长为 5 cm。
(2)由题(1)的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年才出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁?
【答案】见试题解答内容
【分析】(1)根据题意并结合题图,我们可轻松得到:从刻度5到刻度20之间的线段长度正好是这根木棒长度的3倍.据此即可求出答案.
(2)此题中爷孙俩的年龄差就相当于上题中的木棒长度,这样即可轻松求出他们的年龄差为:(125+40)÷3=55岁.再结合“你若是我现在这么大,我已经125岁”便可求出爷爷现在的年龄.
【解答】解:(1)20﹣5=15(cm)
15÷3=5(cm)
答:木棒长为5cm.
(2)125+40=165(岁)
165÷3=55(岁)
125﹣55=70(岁)
答:爷爷现在70岁.
【点评】解答此题的关键是,理解木棒长度与两个刻度之间长度的关系即可轻松作答.
16.(2024 渝北区)百舸竞渡,激情飞扬。为纪念爱国诗人屈原,某市举行了龙舟赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间关系的图像,请你根据图像回答下列问题:
(1)1.8分钟时,龙舟 甲 队处于领先地位,在这次龙舟比赛中,龙舟 乙 队先到达终点。
(2)求先到达终点的龙舟队在比赛开始多少分钟后开始领先。
【答案】(1)甲,乙;(2)3.4分。
【分析】(1)根据图示可知,甲、乙两支龙舟队出发后,甲队在2.2分钟前一直处于领先位置,但最后乙队用时3.8分到达目的地,甲队用时4分钟到达目的地,即乙队先到达终点;
(2)根据图示可知,甲队从出发到到达终点处于匀速运动,速度一直没有变化,根据“速度=路程÷时间”求出甲龙舟队的划行速度;根据“路程=速度×时间”求出甲队在2.2分时划行的路程,根据图示可知,2.2分时乙队划行了400米,两者作差即可求出2.2分时甲队和乙队的路程差;根据图示可知,从2.2分开始,乙队开始加速,根据图示可知,乙队从2.2分到到达终点的3.8分共用时(3.8﹣2.2)时间内共划行了(1000﹣400)米,根据“速度=路程÷时间”求出乙队从2.2分开始时的速度;根据“追及时间=路程差÷速度差”求出乙队追上甲队的用时,用乙队开始加速时的时间2.2分加上追及时间即是乙队领先的时间,据此解答。
【解答】解:(1)1.8分钟时,龙舟甲队处于领先地位,在这次龙舟比赛中,龙舟乙队先到达终点。
(2)甲队的速度:1000÷4=250(米/分)
2.2分时甲队划行路程:2.2×250=550(米)
2.2分时甲、乙队划行路程差:550﹣400=150(米)
2.2分到3.8分乙队的速度:(1000﹣400)÷(3.8﹣2.2)=375(米/分)
乙队追上甲队的用时:150÷(375﹣250)=1.2(分)
乙队追上甲队的时间:2.2+1.2=3.4(分)
答:先到达终点的龙舟队在比赛开始3.4分钟后开始领先。
【点评】本题考查了行程问题的应用以及学生能读懂统计图并根据统计图解决问题的能力。
17.(2024 北碚区)给定一个十进制下的自然数n,对于n每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数n的“模二数”,记为M2(n)。如M2(975)=111,M2(385)=101,M2(476)=010,对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1。如975、385的“模二数”111、101相加的运算过程如图所示。
根据以上材料,解决下列问题:
(1)M2(9342)的值为 1100 ,M2(59)+M2(9342)的值为 1111 。
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数为“模二相加不变”。
①判断16与45是否“模二相加不变”,并说明理由。
②与45互为“模二相加不变”的两位数共有 30 个。
【答案】(1)1100,1111;(2)①否,因为16和45的和的“模二数”与它们的“模二数”的和不相等;②30。
【分析】(1)根据“模二数”的定义,直接计算M2(9342),M2(59)即可;然后再根据“模二数”的加法规定计算M2(59)+M2(9342)即可;
(2)①根据两个数为“模二相加不变”的定义,计算M2(16+45)与M2(16)+M2(45)是否相等即可判断;
②根据模二结果数分别为10、11、01、00分别讨论即可找出和45互为“模二相加不变”的两位数。
【解答】解:(1)M2(9342)的值为1100
M2(59)+M2(9342)
=11+1100
=1111
即M2(59)+M2(9342)的值为1111。
(2)①M2(16+45)=M2(61)=01
M2(16)+M2(45)=10+01=11
即16和45的和的“模二数”与它们的“模二数”的和不相等,即这两个数不是“模二相加不变”。
②M2(45)=01
模二结果是10的两位数有:12,32,52,72,92,14,34,54,74,94,16,36,56,76,96,18,38,58,78,98,10,30,50,70,90,共计25个;
10+01=11
即满足题意的模二结果是10的两位数有:12,32,52,14,34,54,10,30,50,共计9个两位数满足题意。
模二结果是11的两位数有:11,31,51,71,91,13,33,53,73,93,15,35,55,75,95,17,37,57,77,97,19,39,59,79,99,共计25个;
11+01=100
即满足题意的模二结果是11的两位数有:55,75,95,57,77,97,59,79,99,共计9个两位数满足题意。
模二结果是01的两位数有:21,23,25,27,29,41,43,45,47,49,61,63,65,67,69,81,83,85,87,89,共计20个;
01+01=10
即满足题意的模二结果是01的两位数有:25,27,29,45,47,49,共计6个两位数满足题意。
模二结果是00的两位数有:20,22,24,26,28,40,42,44,46,48,60,62,64,66,68,80,82,84,86,88,共计20个;
00+01=01
即满足题意的模二结果是00的两位数有:20,22,24,40,42,44,共计6个两位数满足题意。
所以与45互为“模二相加不变”的两位数共有:9+9+6+6=30(个)
答:与45互为“模二相加不变”的两位数共有30个。
故答案为:(1)1100,1111;(2)②30。
【点评】本题考查了定义新运算的应用,数字的变化规律的应用,理解定义内容,能将定义与已学内容相结合是解题的关键。
18.(2024 垫江县)推导圆柱的体积。
将圆柱如图切分后拼成一个近似的长方体。切拼前后,圆柱的体积没有发生改变,表面积增加了。
(1)切拼后,长方体的底面积等于原圆柱 底面 的面积;长方体的高等于原圆柱的 高 。
因为:长方体的体积=底面积×高
所以:圆柱的体积= 底面积×高 。
(2)如果圆柱的底面半径为2厘米,高为6厘米,那么拼成的长方体的表面积是多少平方厘米?
【答案】(1)底面,高,底面积×高;
(2)124.48平方厘米。
【分析】(1)根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后体积不变,表面积增加了,拼成的长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,根据长方体的体积公式推导出圆柱的体积公式。
(2)拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,根据圆柱的表面积=侧面积+底面积×2,长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)切拼后,拼成的长方体的底面积等于原圆柱的底面积,长方体的高等于原圆柱的高。
因为长方体的体积=底面积×高,
所以圆柱的体积=底面积×高。
(2)2×3.14×2×6+3.14×22×2+6×2×2
=12.56×6+3.14×4×2+12×2
=75.36+25.12+24
=124.48(平方厘米)
答:拼成的长方体的表面积是124.48平方厘米。
故答案为:底面,高,底面积×高。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导方法及应用,圆柱的表面积公式、长方体的表面积公式及应用。
19.(2024 垫江县)从“东方红一号”到“天绘六号”发射成功,中国空间技术研究院研制并成功发射了400个航天器,统称为“四百星”。
发射目标 第一个“百星” 第二个“百星” 第三个“百星” 第四个“百星”
完成时间(年) 41 6 3 2
我国完成“四百星”发射目标一共用了 52 年。观察上面统计表你有什么感受?
【答案】52;中国空间技术研究院研制“四百星”时间用的越来越少。(答案不唯一)
【分析】把4个数字相加,就是我国完成“四百星”发射目标一共用了多少年;感受:根据完成时间的长短解答即可。
【解答】解:41+6+3+2
=47+3+2
=50+2
=52(年)
答:我国完成“四百星”发射目标一共用了52年。
41>6>3>2
发现:中国空间技术研究院研制“四百星”时间用的越来越少。(答案不唯一)
故答案为:52。
【点评】熟练掌握整数加减法和比较大小的方法是解答本题的关键。
20.(2024 綦江区)如果小东买了这个文具盒(如图),小东与小鹏的钱数之比为2:5;如果小鹏买了这个文具盒,则小东与小鹏的钱数之比为8:13,小东原有多少钱?
【答案】20元。
【分析】由题意可知:小东和小鹏剩余的钱数的是不变的,把二人剩余的钱数看作单位“1”,则小东买了这个文具盒后,他剩余的钱数占总剩余钱数的,当小鹏买了这个文具盒后,小东的钱数,占总剩余钱数的,增加了(),增加的分率所对应的量是5元,于是用对应量5除以对应分率(),就得到二人剩余钱数的总量,进而根据求一个数的几分之几是多少,用乘法即可求解。
【解答】解:5÷()
=5÷()
=5
=52.5
=20(元)
答:小东原来有20元钱。
【点评】解答此题的关键是:先求出5元所对应的剩余钱数总量的几分之几,从而可以求出剩余的总钱数,进而求出小东原来的钱数。
21.(2024 石柱县)牛奶含有丰富的营养成分,其中主要成分有水、蛋白质、脂肪、乳糖等。下面是100g牛奶中营养成分情况统计图。
(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分, 其它营养成分 的含量最低;乳糖的含量占100g牛奶质量的 4.9 %。
(2)下面的四幅扇形统计图中,能反映条形统计图结果的是 B ,请说说你选择的理由。
【答案】(1)其它营养成分,4.9,(2)B,我的理由是蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意,B图符合题意。
【分析】(1)观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分,其它营养成分的含量最低。用乳糖的含量除以100克就得乳糖的占比。
(2)蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意。
【解答】解:(1)4.9÷100=4.9%
答:观察统计图,100g牛奶中的蛋白质、脂肪、乳糖三种营养成分,其它营养成分的含量最低;乳糖的含量占100g牛奶质量的4.9%。
(2)四幅扇形统计图中,能反映条形统计图结果的是B。我的理由是蛋白质、脂肪、乳糖、其它营养成分的总和占牛奶总量的13%,A和D图这4中成分占牛奶总量超过25%,不符合题意,C图表示4种成分占的百分比超过13%,且四种成分占比差别不大,不符合题意,B图符合题意。
故答案为:其它营养成分,4.9,B。
【点评】本题考查了学生对数据的掌握及从统计图中获取信息的能力。
22.(2024 石柱县)画一画,填一填。
(1)以直线b为对称轴,画出圆的轴对称图形。
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。
(3)用数对( 2 , 3 )表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。
【答案】(1)(2)(3),2,3。
【分析】(1)根据轴对称图形的画法,以直线b为对称轴,在对称轴的右面画出圆的轴对称图形即可。
(2)根据图形旋转的方法,点P拨动,画出三角形先绕点P逆时针旋转90°后的图形,形状不变,并标注“①”,再根据图形平移的方法,画出图形①向上平移4格后的图形即可。
(3)用数对(2,3)表示点M的位置;根据图形缩小的方法,按1:3的比画出长方形缩小到原来后的图形,并标注“②”即可。
【解答】解:(1)以直线b为对称轴,画出圆的轴对称图形。如图:
(2)画出三角形先绕点P逆时针旋转90°后的图形,并标注“①”,再画出图形①向上平移4格后的图形。如图:
(3)用数对(2,3)表示点M的位置;按1:3的比画出长方形缩小后的图形,并标注“②”。如图:
故答案为:2,3。
【点评】本题考查了轴对称图形、图形的旋转、平移、图形的缩小以及数对表示位置知识,结合题意分析解答即可。
23.(2024 垫江县)某市规定:每户每月用水不超过20立方米(含20立方米)时,水费按“基本价”收费;超过20立方米时,不超过20立方米(含20立方米)部分仍按“基本价”收费;超过20立方米的部分按“调节价”收费。李老师家今年三、四月份的用水量和水费如下表所示:
月份 用水量(立方米) 水费(元)
3 15 31.5
4 23 52.8
请你算一算该市水费的“基本价格”和“调节价”分别是每立方米多少元?
(1)基本价格:
(2)调节价:
【答案】(1)2.1元;(2)3.6元。
【分析】(1)3月份的用水量为15立方米,不超过20立方米(含20立方米),水费除以用水量可得”基本价格“,据此作答即可。
(2)4月份的用水量为23立方米,超过20立方米(含20立方米),水费总额先减去20立方米乘“基本价格”的结果,余额除以超过20立方米的用水量,可得”调节价“,据此作答即可。
【解答】解:(1)31.5÷15=2.1(元)
答:该市水费的“基本价格”是每立方米2.1元。
(2)(52.8﹣2.1×20)÷(23﹣20)
=(52.8﹣42)÷3
=10.8÷3
=3.6(元)
答:该市水费的“调节价”是每立方米3.6元。
【点评】本题考查了整数、小数混合运算的应用问题。
24.(2024 渝中区)甲乙丙三辆车以一定速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙,甲又比乙晚出发20分,出发后1小时40分钟追上丙,问甲出发后用了多少时间追上乙?
【答案】见试题解答内容
【分析】根据已知条件得知,乙用40分钟所走的距离与丙用50分钟所走的距离相等,所以丙的速度是乙的;甲用100分钟所走的距离与丙用130分钟所走的距离相等.故丙用130分钟所走的距离,乙用了:130104(分钟),即甲用100分钟走的距离,乙用104分钟走完.由于甲比乙晚出发20分钟,当甲追上乙时,设甲用了x分钟,则乙用了(x+20)分钟,由此可得方程:.
【解答】解:丙用130分钟所走的距离,乙用了:
130104(分钟),
设甲用了x分钟,可得:
,
104x=100(x+20),
104x=100x+2000,
4x=2000,
x=500.
答:甲出发后需要500分钟才能追上乙.
【点评】首先根据行驶相同的距离、所用时间与速度成反比求出他们的速度比是完成本题的关键.
25.(2024 渝中区)张、王二人在银行各有一笔存款,老张存款800元,如果老张从存款中取出1/5,老王从存款中取出75%,那么老张的余款比老王的2倍还多120元.张、王二人原来共有存款多少元?
【答案】见试题解答内容
【分析】先把老张原来的存款钱数看成单位“1”,余下的钱数是总钱数的(1),由此用乘法求出剩下的钱数;再根据老张的余款比老王的2倍还多120元,求出老王剩下的钱数;然后把乙原来的存款钱数看成单位“1”,剩下的钱数是它的(1﹣75%),由此用除法求出老王原来的存款钱数,据此再把他们的钱数加起来即可.
【解答】解:老张剩下的钱数是:800×(1)=640(元),
则老王剩下的钱数是:(640﹣120)÷2,
=520÷2,
=260(元),
所以老王的存款是:260÷(1﹣75%),
=260÷25%,
=1040(元),
1040+800=1840(元),
答:二人原来共有1840元存款.
【点评】解答此题的关键是分清两个单位“1”的区别,再根据二人的余款关系进行求解.
26.(2024 两江新区)小华从A到B,先下坡再上坡共用7小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?
【答案】见试题解答内容
【分析】方法1:①要求原路返回所用的时间,需要求出,上坡路的距离和下坡路的距离分别是多少;所以这里可以根据题干先求出去时的上坡路程和下坡路程;
②根据题干,设小华从A到B上坡路程为x千米,则下坡路程为(24﹣x)千米,根据速度、时间和路程的关系,利用上坡路用的时间+下坡路用的时间=总时间,即可列出方程求得去时的上坡路程和下坡路程,从而得出返回时的上坡路程和下坡路程,即可解决问题;
方法2:去时上坡就是回来时的下坡,去时下坡就是回来时上坡,由此可知全程上坡24千米,下坡24千米,所以全程用时24÷4+24÷3=14(小时),减去去时用时即可求解.
【解答】解:方法1:设小华从A到B上坡路程为x千米,则下坡路程为24﹣x千米,根据题意可得方程:
7
4x+72﹣3x=2×43
x=14,
24﹣14=10(千米),
那么可得返回时上坡路为10千米,下坡路为14千米:
,
(小时),
方法2:24÷4+24÷3
=6+8
=14(小时),
14﹣7(小时).
答:返回时用的时间是小时.
【点评】此题考查了速度、时间和路程之间的关系的灵活应用,这里抓住来回时,上坡和下坡的路程正好相反,是解决本题的关键.
27.(2024 彭水县)甲、乙两辆抱拉机分别耕A、B两块面积相同的土地。甲拖拉机耕了A地的;乙拖拉机耕了B地的,比甲拖拉机多耕3.6公顷。A、B两块地分别有多少公顷?(画图分析,再解答)
【答案】;21公顷。
【分析】根据题意可知A、B两块面积相同,把A地面积看作单位“1”,平均分成5份,其中的2份就是甲拖拉机耕的面积;把B地面积看作单位“1”,平均分成7份,其中的4份就是乙拖拉机耕的面积;乙拖拉机比甲拖拉机多耕3.6公顷;据此画出线段图;乙拖拉机比甲拖拉机多耕了单位“1”的(),对应的数量是3.6公顷,然后再用3.6除以()即可。
【解答】解:画图如下:
3.6÷()
=3.6
=21(公顷)
答:A、B两块地分别有21公顷。
【点评】本题关键是根据题意画出线段图,弄清数量关系,然后再列式解答。
28.(2024 丰都县)李阿姨是一个钟点工,她的工资结算方式是每天200元,每4小时算半天,不足半天的按每小时25元结算。加班每小时30元。下面是李阿姨上周的工作情况统计。
时间 工作时长 加班时长
周一 一天 1小时
周二 4小时
周三 一天 1.5小时
周四 一天 1小时
周五 3小时
(1)李阿姨上周共工作了 3 个整天, 1 个半天,外加 3 个小时,另外还加班 3.5 小时。
(2)请你算一算李阿姨上周应得工资共为多少元?
【答案】(1)3,1,3,3.5;
(2)880元。
【分析】(1)根据统计表中的数据,按照李阿姨的工资结算方式,数出时间完成填空;
(2)根据单价×数量=总价,分别计算每天、半天、加班的工资,再求和即可。
【解答】解:(1)李阿姨上周共工作了3个整天,1个半天,外加3个小时,另外还加班3.5小时。
(2)3×200+25×(4+3)+30×3.5
=600+175+105
=880(元)
答:李阿姨上周应得工资共为880元。
故答案为:3,1,3,3.5。
【点评】本题考查了根据统计表提供的信息解决实际问题的能力。
29.(2024 渝中区)阅读下列材料,回答下列问题。
材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”。如65362,362﹣65=297=11×27,称65362是“网红数”。
材料二:对任意的自然数P均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),如5278=52×100+10×7+8,规定:G(P)。
(1)求证:任意两个“网红数”之和一定能被11整除;
(2)已知:s=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5),且a,b均为整数,当s+t为“网红数”时,求G(t)的最大值。
【答案】(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数),
根据“网红数”的特征可知:n﹣m=1lk,b﹣a=1lh(或m﹣n=11k,a﹣b=11h),
所以n=11k+m,b=11h+a
所以
=1000m+n+1000a+b
=1000m+11k+m+1000a+11h+a
=1001m+1001a+11(k+h)
=11(91m+9la+k+h)
因为m、a、k、h都是整数,
所以91m+91n+h+k为整数,
所以任意两个“网红数”之和一定能被11整除。
(2)。
【分析】(1)根据题意,设出两个“网红数”,根据“网红数”的特征:末三位表示的数与末三位之前的数字表示的数之差是11的倍数,即把这两个“网红数”分别用后三位和后三位前面的数作差后表示为11的倍数,然后再用位值原理把两个“网红数”表示出来后写成11的倍数的形式即可证明;
(2)根据题意,s+t=300+10b+a+1000b+100a+1142=1010b+101a+1442,根据1≤a≤5或6≤a≤7,因为s+t为“网红数”,则s+t可以表示为末三位表示的数与末三位之前的数字表示的数之差是11的倍数,即该差能被11整除,利用能被11整除的特征分析解答即可求出不同的t值,再把t表示为100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x,y,z均为整数),根据G(t)。分别求出G(t)的值,然后比较大小,找出最大的即可解答本题。
【解答】解:(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数),
根据“网红数”的特征可知:n﹣m=1lk,b﹣a=1lh(或m﹣n=11k,a﹣b=11h),
即n=11k+m,b=11h+a
又
=1000m+n+1000a+b
=1000m+11k+m+1000a+11h+a
=1001m+1001a+11(k+h)
=11(91m+9la+k+h)
因为m、a、k、h都是整数,
所以91m+91n+h+k为整数,
所以11(91m+9la+k+h)是11的倍数,
即一定能被11整除。
所以任意两个“网红数”之和一定能被11整除。
(2)①当1≤a≤5时,
因为s=300+10b+a,t=1000b+100a+1142
所以s+t=(300+10b+a)+(1000b+100a+1142)
=1010b+101a+1442
=1000b+10b+100a+a+1000+400+40+2
=(1000b+1000)+(100a+400)+(10b+40)+(a+2)=1000(b+1)+100(a+4)+10(b+4)+(a+2)
因为s+t为“网红数”,
根据“网红数”的特征可知:(b+1)能被11整除,
即100(a+4)+10(b+4)+(a+2)﹣(b+1)能被11整除,
所以101a+9b+441=11×9a+2a+11b﹣2b+11×40+1=11×(9a﹣2b+40)+(2a﹣2b+1)能被11整除,
因为11×(9a﹣2b+40)能被11整除,
所以只需2a﹣2b+1能被11整除即可,
因为l≤a≤5,0≤b≤5,
所以﹣7≤2a﹣2b+1≤11,
所以2a﹣2b+1=0或11,
此时a=5,b=0,
此时t=1000(b+1)+100(a+1)+4×10+2=1000×(0+1)+100×(5+1)+4×10+2=1642=100×16+10×4+2,
所以G(t)=G(1642)17.07,
②当6≤a≤7时,
因为s=300+10b+a,t=1000b+100a+1142
所以s+t=(300+10b+a)+(1000b+100a+1142)
=1010b+101a+1442
=1000b+10b+100a+a+2000﹣600+40+2
=(1000b+2000)+(100a﹣600)+(10b+40)+(a+2)=1000(b+2)+100(a﹣6)+10(b+4)+(a+2)
因为s+t为“网红数”,
根据“网红数”的特征可知:(b+2)能被11整除,
即100(a﹣6)+10(b+4)+(a+2)﹣(b+2)能被11整除,
所以101a+9b﹣560=11×9a+2a+11b﹣2b﹣11×51+1=11×(9a﹣2b﹣51)+(2a﹣2b+1)能被11整除,
因为11×(9a﹣2b﹣51)能被11整除,
所以只需2a﹣2b+1能被11整除即可,
因为6≤a≤7,0≤b≤5,
所以3≤2a﹣2b+1≤15,
所以2a﹣2b+1=11,
此时a=6,b=1或a=7,b=2,
当a=6,b=1,t=1000(b+1)+100(a+1)+4×10+2=1000×(1+1)+100×(6+1)+4×10+2=2742=100×27+10×4+2,
G(t)=G(2742)28.04,
当a=7,b=2,t=1000(b+1)+100(a+1)+4×10+2=1000×(2+1)+100×(7+1)+4×10+2=3842=100×38+10×4+2,
G(t)=G(3842)39.03,
因为17.07<28.04<39.03,所以G(t)max。
答:G(t)的最大值是。
【点评】本题考查了能被11整除的数的应用以及定义新运算是最值问题的应用,理解题意,从题目中获取信息,列出正确的代数式,再由数的特点求解是解题的关键。
30.(2024 璧山区)育英小学六年级三个班给山区学校捐故事书,其中六(1)班捐得最多,捐了40本,六(2)班与六(3)班捐的本数的比为4:5。以下还有三条关于三个班捐书的信息,其中只有一条是正确的:
①六(1)班捐的本数占六年级三个班捐的本数的25%。
②六(1)班捐的本数与另外两个班捐的本数的比是4:9。
③六(1)班捐的本数比六年级捐的本数的多6本。
哪条信息是正确的?请你说明理由。
【答案】③;六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【分析】①六(1)班捐的本数已知,六(2)、六(3)班捐的本数比已知,如果再告诉六(1)班捐的本数所占的分率或六年级三个个班捐的总本数,才能求出六(1)班捐的本数占六年级三个班捐的本数百分之几。
②同理,无法求出六(1)班捐的本数与另外两个班捐的本数的比。
③六(1)班捐的本数比六年级捐的本数的多6本,六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【解答】解:“六(1)班捐的本数比六年级捐的本数的多6本”是正确的。
理由:六(1)班捐的本数是40本,用40本减6本,正好是六年级捐的本数的。把六年级捐的本数看作单位“1”,根据分数除法的意义,用(40﹣6)本除以就是六年级捐的本数。
【点评】六(1)班与六(2)班、六(3)班捐的本数没有任何联系,无法求出六(1)班捐的本数占六年级三个班总本数的百分之几或六(1)本捐的本数与另外两个班捐的本数之比。
31.(2024 九龙坡区)如图所示是一个面积约为1040平方厘米的正六边形,空白部分是6个半径为10厘米的小扇形。求阴影部分的面积是多少平方厘米?
【答案】412平方厘米。
【分析】由图意可知:所要求的阴影面积=正六边形的面积﹣六个小扇形面积;正六边形的面积已知,现在关键是求小扇形的面积,由扇形面积公式S可知,只需要求出半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么∠AOC=120°,又知四边形ABCD是平行四边形,所以∠ABC=120°,再根据半径为10厘米,求出扇形的面积;从而可以求得阴影部分的面积。
【解答】解:因为正六边形每边所对圆心角为60°,那么∠AOC=120°;
又知四边形ABCO是平行四边形,所以∠ABC=120°。
阴影部分的面积:10403.14×102×6
=10403.14×100×6
=1040﹣628
=412(平方厘米)
答:阴影部分的面积是412平方厘米。
【点评】解答此题的关键是明白:阴影面积是用正六边形的面积减去六个小扇形面积。
32.(2024 渝北区)移动公司推出一款话费套餐活动,资费标准见表:
套餐月费/元 套餐内容 被叫 套餐外资费
主叫限定时间/分钟 主叫超时费(元/分钟)
58 50 免费 0.25
88 150 0.20
118 350 0.15
说明: ①主叫:主动打电话给别人;被叫:接听别人打进来的电话。 ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟。则当月话费为58+0.25×(60﹣50)=60.5元。
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐。
(1)①小文当月的主叫时间为220分钟,则该月她的话费为 102 元。
②亮亮当月的主叫时间为220分钟,则该月他的话费为 118 元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),请用含m的代数式表示该月他们的话费差。
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是 300 分钟。
【答案】(1)102,118;
(2)(0.05m+12.5)元;
(3)300。
【分析】(1)①小文办理的是月使用费为88元的套餐,主叫时间为150分钟,小文当月的主叫时间为220分钟,超过150分钟每分钟收费0.2元,根据分段计费的方法解答;
②亮亮办理的是月使用费为118元的套餐,主叫时间为350分钟,亮亮当月的主叫时间为220分钟,没有超过规定的时间,所以亮亮该月话费为118元。
(2)某月小文与亮亮的主叫时间都为m分钟(m>350),因为m>350分钟,所以两人的话费均有套餐费和主叫超时费两部分组成,根据具体数据列式即可。
(3)由题意可知,小文和亮亮11月的话费都是118元,则小文的主叫时间为50+(118﹣58)÷0.25,据此解答即可。
【解答】解:(1)①88+0.2×(220﹣150)
88+0.2×70
=88+14
=102(元)
答:小文该月话费为102元。
②亮亮当月的主叫时间为220分钟,220分钟<350分钟。
答:亮亮该月他的话费为118元。
(2)小文该月话费为:88+0.2×(m﹣50)
=88+0.2m﹣10
=0.2m+78(元);
亮亮该月话费为:
188+0.15×(m﹣350)
=188+0.15m﹣52.5
=0.15m+65.5(元);
他们的话费差为(0.2m+78)﹣(0.15m+65.5)
=0.05m+12.5(元)。
答:该月他们的话费差是(0.05m+12.5)元。
(3)150+(118﹣88)÷0.2
=150+30÷0.2
=50+150
=300(分钟)
答:小文的主叫时间是300分钟。
故答案为:102,118;300。
【点评】此题考查的目的是理解掌握单价、数量、总价三者之间的关系及应用,分段计费的方法及应用。
33.(2024 沙坪坝区)如图,ABCD是长方形,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求三角形DFG(阴影部分)的面积。
【答案】20。
【分析】分析题意,由点G是线段FC的中点可知三角形DFG和三角形DCG的面积相等,则只需求出三角形FDC的面积即可;观察图形可知,三角形FDC的面积=梯形EDCB的面积﹣三角形EDF的面积﹣三角形BFC的面积,连接CE,由三角形和梯形的面积公式易得三角形EDC和梯形EDCB的面积,从而求得三角形BCE的面积;再根据F是BE的中点不难求得三角形EDF的面积,且三角形BFC的面积是三角形BCE面积的一半,由此求得三角形BFC的面积,根据第二步中的关系求出三角形FDC的面积,至此便可求得三角形DFG(阴影部分)的面积。
【解答】解:连接CE。
S△EDC=4×10÷2=20
S梯形EDCB=(4+12)×10÷2=80
所以S△BFC=(80﹣20)÷2=30,S△EDF=4×5÷2=10,
所以S阴影=(80﹣30﹣10)÷2=20。
答:三角形DFG(阴影部分)的面积是20。
【点评】此题解答的关键是明确:等底等高的三角形的面积相等,根据三角形的面积公式、梯形的面积公式解答。
34.(2024 渝北区)有一项工程,由甲、乙、丙三个工程队每天轮流做。原计划按甲、乙、丙次序轮流做,恰好整数天完成。如果按乙、丙、甲次序轮做,比原计划多用0.5天;如果按丙、甲、乙次序做,比原计划多用天。已知甲单独做13天完成。且3个工程队的工效各不相同。这项工程由甲、乙、丙合作要多少天完工?
【答案】天。
【分析】据题意可知,按甲、乙、丙次序轮做,恰好整天完工,其余两个方案都不是整天完工,那么甲乙丙的方案,一定是甲或乙结尾,不可能是丙结束,丙结束就是整数周期.所以按两种情况分析:第一种情况是甲结束,甲=乙+丙丙+甲,丙甲,乙甲,这样丙、乙的工作效率就相同了,据题意,三队的工作效率各不相同,从而排除第一种情况;第二种情况,乙结束,甲+乙=乙+丙+甲丙+甲+乙,丙=甲乙,丙=甲,乙=甲,所以三个工程队合作的时间是13÷(1)(天)。
【解答】解:根据条件可从如下两种情况进等分析:
第一种情况是按甲、乙、丙次序轮做,甲结束:
甲=乙+丙丙+甲,丙甲,乙甲,
这样丙、乙的工作效率就相同了,据题意,三队的工作效率各不相同,从而排除第一种情况;
第二种情况是按甲、乙、丙次序轮做,乙结束:
甲+乙=乙+丙+甲丙+甲+乙,丙=甲乙,丙=甲,乙=甲,
所以三个工程队合作的时间是13÷(1)(天)。
答:那么这项工程由甲、乙、丙三个队合作要天完成。
【点评】完成本题要据所给条件分两种情况以甲为1进行认真的分析,从而得出另两个队的工作效率。
35.(2024 渝北区)如图,A、B是一条道路的两端点,亮亮在A点,明明在B点,两人同时出发,相向而行,他们在离A点100米的C点第一次相遇,亮亮到达B点后返回A点,明明到达A点后返回B点,两人在离B点80米的D点第二次相遇。整个过程中,两人各自的速度都保持不变,求A、B间的距离。
【答案】220米。
【分析】从出发到第一次相遇,两人一共走了1个全程,其中亮亮走了100米;第二次相遇时,两人共走了2个全程,其中亮亮走了2个100米,即两人一共走了3个全程,亮亮一共走了3个100米,又因为亮亮从出发到第二次相遇,一共走了1个全程多80米,所以A、B间的距离为:300﹣80,据此计算即可解答。
【解答】解:第一次相遇,两人一共走了1个全程,其中亮亮走了100米;
第二次相遇时,两人共走了2个全程,因为亮亮走(CB+DB)用的时间是2个走AC的时间,所以走的路程也是2个AC,则亮亮走的路程为:CB+DB=2AC=2×100=200(米),
从出发到第二次相遇亮亮一共走的路程为:100+200=300(米),
又因为亮亮从出发到第二次相遇,一共走了1个全程多80米,即A、B间距离+80=300,所以A、B间的距离为:300﹣80=220(米)。
答:A、B间的距离是220米。
【点评】此题考查多次相遇问题。解答本题的关键是理清亮亮在两次相遇过程中走的路程,根据亮亮走的路程找出等量关系,再列式计算。
36.(2024 渝北区)在长方形ABCD中,AB=30cm,BC=40cm,如图P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值。
【答案】24厘米。
【分析】连接OP,三角形OBC的面积就等于长方形的面积的,又由三角形OPB的面积+三角形POC的面积=三角形OBC的面积,且OB=OCDB,于是求出DB的长度,问题即可迎刃而解。
【解答】解:连接OP,如图所示:
因为长方形的面积=40×30=1200 ( cm2)
△OBC的面积1200=300 ( cm2)
又因为DB2=302+402=2500(cm)
所以DB=50cm
所以OB=OC=DB=25cm
25×PR25×PQ=300
即25×(PR+PQ )=300
所以PR+PQ=24 cm
答:PQ+PR的值24厘米。
【点评】本题主要考查组合图形的面积的计算,关键利用长方形和三角形面积的关系计算。
37.(2024 渝北区)底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积.
【答案】见试题解答内容
【分析】由题意可知:阴影部分的面积=大圆的面积+小半圆的面积×2(小圆的面积)﹣三角形的面积,据此代入数据即可求解.
【解答】解:S阴影=S大圆+S半圆×2﹣S三角形
=3.14×(6÷2)2+3.14×(6÷2÷2)2﹣6×6
=3.14×9+3.14×2.25﹣18
=28.26+7.065﹣18
=17.325(平方厘米)
答:阴影部分的面积是17.325平方厘米
【点评】解答此题的主要依据是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求解.
38.(2024 重庆)李师傅加工一批零件,原计划每小时加工30个,6小时可以完成,实际每小时比原计划多加工20%,实际加工这批零件比原计划提前几小时?
【答案】1小时。
【分析】要求实际加工这批零件比原计划提前几小时,就要求出实际加工这批零件用了几小时,因实际每小时比原来计划多加工20%,要把原计划加工的个数看作单位“1”,也就实际每天加工的是原计划每天加工的(1+20%),又因原计划每小时加工30个,可求出实际每天加工的个数.又因原计划每小时加工30个,6小时可以完成,可求出这批零件一共多少个.再根据除法的意义,可求出实际加工这批零件用了多少小时,原计划加工用的时间减去实际加工用的时间即可解答。
【解答】解:30×6=180(个)
30×(1+20%)
=30×1.2
=36(个)
180÷36=5(小时)
6﹣5=1(小时)
答:实际加工这批零件比原计划提前1小时。
【点评】本题综合考查了学生对单位“1”的掌握以及根据乘、除法的意义解答应用题的能力。
39.(2024 九龙坡区)甲容器中有500克20%盐水,乙容器中有500克水,先将甲中一半的盐水到入乙,充分搅拌;在将乙中一半的盐水到入甲,充分搅拌;最后将甲中盐水的一部分倒入乙,使甲、乙的盐水重量相同.求此时乙中盐水的浓度是多少?.
【答案】见试题解答内容
【分析】先把盐水看成2部分,即盐水=盐+水,根据“溶质质量=溶液质量×浓度”,甲容器里的盐可以算出:500×20%=100(克),水:500﹣100=400(克),然后甲乙一半,甲这时50克盐,200克水,乙这时500+200=700克水,50克盐,其次乙中一半的盐水再倒入甲:这时甲75克盐,550克水,浓度75÷(75+550)=75÷625=12%,盐水总质量75+550=625(克);这时乙25克盐,350克水,浓度现在不算,最后算,总质量375克,使甲、乙的盐水重量相同,甲给乙:(625﹣375)÷2=250÷2=125(克),甲倒给乙的盐水中含盐:125×12%=15(克),水:125﹣15=110(克),此时乙中盐水的浓度:100%=8%.
【解答】解:甲容器里的盐:500×20%=100(克)
水:500﹣100=400(克)
甲一半给乙,甲这时50克盐,200克水,乙这时500+200=700(克)水,50克盐
乙中一半的盐水再倒入甲:这时甲75克盐,550克水
浓度75÷(75+550),
=75÷625
=3/25
=12%
盐水总质量75+550=625(克)
这时乙25克盐,350克水,总质量375克
使甲、乙的盐水重量相同,甲给乙:(625﹣375)÷2=250÷2=125(克)
甲倒给乙的盐水中含盐:125×12%=15(克)
水:125﹣15=110(克)
此时乙中盐水的浓度:
100%,
100%,
=8%
答:此时乙中盐水的浓度是8%.
【点评】解答此题关键明白:溶质质量=溶液质量×浓度;溶液混合均匀,倒出体积的一半,其中溶质、溶剂占一半;浓度的意义:浓度指某物种在总量中所占的分量.
40.(2024 长沙)某游乐场在开门前有400人排队等待,开门后每分钟来的人数是固定的.一个入场口每分钟可以进来10个游客,如果开放4个入场口.20分钟就没有人排队,现在开放6个入口,那么开门后多少分钟后就没有人排队?
【答案】见试题解答内容
【分析】此题里有两个不变的量:一是开门前排队人数是固定数,即400人;二是开门后每分钟来的人数是固定的.按开4个入场口的已知条件,可求出开门后每分钟来的人数.然后设开放6个入场口开门后x分钟后没有人排队,可按以下两种方式求出开门后x分钟总进场人数:一是根据每分钟1个入场口进客人数可得开6个入场口x分钟的进场人数;二是根据开门后x每分钟来的固定人数加开门前排队的400人,根据这个等量关系即可列出方程.
【解答】解:4个入场口20分钟进入的人数是:
10×4×20=800(人),
开门后20分钟来的人数是:800﹣400=400(人),
开门后每分钟来的人数是:400÷20=20(人),
设开6个入场口x分钟后没有人排队,由题意列方程得
10×6×x=400+20x,
40x=400,
x=10,
答:开放6个入场口10分钟后就没有人排队.
【点评】关键点:一是由已知条件求出开门后每分钟来的人数;二是根据一个入场口每分钟进客量和开门后每分钟来的人数两种方式求开门后设定时间内进客总量这个等量关系.
41.(2024 江北区)对于任意一个四位数m,其各位数字互不相等,若它的千位数字与百位数字的和等于十位数字与个位数字的和,则称这个四位数m为“天平数”,记F(m)为m的各个数位上的数字之和。例如:m=1432,∵1+4=3+2,∴1432是“天平数”,F(1432)=1+4+3+2=10;m=6397,∵6+3≠9+7,∴6397不是“天平数”。
(1)求出F(5234)的值;
(2)已知M,N均为“天平数”,其中M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数),N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c<9,0≤d≤9,a,b,c,d是整数)。若F(M) F(N)=264,求出满足条件的M的最大值与最小值的差。
【答案】(1)14;(2)3600。
【分析】(1)根据“天平数”的概念可知,5+2=3+4=7,即5234是“天平数”,F(5234)为5234的各个数位上的数字之和,即求5234的数字和即可;
(2)根据“天平数”的概念与已知条件列出方程,再求出符合条件的x、y、b的值便即可解答。
【解答】解:(1)F(5234)=5+2+3+4=14
答:F(5234)的值是14。
(2)因为M“天平数”,M=1000x+100b+320+y,(1≤x≤9,0≤b≤6,0≤y≤9,x,b,y是整数)
所以x+b+3=2+y,F(M)=x+b+3+2+y
所以x+b=y﹣1
因为N是“天平数”,N=2000a+100b+10c+d,(1≤a≤4,0≤b≤6,0≤c≤9,0≤d≤9,a,b,c,d是整数)
所以2a+b=c+d,F(N)=2a+b+c+d
因为F(M) F(N)=264
所以(x+b+3+2+y)(2a+b+c+d)=264
即(y﹣1+3+2+y)(2a+b+2a+b)=264
所以(4+2y)(4a+2b)=264
即(2+y)(2a+b)=66
因为0≤y≤9
所以2≤2+y≤11
因为1≤a≤4,0≤b≤6
所以2≤2a+b≤14
根据66=1×66=2×33=3×22=6×11
所以(2+y)(2a+b)=66=6×11
当时,y=4,b为奇数且0≤b≤6
故b为1或3或5。
因为x+b+3=2+y=6
所以x+b=3
又因为1≤x≤9
所以x=2,b=1
此时a=5,不满足1≤a≤4。
即时,无解。
当时,y=9,b为偶数且0≤b≤6
故b为0或2或4或6
因为x+b+3=2+y=11
所以x+b=8
又因为1≤x≤9
所以x=8,b=0或x=6,b=2或x=4,b=4或x=2,b=6
此时a=3或a=2或a=1或a=0,
又1≤a≤4,所以a=3或a=2或a=1。
即,此时M=1000x+100b+320+y=1000×8+100×0+320+9=8329,即M的值为8329;
或,此时M=1000x+100b+320+y=1000×6+100×2+320+9=6529,即M的值为6529;
或,此时M=1000x+100b+320+y=1000×4+100×4+320+9=4729,即M的值为4729。
综上所述,M的值为8329或6529或4729。
所以Mmax=8329,Mmin=4729
Mmax﹣Mmin=8329﹣4729=3600
答:M的最大值与最小值的差是3600。
【点评】本题考查了新定义,不定方程的解,关键是正确理解新定义,解题关键是根据题意列出方程。
42.(2024 石柱县)中国建筑中经常能见到如图的设计。如果图中圆的面积是6.28m2,那么整个图形中所有空白部分的面积是多少m2?(π取3.14)
【答案】2.28m2。
【分析】空白部分的面积即为圆面积减去小正方形的面积,据此解答。
【解答】解:设圆半径为r,则r2=6.28÷3.14=2(m2)
圆的直径即为小正方形对角线,所以小正方形面积=(2r)2÷2=2r2=2×2=4(m2)
6.28﹣4=2.282(m2)
答:整个图形中所有空白部分的面积是2.28m2。
【点评】本题考查了不规则图形面积计算。
43.(2024 渝北区)如图,最小正方形的边长为单位1,25个这样的小正方形拼成一个大正方形ABCD,其中,有7个最小正方形被涂上了阴影;用S表示剩下的18个最小正方形的面积和。
(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形的可能性为 ;
(2)在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边 AD 上,距离A点 0.2 个单位长度;
(3)甲、乙两个机器人分别从A、C两点开始,同时出发绕着正方形ABCD的边行走,甲以每秒3个单位的速度顺时针行走,乙以每秒2个单位的速度逆时针行走,请计算得出:他们之间的第18次相遇在何时在何地?
【答案】(1);(2)AD,0.2;(3)出发后70秒的C。
【分析】(1)根据图示可知,涂色小正方形共计7个,如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形,则涂色小正方形的位置只有2种可能,用可以涂色的小正方形个数除以空白小正方形的个数即可求出可能性大小;
(2)根据正方形对角线把正方形面积平分可知,三角形ABC中的S部分面积为8.5,而直线CP恰好平分S,则S的一半即为9,故P点在线段AD上,根据“形面积=(上底+下底)×高÷2”即可求出P点离A点的单位长度;
(3)甲、乙两个机器人第1次相遇时走过了正方形周长的一半,从第2次相遇到第18次相遇,每次相遇,两个机器人合走一个正方形周长,据此求出甲乙机器人相遇18次需要走过的路程和,根据“时间=路程和÷速度和”即可求出第18次相遇的时间,即第18次相遇时间;再根据“路程=时间×速度”求出甲机器人在甲乙机器人相遇18次时走过的路程,用甲机器人走过的路程除以正方形的周长,根据余数即可推算第18次相遇时的具体位置,据此解答。
【解答】解:(1)如果在18个未被涂上阴影的最小正方形中任选一个涂上阴影后,剩下17个未被涂阴影的最小正方形恰好是轴对称图形涂色方式只有如下图2种涂色方法,如下图所示:
即可能性为2÷18。
(2)因为最小正方形的边长为单位1,
所以S=18×1×1=18
S18=9
如下图所示,连接正方形ABCD的对角线AC,则△ABC中S部分为25×1×1﹣4×1×1=8.5<9,故P点应在线段AD上,
即P点在线段AD上把正方形ABCD分成一个三角形CDP和一个直角梯形ABCP,且三角形CDP和直角梯形ABCP的S部分面积均为9,
所以S梯形ABCP=9+4=13
因为S梯形ABCP=13(AP+BC)AB(AP+5)×5
所以AP=13×2÷5﹣5=0.2
即点P离点A的距离为0.2个单位。P点位置如下图所示:
所以在线段DA或AB上找个点P,若直线CP恰好平分S,则点P在边AD上,距离A点0.2个单位长度;
(3)甲、乙两个机器人第18次相遇时走过的路程:4×5÷2+4×5×(18﹣1)=350(个单位)
甲、乙两个机器人第18次相遇时间:350÷(3+2)=70(秒)
甲机器人70秒走过的路程:3×70=210(个单位)
正方形周长:4×5=20(个单位)
210÷20=10(圈)……10(个单位)
因为正方形周长为20个单位,甲机器人从A顺时针出发70秒后正好走了10圈10个单位到达C,即甲、乙机器人之间的第18次相遇在出发后70秒的C。
答:甲、乙两个机器人第18次相遇在出发后70秒的C。
故答案为:(1);(2)AD,0.2。
【点评】本题考查了可能性大小问题的应用以及三角形、梯形面积计算的应用以及行程问题的应用,结合图示仔细分析题干不难解答本题。
44.(2024 北碚区)求图中阴影部分的周长和面积(π取3.14)
【答案】18.84厘米;2.28平方厘米。
【分析】如图:
阴影部分的周长等于2个直径是4÷2=2(厘米)的圆的周长加直径是4厘米的圆的周长的一半,据此解答即可。
如图:
通过“割补”的方法,把下面的2个阴影部分分别割补到左面和右面的空白部分,阴影部分的面积等于半径是4÷2=2(厘米)的半圆的面积减去底是4厘米,高是4÷2=2(厘米)的三角形的面积,据此解答即可。
【解答】解:3.14×(4÷2)×2+3.14×4÷2
=12.56+6.28
=18.84(厘米)
3.14×(4÷2)2÷2﹣4×(4÷2)÷2
=6.28﹣4
=2.28(平方厘米)
答:图中阴影部分的周长是18.84厘米,面积是2.28平方厘米。
【点评】本题考查了圆与组合图形周长和面积计算知识,结合题意分析解答即可。
45.(2024 垫江县)1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人,如图。
(1)观察思考,发现规律:每增加1张桌子,可坐人数就增加 2 人。
(2)如果10张餐桌拼在一起,一共可以坐 22 人。
(3)按这样拼下去,m张餐桌可坐 (2m+2) 人。(用含有字母的式子表示)
【答案】(1)2;(2)22;(3)(2m+2)。
【分析】(1)(2)(3)观察可得规律,1张餐桌可坐4人,就是(2×1+2)人,2张餐桌拼在一起可坐(2×2+
同课章节目录
