专题9 构造中位线的方法 (含解析)2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 专题9 构造中位线的方法 (含解析)2024-2025学年北师大版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 00:00:00 | ||
图片预览

文档简介
专题9 构造中位线的方法
母题学大招12 取一边中点构造三角形中位线
1[中]如图,在△ABC 中,延长 BC 至 D,使得 过AC中点 E 作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为 ( )
A.3 B.4
子题练变式
2[中]如图,DE 是△ABC的中位线,F 是 DE 的中点,CF的延长线交AB 于点 G,若△CEF的面积为12cm ,则△DGF的面积为 ( )
B.6cm C.8cm D.9cm
3[中]如图,AD 是△ABC 的中线,M是AD 的中点,连接BM 并延长交AC 于点 N,若AC=4,则AN= .
4[中]如图,在 ABCD中,E是CD的中点,连接AE,BE,F是AE的中点,连接CF 交BE于点G,若BE=8,则GE的长为 .
5[中]如图,在△ABC中,∠C=90°,CA=CB,E,F分别为CA,CB上一点,且CE=CF,M,N分别为AF,BE的中点,求证:
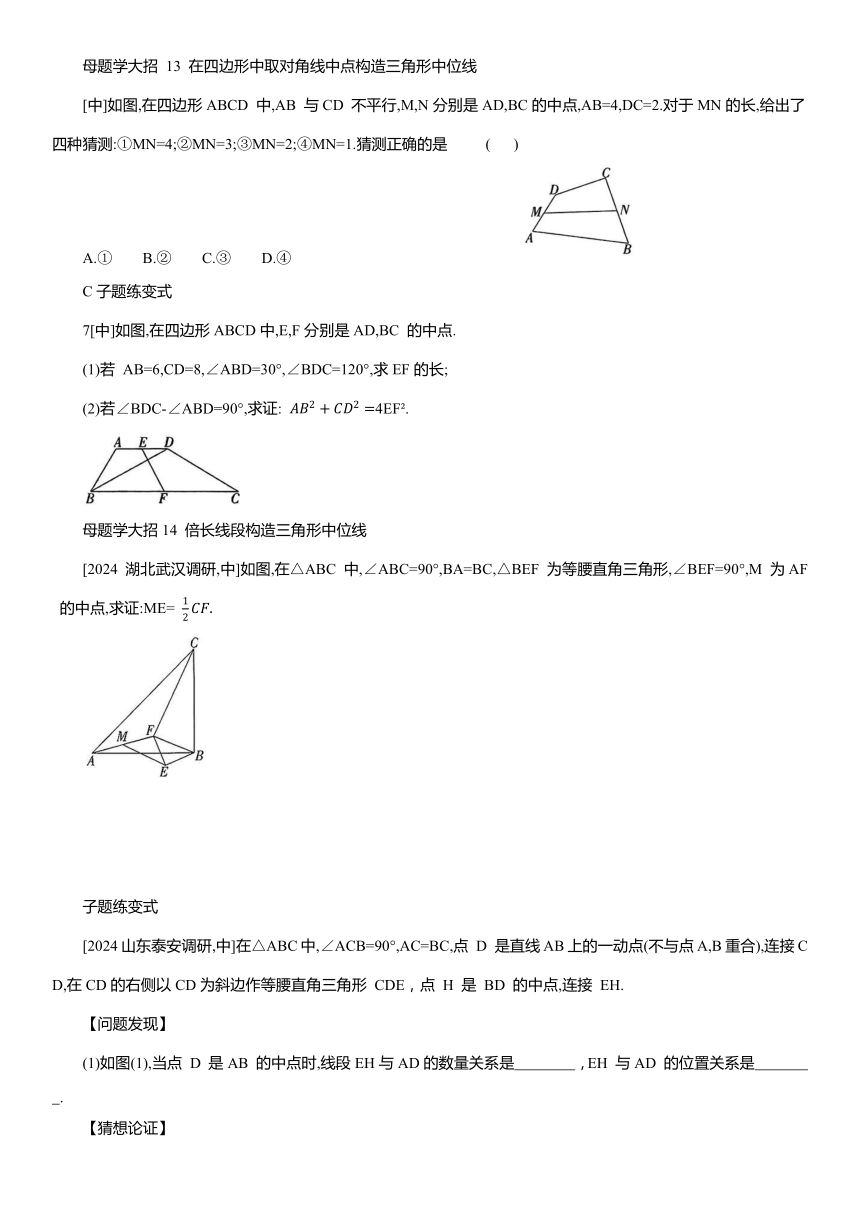
母题学大招 13 在四边形中取对角线中点构造三角形中位线
[中]如图,在四边形ABCD 中,AB 与CD 不平行,M,N分别是AD,BC的中点,AB=4,DC=2.对于MN的长,给出了四种猜测:①MN=4;②MN=3;③MN=2;④MN=1.猜测正确的是 ( )
A.① B.② C.③ D.④
C子题练变式
7[中]如图,在四边形ABCD中,E,F分别是AD,BC 的中点.
(1)若 AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证: 4EF .
母题学大招14 倍长线段构造三角形中位线
[2024 湖北武汉调研,中]如图,在△ABC 中,∠ABC=90°,BA=BC,△BEF 为等腰直角三角形,∠BEF=90°,M 为AF 的中点,求证:ME=
子题练变式
[2024山东泰安调研,中]在△ABC中,∠ACB=90°,AC=BC,点 D 是直线AB上的一动点(不与点A,B重合),连接CD,在CD的右侧以CD为斜边作等腰直角三角形 CDE,点 H 是 BD 的中点,连接 EH.
【问题发现】
(1)如图(1),当点 D 是AB 的中点时,线段EH与AD的数量关系是 ,EH 与AD 的位置关系是 .
【猜想论证】
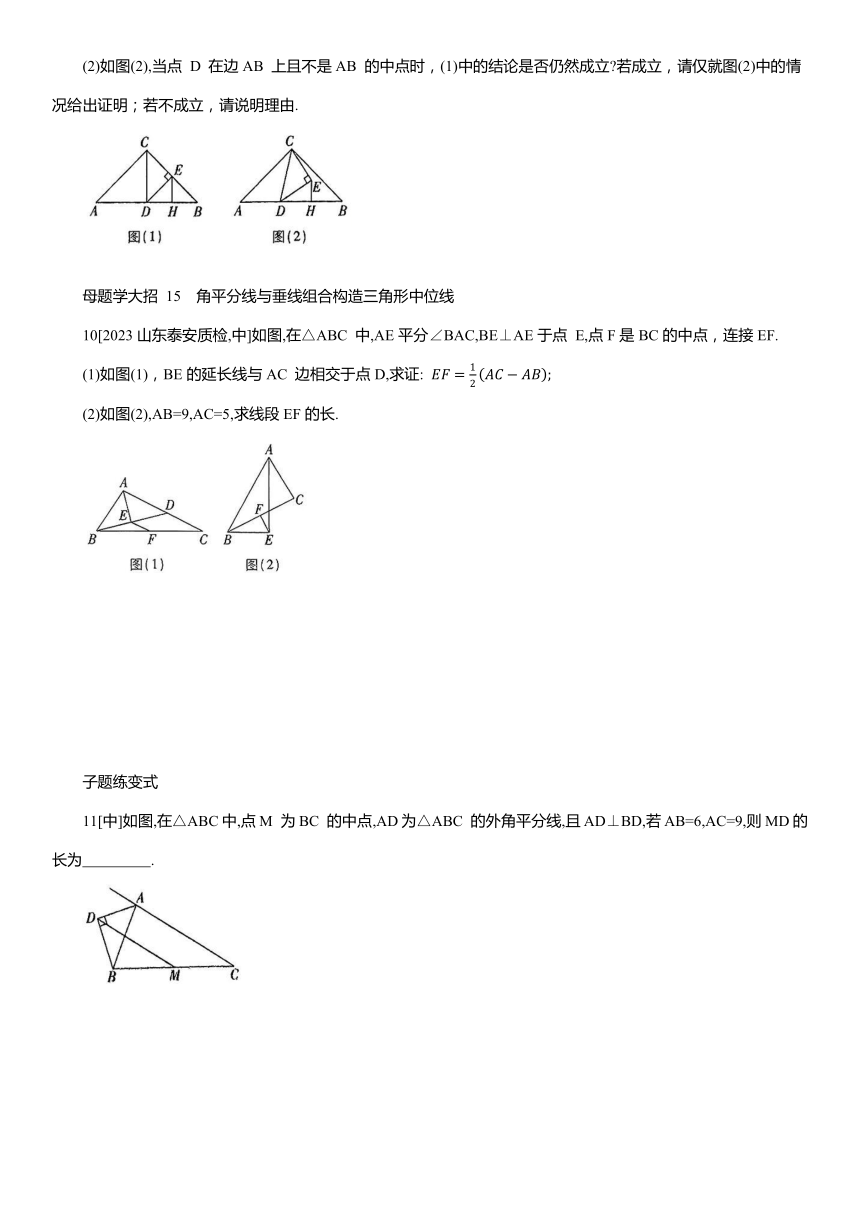
(2)如图(2),当点 D 在边AB 上且不是AB 的中点时,(1)中的结论是否仍然成立 若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
母题学大招 15 角平分线与垂线组合构造三角形中位线
10[2023山东泰安质检,中]如图,在△ABC 中,AE平分∠BAC,BE⊥AE于点 E,点F是BC的中点,连接EF.
(1)如图(1),BE的延长线与AC 边相交于点D,求证:
(2)如图(2),AB=9,AC=5,求线段EF的长.
子题练变式
11[中]如图,在△ABC中,点M 为BC 的中点,AD为△ABC 的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为 .
1. B 【解析】如图,取BC 的中点G,连接EG.∵E 是AC的中点, 设 则 .四边形 EGDF 是平行四边形,∴ 故选 B.
2. A 【解析】如图,取CG的中点H,连接EH.∵E是AC的中点,∴EH 是 的 中 位 线 , ∠HEF.∵F 是DE 的中点,∴DF=EF.又∵ 又∵ 故选A.
【解析】如图,取CN的中点 连接DE.∵ AD 是 的中线, ∴DE∥BN.∵ M 是AD 的中点,∴易知点N为AE中点,∴AN= 故答案为
4.2 【解析】取BE 的中点M,连接FM,CM,如图所示.∵F为AE的中点,M为 BE 的中点,∴MF= 四边形ABCD 是平行四边形,∴ 为CD的中点, FM,∴四边形 EFMC 是平行四边形,∴EG= 故答案为2.
5.【证明】如图,取AB的中点 G,连接MG,NG.∵M,N分别为AF,BE的中点,
CF,AC⊥BC,∴AE=BF,NG⊥ BMG,∴MG= NG,∠MGN=90°,∴△MNG 是等腰直角三角形,.
6. C 【解析】如图,连接BD,取BD的中点G,连接MG,NG.
∵点 M,N 分别是AD,BC 的中点,∴MG 是△ABD 的中位线,NG 是△BCD 的中位线,∴ AB =2MG,DC=2NG.∵ AB =4,DC=2,∴MG=2,NG=1.由三角形三边关系得MG-NG7.(1)【解】如图,取BD的中点P,连接EP,FP.
∵E,F分别是AD,BC的中点,AB=6,CD=8,∴PE∥AB,且 且PF=
又∵ ∠ABD=30°,∠BDC=120°,∴ ∠EPD=∠ABD=30°,∠DPF = 180°-∠BDC = 60°,
∴∠EPF=∠EPD+∠DPF=90°.
在 Rt △EPF 中, 由 勾 股 定 理 得 EF =
(2)【证明】如图,∵E,F分别是AD,BC 的中点,
∴PE∥AB,且 且 PF=
∴∠EPD=∠ABD,∠DPF=180°-∠BDC.
∵∠BDC-∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴ ∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)=90°,
大招解读|倍长线段构造三角形中位线
倍长法是构造三角形中位线的常用方法,即通过作延长线,取倍长线段构造中点.该方法适用于只知道一边中点的情形,同时出现“类中位线”的半缺三角形,此时可以延长线段,设定中点,构建出中位线对应的三角形.
模型特征 操作方法
条件:已知 D 是 AB 边的中点; 辅助线:延长AC 到E,使CE=AC,连接BE(也可倍长BC); 结论:DC∥BE,DC= BE
8.【证明】如图,延长 FE 到D, 使 DE = EF, 连 接AD,BD.
∵△BEF为等腰直角三角形,∠BEF=90°,
∴ ∠BFE=45°,BE⊥DF,
∴BE 垂直平分DF,
∴BD=BF,∴ ∠BDE=45°,∴ ∠DBF=90°,
∴△BDF 是等腰直角三角形.
∵ ∠CBF +∠ABF = ∠ABC = 90°, ∠ABD +∠ABF=∠DBF=90°,∴∠CBF=∠ABD.
在△ABD和△CBF中,
∴△ABD≌△CBF(SAS),∴AD=CF.
∵M 为AF 的中点,DE=EF,∴ ME 是△ADF的中位线,
9.【解】(1)∵CA=CB,∠ACB=90°,AD=BD,∴CD⊥AB,∠A=∠B=45°,∠ACD=∠BCD=45°,∴CD=AD=DB.∵△CDE 是等腰直角三角形,CD为斜边,∴∠DCE=45°,∴点 E 在线段 CB 上.∵ DE⊥BC,∴∠EDB=∠B=45°,∴DE=BE.∵DH=HB,∴EH⊥DB,∠DEH= 故答案为
(2)结论仍然成立.理由:如图,延长DE到 F,使得EF= DE,连接 CF,BF.∵ DE = EF,CE⊥DF,△CDE是等腰直角三角形,∴ CD = CF,∴∠CDF=∠CFD =45°,∠ECF = ∠ECD =45°,∴∠ACB=∠DCF=90°,∴∠ACD=∠BCF.又∵CA=CB,∴△ACD≌△BCF(SAS),
∴AD=BF,∠A=∠CBF=45°.
∵∠ABC=45°,∴∠ABF=90°,∴BF⊥AB.
10.(1)【证明】∵AE平分∠BAC,
∴∠BAE=∠DAE.
∵BE⊥AE,∴∠AEB=∠AED=90°.
在 和 中
∴BE=ED,AD=AB.
∵BF=FC,
(2)【解】如图,分别延长BE,AC交于点H.
同(1)可证明△ABE≌△AHE,
∴BE=EH,AH=AB=9.
11.7.5 【解析】如图,延长 E:BD 交CA 的延长线于 E.∵AD为∠BAE的平分线,BD⊥AD,∴∠EAD=∠BAD, AC+AE=9+6=15.又∵M 为 BC 的中点,∴DM 是△BCE 的中位线, 故答案为7.5.
母题学大招12 取一边中点构造三角形中位线
1[中]如图,在△ABC 中,延长 BC 至 D,使得 过AC中点 E 作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为 ( )
A.3 B.4
子题练变式
2[中]如图,DE 是△ABC的中位线,F 是 DE 的中点,CF的延长线交AB 于点 G,若△CEF的面积为12cm ,则△DGF的面积为 ( )
B.6cm C.8cm D.9cm
3[中]如图,AD 是△ABC 的中线,M是AD 的中点,连接BM 并延长交AC 于点 N,若AC=4,则AN= .
4[中]如图,在 ABCD中,E是CD的中点,连接AE,BE,F是AE的中点,连接CF 交BE于点G,若BE=8,则GE的长为 .
5[中]如图,在△ABC中,∠C=90°,CA=CB,E,F分别为CA,CB上一点,且CE=CF,M,N分别为AF,BE的中点,求证:
母题学大招 13 在四边形中取对角线中点构造三角形中位线
[中]如图,在四边形ABCD 中,AB 与CD 不平行,M,N分别是AD,BC的中点,AB=4,DC=2.对于MN的长,给出了四种猜测:①MN=4;②MN=3;③MN=2;④MN=1.猜测正确的是 ( )
A.① B.② C.③ D.④
C子题练变式
7[中]如图,在四边形ABCD中,E,F分别是AD,BC 的中点.
(1)若 AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证: 4EF .
母题学大招14 倍长线段构造三角形中位线
[2024 湖北武汉调研,中]如图,在△ABC 中,∠ABC=90°,BA=BC,△BEF 为等腰直角三角形,∠BEF=90°,M 为AF 的中点,求证:ME=
子题练变式
[2024山东泰安调研,中]在△ABC中,∠ACB=90°,AC=BC,点 D 是直线AB上的一动点(不与点A,B重合),连接CD,在CD的右侧以CD为斜边作等腰直角三角形 CDE,点 H 是 BD 的中点,连接 EH.
【问题发现】
(1)如图(1),当点 D 是AB 的中点时,线段EH与AD的数量关系是 ,EH 与AD 的位置关系是 .
【猜想论证】
(2)如图(2),当点 D 在边AB 上且不是AB 的中点时,(1)中的结论是否仍然成立 若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
母题学大招 15 角平分线与垂线组合构造三角形中位线
10[2023山东泰安质检,中]如图,在△ABC 中,AE平分∠BAC,BE⊥AE于点 E,点F是BC的中点,连接EF.
(1)如图(1),BE的延长线与AC 边相交于点D,求证:
(2)如图(2),AB=9,AC=5,求线段EF的长.
子题练变式
11[中]如图,在△ABC中,点M 为BC 的中点,AD为△ABC 的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为 .
1. B 【解析】如图,取BC 的中点G,连接EG.∵E 是AC的中点, 设 则 .四边形 EGDF 是平行四边形,∴ 故选 B.
2. A 【解析】如图,取CG的中点H,连接EH.∵E是AC的中点,∴EH 是 的 中 位 线 , ∠HEF.∵F 是DE 的中点,∴DF=EF.又∵ 又∵ 故选A.
【解析】如图,取CN的中点 连接DE.∵ AD 是 的中线, ∴DE∥BN.∵ M 是AD 的中点,∴易知点N为AE中点,∴AN= 故答案为
4.2 【解析】取BE 的中点M,连接FM,CM,如图所示.∵F为AE的中点,M为 BE 的中点,∴MF= 四边形ABCD 是平行四边形,∴ 为CD的中点, FM,∴四边形 EFMC 是平行四边形,∴EG= 故答案为2.
5.【证明】如图,取AB的中点 G,连接MG,NG.∵M,N分别为AF,BE的中点,
CF,AC⊥BC,∴AE=BF,NG⊥ BMG,∴MG= NG,∠MGN=90°,∴△MNG 是等腰直角三角形,.
6. C 【解析】如图,连接BD,取BD的中点G,连接MG,NG.
∵点 M,N 分别是AD,BC 的中点,∴MG 是△ABD 的中位线,NG 是△BCD 的中位线,∴ AB =2MG,DC=2NG.∵ AB =4,DC=2,∴MG=2,NG=1.由三角形三边关系得MG-NG
∵E,F分别是AD,BC的中点,AB=6,CD=8,∴PE∥AB,且 且PF=
又∵ ∠ABD=30°,∠BDC=120°,∴ ∠EPD=∠ABD=30°,∠DPF = 180°-∠BDC = 60°,
∴∠EPF=∠EPD+∠DPF=90°.
在 Rt △EPF 中, 由 勾 股 定 理 得 EF =
(2)【证明】如图,∵E,F分别是AD,BC 的中点,
∴PE∥AB,且 且 PF=
∴∠EPD=∠ABD,∠DPF=180°-∠BDC.
∵∠BDC-∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴ ∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)=90°,
大招解读|倍长线段构造三角形中位线
倍长法是构造三角形中位线的常用方法,即通过作延长线,取倍长线段构造中点.该方法适用于只知道一边中点的情形,同时出现“类中位线”的半缺三角形,此时可以延长线段,设定中点,构建出中位线对应的三角形.
模型特征 操作方法
条件:已知 D 是 AB 边的中点; 辅助线:延长AC 到E,使CE=AC,连接BE(也可倍长BC); 结论:DC∥BE,DC= BE
8.【证明】如图,延长 FE 到D, 使 DE = EF, 连 接AD,BD.
∵△BEF为等腰直角三角形,∠BEF=90°,
∴ ∠BFE=45°,BE⊥DF,
∴BE 垂直平分DF,
∴BD=BF,∴ ∠BDE=45°,∴ ∠DBF=90°,
∴△BDF 是等腰直角三角形.
∵ ∠CBF +∠ABF = ∠ABC = 90°, ∠ABD +∠ABF=∠DBF=90°,∴∠CBF=∠ABD.
在△ABD和△CBF中,
∴△ABD≌△CBF(SAS),∴AD=CF.
∵M 为AF 的中点,DE=EF,∴ ME 是△ADF的中位线,
9.【解】(1)∵CA=CB,∠ACB=90°,AD=BD,∴CD⊥AB,∠A=∠B=45°,∠ACD=∠BCD=45°,∴CD=AD=DB.∵△CDE 是等腰直角三角形,CD为斜边,∴∠DCE=45°,∴点 E 在线段 CB 上.∵ DE⊥BC,∴∠EDB=∠B=45°,∴DE=BE.∵DH=HB,∴EH⊥DB,∠DEH= 故答案为
(2)结论仍然成立.理由:如图,延长DE到 F,使得EF= DE,连接 CF,BF.∵ DE = EF,CE⊥DF,△CDE是等腰直角三角形,∴ CD = CF,∴∠CDF=∠CFD =45°,∠ECF = ∠ECD =45°,∴∠ACB=∠DCF=90°,∴∠ACD=∠BCF.又∵CA=CB,∴△ACD≌△BCF(SAS),
∴AD=BF,∠A=∠CBF=45°.
∵∠ABC=45°,∴∠ABF=90°,∴BF⊥AB.
10.(1)【证明】∵AE平分∠BAC,
∴∠BAE=∠DAE.
∵BE⊥AE,∴∠AEB=∠AED=90°.
在 和 中
∴BE=ED,AD=AB.
∵BF=FC,
(2)【解】如图,分别延长BE,AC交于点H.
同(1)可证明△ABE≌△AHE,
∴BE=EH,AH=AB=9.
11.7.5 【解析】如图,延长 E:BD 交CA 的延长线于 E.∵AD为∠BAE的平分线,BD⊥AD,∴∠EAD=∠BAD, AC+AE=9+6=15.又∵M 为 BC 的中点,∴DM 是△BCE 的中位线, 故答案为7.5.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
