6.4多边形的内角和与外角和 同步练习(含解析)2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 6.4多边形的内角和与外角和 同步练习(含解析)2024-2025学年北师大版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 222.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 22:50:45 | ||
图片预览



文档简介
6.4多边形的内角和与外角和
课时1 多边形的内角和
刷基础
知识点1 多边形与三角形的关系
1从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①②表示的数字,正确的是 ( )
A.①6;②7 B.①7;②8
C.①8;②8 D.①9;②7
2过m边形的一个顶点能作7条对角线,并将m边形分成b个三角形,n边形没有对角线,k边形有k条对角线,则
知识点2 与多边形内角和有关的计算
3[2024 山东海阳期中]如图,则x的值为( )
A.100 B.120 C.122 D.150
4[2024 河南周口质检]五边形 ABCDE 的各边所在直线形成如图所示的形状,则∠1+∠2+∠3+∠4+∠5+∠6= ( )
A.180° B.270° C.360° D.540°
5[2023江苏泰州期中]将一个多边形切去一个角后所得的多边形内角和为2 880°,则原多边形的边数为 ( )
A.15或16 B.15或16或17
C.16或17或18 D.17或18或19
6通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 °.
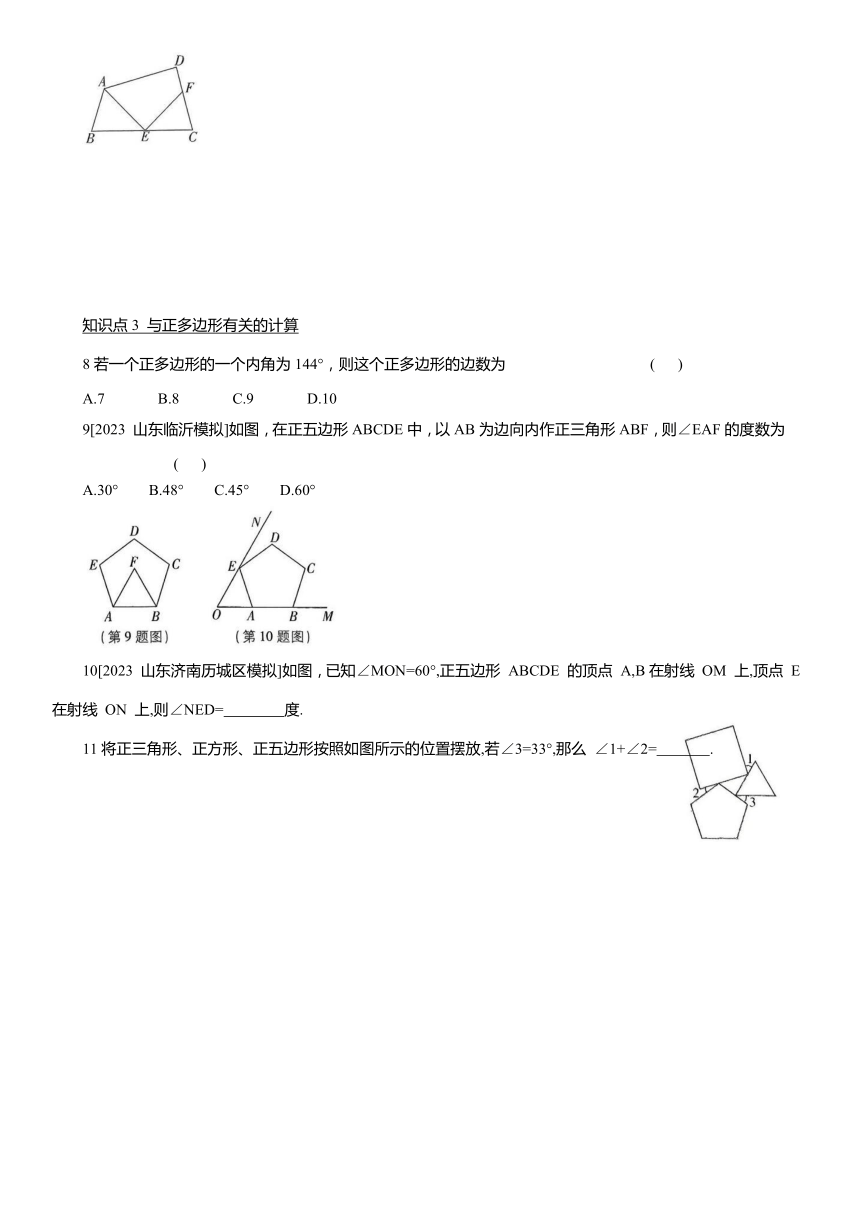
7如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点 F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明∠B=∠C.
知识点3 与正多边形有关的计算
8若一个正多边形的一个内角为144°,则这个正多边形的边数为 ( )
A.7 B.8 C.9 D.10
9[2023 山东临沂模拟]如图,在正五边形ABCDE中,以AB为边向内作正三角形ABF,则∠EAF的度数为 ( )
A.30° B.48° C.45° D.60°
10[2023 山东济南历城区模拟]如图,已知∠MON=60°,正五边形 ABCDE 的顶点 A,B在射线 OM 上,顶点 E 在射线 ON 上,则∠NED= 度.
11将正三角形、正方形、正五边形按照如图所示的位置摆放,若∠3=33°,那么 ∠1+∠2= .
课时2 多边形的外角和
刷基础
知识点1 多边形的外角和
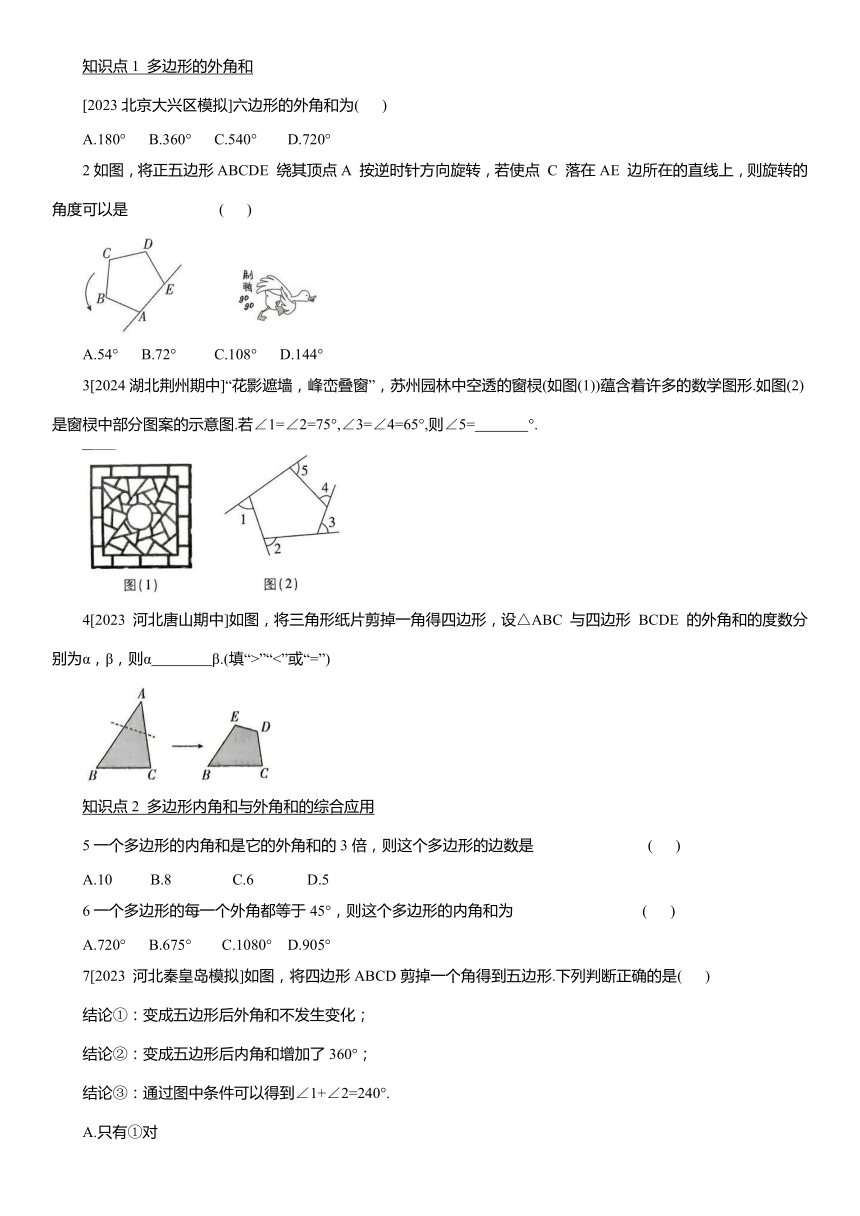
[2023北京大兴区模拟]六边形的外角和为( )
A.180° B.360° C.540° D.720°
2如图,将正五边形ABCDE 绕其顶点A 按逆时针方向旋转,若使点 C 落在AE 边所在的直线上,则旋转的角度可以是 ( )
A.54° B.72° C.108° D.144°
3[2024湖北荆州期中]“花影遮墙,峰峦叠窗”,苏州园林中空透的窗棂(如图(1))蕴含着许多的数学图形.如图(2)是窗棂中部分图案的示意图.若∠1=∠2=75°,∠3=∠4=65°,则∠5= °.
4[2023 河北唐山期中]如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形 BCDE 的外角和的度数分别为α,β,则α β.(填“>”“<”或“=”)
知识点2 多边形内角和与外角和的综合应用
5一个多边形的内角和是它的外角和的3倍,则这个多边形的边数是 ( )
A.10 B.8 C.6 D.5
6一个多边形的每一个外角都等于45°,则这个多边形的内角和为 ( )
A.720° B.675° C.1080° D.905°
7[2023 河北秦皇岛模拟]如图,将四边形ABCD剪掉一个角得到五边形.下列判断正确的是( )
结论①:变成五边形后外角和不发生变化;
结论②:变成五边形后内角和增加了360°;
结论③:通过图中条件可以得到∠1+∠2=240°.
A.只有①对
B.①和③对
C.①②③都对
D.①②③都不对
8一个多边形的外角和比内角和小180°,则这个多边形是 边形.
9[2024山东临沂期中]阅读小明和小红的对话,解决下列问题:
(1)通过列方程说明“多边形的内角和不可能是1470°”的理由;
(2)求该多边形的内角和;
(3)若这是个正多边形,求该正多边形的一个内角比一个外角大多少.
刷提升
1[2024山东烟台期末,中]一机器人在平地上按如图设置的程序行走,则该机器人从开始到结束共行走的路程为 ( )
A.24m B.28m C.32m D.36m
[2023 河北唐山模拟,中]如图,以正六边形ABCDEF的对角线BD为边,向右作等边三角形BDG,若四边形BCDG(图中阴影部分)的面积为6,则五边形ABDEF 的面积为 ( )
A.15 B.12 C.8 D.6
3[2023 广东梅州调研,中]如图,正 n 边形 (每条边相等,每个内角都相等)竖立于地面,一边与地面重合,一束太阳光平行照射在正 n 边形上,若∠1-∠2= 36°,则n= .
4[中]如图,在正六边形ABCDEF 的内部作正五边形 DEMGH.
(1)∠CDH= °;
(2)连接EG并延长,交AB 于点 N,则∠ANE= °.
5[2024吉林长春期中,中]如图,用n个全等的正五边形按如图方式拼成一个环状图形,相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前 3 个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为 .
2刷素养 走向重高
6 核心素养推理能力[2024 山西朔州校级质检,较难]将纸片△ABC 沿 DE 折叠使点 A 落在点A'处.
【感知】如图(1),点A 落在四边形 BCDE 的边BE 上,则∠A 与∠1 之间的数量关系是
【探究】如图(2),若点 A 落在四边形 BCDE 的内部,则∠A 与∠1+∠2之间存在怎样的数量关系 并说明理由.
【拓展】如图(3),点A 落在四边形 BCDE 的外部,若∠1=80°,∠2=24°,则∠A 的大小为
4 多边形的内角和与外角和
课时1 多边形的内角和
刷基础
1. A 【解析】从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即可以作6条对角线,它们将九边形分成7个三角形.故选A.
2.133 【解析】∵a(a是大于等于3的自然数)边形从一个顶点发出的对角线有(a-3)条,五边形有5条对角线,. 故答案为133.
3. B 【解析】∵五边形的内角和是 解得 故选B.
4. C 【解析】如图所示,∵∠1+∠5=∠8,∠4+ 故选C.
5. D
识图解题
【解析】多边形的内角和可以表示成(n-2).180°(n≥3且n是整数),一个多边形切去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.设切去一个角后所得多边形的边数为n.根据题意得180°(n-2)=2880°,解得n=18,则原多边形的边数可能是17或18或19.故选 D.
6.1 800 【解析】∵从多边形的一个顶点出发的对角线共有(n-3)条,∴n-3=9,解得n=12,∴该多边形的边数是12,∴其内角和为(12-2)×180°=1 800°.故答案为1 800.
7.【解】(1)∵EF⊥AE,∴∠AEF=90°.
∵四边形AEFD的内角和是360°,∠D=90°,∠EAD=60°,∴ ∠DFE=360°-∠D-∠EAD-∠AEF=120°.
(2)∵四边形AEFD的内角和是360°,∠AEF=90°,∠D=90°,
∴∠EAD+∠DFE=180°.
∵∠DFE+∠CFE=180°,
∴∠EAD=∠CFE.
∵AE平分∠BAD,
∴∠BAE=∠EAD,
∴∠BAE=∠CFE.
∵ ∠B+∠BAE+∠AEB=180°,∠C+∠CFE+∠CEF=180°,∠AEB=∠CEF,
∴∠B=∠C.
8. D 【解析】设这个正多边形的边数为 n.根据题意得(n-2)×180°=144°×n,∴ n=10. 故选 D.
9. B 【解析】∵五边形ABCDE 是正五边形, 是等边三角形,∴ ∠FAB=60°,∴ ∠EAF=∠EAB-∠FAB=48°.故选 B.
10.24 【解析】∵五边形ABCDE 是正五边形, 是△AEO 的外角,∴∠AEO=∠EAB-∠MON=108°-60°=48°,∴ ∠NED=180°-∠AEO-∠AED=180°-48°-108°=24°.故答案为24.
11.69° 【解析】如图.∵∠3=33°,正三角形的一个内角是60°,正方形的一个内角是90°,正五边形的一个内角是108°,∴∠4=180°-60°-33°=87°,∴∠5+∠6=180°-87°=93°.∵∠5=180°-∠2-108°=72°-∠2,① ∠6=180°-90°-∠1=90°-∠1,② ∴①+②得72°-∠2+90°-∠1=93°,即∠1+∠2=69°.故答案为69°.
刷基础
1. B 【解析】∵ 多边形的外角和都等于360°,∴六边形的外角和为360°.故选 B.
2. C 【解析】如图,连接AC.在正五边形ABCDE中, ∵∠BAF=360°÷ 5=72°,∴∠CAF=∠CAB+∠BAF=36°+72°=108°,∴若点 C落在AE边所在的直线上,则旋转的角度可以是108°.故选C.
3.80 【解析】∵∠1+∠2+∠3+∠4+∠5=360°,∴∠5=360°-75°-75°-65°-65°=80°,故答案为80.
4.= 【解析】∵任意多边形的外角和为360°,∴α=β=360°,故答案为=.
5. B 【解析】设这个多边形是n边形.由题意得(n-2)·180°=3×360°,解得n=8.故选 B.
6. C 【解析】∵ 多边形的每一个外角都是45°,
∴这个多边形的边数为 ∴这个多边形的内角和为(8-2)×180°=1080°.故选C.
B
8.五 【解析】∵多边形的外角和是360°,∴这个多边形的内角和是360°+180°=540°.设这个多边形的边数为n,则(n-2)×180°=540°,解得n=5,即这个多边形是五边形,故答案为五.
9.【解】(1)设多边形的边数为n,则 180°×(n-2)=1470°,解得
∵n为正整数,∴ 多边形的内角和不可能为1470°.
(2)由题意可知,该多边形的边数为10,∴该多边形的内角和为180°×(10-2)=1440°.
(3)1 440°÷10-360°÷10=144°-36°=108°.
答:该正多边形的一个内角比一个外角大108°.
刷提升
1. C 【解析】由题意得,机器人行走的路径是一个正多边形,∴该机器人从开始到结束共行走的路程为 故选 C
2. A 【解析】如图,连接GC并延长交BD 于点H,连接AE.∵六边形ABCDEF 是正六边形,∴AB=BC=CD=DE=EF=AF,∠F = ∠FAB = ∠ABC =∠BCD =∠CDE=∠DEF=120°.∵△BDG是等边三角形,∴BG=DG=BD.又∵CG=CG,∴△BCG≌△DCG(SSS),∴∠BGC=∠DGC=30°.∵ 易得∠GBC = ∠DBC = 30°,∴ △GBC ≌△DBC 3.设CH=x,则 即 五边形ABDEF的面积为3+12=15.故选A.
3.5 【解析】如图,过 作 则∠4= ∵∠1 - ∠2 = 36°, 设正多边形的一个内角为x,则∠4=180°-x,∴x=36°+∠3,∴∠3=x-36°,∴180°-x=x-36°,解得x=108°,∴ ∠4= 这个正多边形的边数为360°÷ 72°=5,故答案为5.
4.(1)12 (2)72 【解析】(1)∵正六边形的一个内角为 正五边形的一个内角为 ∴∠CDH=∠CDE-∠HDE=120°-108°=12°,故答案为12.(2)由(1)得∠CDH=12°,同理可证∠FEM=12°.∵∠M=108°,MG=ME, ∴ ∠FEN=∠FEM+∠MEG=12°+36°=48°.在四边形ANEF 中,∠A+∠F+∠FEN+∠ANE=360°,∴∠ANE=360°-120°-120°-48°=72°,故答案为72.
5.6 【解析】∵正五边形的外角和为360°,∴正五边形每个外角的度数为360°÷ 5=72°,∴正五边形每个内角为180°-72°=108°,∴拼接一圈后,中间正多边形的每个内角为360°-2× 解得n=6.故答案为6.
刷素养·
6.【解】(1)由折叠可得,∠EA'D=∠A.∵∠1=∠A+∠EA'D,∴ ∠1=2∠A.故答案为∠1=2∠A.
(2)2∠A=∠1+∠2.理由如下:
∵∠1+∠A'DA+∠2+∠A'EA=360°,∠A+ ∠1+∠2.由折叠可得∠A=∠A',∴2∠A=∠1+∠2.
(3)如图,由折叠可得∠A=∠A'.∵ ∠1=∠DFA+∠A,∠DFA=∠A'+∠2,∴ ∠1=∠A+∠A'+∠2=2∠A+∠2,∴2∠A=∠1-∠2=56°,∴∠A=28°.故答案为28°.
课时1 多边形的内角和
刷基础
知识点1 多边形与三角形的关系
1从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①②表示的数字,正确的是 ( )
A.①6;②7 B.①7;②8
C.①8;②8 D.①9;②7
2过m边形的一个顶点能作7条对角线,并将m边形分成b个三角形,n边形没有对角线,k边形有k条对角线,则
知识点2 与多边形内角和有关的计算
3[2024 山东海阳期中]如图,则x的值为( )
A.100 B.120 C.122 D.150
4[2024 河南周口质检]五边形 ABCDE 的各边所在直线形成如图所示的形状,则∠1+∠2+∠3+∠4+∠5+∠6= ( )
A.180° B.270° C.360° D.540°
5[2023江苏泰州期中]将一个多边形切去一个角后所得的多边形内角和为2 880°,则原多边形的边数为 ( )
A.15或16 B.15或16或17
C.16或17或18 D.17或18或19
6通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 °.
7如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点 F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明∠B=∠C.
知识点3 与正多边形有关的计算
8若一个正多边形的一个内角为144°,则这个正多边形的边数为 ( )
A.7 B.8 C.9 D.10
9[2023 山东临沂模拟]如图,在正五边形ABCDE中,以AB为边向内作正三角形ABF,则∠EAF的度数为 ( )
A.30° B.48° C.45° D.60°
10[2023 山东济南历城区模拟]如图,已知∠MON=60°,正五边形 ABCDE 的顶点 A,B在射线 OM 上,顶点 E 在射线 ON 上,则∠NED= 度.
11将正三角形、正方形、正五边形按照如图所示的位置摆放,若∠3=33°,那么 ∠1+∠2= .
课时2 多边形的外角和
刷基础
知识点1 多边形的外角和
[2023北京大兴区模拟]六边形的外角和为( )
A.180° B.360° C.540° D.720°
2如图,将正五边形ABCDE 绕其顶点A 按逆时针方向旋转,若使点 C 落在AE 边所在的直线上,则旋转的角度可以是 ( )
A.54° B.72° C.108° D.144°
3[2024湖北荆州期中]“花影遮墙,峰峦叠窗”,苏州园林中空透的窗棂(如图(1))蕴含着许多的数学图形.如图(2)是窗棂中部分图案的示意图.若∠1=∠2=75°,∠3=∠4=65°,则∠5= °.
4[2023 河北唐山期中]如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形 BCDE 的外角和的度数分别为α,β,则α β.(填“>”“<”或“=”)
知识点2 多边形内角和与外角和的综合应用
5一个多边形的内角和是它的外角和的3倍,则这个多边形的边数是 ( )
A.10 B.8 C.6 D.5
6一个多边形的每一个外角都等于45°,则这个多边形的内角和为 ( )
A.720° B.675° C.1080° D.905°
7[2023 河北秦皇岛模拟]如图,将四边形ABCD剪掉一个角得到五边形.下列判断正确的是( )
结论①:变成五边形后外角和不发生变化;
结论②:变成五边形后内角和增加了360°;
结论③:通过图中条件可以得到∠1+∠2=240°.
A.只有①对
B.①和③对
C.①②③都对
D.①②③都不对
8一个多边形的外角和比内角和小180°,则这个多边形是 边形.
9[2024山东临沂期中]阅读小明和小红的对话,解决下列问题:
(1)通过列方程说明“多边形的内角和不可能是1470°”的理由;
(2)求该多边形的内角和;
(3)若这是个正多边形,求该正多边形的一个内角比一个外角大多少.
刷提升
1[2024山东烟台期末,中]一机器人在平地上按如图设置的程序行走,则该机器人从开始到结束共行走的路程为 ( )
A.24m B.28m C.32m D.36m
[2023 河北唐山模拟,中]如图,以正六边形ABCDEF的对角线BD为边,向右作等边三角形BDG,若四边形BCDG(图中阴影部分)的面积为6,则五边形ABDEF 的面积为 ( )
A.15 B.12 C.8 D.6
3[2023 广东梅州调研,中]如图,正 n 边形 (每条边相等,每个内角都相等)竖立于地面,一边与地面重合,一束太阳光平行照射在正 n 边形上,若∠1-∠2= 36°,则n= .
4[中]如图,在正六边形ABCDEF 的内部作正五边形 DEMGH.
(1)∠CDH= °;
(2)连接EG并延长,交AB 于点 N,则∠ANE= °.
5[2024吉林长春期中,中]如图,用n个全等的正五边形按如图方式拼成一个环状图形,相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前 3 个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为 .
2刷素养 走向重高
6 核心素养推理能力[2024 山西朔州校级质检,较难]将纸片△ABC 沿 DE 折叠使点 A 落在点A'处.
【感知】如图(1),点A 落在四边形 BCDE 的边BE 上,则∠A 与∠1 之间的数量关系是
【探究】如图(2),若点 A 落在四边形 BCDE 的内部,则∠A 与∠1+∠2之间存在怎样的数量关系 并说明理由.
【拓展】如图(3),点A 落在四边形 BCDE 的外部,若∠1=80°,∠2=24°,则∠A 的大小为
4 多边形的内角和与外角和
课时1 多边形的内角和
刷基础
1. A 【解析】从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即可以作6条对角线,它们将九边形分成7个三角形.故选A.
2.133 【解析】∵a(a是大于等于3的自然数)边形从一个顶点发出的对角线有(a-3)条,五边形有5条对角线,. 故答案为133.
3. B 【解析】∵五边形的内角和是 解得 故选B.
4. C 【解析】如图所示,∵∠1+∠5=∠8,∠4+ 故选C.
5. D
识图解题
【解析】多边形的内角和可以表示成(n-2).180°(n≥3且n是整数),一个多边形切去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.设切去一个角后所得多边形的边数为n.根据题意得180°(n-2)=2880°,解得n=18,则原多边形的边数可能是17或18或19.故选 D.
6.1 800 【解析】∵从多边形的一个顶点出发的对角线共有(n-3)条,∴n-3=9,解得n=12,∴该多边形的边数是12,∴其内角和为(12-2)×180°=1 800°.故答案为1 800.
7.【解】(1)∵EF⊥AE,∴∠AEF=90°.
∵四边形AEFD的内角和是360°,∠D=90°,∠EAD=60°,∴ ∠DFE=360°-∠D-∠EAD-∠AEF=120°.
(2)∵四边形AEFD的内角和是360°,∠AEF=90°,∠D=90°,
∴∠EAD+∠DFE=180°.
∵∠DFE+∠CFE=180°,
∴∠EAD=∠CFE.
∵AE平分∠BAD,
∴∠BAE=∠EAD,
∴∠BAE=∠CFE.
∵ ∠B+∠BAE+∠AEB=180°,∠C+∠CFE+∠CEF=180°,∠AEB=∠CEF,
∴∠B=∠C.
8. D 【解析】设这个正多边形的边数为 n.根据题意得(n-2)×180°=144°×n,∴ n=10. 故选 D.
9. B 【解析】∵五边形ABCDE 是正五边形, 是等边三角形,∴ ∠FAB=60°,∴ ∠EAF=∠EAB-∠FAB=48°.故选 B.
10.24 【解析】∵五边形ABCDE 是正五边形, 是△AEO 的外角,∴∠AEO=∠EAB-∠MON=108°-60°=48°,∴ ∠NED=180°-∠AEO-∠AED=180°-48°-108°=24°.故答案为24.
11.69° 【解析】如图.∵∠3=33°,正三角形的一个内角是60°,正方形的一个内角是90°,正五边形的一个内角是108°,∴∠4=180°-60°-33°=87°,∴∠5+∠6=180°-87°=93°.∵∠5=180°-∠2-108°=72°-∠2,① ∠6=180°-90°-∠1=90°-∠1,② ∴①+②得72°-∠2+90°-∠1=93°,即∠1+∠2=69°.故答案为69°.
刷基础
1. B 【解析】∵ 多边形的外角和都等于360°,∴六边形的外角和为360°.故选 B.
2. C 【解析】如图,连接AC.在正五边形ABCDE中, ∵∠BAF=360°÷ 5=72°,∴∠CAF=∠CAB+∠BAF=36°+72°=108°,∴若点 C落在AE边所在的直线上,则旋转的角度可以是108°.故选C.
3.80 【解析】∵∠1+∠2+∠3+∠4+∠5=360°,∴∠5=360°-75°-75°-65°-65°=80°,故答案为80.
4.= 【解析】∵任意多边形的外角和为360°,∴α=β=360°,故答案为=.
5. B 【解析】设这个多边形是n边形.由题意得(n-2)·180°=3×360°,解得n=8.故选 B.
6. C 【解析】∵ 多边形的每一个外角都是45°,
∴这个多边形的边数为 ∴这个多边形的内角和为(8-2)×180°=1080°.故选C.
B
8.五 【解析】∵多边形的外角和是360°,∴这个多边形的内角和是360°+180°=540°.设这个多边形的边数为n,则(n-2)×180°=540°,解得n=5,即这个多边形是五边形,故答案为五.
9.【解】(1)设多边形的边数为n,则 180°×(n-2)=1470°,解得
∵n为正整数,∴ 多边形的内角和不可能为1470°.
(2)由题意可知,该多边形的边数为10,∴该多边形的内角和为180°×(10-2)=1440°.
(3)1 440°÷10-360°÷10=144°-36°=108°.
答:该正多边形的一个内角比一个外角大108°.
刷提升
1. C 【解析】由题意得,机器人行走的路径是一个正多边形,∴该机器人从开始到结束共行走的路程为 故选 C
2. A 【解析】如图,连接GC并延长交BD 于点H,连接AE.∵六边形ABCDEF 是正六边形,∴AB=BC=CD=DE=EF=AF,∠F = ∠FAB = ∠ABC =∠BCD =∠CDE=∠DEF=120°.∵△BDG是等边三角形,∴BG=DG=BD.又∵CG=CG,∴△BCG≌△DCG(SSS),∴∠BGC=∠DGC=30°.∵ 易得∠GBC = ∠DBC = 30°,∴ △GBC ≌△DBC 3.设CH=x,则 即 五边形ABDEF的面积为3+12=15.故选A.
3.5 【解析】如图,过 作 则∠4= ∵∠1 - ∠2 = 36°, 设正多边形的一个内角为x,则∠4=180°-x,∴x=36°+∠3,∴∠3=x-36°,∴180°-x=x-36°,解得x=108°,∴ ∠4= 这个正多边形的边数为360°÷ 72°=5,故答案为5.
4.(1)12 (2)72 【解析】(1)∵正六边形的一个内角为 正五边形的一个内角为 ∴∠CDH=∠CDE-∠HDE=120°-108°=12°,故答案为12.(2)由(1)得∠CDH=12°,同理可证∠FEM=12°.∵∠M=108°,MG=ME, ∴ ∠FEN=∠FEM+∠MEG=12°+36°=48°.在四边形ANEF 中,∠A+∠F+∠FEN+∠ANE=360°,∴∠ANE=360°-120°-120°-48°=72°,故答案为72.
5.6 【解析】∵正五边形的外角和为360°,∴正五边形每个外角的度数为360°÷ 5=72°,∴正五边形每个内角为180°-72°=108°,∴拼接一圈后,中间正多边形的每个内角为360°-2× 解得n=6.故答案为6.
刷素养·
6.【解】(1)由折叠可得,∠EA'D=∠A.∵∠1=∠A+∠EA'D,∴ ∠1=2∠A.故答案为∠1=2∠A.
(2)2∠A=∠1+∠2.理由如下:
∵∠1+∠A'DA+∠2+∠A'EA=360°,∠A+ ∠1+∠2.由折叠可得∠A=∠A',∴2∠A=∠1+∠2.
(3)如图,由折叠可得∠A=∠A'.∵ ∠1=∠DFA+∠A,∠DFA=∠A'+∠2,∴ ∠1=∠A+∠A'+∠2=2∠A+∠2,∴2∠A=∠1-∠2=56°,∴∠A=28°.故答案为28°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
