10.1.2 两角和与差的正弦 练习(2课时,含详解)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 10.1.2 两角和与差的正弦 练习(2课时,含详解)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 51.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 17:44:56 | ||
图片预览



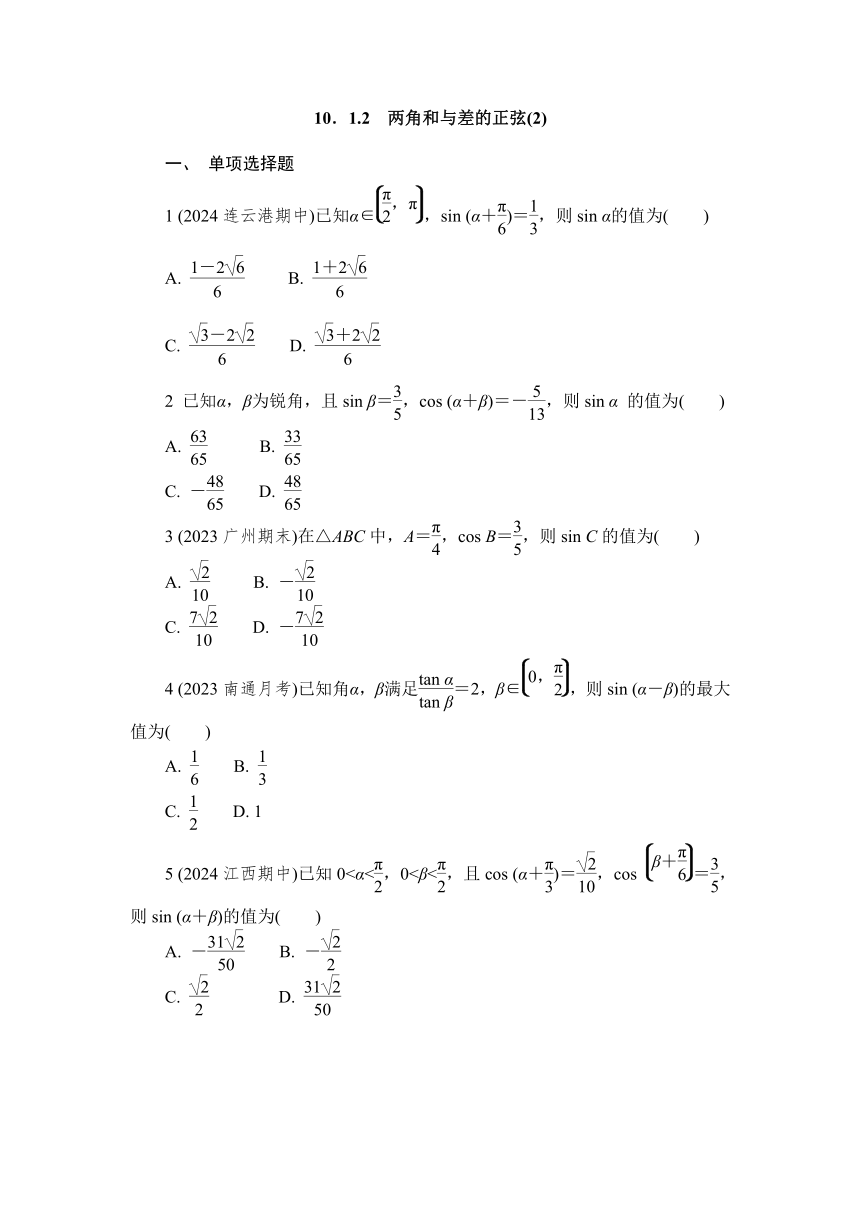

文档简介
10.1.2 两角和与差的正弦(1)
一、 单项选择题
1 sin cos -cos sin 的值是( )
A. - B. C. -1 D. 1
2 (2024莆田期中)已知α∈,sin α=,则sin (α+)的值是( )
A. B.
C. D.
3 已知sin (α-β)cos α-cos (α-β)sin α=,且β为第三象限角,则tan β的值为( )
A. B. C. D.
4 (2023烟台期中)已知cos (α+)=,0<α<π,则sin α的值为( )
A. B.
C. D.
5 (2024连云港期中)已知sin α+cos β=,cos α+sin β=-,则sin (α+β)的值为( )
A. B. -
C. - D. -
6 (2024南开期中)在△ABC中,已知sin C=2sin (B+C)cos B,则△ABC一定是( )
A. 等腰直角三角形 B. 等腰三角形
C. 直角三角形 D. 等边三角形
二、 多项选择题
7 下列对等式sin (α+β)=sin α+sin β的描述中,正确的是( )
A. 对任意的角α,β都成立
B. 当α=β=0时成立
C. 只对有限个α,β的值成立
D. 有无限个α,β的值使等式成立
8 (2024河北开学考试)已知α,β∈,cos (α+β)=,sin (α-β)=,则下列结论中正确的是( )
A. sin (α+β)=
B. cos (α-β)=-
C. sin 2α=
D. =
三、 填空题
9 (2024成都期中)已知α,β∈,sin α=,cos β=,则sin (α-β)=________.
10 (2023潍坊期末)已知cos θ+cos (θ+)=,θ∈,则sin θ=________.
11 (2023镇江中学期中)已知a>0,函数f(x)=sin (x-)-a sin x的最大值为,则a=________.
四、 解答题
12 已知sin =-,sin =,且α∈,β∈,求sin (α-β)的值.
13 (2024江苏月考)已知α,β∈,且cos α=,sin (α-β)=.
(1) 求sin (2α-β)的值;
(2) 求β的值.
10.1.2 两角和与差的正弦(2)
一、 单项选择题
1 (2024连云港期中)已知α∈,sin (α+)=,则sin α的值为( )
A. B.
C. D.
2 已知α,β为锐角,且sin β=,cos (α+β)=-,则sin α 的值为( )
A. B.
C. - D.
3 (2023广州期末)在△ABC中,A=,cos B=,则sin C的值为( )
A. B. -
C. D. -
4 (2023南通月考)已知角α,β满足=2,β∈,则sin (α-β)的最大值为( )
A. B.
C. D. 1
5 (2024江西期中)已知0<α<,0<β<,且cos (α+)=,cos =,则sin (α+β)的值为( )
A. - B. -
C. D.
6 (2023淄博实验中学月考)已知α,β∈(0,π),sin (α-β)=,=-,则 α+β的值为( )
A. B.
C. D. 或
二、 多项选择题
7 已知在△ABC中,sin A+cos A=m,则下列说法中正确的是( )
A. m的取值范围是[-,]
B. 若0C. 若m=,则tan A=-
D. 若m=1,则△ABC为直角三角形
8 (2024安徽月考)下列结论中,正确的有( )
A. 若A,B为锐角三角形的两内角,则sin A>cos B
B. sin 735°cos 45°+sin 105°sin 135°=
C. α,β∈R,sin2α-sin2β=sin(α+β)sin (α-β)
D. α,β∈R,cos2α-cos2β=cos(α+β)sin (α-β)
三、 填空题
9 (2023湖南月考)已知α为锐角,且sin α+cos α=,则tan α=________.
10 已知sin =-,则cos x+cos =________.
11 (2023镇江期中)已知tan β=2tan (α+β),则=________.
四、 解答题
12 (2023上海南汇中学期中)三角函数内容丰富,公式很多. 若仔细观察、大胆猜想、科学求证,你也能发现其中的一些奥秘. 现有如下两个等式:
①+=;
②+=.
根据以上等式,请你猜想出一个一般性的结论并证明.
13 (2024重庆期中)已知向量a=(cos α,sin α),b=(cos β,sin β),|a-b|=.
(1) 求cos (α-β)的值;
(2) 若-<β<0<α<π,sin β=-,求sin α的值.
10.1.2 两角和与差的正弦(1)
1. B 原式=sin cos +cos sin =sin (+)=sin =.
2. B 因为α∈,sin α=,所以cos α=,所以sin =sin αcos +cos αsin =×+×=.
3. C 由sin (α-β)cos α-cos (α-β)sin α=,得sin [(α-β)-α]=sin (-β)=-sin β=,即sin β=-.又β是第三象限角,则cos β=-,所以tan β===.
4. C 因为0<α<π,所以<α+<.又cos (α+)=>0,所以<α+<,所以sin ==,所以sinα=sin [(α+)-]=sin (α+)cos -cos (α+)sin =×-×=.
5. C 由sin α+cos β=,得(sin α+cos β)2=sin2α+2sinαcos β+cos2β=.由cosα+sin β=-,得(cos α+sin β)2=cos2α+2cosαsin β+sin2β=,将两式相加可得2sinαcos β+2cos αsin β=-2=-,即sin αcos β+cos αsin β=-,即sin (α+β)=sin αcos β+cos αsin β=-.
6. B 因为sin C=2sin (B+C)cos B,即sin (A+B)=2sin A cos B,所以sin A cos B+cos A sin B=2sin A cos B,所以sin A cos B-cos A sin B=0,即sin (A-B)=0,所以A-B=0或A-B=π(舍去),即A=B,所以△ABC一定是等腰三角形.
7. BD 因为sin (α+β)=sin αcos β+cos αsin β=sin α+sin β,所以当cos β=1且cos α=1时,可使等式成立,所以α=2k1π(k1∈Z),β=2k2π(k2∈Z).因为k1,k2∈Z,所以α,β有无限多个,包含α=β=0.故选BD.
8. ACD 对于A,由α,β∈,得α+β∈(0,π),所以sin (α+β)==,故A正确;对于B,由α,β∈,得α-β∈,所以cos(α-β)==,故B错误;对于C,因为2α=(α+β)+(α-β),所以sin2α=sin [(α+β)+(α-β)]=sin (α+β)cos (α-β)+cos (α+β)sin (α-β)=×+×=,故C正确;对于D,因为===,所以=,解得=,故D正确.故选ACD.
9. 因为α,β∈,sin α=,cos β=,所以cos α==,sin β==,所以sin (α-β)=sin αcos β-cos αsin β=×-×=.
10. 因为cos θ+cos =,所以cos θ+cos θcos -sin θsin =,即cos θ-sin θ=,所以=,即cos =.因为θ∈,所以θ+∈,则sin ==,所以sinθ=sin [(θ+)-]=sin (θ+)cos -cos sin =×-×=.
11. 2 由a>0,f(x)=sin -a sin x=sin x-cos x,且f(x)的最大值为,得+=3,解得a=2或a=-1(舍去).
12. 因为α∈,所以-α∈,
所以cos =.
又β∈,所以+β∈,
所以cos =-,
所以sin (α-β)=sin (π-α+β)=sin [(-α)+(+β)]=sin cos +cos (-α)sin (+β)=×+×=.
13. (1) 由α,β∈,得α-β∈.
又sin (α-β)=,
则cos (α-β)==.
又cos α=,所以sin α==,
所以sin (2α-β)=sin [(α-β)+α]=sin (α-β)cos α+cos (α-β)sin α=×+×=.
(2) sin β=sin [α-(α-β)]=sin αcos (α-β)-cos αsin (α-β)=×-×=,
又β∈,故β=.
10.1.2 两角和与差的正弦(2)
1. D 因为α∈,所以α+∈.又因为sin =>0,所以α+∈,所以cos =-,则sin α=sin =sin cos -cos sin =×-×=.
2. A 因为α,β为锐角,所以α+β∈(0,π).因为cos (α+β)=-,所以sin (α+β)=.因为sin β=,所以cos β==,故sinα=sin [(α+β)-β]=sin (α+β)cos β-cos (α+β)sin β=×+×=.
3. C 因为cos B=,B∈(0,π),所以sin B==.又A=,则sinC=sin [π-(A+B)]=sin (A+B)=sin A cos B+cos A sin B=×+×=.
4. B 因为=2,所以sin αcos β=2sin βcos α.设sin (α+β)=x=sin αcos β+sin βcos α,则sin βcos α=,sin αcos β=,所以sin (α-β)=sin αcos β-sin βcos α=.又sin (α+β)=x,所以x的最大值为1,故sin (α-β)的最大值为.
5. C 因为0<α<,所以<α+<.又cos (α+)=,所以sin =.因为0<β<,所以<β+<.因为cos (β+)=,所以sin (β+)=,则sin (α+β)=-cos [(α+)+(β+)]=sin (α+)sin (β+)-cos (α+)cos =×-×=.
6. B 因为α,β∈(0,π),=-<0,所以0<α<,<β<π或0<β<,<α<π.若0<α<,<β<π,则-π<α-β<0,此时sin (α-β)<0(舍去);若0<β<,<α<π,则0<α-β<π,此时sin (α-β)>0(符合题意),所以0<β<,<α<π,则α+β∈.因为sin (α-β)=且=-,所以sin αcos β-cos αsin β=且=-,解得sin αcos β=,cos αsin β=-,则sin (α+β)=sin αcos β+cos αsin β=-.又α+β∈,所以α+β=.
7. BCD m=sin A+cos A=sin (A+).对于A,因为A为三角形的内角,所以A∈(0,π),所以A+∈,所以sin (A+)∈,则m∈(-1,],故A不正确;对于B,若00.又(sin A-cos A)2=1-2sin A cos A=,所以sin A-cos A=②.由①②解得sin A=,cos A=-,所以tan A==-,故C正确;对于D,当 m=1时,sin A+cos A=1,所以(sin A+cos A)2=1+2sin A cos A=1,所以sin A cos A=0.在△ABC中,sin A≠0,所以cos A=0,A=90°,即△ABC为直角三角形,故D正确.故选BCD.
8. AC 对于A,由题意可得则0<-B9. 因为sin α+cos α=,所以sin α+cos α=,即sin =.因为α为锐角,所以<α+<,所以α+=,即α=,所以tan α=.
10. -1 因为sin =-,所以cos x+cos (x-)=cos x+sin x=(cos x+sin x)=sin (x+)=-1.
11. -3 因为tan β=2tan (α+β),所以=====-3.
12. 猜想:+=,证明如下:
由诱导公式可得cos (90°-α)=sin α,
sin (135°-α)=sin (45°+α),
所以+===.
13. (1) 由题意,得|a|=1,|b|=1.
由|a-b|=,
得a2-2a·b+b2=,
所以a·b=cos αcos β+sin αsin β=cos (α-β)=.
(2) 因为-<β<0<α<π,
所以0<α-β<.
又cos (α-β)=,所以0<α-β<,
所以sin (α-β)==.
因为-<β<0,sinβ=-,
所以cos β==,
故sinα=sin [(α-β)+β]=sin (α-β)cos β+cos (α-β)sin β=×+×=.
一、 单项选择题
1 sin cos -cos sin 的值是( )
A. - B. C. -1 D. 1
2 (2024莆田期中)已知α∈,sin α=,则sin (α+)的值是( )
A. B.
C. D.
3 已知sin (α-β)cos α-cos (α-β)sin α=,且β为第三象限角,则tan β的值为( )
A. B. C. D.
4 (2023烟台期中)已知cos (α+)=,0<α<π,则sin α的值为( )
A. B.
C. D.
5 (2024连云港期中)已知sin α+cos β=,cos α+sin β=-,则sin (α+β)的值为( )
A. B. -
C. - D. -
6 (2024南开期中)在△ABC中,已知sin C=2sin (B+C)cos B,则△ABC一定是( )
A. 等腰直角三角形 B. 等腰三角形
C. 直角三角形 D. 等边三角形
二、 多项选择题
7 下列对等式sin (α+β)=sin α+sin β的描述中,正确的是( )
A. 对任意的角α,β都成立
B. 当α=β=0时成立
C. 只对有限个α,β的值成立
D. 有无限个α,β的值使等式成立
8 (2024河北开学考试)已知α,β∈,cos (α+β)=,sin (α-β)=,则下列结论中正确的是( )
A. sin (α+β)=
B. cos (α-β)=-
C. sin 2α=
D. =
三、 填空题
9 (2024成都期中)已知α,β∈,sin α=,cos β=,则sin (α-β)=________.
10 (2023潍坊期末)已知cos θ+cos (θ+)=,θ∈,则sin θ=________.
11 (2023镇江中学期中)已知a>0,函数f(x)=sin (x-)-a sin x的最大值为,则a=________.
四、 解答题
12 已知sin =-,sin =,且α∈,β∈,求sin (α-β)的值.
13 (2024江苏月考)已知α,β∈,且cos α=,sin (α-β)=.
(1) 求sin (2α-β)的值;
(2) 求β的值.
10.1.2 两角和与差的正弦(2)
一、 单项选择题
1 (2024连云港期中)已知α∈,sin (α+)=,则sin α的值为( )
A. B.
C. D.
2 已知α,β为锐角,且sin β=,cos (α+β)=-,则sin α 的值为( )
A. B.
C. - D.
3 (2023广州期末)在△ABC中,A=,cos B=,则sin C的值为( )
A. B. -
C. D. -
4 (2023南通月考)已知角α,β满足=2,β∈,则sin (α-β)的最大值为( )
A. B.
C. D. 1
5 (2024江西期中)已知0<α<,0<β<,且cos (α+)=,cos =,则sin (α+β)的值为( )
A. - B. -
C. D.
6 (2023淄博实验中学月考)已知α,β∈(0,π),sin (α-β)=,=-,则 α+β的值为( )
A. B.
C. D. 或
二、 多项选择题
7 已知在△ABC中,sin A+cos A=m,则下列说法中正确的是( )
A. m的取值范围是[-,]
B. 若0
D. 若m=1,则△ABC为直角三角形
8 (2024安徽月考)下列结论中,正确的有( )
A. 若A,B为锐角三角形的两内角,则sin A>cos B
B. sin 735°cos 45°+sin 105°sin 135°=
C. α,β∈R,sin2α-sin2β=sin(α+β)sin (α-β)
D. α,β∈R,cos2α-cos2β=cos(α+β)sin (α-β)
三、 填空题
9 (2023湖南月考)已知α为锐角,且sin α+cos α=,则tan α=________.
10 已知sin =-,则cos x+cos =________.
11 (2023镇江期中)已知tan β=2tan (α+β),则=________.
四、 解答题
12 (2023上海南汇中学期中)三角函数内容丰富,公式很多. 若仔细观察、大胆猜想、科学求证,你也能发现其中的一些奥秘. 现有如下两个等式:
①+=;
②+=.
根据以上等式,请你猜想出一个一般性的结论并证明.
13 (2024重庆期中)已知向量a=(cos α,sin α),b=(cos β,sin β),|a-b|=.
(1) 求cos (α-β)的值;
(2) 若-<β<0<α<π,sin β=-,求sin α的值.
10.1.2 两角和与差的正弦(1)
1. B 原式=sin cos +cos sin =sin (+)=sin =.
2. B 因为α∈,sin α=,所以cos α=,所以sin =sin αcos +cos αsin =×+×=.
3. C 由sin (α-β)cos α-cos (α-β)sin α=,得sin [(α-β)-α]=sin (-β)=-sin β=,即sin β=-.又β是第三象限角,则cos β=-,所以tan β===.
4. C 因为0<α<π,所以<α+<.又cos (α+)=>0,所以<α+<,所以sin ==,所以sinα=sin [(α+)-]=sin (α+)cos -cos (α+)sin =×-×=.
5. C 由sin α+cos β=,得(sin α+cos β)2=sin2α+2sinαcos β+cos2β=.由cosα+sin β=-,得(cos α+sin β)2=cos2α+2cosαsin β+sin2β=,将两式相加可得2sinαcos β+2cos αsin β=-2=-,即sin αcos β+cos αsin β=-,即sin (α+β)=sin αcos β+cos αsin β=-.
6. B 因为sin C=2sin (B+C)cos B,即sin (A+B)=2sin A cos B,所以sin A cos B+cos A sin B=2sin A cos B,所以sin A cos B-cos A sin B=0,即sin (A-B)=0,所以A-B=0或A-B=π(舍去),即A=B,所以△ABC一定是等腰三角形.
7. BD 因为sin (α+β)=sin αcos β+cos αsin β=sin α+sin β,所以当cos β=1且cos α=1时,可使等式成立,所以α=2k1π(k1∈Z),β=2k2π(k2∈Z).因为k1,k2∈Z,所以α,β有无限多个,包含α=β=0.故选BD.
8. ACD 对于A,由α,β∈,得α+β∈(0,π),所以sin (α+β)==,故A正确;对于B,由α,β∈,得α-β∈,所以cos(α-β)==,故B错误;对于C,因为2α=(α+β)+(α-β),所以sin2α=sin [(α+β)+(α-β)]=sin (α+β)cos (α-β)+cos (α+β)sin (α-β)=×+×=,故C正确;对于D,因为===,所以=,解得=,故D正确.故选ACD.
9. 因为α,β∈,sin α=,cos β=,所以cos α==,sin β==,所以sin (α-β)=sin αcos β-cos αsin β=×-×=.
10. 因为cos θ+cos =,所以cos θ+cos θcos -sin θsin =,即cos θ-sin θ=,所以=,即cos =.因为θ∈,所以θ+∈,则sin ==,所以sinθ=sin [(θ+)-]=sin (θ+)cos -cos sin =×-×=.
11. 2 由a>0,f(x)=sin -a sin x=sin x-cos x,且f(x)的最大值为,得+=3,解得a=2或a=-1(舍去).
12. 因为α∈,所以-α∈,
所以cos =.
又β∈,所以+β∈,
所以cos =-,
所以sin (α-β)=sin (π-α+β)=sin [(-α)+(+β)]=sin cos +cos (-α)sin (+β)=×+×=.
13. (1) 由α,β∈,得α-β∈.
又sin (α-β)=,
则cos (α-β)==.
又cos α=,所以sin α==,
所以sin (2α-β)=sin [(α-β)+α]=sin (α-β)cos α+cos (α-β)sin α=×+×=.
(2) sin β=sin [α-(α-β)]=sin αcos (α-β)-cos αsin (α-β)=×-×=,
又β∈,故β=.
10.1.2 两角和与差的正弦(2)
1. D 因为α∈,所以α+∈.又因为sin =>0,所以α+∈,所以cos =-,则sin α=sin =sin cos -cos sin =×-×=.
2. A 因为α,β为锐角,所以α+β∈(0,π).因为cos (α+β)=-,所以sin (α+β)=.因为sin β=,所以cos β==,故sinα=sin [(α+β)-β]=sin (α+β)cos β-cos (α+β)sin β=×+×=.
3. C 因为cos B=,B∈(0,π),所以sin B==.又A=,则sinC=sin [π-(A+B)]=sin (A+B)=sin A cos B+cos A sin B=×+×=.
4. B 因为=2,所以sin αcos β=2sin βcos α.设sin (α+β)=x=sin αcos β+sin βcos α,则sin βcos α=,sin αcos β=,所以sin (α-β)=sin αcos β-sin βcos α=.又sin (α+β)=x,所以x的最大值为1,故sin (α-β)的最大值为.
5. C 因为0<α<,所以<α+<.又cos (α+)=,所以sin =.因为0<β<,所以<β+<.因为cos (β+)=,所以sin (β+)=,则sin (α+β)=-cos [(α+)+(β+)]=sin (α+)sin (β+)-cos (α+)cos =×-×=.
6. B 因为α,β∈(0,π),=-<0,所以0<α<,<β<π或0<β<,<α<π.若0<α<,<β<π,则-π<α-β<0,此时sin (α-β)<0(舍去);若0<β<,<α<π,则0<α-β<π,此时sin (α-β)>0(符合题意),所以0<β<,<α<π,则α+β∈.因为sin (α-β)=且=-,所以sin αcos β-cos αsin β=且=-,解得sin αcos β=,cos αsin β=-,则sin (α+β)=sin αcos β+cos αsin β=-.又α+β∈,所以α+β=.
7. BCD m=sin A+cos A=sin (A+).对于A,因为A为三角形的内角,所以A∈(0,π),所以A+∈,所以sin (A+)∈,则m∈(-1,],故A不正确;对于B,若0
8. AC 对于A,由题意可得则0<-B
10. -1 因为sin =-,所以cos x+cos (x-)=cos x+sin x=(cos x+sin x)=sin (x+)=-1.
11. -3 因为tan β=2tan (α+β),所以=====-3.
12. 猜想:+=,证明如下:
由诱导公式可得cos (90°-α)=sin α,
sin (135°-α)=sin (45°+α),
所以+===.
13. (1) 由题意,得|a|=1,|b|=1.
由|a-b|=,
得a2-2a·b+b2=,
所以a·b=cos αcos β+sin αsin β=cos (α-β)=.
(2) 因为-<β<0<α<π,
所以0<α-β<.
又cos (α-β)=,所以0<α-β<,
所以sin (α-β)==.
因为-<β<0,sinβ=-,
所以cos β==,
故sinα=sin [(α-β)+β]=sin (α-β)cos β+cos (α-β)sin β=×+×=.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
