6.3相似图形(含解析)苏科版九年级数学下册
文档属性
| 名称 | 6.3相似图形(含解析)苏科版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 539.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 12:04:07 | ||
图片预览


文档简介
6.3相似图形
一、单选题
1.下列图中,大小图形非相似图形的是( )
A. B. C. D.
2.下列说法正确的是( )
A.矩形都是相似图形
B.等边三角形都是相似三角形
C.各边对应成比例的多边形是相似多边形
D.边长相等的菱形都相似
3.下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
4.下面两个图形一定相似的是( )
A.两个等腰三角形 B.两个等腰直角三角形
C.两个菱形 D.两个矩形
二、填空题
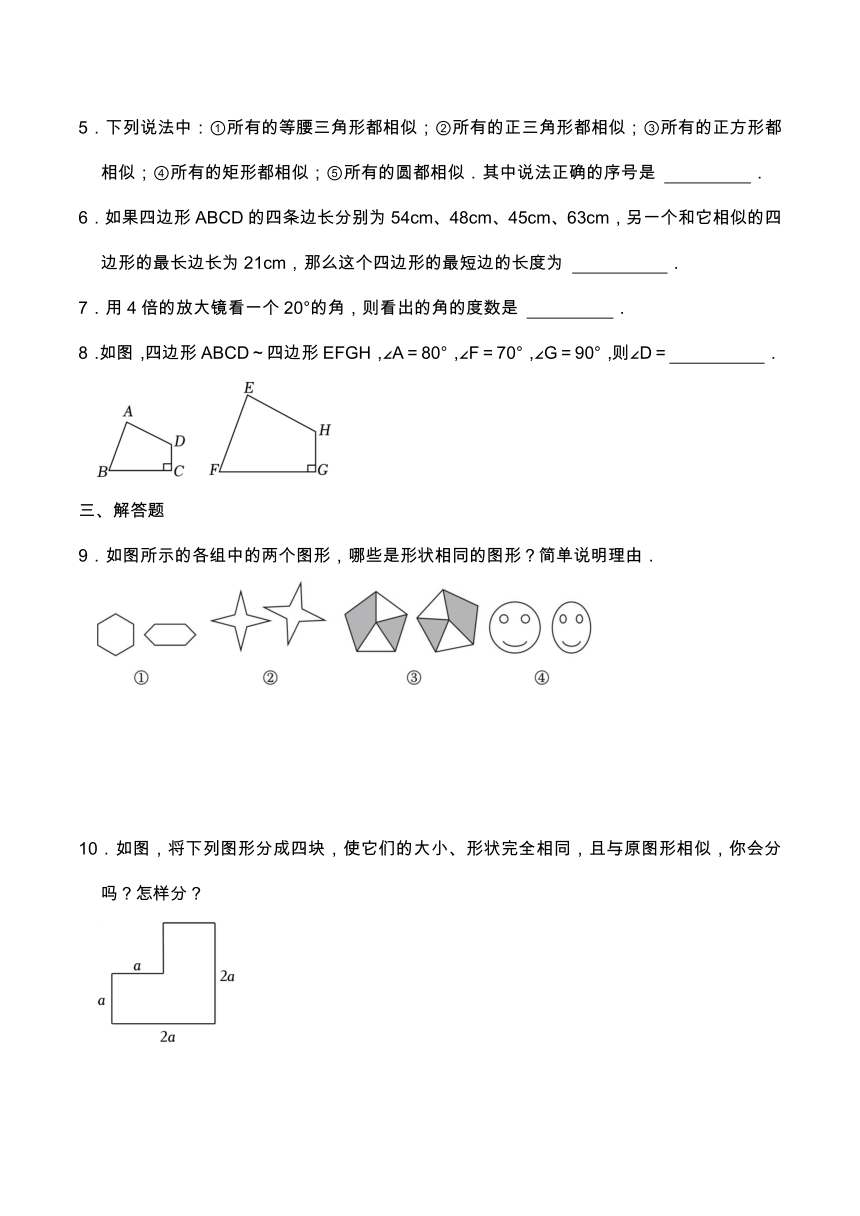
5.下列说法中:①所有的等腰三角形都相似;②所有的正三角形都相似;③所有的正方形都相似;④所有的矩形都相似;⑤所有的圆都相似.其中说法正确的序号是 .
6.如果四边形ABCD的四条边长分别为54cm、48cm、45cm、63cm,另一个和它相似的四边形的最长边长为21cm,那么这个四边形的最短边的长度为 .
7.用4倍的放大镜看一个20°的角,则看出的角的度数是 .
8.如图,四边形ABCD~四边形EFGH,∠A=80°,∠F=70°,∠G=90°,则∠D= .
三、解答题
9.如图所示的各组中的两个图形,哪些是形状相同的图形?简单说明理由.
10.如图,将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?
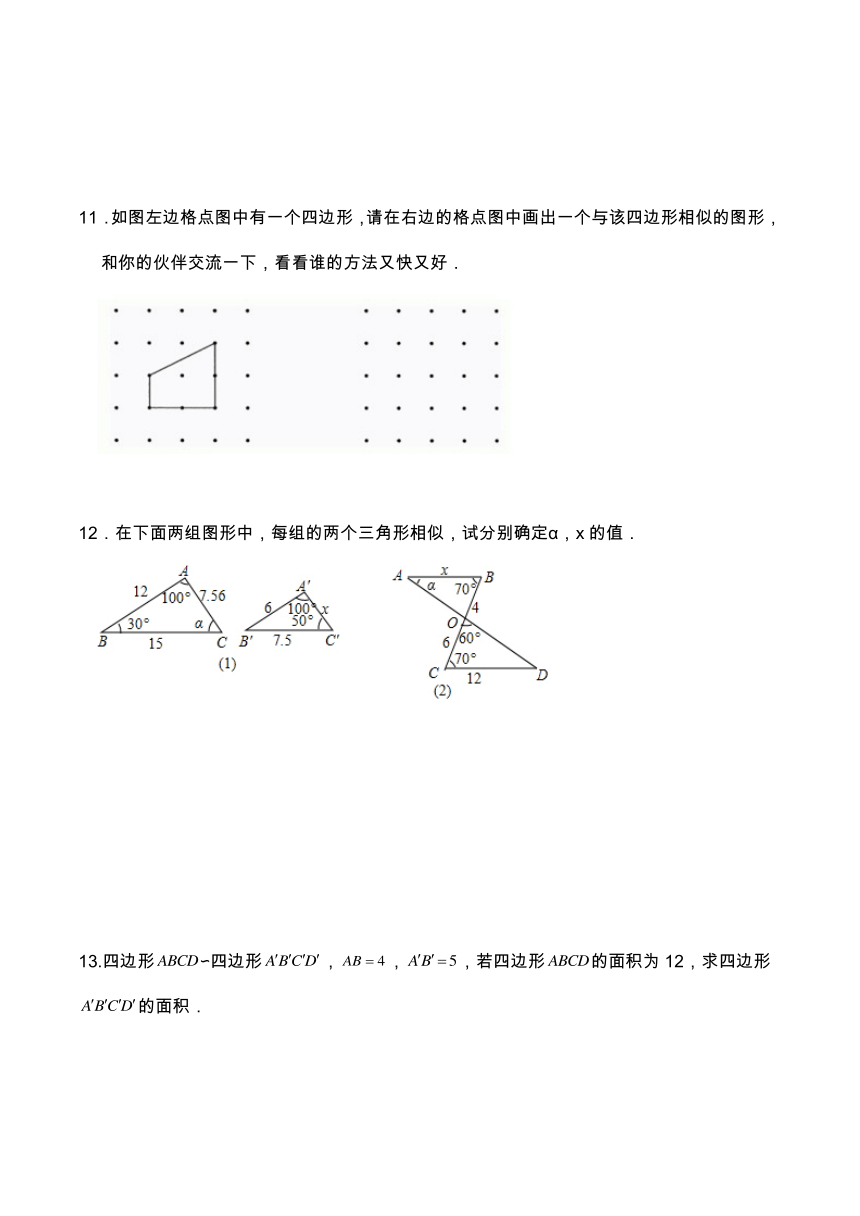
11.如图左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形,和你的伙伴交流一下,看看谁的方法又快又好.
12.在下面两组图形中,每组的两个三角形相似,试分别确定α,x的值.
13.四边形∽四边形,,,若四边形的面积为12,求四边形的面积.
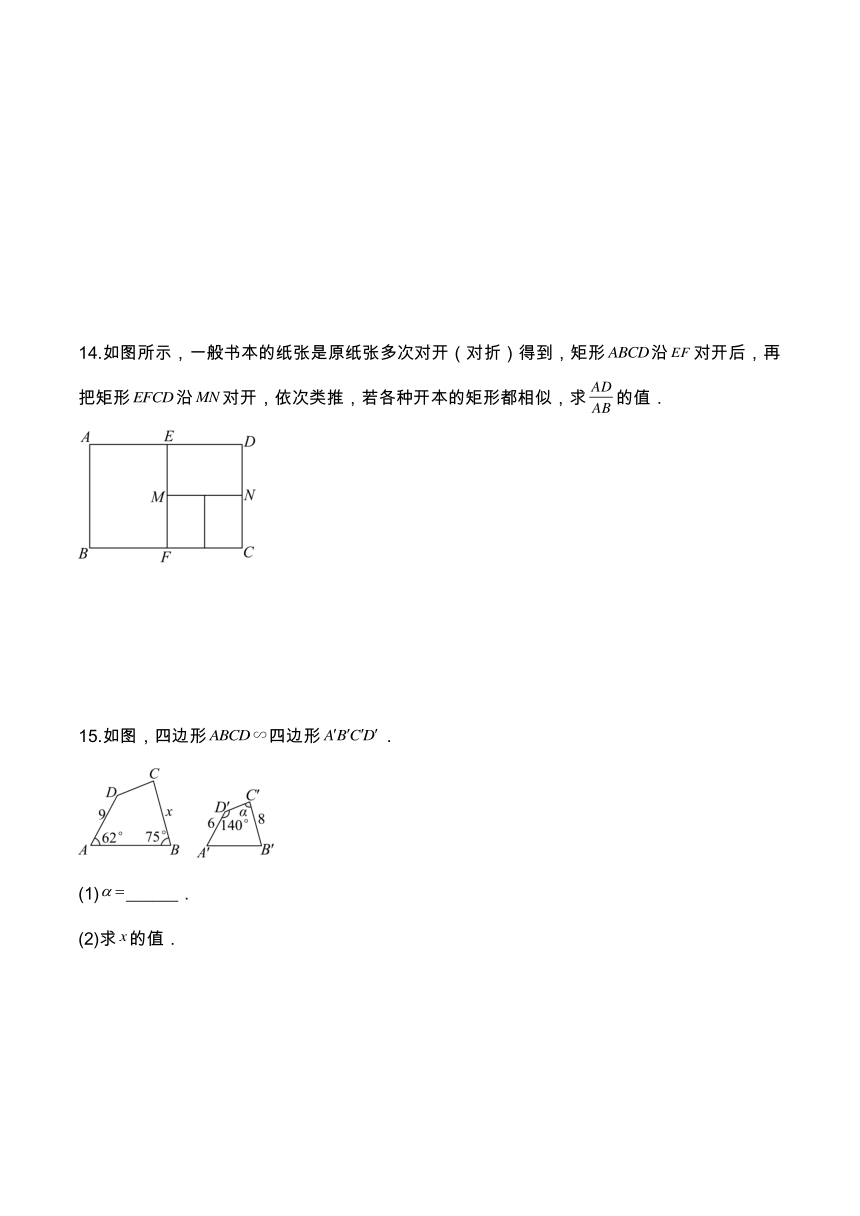
14.如图所示,一般书本的纸张是原纸张多次对开(对折)得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,求的值.
15.如图,四边形四边形.
(1)______.
(2)求的值.
16.如图在矩形中,,,、分别是、上的点,且,两动点、都以2cm/s的速度分别从、两点沿、向、两点运动,判断当、运动多长时间能使矩形与矩形相似,并证明你的结论.
17.将下列图形分别分成四小块,使它们得的形状大小完全相同,并且与原图形相似,应怎样分?(画出大致图形即可)
(1)
(2)
18.形状相同(即长与宽之比相等)的矩形是相似矩形,已知一个矩形长为,宽为1.
一分为二
(1)如图1,将矩形分割为一个正方形(阴影部分)和小矩形,小矩形恰与原矩形相似,则的值为______.
(2)如图2,将矩形分割为两个矩形,使每个小矩形均与原矩形相似,则的值为______.
一分为多
(3)有同学说“无论为何值,该矩形总可以分割为几个小矩形,这几个小矩形都与原矩形相似”,你同意这个说法吗?若同意,在图3中画出一种可行的分割方案;若不同意,举出反例.
一分为三
(4)将矩形分割为三个矩形,使每个小矩形均与原矩形相似.画出所有可能的分割方案的示意图,并在每个示意图下方直接写出对应的的值.
19.如图:矩形ABCD的长AB=30,宽BC=20.
(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;
(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?
20.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).
(1)当n=5时,共向外作出了 个小等边三角形,每个小等边三角形的面积为 ;
(2)当n=k时,共向外作出了 个小等边三角形,这些小等边三角形的面积和为 (用含k的式子表示).
21.如果四边形的一条对角线把这个四边形分成两个三角形并且相似(不全等),我们就把这条对角线称为“完美对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时,求证:对角线BD是四边形ABCD的“完美对角线.
(2)如图2,在四边形ABCD中,AC平分∠BCD,当∠BAD与∠BCD满足什么关系时,对角线AC是四边形ABCD的“完美对角线”?请说明理由.
参考答案
一、单选题
1.
【分析】根据相似图形的定义可知.
【解答】解:观察图形可知,A、B、C中的两个图形都是相似图形,D中的两个图形不是相似图形.
故选:D.
2.
【分析】各边对应成比例,各角对应相等的多边形是相似多边形,由此即可判断.
【解答】解:A、矩形的长和宽不一定对应成比例,矩形不一定都相似,故A不符合题意;
B、等边三角形的三边对应成比例,等边三角形都是相似三角形,故B符合题意;
C、多边形各边对应成比例,但多边形的各角不一定对应相等,各边对应成比例的多边形不一定是相似多边形,故C不符合题意;
D、菱形的各角不一定对应相等,边长相等的菱形不一定都相似,故D不符合题意.
故选:B.
3.
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
【解答】解:观察可得:甲和丁对应角相等,对应边成比例,且形状相同,大小不同,
故选:D.
4.
【分析】根据相似三角形的判定依据等腰直角三角形的性质判断即可.
【解答】解:两个等腰直角三角形一定相似,
故选:B.
二、填空题
5.
【分析】直接利用相似图形的定义得出答案.
【解答】解:①所有的等腰三角形都相似,错误,对应边不一定成比例,对应角不一定相等;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误,对应边不一定成比例;
⑤所有的圆都相似,正确.
故答案为:②③⑤.
6.
【分析】设这个四边形的最短边的长度为x cm,然后根据相似多边形的性质可得,从而进行计算即可解答.
【解答】解:设这个四边形的最短边的长度为x cm,
由题意得:
,
解得:x=15,
∴这个四边形的最短边的长度为15cm,
故答案为:15cm.
7.
【分析】角的大小是指两边张开的大小,与两条边的张开程度有关,用放大4倍的放大镜看一个20°的角,也就是把边变长了,而两边张开的大小没变,即角的度数没变,
【解答】解:用一个放大4倍的放大镜看一个20度的角,看到的这个角仍是20度;
故答案为:20°.
8.
【分析】根据相似多边形的对应角相等求解即可.
【解答】解:∵四边形ABCD~四边形EFGH,
∴∠F=∠B=70°,∠G=∠C=90°,
∵∠A=80°,
∴∠D=360°﹣∠A﹣∠B﹣∠C=120°,
故答案为:120°.
三、解答题
9.解:②和③中的两个图形经过放大或缩小得到另一个图形,所以它们的形状相同.
10.解:作图如下:
11.解:本题答案不唯一
12.解:图1中,在△ABC中,∠C=180°﹣∠A﹣∠B=50°,
∴α=50°,
∵△ABC∽△A′B′C′,
∴,
∴,
∴A′C′=3.78,
∴x=AC=3.78.
图2中,∵∠AOB=∠COD=60°,
∴∠A=180°﹣∠B﹣∠AOB=50°,
∴α=50°,
∵△ABO∽DCO,
∴,
∴,
∴AB=8,
∴x=8.
13.解:∵四边形∽四边形,,,
∴四边形与四边形的相似比为,
∴,即,
∴.
14.设,,则,,
由相似图形的性质得:,即,
解得或(不符题意,舍去),
则.
15.(1)解:∵四边形四边形,
∴,,
∵,
∴,
故答案为:;
(2)解:∵四边形四边形,
∴,即,
解得.
16.解:设运动时间能使矩形与矩形相似,
由题意或,
解得:或.
当时,,
∵,
又∵与都是矩形,
∴矩形与矩形相似.
同理可证当时矩形与矩形相似.
17.(1)解:作图如下:
(2)解:作图如下:
18.解:(1)由图可知阴影正方形的边长为1,
∴小长方形的宽为,长为1,
∵小矩形与原矩形相似,
∴,
∴,
解得:或(边长不能为负舍去),
∴;
(2)∵两小矩形的长都为1,且与原矩形的长宽比相同,
∴,
∴,
解得:或(舍去),
∴;
(3)同意,如下图连接矩形的四条边的中点,将矩形分为4个小矩形,
四个小矩形的长和宽都为和,长宽比为与原矩形长宽比相同;
(4)共有四种情况:
①如下图沿原矩形的长3等分,
小矩形和原矩形的长宽比都为a,
小矩形的长为1,则宽为,
∴,
∴,
解得:或(舍去),
∴;
②如下图先将矩形分割为两个小矩形,再将右边矩形两等分使宽都为,
根据原矩形的长宽比可得:
左边矩形的宽为,右边矩形的长为,
∴,
∴,
解得:或(舍去),
∴;
③如下图先将矩形分割为两个小矩形,再将右边矩形两等分使长都为,
根据原矩形的长宽比可得:
左边矩形的宽为,右边矩形的宽为,
∴∴,
∴,
解得:或(舍去),
∴;
④如下图先将矩形分割为两个小矩形,再将右边矩形分割为两个小矩形使两个矩形的长与宽的和为1,
根据原矩形的长宽比可得:
左边矩形的宽为,
∴右边两矩形的宽和长为,
∴右上矩形的长为,右下矩形的宽为,
∴,
∴,
设,则,
∴,
解得:或(舍去),
∴,
∴;
19.解:(1)不相似,理由如下:
AB=30,A′B′=28,BC=20,B′C′=18,
而,
∴图中两个矩形不相似;
(2)矩形ABCD与A′B′C′D′相似,则,
则:,
解得x=1.5,
或,
解得x=9.
综上所述,x=1.5或9时,图中的两个矩形相似.
20.解:(1)当n=5时,共有3×(5﹣2)=9个小等边三角形,
∴每个小三角形与大三角形边长的比,
∵大三角形的面积是S,
∴每个小三角形的面积为;‘
(2)由(1)可知,当n=k时,共有3×(k﹣2)=3(k﹣2),每个小三角形的面积为.
21.(1)证明:如图1中,
∵AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC∠ABC=35°,
∵∠ADC+∠C=180°,∠ADC=145°,
∴∠C=35°,
∴∠ADB=∠ABD=∠DBC=∠C=35°,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“完美对角线”.
(2)解:如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“完美对角线”.
理由:∵AC平分∠BCD,
∴∠ACB=∠ACD,
∵∠B+∠ACB+∠BAC=180°,∠BAD∠BCD=∠BAC+∠CAD+∠ACB=180°,
∴∠DAC=∠B,
∴△ACB∽△DCA,
∴对角线AC是四边形ABCD的“完美对角线”.
一、单选题
1.下列图中,大小图形非相似图形的是( )
A. B. C. D.
2.下列说法正确的是( )
A.矩形都是相似图形
B.等边三角形都是相似三角形
C.各边对应成比例的多边形是相似多边形
D.边长相等的菱形都相似
3.下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
4.下面两个图形一定相似的是( )
A.两个等腰三角形 B.两个等腰直角三角形
C.两个菱形 D.两个矩形
二、填空题
5.下列说法中:①所有的等腰三角形都相似;②所有的正三角形都相似;③所有的正方形都相似;④所有的矩形都相似;⑤所有的圆都相似.其中说法正确的序号是 .
6.如果四边形ABCD的四条边长分别为54cm、48cm、45cm、63cm,另一个和它相似的四边形的最长边长为21cm,那么这个四边形的最短边的长度为 .
7.用4倍的放大镜看一个20°的角,则看出的角的度数是 .
8.如图,四边形ABCD~四边形EFGH,∠A=80°,∠F=70°,∠G=90°,则∠D= .
三、解答题
9.如图所示的各组中的两个图形,哪些是形状相同的图形?简单说明理由.
10.如图,将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?
11.如图左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形,和你的伙伴交流一下,看看谁的方法又快又好.
12.在下面两组图形中,每组的两个三角形相似,试分别确定α,x的值.
13.四边形∽四边形,,,若四边形的面积为12,求四边形的面积.
14.如图所示,一般书本的纸张是原纸张多次对开(对折)得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,求的值.
15.如图,四边形四边形.
(1)______.
(2)求的值.
16.如图在矩形中,,,、分别是、上的点,且,两动点、都以2cm/s的速度分别从、两点沿、向、两点运动,判断当、运动多长时间能使矩形与矩形相似,并证明你的结论.
17.将下列图形分别分成四小块,使它们得的形状大小完全相同,并且与原图形相似,应怎样分?(画出大致图形即可)
(1)
(2)
18.形状相同(即长与宽之比相等)的矩形是相似矩形,已知一个矩形长为,宽为1.
一分为二
(1)如图1,将矩形分割为一个正方形(阴影部分)和小矩形,小矩形恰与原矩形相似,则的值为______.
(2)如图2,将矩形分割为两个矩形,使每个小矩形均与原矩形相似,则的值为______.
一分为多
(3)有同学说“无论为何值,该矩形总可以分割为几个小矩形,这几个小矩形都与原矩形相似”,你同意这个说法吗?若同意,在图3中画出一种可行的分割方案;若不同意,举出反例.
一分为三
(4)将矩形分割为三个矩形,使每个小矩形均与原矩形相似.画出所有可能的分割方案的示意图,并在每个示意图下方直接写出对应的的值.
19.如图:矩形ABCD的长AB=30,宽BC=20.
(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;
(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?
20.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).
(1)当n=5时,共向外作出了 个小等边三角形,每个小等边三角形的面积为 ;
(2)当n=k时,共向外作出了 个小等边三角形,这些小等边三角形的面积和为 (用含k的式子表示).
21.如果四边形的一条对角线把这个四边形分成两个三角形并且相似(不全等),我们就把这条对角线称为“完美对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时,求证:对角线BD是四边形ABCD的“完美对角线.
(2)如图2,在四边形ABCD中,AC平分∠BCD,当∠BAD与∠BCD满足什么关系时,对角线AC是四边形ABCD的“完美对角线”?请说明理由.
参考答案
一、单选题
1.
【分析】根据相似图形的定义可知.
【解答】解:观察图形可知,A、B、C中的两个图形都是相似图形,D中的两个图形不是相似图形.
故选:D.
2.
【分析】各边对应成比例,各角对应相等的多边形是相似多边形,由此即可判断.
【解答】解:A、矩形的长和宽不一定对应成比例,矩形不一定都相似,故A不符合题意;
B、等边三角形的三边对应成比例,等边三角形都是相似三角形,故B符合题意;
C、多边形各边对应成比例,但多边形的各角不一定对应相等,各边对应成比例的多边形不一定是相似多边形,故C不符合题意;
D、菱形的各角不一定对应相等,边长相等的菱形不一定都相似,故D不符合题意.
故选:B.
3.
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
【解答】解:观察可得:甲和丁对应角相等,对应边成比例,且形状相同,大小不同,
故选:D.
4.
【分析】根据相似三角形的判定依据等腰直角三角形的性质判断即可.
【解答】解:两个等腰直角三角形一定相似,
故选:B.
二、填空题
5.
【分析】直接利用相似图形的定义得出答案.
【解答】解:①所有的等腰三角形都相似,错误,对应边不一定成比例,对应角不一定相等;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误,对应边不一定成比例;
⑤所有的圆都相似,正确.
故答案为:②③⑤.
6.
【分析】设这个四边形的最短边的长度为x cm,然后根据相似多边形的性质可得,从而进行计算即可解答.
【解答】解:设这个四边形的最短边的长度为x cm,
由题意得:
,
解得:x=15,
∴这个四边形的最短边的长度为15cm,
故答案为:15cm.
7.
【分析】角的大小是指两边张开的大小,与两条边的张开程度有关,用放大4倍的放大镜看一个20°的角,也就是把边变长了,而两边张开的大小没变,即角的度数没变,
【解答】解:用一个放大4倍的放大镜看一个20度的角,看到的这个角仍是20度;
故答案为:20°.
8.
【分析】根据相似多边形的对应角相等求解即可.
【解答】解:∵四边形ABCD~四边形EFGH,
∴∠F=∠B=70°,∠G=∠C=90°,
∵∠A=80°,
∴∠D=360°﹣∠A﹣∠B﹣∠C=120°,
故答案为:120°.
三、解答题
9.解:②和③中的两个图形经过放大或缩小得到另一个图形,所以它们的形状相同.
10.解:作图如下:
11.解:本题答案不唯一
12.解:图1中,在△ABC中,∠C=180°﹣∠A﹣∠B=50°,
∴α=50°,
∵△ABC∽△A′B′C′,
∴,
∴,
∴A′C′=3.78,
∴x=AC=3.78.
图2中,∵∠AOB=∠COD=60°,
∴∠A=180°﹣∠B﹣∠AOB=50°,
∴α=50°,
∵△ABO∽DCO,
∴,
∴,
∴AB=8,
∴x=8.
13.解:∵四边形∽四边形,,,
∴四边形与四边形的相似比为,
∴,即,
∴.
14.设,,则,,
由相似图形的性质得:,即,
解得或(不符题意,舍去),
则.
15.(1)解:∵四边形四边形,
∴,,
∵,
∴,
故答案为:;
(2)解:∵四边形四边形,
∴,即,
解得.
16.解:设运动时间能使矩形与矩形相似,
由题意或,
解得:或.
当时,,
∵,
又∵与都是矩形,
∴矩形与矩形相似.
同理可证当时矩形与矩形相似.
17.(1)解:作图如下:
(2)解:作图如下:
18.解:(1)由图可知阴影正方形的边长为1,
∴小长方形的宽为,长为1,
∵小矩形与原矩形相似,
∴,
∴,
解得:或(边长不能为负舍去),
∴;
(2)∵两小矩形的长都为1,且与原矩形的长宽比相同,
∴,
∴,
解得:或(舍去),
∴;
(3)同意,如下图连接矩形的四条边的中点,将矩形分为4个小矩形,
四个小矩形的长和宽都为和,长宽比为与原矩形长宽比相同;
(4)共有四种情况:
①如下图沿原矩形的长3等分,
小矩形和原矩形的长宽比都为a,
小矩形的长为1,则宽为,
∴,
∴,
解得:或(舍去),
∴;
②如下图先将矩形分割为两个小矩形,再将右边矩形两等分使宽都为,
根据原矩形的长宽比可得:
左边矩形的宽为,右边矩形的长为,
∴,
∴,
解得:或(舍去),
∴;
③如下图先将矩形分割为两个小矩形,再将右边矩形两等分使长都为,
根据原矩形的长宽比可得:
左边矩形的宽为,右边矩形的宽为,
∴∴,
∴,
解得:或(舍去),
∴;
④如下图先将矩形分割为两个小矩形,再将右边矩形分割为两个小矩形使两个矩形的长与宽的和为1,
根据原矩形的长宽比可得:
左边矩形的宽为,
∴右边两矩形的宽和长为,
∴右上矩形的长为,右下矩形的宽为,
∴,
∴,
设,则,
∴,
解得:或(舍去),
∴,
∴;
19.解:(1)不相似,理由如下:
AB=30,A′B′=28,BC=20,B′C′=18,
而,
∴图中两个矩形不相似;
(2)矩形ABCD与A′B′C′D′相似,则,
则:,
解得x=1.5,
或,
解得x=9.
综上所述,x=1.5或9时,图中的两个矩形相似.
20.解:(1)当n=5时,共有3×(5﹣2)=9个小等边三角形,
∴每个小三角形与大三角形边长的比,
∵大三角形的面积是S,
∴每个小三角形的面积为;‘
(2)由(1)可知,当n=k时,共有3×(k﹣2)=3(k﹣2),每个小三角形的面积为.
21.(1)证明:如图1中,
∵AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC∠ABC=35°,
∵∠ADC+∠C=180°,∠ADC=145°,
∴∠C=35°,
∴∠ADB=∠ABD=∠DBC=∠C=35°,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“完美对角线”.
(2)解:如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“完美对角线”.
理由:∵AC平分∠BCD,
∴∠ACB=∠ACD,
∵∠B+∠ACB+∠BAC=180°,∠BAD∠BCD=∠BAC+∠CAD+∠ACB=180°,
∴∠DAC=∠B,
∴△ACB∽△DCA,
∴对角线AC是四边形ABCD的“完美对角线”.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
