6.5 相似三角形的性质(含解析)苏科版九年级数学下册
文档属性
| 名称 | 6.5 相似三角形的性质(含解析)苏科版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 00:00:00 | ||
图片预览




文档简介
6.5 相似三角形的性质
一、单选题
1.在△ABC中,DE∥BC,AD:DB=1:2,则△ADE的面积:△BCD的面积=( )
A.1:6 B.1:4 C.2:3 D.1:3
2.如图,在矩形ABCD中,AB=6,BC=8,点E、F分别是BD、CD边上一点,连接AE、AF,BD交AF于点G,若BE=3,∠EAF=∠ABD,则DG的长为( )
A. B. C. D.
3.如图,在四边形ABCD中,对角线AC平分∠BAD,点E在AC上,分别连接BE,DE.若ED⊥AD,BC⊥AC,,∠ABE=30°,则BC:BE的值为( )
A. B. C. D.
4.如图,矩形ABCD的边长AB=2,AD=3,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. B. C. D.
5.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为( )
A. B. C. D.
二、填空题
6.如图,AB与CD交于点O,且AC∥BD.若,则 .
7.如图,在△ABC中,DE∥BC,联结BE,如果△ADE和△BEC的面积都为1,则△DEB的面积为 .
8.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为 .
9.如图,在Rt△ABC中,∠BAC=90°,BD是△ABC的一条角平分线,过点A作AE⊥BC交BC于点E,交BD于点F.若,△AFD的面积为 ,则BE= .
10.如图,点C是以AB为直径的半圆上的三等分点(BC<AC),点E为上一动点,(不与点A、C重合),过点B作BF⊥AB与EC的延长线交于点F,过点B作BG⊥OC于点G,交EC于点H,若OG=2,H为CE的三等分点,EH的长为 .
11.如图,在矩形ABCD中,AB=8,AD=4,连接AC,点E,F分别在边AD,CD上,连接BE,BF分别交AC于点M,N.若∠EBF=45°,CF=2,则DE的长为 .
三、解答题
12.如图,在菱形ABCD中,过D作DE⊥BC交BC的延长线于点E,过E作EF⊥AB交AB于点F.
(1)求证△DEC∽△EFB;
(2)若BC=6,CE=2,求AF的长.
13.如图,已知AB是⊙O的直径,点C是的中点,点D是的中点,连接AC,BC,AD,AD与BC交于点E,过点D作DF⊥AC于点F.
(1)求证:DF为⊙O的切线;
(2)若,求AD的长度.
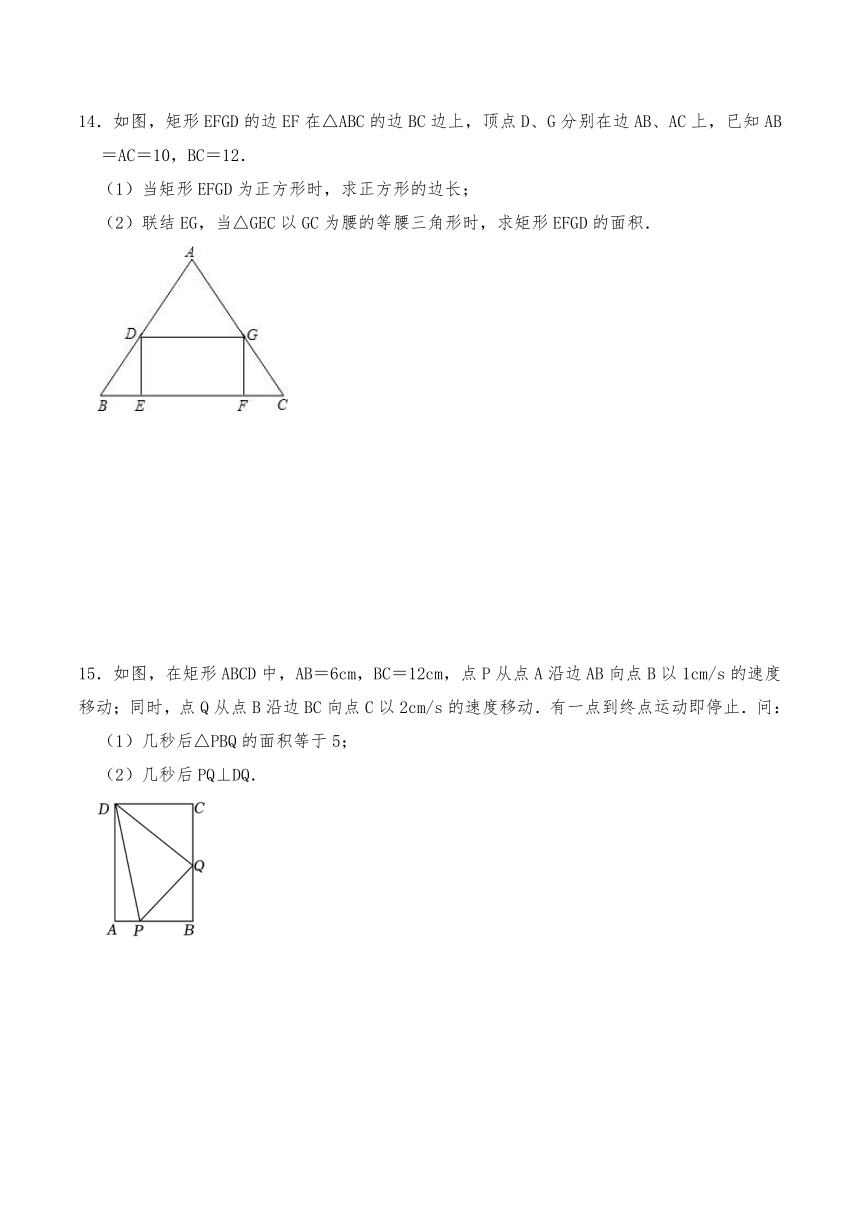
14.如图,矩形EFGD的边EF在△ABC的边BC边上,顶点D、G分别在边AB、AC上,已知AB=AC=10,BC=12.
(1)当矩形EFGD为正方形时,求正方形的边长;
(2)联结EG,当△GEC以GC为腰的等腰三角形时,求矩形EFGD的面积.
15.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.有一点到终点运动即停止.问:
(1)几秒后△PBQ的面积等于5;
(2)几秒后PQ⊥DQ.
16.如图,在Rt△ABC中,∠ACB=90°,D是BC上一点,过点C作CE⊥AD,垂足为E.连接BE并延长交AC于点F.
(1)求证:CD2=ED AD;
(2)已知D为BC的中点,求证:∠DBE=∠DAB.
17.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=8,BM=6,求AE的长.
18.如图,在△ABC和△ADE中,AB=mAC,AD=mAE(m>1),∠BAC=∠DAE,连接BD,CE交于点O.求证:
(1)△ABD∽△ACE;
(2)∠BAC=∠BOC.
19.如图,在中,,为延长线上一点,,,过作,交的延长线于点.
(1)求证:.
(2)求长度.
20.如图,平分,.
(1)求证:;
(2)若,,求的长.
参考答案
一、单选题
1.
【分析】由AD:DB=1:2,推导出,由DE∥BC证明△ADE∽△ABC,得,则()2,求得S△ADC=3,S△ABC=9,所以S△BCD=6,于是得到问题的答案.
【解答】解:∵AD:DB=1:2,
∴,
∵DE∥BC,△ADE的面积为1,
∴△ADE∽△ABC,
∴,
∴,
∴S△ADC=3S△ADE=3×1=3,S△ABC=9S△ADE=9×1=9,
∴S△BCD=S△ABC﹣S△ADC=9﹣3=6,
∴△ADE的面积:△BCD的面积=1:6,
故选:A.
2.
【分析】连接AC,交BD于点O,先证明∠BAE=∠CAF,∠ACF=∠BAC=∠ABD,进而可得△ABE∽△ACF,由,求出CF=5,DF=1,再由△ABE∽△ACF,得,即可求出DG的长.
【解答】解:在矩形ABCD中,AB=6,BC=8,点E、F分别是BD、CD边上一点,连接AC,交BD于点O;
∴AB=CD=6,∠BAD=90°,
在直角三角形ABD中,,
∴OA=OB=OC=OD=5,
∴∠ABD=∠BAC,
∵∠EAF=∠ABD,
∴∠BAC=∠EAF,
∴∠BAE+∠EAC=∠CAF+∠CAE,
∴∠BAE=∠CAF.
∵AB∥CD,
∴∠ACF=∠BAC=∠ABD,
∴△ABE∽△ACF,
∴,即,
解得:CF=5,
∴DF=CD﹣CF=6﹣5=1,
∵AB∥CD,
∴△ABG∽△FDG,
∴,
∴,
解得:,
故选:C.
3.
【分析】过点E作EF⊥AB,垂足为F,根据角平分线的性质可得∠DAE=∠CAB,EF=ED,再根据垂直定义可得∠BCA=∠EDA=90°,从而证明△ADE∽△ACB,然后利用相似三角形的性质可得,最后再根据含30度角的直角三角形,进行计算即可解答.
【解答】解:过点E作EF⊥AB,垂足为F,
∵ED⊥AD,AC平分∠BAD,
∴EF=ED,∠DAE=∠CAB,
∵BC⊥AC,
∴∠EDA=∠BCA=90°,
∴△ADE∽△ACB,
∴,
∴,
∵∠ABE=30°,∠EFB=90°,
∴BE=2EF,
∴,
故选:A.
4.
【分析】首先过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理求得AF,根据平行线分线段成比例定理求得OH,由相似三角形的性质求得AM与AF的长,根据相似三角形的性质,求得AN的长,即可得到结论.
【解答】解:过F作FH⊥AD于H,交ED于O,则FH=AB=2,
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF2,
∵OH∥AE,
∴,
∴OHAE,
∴OF=FH﹣OH=2,
∵AE∥FO,
∴△AME∽FMO,
∴,
∴AMAF,
∵AD∥BF,
∴△AND∽△FNB,
∴,
∴ANAF,
∴MN=AN﹣AM.
故选:D.
5.
【分析】先利用菱形的性质得到AB=CD=AD=3,∠ABC=ADC=60°,AB∥CD,则∠EAD=60°,∠ABD=30°,再在Rt△ADE中计算出AE,DE,则利用勾股定理可计算出CE,接着证明△BEG∽△DCG,利用相似三角形的性质和比例的性质得到EG,利用同样方法可计算出EF,然后计算EG﹣EF即可.
【解答】解:∵四边形ABCD为菱形,
∴AB=CD=AD=3,∠ABC=ADC=60°,AB∥CD,
∴∠EAD=∠ADC=60°,∠ABD∠ABC=30°,
∵DE⊥AB,
∴∠DEB=∠EDC=90°,
在Rt△ADE中,∵AEAD,
∴DEAE,
在Rt△CDE中,CE,
∵BE∥CD,
∴△BEG∽△DCG,
∴,
∴,
∴EG,
∵AE∥CD,
∴△AEF∽△DCF,
∴,
∴,
∴EF,
∴FG=EG﹣EF.
故选:B.
二、填空题
6.
【分析】根据AC∥BD.可以得到△AOC∽△BOD,然后相似三角形的相似比等于周长之比,即可得到的值.
【解答】解:∵AC∥BD.
∴△AOC∽△BOD,
∴,
∵,
∴,
故答案为:.
7.
【分析】设△DEB的面积为S,利用三角形面积公式得到,则利用比例性质得到,再证明△ADE∽△ABC,则根据相似三角形的性质得()2,整理得S2+S﹣1=0,然后解方程求出S即可.
【解答】解:设△DEB的面积为S,
∵,
∴,
∴,
即,
∵DE∥BC,
∴△ADE∽△ABC,
∴()2,
∴()2,
整理得S2+S﹣1=0,
解得S1,S2(舍去),
即△DEB的面积为.
故答案为:.
8.
【分析】由DE⊥AB,得∠AED=90°,因为四边形ABCD是边长为3的菱形,∠ADC=60°,所以AD=AB=CD=3,AB∥CD,则∠EDC=90°,∠ADE=30°,所以EAAD,求得EB,DE2=AD2﹣EA2,则CE,可证明△CDG∽△EBG,得,则CGCE,再证明△EAF∽△CDF,得,则EFCE,即可求得FG,于是得到问题的答案.
【解答】解:∵DE⊥AB,交BA的延长线于点E,
∴∠AED=90°,
∵四边形ABCD是边长为3的菱形,∠ADC=60°,
∴AD=AB=CD=3,AB∥CD,
∴∠EDC=180°﹣∠AED=90°,
∴∠ADE=90°﹣∠ADC=30°,
∴EAAD,
∴EB=EA+AB3,DE2=AD2﹣EA2=32,
∴CE,
∵CD∥EB,
∴△CDG∽△EBG,
∴,
∴CGCECE,
∵EA∥CD,
∴△EAF∽△CDF,
∴,
∴EFCECE,
∴FG=CE﹣CG﹣EF,
故答案为:.
9.
【分析】过点A作AG⊥DF于点G,先证出△AFD是等腰三角形,从而得到,设参,设DG=FG=x,AD=AF=y,再证△DAG∽△DBA,得到,代入x、y得到y=3x,进而利用面积求出x值,进而得解.
【解答】解:过点A作AG⊥DF于点G,则∠AGF=∠AGD=90°,
∵AE⊥BC,
∴∠AEB=90°,
∵∠BAC=90°,
∴∠ABC=∠EAC=90°﹣∠BAE,
∵∠AFG=∠BFE,∠AGF=∠BEF=90°,
∴△GAF∽△EBF,
∴∠EBF=∠GAF,,
∵BD平分∠ABC,
∴∠EBFABC,
∴∠GAF∠EAC,
即∠GAF=∠GAD,
∵AG=DG,
∴△AGF≌△AGD(ASA),
∴GF=GDDF,AF=AD,
∵,
∴,
设DG=FG=x,AD=AF=y,
则BFy,
∴BDy+2x,
∵,∠AGD=∠ABC=90°,
∴△DAG∽△DBA,
∴,
即,
整理得y=3x,
∴AD=AF=3x,
根据勾股定理可得AG=2x,
∴S△AFDDF AG=2x2=18,
解得x=3(负值舍去),
∴AG=6,
∵,
∴BE=14.
故答案为:14.
10.
【分析】先证△OBC为等边三角形,得到∠COB=∠OBC=∠OCB=60°,进而得到∠CEB=∠CBG=30°,证△BCE∽△HCB,得到CE CH=BC2=16,然后分类讨论计算即可得解.
【解答】解:∵点C是以AB为直径的半圆上的三等分点(BC<AC),
∴∠BOC=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴∠COB=∠OBC=∠OCB=60°,
∵,
∴∠CEB∠COB=30°,
∵BG⊥OC,
∴OC=CGOC,∠OBG=∠CBG=30°,
∵OG=2,
∴OC=4=BC=OB,
∵∠CEB=∠CBG=30°,∠BCE=∠HCB,
∴△BCE∽△HCB,
∴,
∴CE CH=BC2=16,
∵H为CE的三等分点,
∴可以分两种情况讨论,设CE=3x,
①EH时,则EH=x,CH=2x,
∴2x 3x=16,
解得x(负值舍去),
∴EH,
②EHCE时,EH=2x,CH=x,
∴x 3x=16,
解得x,
∴EH=2x;
综上,EH的长为或.
故答案为:或.
11.
【分析】根据矩形的性质和勾股定理求出BF,证明△CFN∽△ABN,求出BN,再证明△BCF∽△ABC,△BCN∽△ABC,△AME∽△CBM,对应边成比例即可解决问题.
【解答】解:在矩形ABCD中,AD=4,
∴BC=AD=4,
∵CF=2,
在Rt△CBF中,BF2,
∵CD∥AB,
∴△CFN∽△ABN,
∴,
∵AB=CD=8,FN=FB﹣BN=2BN,
∴,
∴BN,
∵四边形ABCD是矩形,
∴∠ABC=90°,AB∥CD,
∵AB=8,AD=4,
由勾股定理得:AC4,
∵AB=8,BC=AD=4,CF=2,
∴,
∵∠BCF=∠ABC=90°,
∴△BCF∽△ABC,
∴∠CBF=∠BAC,
∵∠BAC+∠ACB=90°,
∴∠CBF+∠ACB=90°,
∴∠CNB=90°,
∴CA⊥BF,
∵∠EBF=45°,
∴∠BMN=45°,
∴MN=BN,
∵∠CBF=∠BAC,∠BNC=∠ABC=90°,
∴△BCN∽△ABC,
∴,
∴CNBN,
∴AB=AC﹣MN﹣CN=4,CM=CN+MN,
∵AD∥BC,
∴△AME∽△CBM,
∴,
∴,
∴AE,
∴DE=AD﹣AE=4.
故答案为:.
三、解答题
12.(1)证明:∵四边形ABCD是菱形,
∴CD∥AB,
∴∠DCE=∠EBF,
∵DE⊥BC交BC的延长线于点E,EF⊥AB于点F,
∴∠DEC=∠EFB=90°,
∴△DEC∽△EFB.
(2)解:∵BC=6,CE=2,
∴AB=CD=BC=6,BE=BC+CE=6+2=8,
∵△DEC∽△EFB,
∴,
∴BF,
∴AF=AB﹣BF=6,
∴AF的长是.
13.(1)证明:如图1,连接OD交BC于点G,
∵AB是⊙O的直径,DF⊥AC于点F,
∴∠ACB=∠F=90°,
∴DF∥BC,
∵点D是的中点,
∴OD垂直平分BC,
∴∠ODF=∠OGC=90°,
∵OD是⊙O的半径,且DF⊥OD,
∴DF为⊙O的切线.
(2)解:如图2,连接CD,作EI⊥CD于点I,CH⊥CB于点H,则∠DIE=∠DHC=90°,
∵点C是的中点,点D是的中点,
∴,,
∵∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠ADC=∠B=45°,∠BCD=∠CAD=∠BAD∠CAB=22.5°,
∴∠IED=∠IDE=∠HCD=45°,
∴ID=IE,CH=DH,∠BCD=∠BCH=22.5°,
∴IE=HE,
∵DEIE=22,
∴IE=HI=2,
∴DH=DE+IE=22+2,
∴CD2=CH2+DH2=2DH2=2×()2=4,
∵∠ECD=∠CAD,∠CDE=∠ADC,
∴△CDE∽△ADC,
∴,
∴AD22,
∴AD的长是22.
14.解:(1)如图,过点A作AH⊥BC于H,交DG于O,
∵AB=AC=10,BC=12,
∴BH,
∴AH8,
∵四边形EFGD为正方形,设DE=x,
∴DG=x,AO=8﹣x,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
解得:x,
∴正方形的边长为;
(2)当GC=GE时,如图,作AH⊥BC于H,
∴EF=CF,
∵AB=AC,
∴∠B=∠C,
∵∠BED=∠CFG,DE=FG,
∴△BDE≌△CGF(AAS),
∴BE=CF=EF=4,
∴GFCF,
∴S矩形DEFG=4;
当CE=CG时,如图,作AH⊥BC于H,
设BE=CF=x,则CG=CE=12﹣x,
∴,
∴,
解得x,
∴CF,
∴GFCF,
∴S矩形DEFG=6×3=18,
综上:矩形EFGD的面积为或18.
15.解:(1)设x秒后△PBQ的面积等于5cm2.
则AP=x cm,QB=2x cm,
∴PB=(6﹣x)cm,
∴(6﹣x)2x=5,
解得x1=1,x2=5,
答:1秒或5秒后△PBQ的面积等于5cm2;
(2)设y秒后PQ⊥DQ,则∠DQP为直角,
∴∠BQP+∠DQC=90°,
∵四边形ABCD是矩形,
∴∠C=∠B=90°,
∴∠BQP+∠QPB=90°,
∴∠DQC=∠QPB,
∴△BPQ∽△CQD,
∴,
设AP=y cm,QB=2y cm,
∴,
∴2y2﹣15y+18=0,
解得:y或6,
经检验y是原分式方程的根,y=6不是原分式方程的根,
当y=6时,P点到达B点、Q点到达C点,此时PQ⊥DQ.
答:秒或6秒后PQ⊥DQ.
16.(1)证明:∵CE⊥AD,∠ACB=90°,
∴∠DEC=∠ACB=90°,
又∵∠EDC=∠CDA,
∴△DCE∽△DAC中,
∴,
∴CD2=ED AD;
(2)证明:∵点D为BC的中点,
∴BD=CD,
∴CD2=ED AD,
∴BD2=ED AD,
即,
又∵∠BDE=∠ADB,
∴△DEB∽△DBA,
∴∠DBE=∠DAB.
17.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵四边形ABCD是正方形,AB=8,BM=6,
∴∠B=90°,AD=AB=8,
∴,
∵F是AM的中点,
∴,
∵△ABM∽△EFA,
∴,
即,
∴.
18.证明:(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
∵AB=mAC,AD=mAE,
∴m,m,
∴,
∴,
又∵∠BAC=∠DAE,
∴△ABD∽△ACE;
(2)设AC与BD交于点F,如图所示:
∵△ABD∽△ACE;
∴∠ABD=∠ACE,
∵∠ABD+∠AFB+∠BAC=180°,∠ACE+∠CFO+∠BOC=180°,
又∵∠AFB=∠CFO,
∴∠BAC=∠BOC.
19.解:(1)证明:,
,
,
,又,
;
(2),
,
,
,
,
,
由(1)知,
,
,
(负值舍去).
答:的长度为2.
20.(1)解:平分,
.
,
;
(2),
.
,,
.
一、单选题
1.在△ABC中,DE∥BC,AD:DB=1:2,则△ADE的面积:△BCD的面积=( )
A.1:6 B.1:4 C.2:3 D.1:3
2.如图,在矩形ABCD中,AB=6,BC=8,点E、F分别是BD、CD边上一点,连接AE、AF,BD交AF于点G,若BE=3,∠EAF=∠ABD,则DG的长为( )
A. B. C. D.
3.如图,在四边形ABCD中,对角线AC平分∠BAD,点E在AC上,分别连接BE,DE.若ED⊥AD,BC⊥AC,,∠ABE=30°,则BC:BE的值为( )
A. B. C. D.
4.如图,矩形ABCD的边长AB=2,AD=3,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. B. C. D.
5.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为( )
A. B. C. D.
二、填空题
6.如图,AB与CD交于点O,且AC∥BD.若,则 .
7.如图,在△ABC中,DE∥BC,联结BE,如果△ADE和△BEC的面积都为1,则△DEB的面积为 .
8.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为 .
9.如图,在Rt△ABC中,∠BAC=90°,BD是△ABC的一条角平分线,过点A作AE⊥BC交BC于点E,交BD于点F.若,△AFD的面积为 ,则BE= .
10.如图,点C是以AB为直径的半圆上的三等分点(BC<AC),点E为上一动点,(不与点A、C重合),过点B作BF⊥AB与EC的延长线交于点F,过点B作BG⊥OC于点G,交EC于点H,若OG=2,H为CE的三等分点,EH的长为 .
11.如图,在矩形ABCD中,AB=8,AD=4,连接AC,点E,F分别在边AD,CD上,连接BE,BF分别交AC于点M,N.若∠EBF=45°,CF=2,则DE的长为 .
三、解答题
12.如图,在菱形ABCD中,过D作DE⊥BC交BC的延长线于点E,过E作EF⊥AB交AB于点F.
(1)求证△DEC∽△EFB;
(2)若BC=6,CE=2,求AF的长.
13.如图,已知AB是⊙O的直径,点C是的中点,点D是的中点,连接AC,BC,AD,AD与BC交于点E,过点D作DF⊥AC于点F.
(1)求证:DF为⊙O的切线;
(2)若,求AD的长度.
14.如图,矩形EFGD的边EF在△ABC的边BC边上,顶点D、G分别在边AB、AC上,已知AB=AC=10,BC=12.
(1)当矩形EFGD为正方形时,求正方形的边长;
(2)联结EG,当△GEC以GC为腰的等腰三角形时,求矩形EFGD的面积.
15.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.有一点到终点运动即停止.问:
(1)几秒后△PBQ的面积等于5;
(2)几秒后PQ⊥DQ.
16.如图,在Rt△ABC中,∠ACB=90°,D是BC上一点,过点C作CE⊥AD,垂足为E.连接BE并延长交AC于点F.
(1)求证:CD2=ED AD;
(2)已知D为BC的中点,求证:∠DBE=∠DAB.
17.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=8,BM=6,求AE的长.
18.如图,在△ABC和△ADE中,AB=mAC,AD=mAE(m>1),∠BAC=∠DAE,连接BD,CE交于点O.求证:
(1)△ABD∽△ACE;
(2)∠BAC=∠BOC.
19.如图,在中,,为延长线上一点,,,过作,交的延长线于点.
(1)求证:.
(2)求长度.
20.如图,平分,.
(1)求证:;
(2)若,,求的长.
参考答案
一、单选题
1.
【分析】由AD:DB=1:2,推导出,由DE∥BC证明△ADE∽△ABC,得,则()2,求得S△ADC=3,S△ABC=9,所以S△BCD=6,于是得到问题的答案.
【解答】解:∵AD:DB=1:2,
∴,
∵DE∥BC,△ADE的面积为1,
∴△ADE∽△ABC,
∴,
∴,
∴S△ADC=3S△ADE=3×1=3,S△ABC=9S△ADE=9×1=9,
∴S△BCD=S△ABC﹣S△ADC=9﹣3=6,
∴△ADE的面积:△BCD的面积=1:6,
故选:A.
2.
【分析】连接AC,交BD于点O,先证明∠BAE=∠CAF,∠ACF=∠BAC=∠ABD,进而可得△ABE∽△ACF,由,求出CF=5,DF=1,再由△ABE∽△ACF,得,即可求出DG的长.
【解答】解:在矩形ABCD中,AB=6,BC=8,点E、F分别是BD、CD边上一点,连接AC,交BD于点O;
∴AB=CD=6,∠BAD=90°,
在直角三角形ABD中,,
∴OA=OB=OC=OD=5,
∴∠ABD=∠BAC,
∵∠EAF=∠ABD,
∴∠BAC=∠EAF,
∴∠BAE+∠EAC=∠CAF+∠CAE,
∴∠BAE=∠CAF.
∵AB∥CD,
∴∠ACF=∠BAC=∠ABD,
∴△ABE∽△ACF,
∴,即,
解得:CF=5,
∴DF=CD﹣CF=6﹣5=1,
∵AB∥CD,
∴△ABG∽△FDG,
∴,
∴,
解得:,
故选:C.
3.
【分析】过点E作EF⊥AB,垂足为F,根据角平分线的性质可得∠DAE=∠CAB,EF=ED,再根据垂直定义可得∠BCA=∠EDA=90°,从而证明△ADE∽△ACB,然后利用相似三角形的性质可得,最后再根据含30度角的直角三角形,进行计算即可解答.
【解答】解:过点E作EF⊥AB,垂足为F,
∵ED⊥AD,AC平分∠BAD,
∴EF=ED,∠DAE=∠CAB,
∵BC⊥AC,
∴∠EDA=∠BCA=90°,
∴△ADE∽△ACB,
∴,
∴,
∵∠ABE=30°,∠EFB=90°,
∴BE=2EF,
∴,
故选:A.
4.
【分析】首先过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理求得AF,根据平行线分线段成比例定理求得OH,由相似三角形的性质求得AM与AF的长,根据相似三角形的性质,求得AN的长,即可得到结论.
【解答】解:过F作FH⊥AD于H,交ED于O,则FH=AB=2,
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF2,
∵OH∥AE,
∴,
∴OHAE,
∴OF=FH﹣OH=2,
∵AE∥FO,
∴△AME∽FMO,
∴,
∴AMAF,
∵AD∥BF,
∴△AND∽△FNB,
∴,
∴ANAF,
∴MN=AN﹣AM.
故选:D.
5.
【分析】先利用菱形的性质得到AB=CD=AD=3,∠ABC=ADC=60°,AB∥CD,则∠EAD=60°,∠ABD=30°,再在Rt△ADE中计算出AE,DE,则利用勾股定理可计算出CE,接着证明△BEG∽△DCG,利用相似三角形的性质和比例的性质得到EG,利用同样方法可计算出EF,然后计算EG﹣EF即可.
【解答】解:∵四边形ABCD为菱形,
∴AB=CD=AD=3,∠ABC=ADC=60°,AB∥CD,
∴∠EAD=∠ADC=60°,∠ABD∠ABC=30°,
∵DE⊥AB,
∴∠DEB=∠EDC=90°,
在Rt△ADE中,∵AEAD,
∴DEAE,
在Rt△CDE中,CE,
∵BE∥CD,
∴△BEG∽△DCG,
∴,
∴,
∴EG,
∵AE∥CD,
∴△AEF∽△DCF,
∴,
∴,
∴EF,
∴FG=EG﹣EF.
故选:B.
二、填空题
6.
【分析】根据AC∥BD.可以得到△AOC∽△BOD,然后相似三角形的相似比等于周长之比,即可得到的值.
【解答】解:∵AC∥BD.
∴△AOC∽△BOD,
∴,
∵,
∴,
故答案为:.
7.
【分析】设△DEB的面积为S,利用三角形面积公式得到,则利用比例性质得到,再证明△ADE∽△ABC,则根据相似三角形的性质得()2,整理得S2+S﹣1=0,然后解方程求出S即可.
【解答】解:设△DEB的面积为S,
∵,
∴,
∴,
即,
∵DE∥BC,
∴△ADE∽△ABC,
∴()2,
∴()2,
整理得S2+S﹣1=0,
解得S1,S2(舍去),
即△DEB的面积为.
故答案为:.
8.
【分析】由DE⊥AB,得∠AED=90°,因为四边形ABCD是边长为3的菱形,∠ADC=60°,所以AD=AB=CD=3,AB∥CD,则∠EDC=90°,∠ADE=30°,所以EAAD,求得EB,DE2=AD2﹣EA2,则CE,可证明△CDG∽△EBG,得,则CGCE,再证明△EAF∽△CDF,得,则EFCE,即可求得FG,于是得到问题的答案.
【解答】解:∵DE⊥AB,交BA的延长线于点E,
∴∠AED=90°,
∵四边形ABCD是边长为3的菱形,∠ADC=60°,
∴AD=AB=CD=3,AB∥CD,
∴∠EDC=180°﹣∠AED=90°,
∴∠ADE=90°﹣∠ADC=30°,
∴EAAD,
∴EB=EA+AB3,DE2=AD2﹣EA2=32,
∴CE,
∵CD∥EB,
∴△CDG∽△EBG,
∴,
∴CGCECE,
∵EA∥CD,
∴△EAF∽△CDF,
∴,
∴EFCECE,
∴FG=CE﹣CG﹣EF,
故答案为:.
9.
【分析】过点A作AG⊥DF于点G,先证出△AFD是等腰三角形,从而得到,设参,设DG=FG=x,AD=AF=y,再证△DAG∽△DBA,得到,代入x、y得到y=3x,进而利用面积求出x值,进而得解.
【解答】解:过点A作AG⊥DF于点G,则∠AGF=∠AGD=90°,
∵AE⊥BC,
∴∠AEB=90°,
∵∠BAC=90°,
∴∠ABC=∠EAC=90°﹣∠BAE,
∵∠AFG=∠BFE,∠AGF=∠BEF=90°,
∴△GAF∽△EBF,
∴∠EBF=∠GAF,,
∵BD平分∠ABC,
∴∠EBFABC,
∴∠GAF∠EAC,
即∠GAF=∠GAD,
∵AG=DG,
∴△AGF≌△AGD(ASA),
∴GF=GDDF,AF=AD,
∵,
∴,
设DG=FG=x,AD=AF=y,
则BFy,
∴BDy+2x,
∵,∠AGD=∠ABC=90°,
∴△DAG∽△DBA,
∴,
即,
整理得y=3x,
∴AD=AF=3x,
根据勾股定理可得AG=2x,
∴S△AFDDF AG=2x2=18,
解得x=3(负值舍去),
∴AG=6,
∵,
∴BE=14.
故答案为:14.
10.
【分析】先证△OBC为等边三角形,得到∠COB=∠OBC=∠OCB=60°,进而得到∠CEB=∠CBG=30°,证△BCE∽△HCB,得到CE CH=BC2=16,然后分类讨论计算即可得解.
【解答】解:∵点C是以AB为直径的半圆上的三等分点(BC<AC),
∴∠BOC=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴∠COB=∠OBC=∠OCB=60°,
∵,
∴∠CEB∠COB=30°,
∵BG⊥OC,
∴OC=CGOC,∠OBG=∠CBG=30°,
∵OG=2,
∴OC=4=BC=OB,
∵∠CEB=∠CBG=30°,∠BCE=∠HCB,
∴△BCE∽△HCB,
∴,
∴CE CH=BC2=16,
∵H为CE的三等分点,
∴可以分两种情况讨论,设CE=3x,
①EH时,则EH=x,CH=2x,
∴2x 3x=16,
解得x(负值舍去),
∴EH,
②EHCE时,EH=2x,CH=x,
∴x 3x=16,
解得x,
∴EH=2x;
综上,EH的长为或.
故答案为:或.
11.
【分析】根据矩形的性质和勾股定理求出BF,证明△CFN∽△ABN,求出BN,再证明△BCF∽△ABC,△BCN∽△ABC,△AME∽△CBM,对应边成比例即可解决问题.
【解答】解:在矩形ABCD中,AD=4,
∴BC=AD=4,
∵CF=2,
在Rt△CBF中,BF2,
∵CD∥AB,
∴△CFN∽△ABN,
∴,
∵AB=CD=8,FN=FB﹣BN=2BN,
∴,
∴BN,
∵四边形ABCD是矩形,
∴∠ABC=90°,AB∥CD,
∵AB=8,AD=4,
由勾股定理得:AC4,
∵AB=8,BC=AD=4,CF=2,
∴,
∵∠BCF=∠ABC=90°,
∴△BCF∽△ABC,
∴∠CBF=∠BAC,
∵∠BAC+∠ACB=90°,
∴∠CBF+∠ACB=90°,
∴∠CNB=90°,
∴CA⊥BF,
∵∠EBF=45°,
∴∠BMN=45°,
∴MN=BN,
∵∠CBF=∠BAC,∠BNC=∠ABC=90°,
∴△BCN∽△ABC,
∴,
∴CNBN,
∴AB=AC﹣MN﹣CN=4,CM=CN+MN,
∵AD∥BC,
∴△AME∽△CBM,
∴,
∴,
∴AE,
∴DE=AD﹣AE=4.
故答案为:.
三、解答题
12.(1)证明:∵四边形ABCD是菱形,
∴CD∥AB,
∴∠DCE=∠EBF,
∵DE⊥BC交BC的延长线于点E,EF⊥AB于点F,
∴∠DEC=∠EFB=90°,
∴△DEC∽△EFB.
(2)解:∵BC=6,CE=2,
∴AB=CD=BC=6,BE=BC+CE=6+2=8,
∵△DEC∽△EFB,
∴,
∴BF,
∴AF=AB﹣BF=6,
∴AF的长是.
13.(1)证明:如图1,连接OD交BC于点G,
∵AB是⊙O的直径,DF⊥AC于点F,
∴∠ACB=∠F=90°,
∴DF∥BC,
∵点D是的中点,
∴OD垂直平分BC,
∴∠ODF=∠OGC=90°,
∵OD是⊙O的半径,且DF⊥OD,
∴DF为⊙O的切线.
(2)解:如图2,连接CD,作EI⊥CD于点I,CH⊥CB于点H,则∠DIE=∠DHC=90°,
∵点C是的中点,点D是的中点,
∴,,
∵∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠ADC=∠B=45°,∠BCD=∠CAD=∠BAD∠CAB=22.5°,
∴∠IED=∠IDE=∠HCD=45°,
∴ID=IE,CH=DH,∠BCD=∠BCH=22.5°,
∴IE=HE,
∵DEIE=22,
∴IE=HI=2,
∴DH=DE+IE=22+2,
∴CD2=CH2+DH2=2DH2=2×()2=4,
∵∠ECD=∠CAD,∠CDE=∠ADC,
∴△CDE∽△ADC,
∴,
∴AD22,
∴AD的长是22.
14.解:(1)如图,过点A作AH⊥BC于H,交DG于O,
∵AB=AC=10,BC=12,
∴BH,
∴AH8,
∵四边形EFGD为正方形,设DE=x,
∴DG=x,AO=8﹣x,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
解得:x,
∴正方形的边长为;
(2)当GC=GE时,如图,作AH⊥BC于H,
∴EF=CF,
∵AB=AC,
∴∠B=∠C,
∵∠BED=∠CFG,DE=FG,
∴△BDE≌△CGF(AAS),
∴BE=CF=EF=4,
∴GFCF,
∴S矩形DEFG=4;
当CE=CG时,如图,作AH⊥BC于H,
设BE=CF=x,则CG=CE=12﹣x,
∴,
∴,
解得x,
∴CF,
∴GFCF,
∴S矩形DEFG=6×3=18,
综上:矩形EFGD的面积为或18.
15.解:(1)设x秒后△PBQ的面积等于5cm2.
则AP=x cm,QB=2x cm,
∴PB=(6﹣x)cm,
∴(6﹣x)2x=5,
解得x1=1,x2=5,
答:1秒或5秒后△PBQ的面积等于5cm2;
(2)设y秒后PQ⊥DQ,则∠DQP为直角,
∴∠BQP+∠DQC=90°,
∵四边形ABCD是矩形,
∴∠C=∠B=90°,
∴∠BQP+∠QPB=90°,
∴∠DQC=∠QPB,
∴△BPQ∽△CQD,
∴,
设AP=y cm,QB=2y cm,
∴,
∴2y2﹣15y+18=0,
解得:y或6,
经检验y是原分式方程的根,y=6不是原分式方程的根,
当y=6时,P点到达B点、Q点到达C点,此时PQ⊥DQ.
答:秒或6秒后PQ⊥DQ.
16.(1)证明:∵CE⊥AD,∠ACB=90°,
∴∠DEC=∠ACB=90°,
又∵∠EDC=∠CDA,
∴△DCE∽△DAC中,
∴,
∴CD2=ED AD;
(2)证明:∵点D为BC的中点,
∴BD=CD,
∴CD2=ED AD,
∴BD2=ED AD,
即,
又∵∠BDE=∠ADB,
∴△DEB∽△DBA,
∴∠DBE=∠DAB.
17.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵四边形ABCD是正方形,AB=8,BM=6,
∴∠B=90°,AD=AB=8,
∴,
∵F是AM的中点,
∴,
∵△ABM∽△EFA,
∴,
即,
∴.
18.证明:(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
∵AB=mAC,AD=mAE,
∴m,m,
∴,
∴,
又∵∠BAC=∠DAE,
∴△ABD∽△ACE;
(2)设AC与BD交于点F,如图所示:
∵△ABD∽△ACE;
∴∠ABD=∠ACE,
∵∠ABD+∠AFB+∠BAC=180°,∠ACE+∠CFO+∠BOC=180°,
又∵∠AFB=∠CFO,
∴∠BAC=∠BOC.
19.解:(1)证明:,
,
,
,又,
;
(2),
,
,
,
,
,
由(1)知,
,
,
(负值舍去).
答:的长度为2.
20.(1)解:平分,
.
,
;
(2),
.
,,
.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
