6.7用相似三角形解决问题(含解析)苏科版九年级数学下册
文档属性
| 名称 | 6.7用相似三角形解决问题(含解析)苏科版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 967.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 12:07:36 | ||
图片预览

文档简介
6.7用相似三角形解决问题
一、单选题
1.如图,在△ABC中,∠ABC=90°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1.5cm,则AD的长为( )
A. B. C. D.
2.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=6m,BP=8m,PD=18m,那么该古城墙CD的高度是( )m.
A.12 B.10 C.13.5或24 D.13.5
3.《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
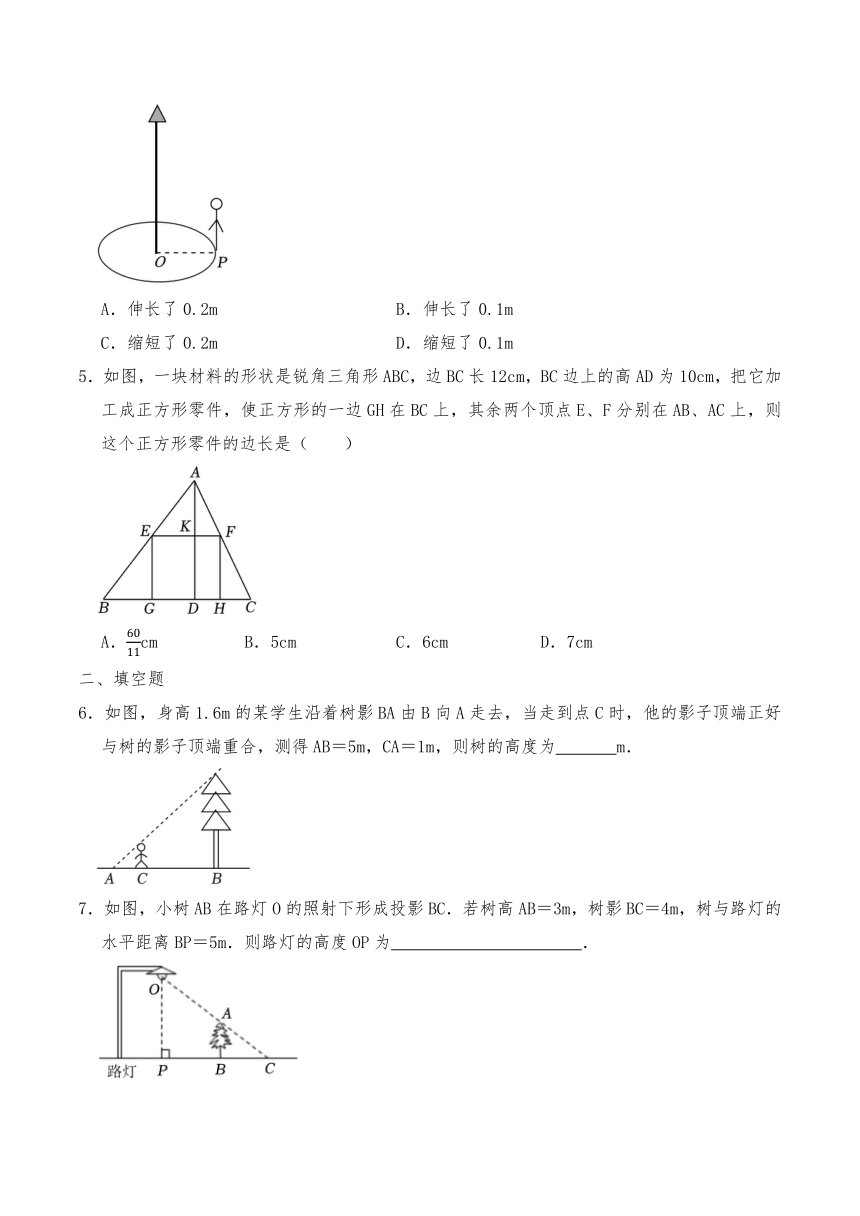
4.如图,广场上有一盏路灯挂在高9.6m的电线杆顶上,记电线杆的底部为O,把路灯看成一个点光源,身高1.6m的小明站在点P处,且OP=2m.当小明向路灯移动0.5m时,影长的变化是( )
A.伸长了0.2m B.伸长了0.1m
C.缩短了0.2m D.缩短了0.1m
5.如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
二、填空题
6.如图,身高1.6m的某学生沿着树影BA由B向A走去,当走到点C时,他的影子顶端正好与树的影子顶端重合,测得AB=5m,CA=1m,则树的高度为 m.
7.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=3m,树影BC=4m,树与路灯的水平距离BP=5m.则路灯的高度OP为 .
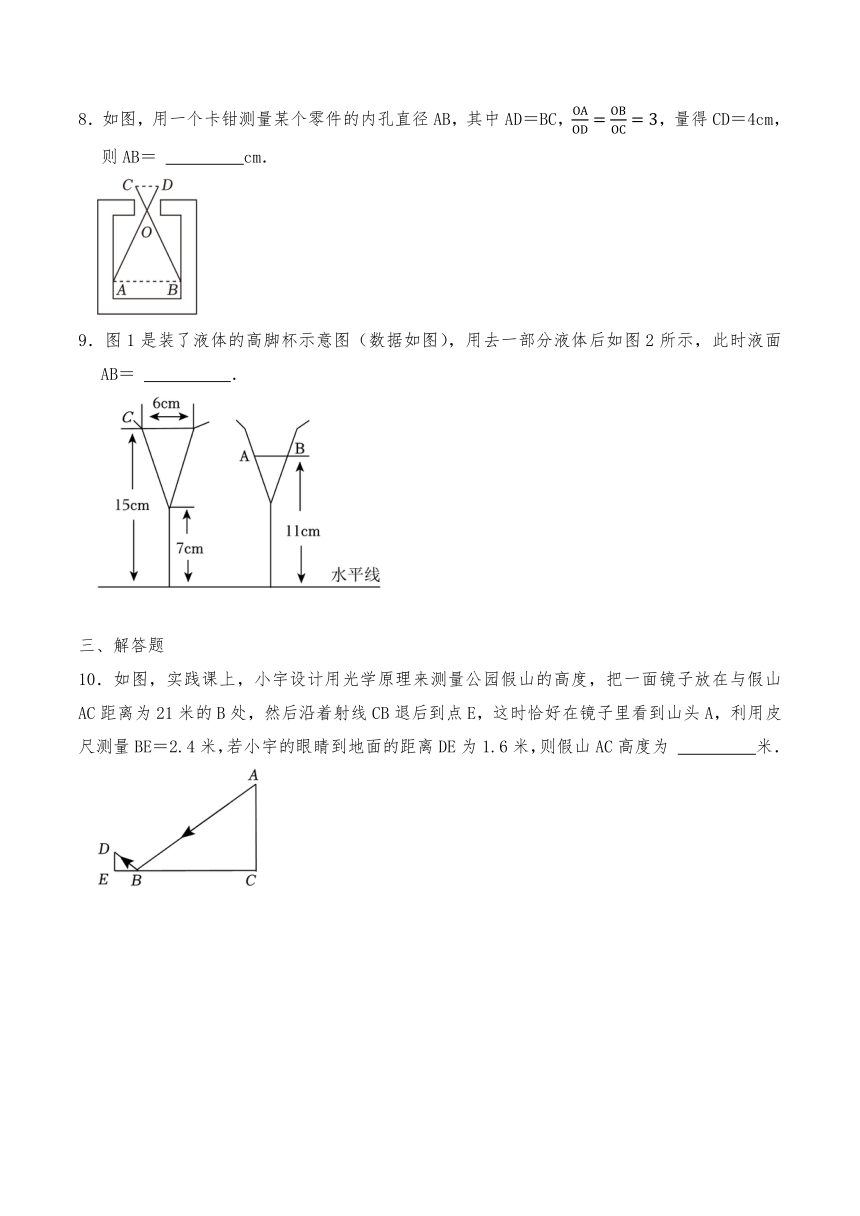
8.如图,用一个卡钳测量某个零件的内孔直径AB,其中AD=BC,,量得CD=4cm,则AB= cm.
9.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB= .
三、解答题
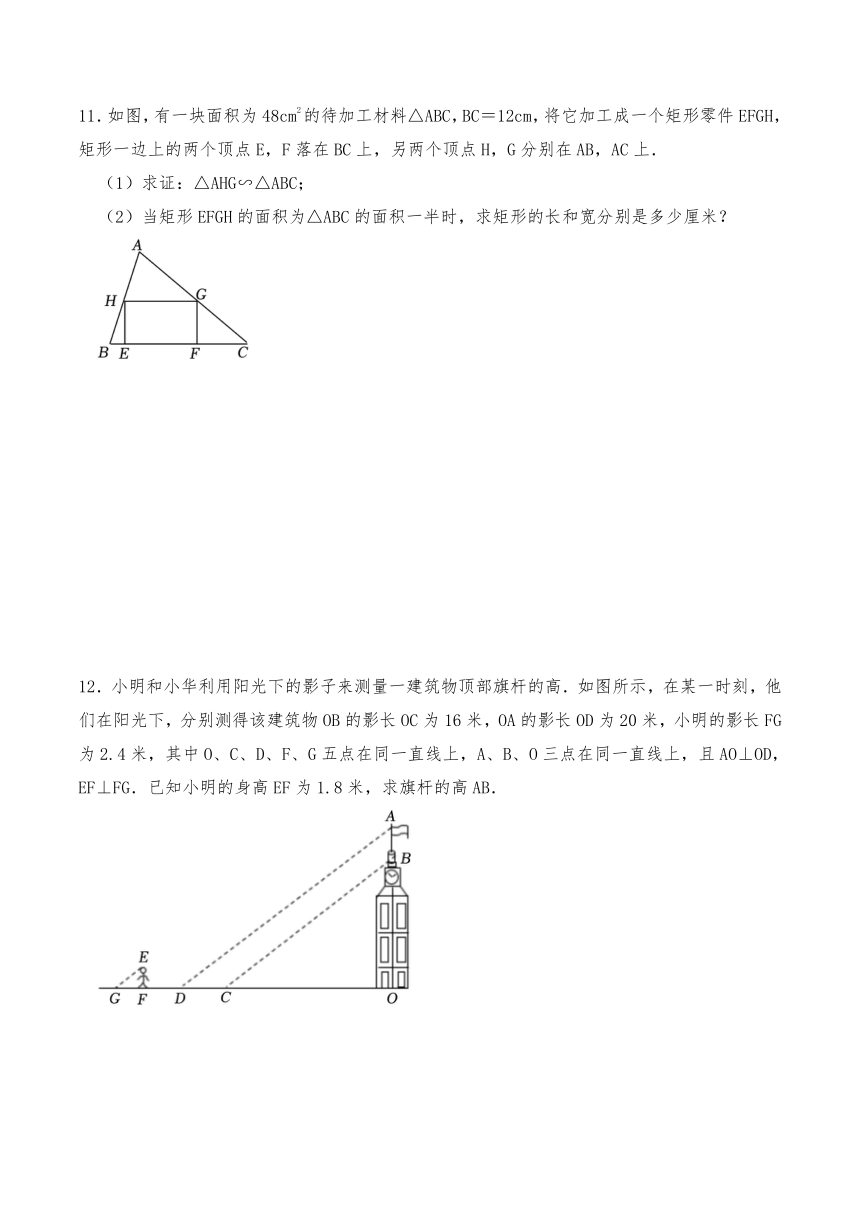
10.如图,实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.4米,若小宇的眼睛到地面的距离DE为1.6米,则假山AC高度为 米.
11.如图,有一块面积为48cm2的待加工材料△ABC,BC=12cm,将它加工成一个矩形零件EFGH,矩形一边上的两个顶点E,F落在BC上,另两个顶点H,G分别在AB,AC上.
(1)求证:△AHG∽△ABC;
(2)当矩形EFGH的面积为△ABC的面积一半时,求矩形的长和宽分别是多少厘米?
12.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
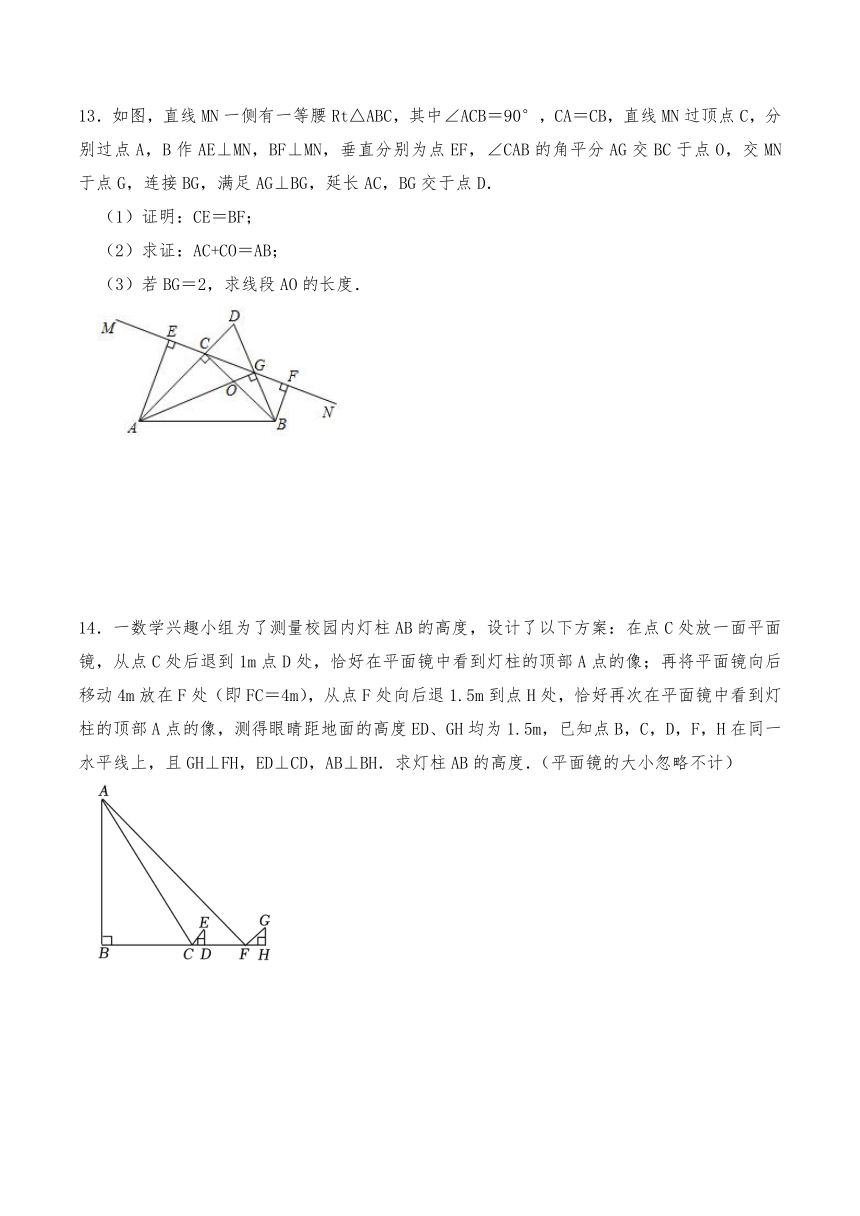
13.如图,直线MN一侧有一等腰Rt△ABC,其中∠ACB=90°,CA=CB,直线MN过顶点C,分别过点A,B作AE⊥MN,BF⊥MN,垂直分别为点EF,∠CAB的角平分AG交BC于点O,交MN于点G,连接BG,满足AG⊥BG,延长AC,BG交于点D.
(1)证明:CE=BF;
(2)求证:AC+CO=AB;
(3)若BG=2,求线段AO的长度.
14.一数学兴趣小组为了测量校园内灯柱AB的高度,设计了以下方案:在点C处放一面平面镜,从点C处后退到1m点D处,恰好在平面镜中看到灯柱的顶部A点的像;再将平面镜向后移动4m放在F处(即FC=4m),从点F处向后退1.5m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,测得眼睛距地面的高度ED、GH均为1.5m,已知点B,C,D,F,H在同一水平线上,且GH⊥FH,ED⊥CD,AB⊥BH.求灯柱AB的高度.(平面镜的大小忽略不计)
15.已知正方形ABCD,E为对角线BD上一点.
(1)如图1,连接AE,CE,求证:△ABE≌△CBE;
(2)如图2,F是CE延长线上一点,CF交AB于点G,AF⊥AE.判断△FAG的形状并说明理由;
(3)在第(2)的条件下,AE=AF=4,求的值.
16.如图1, ABCD的对角线AC与BD交于点O,点E,F分别在边AD,BC上,且AE=CF.点G,H分别是BD与AF,CE的交点.
(1)求证:OG=OH;
(2)连接BE交AC于点P,连接PG,PH.
①如图2,若PG∥AB,求证:PH∥AD;
②如图3,若 ABCD为菱形,且DE=3AE,∠GPH=60°,求的值.
17.如图,正方形EFGH的四个顶点在△ABC的三边上.
(1)如图1,AD为△ABC的高,交EF于点N,若BC=60,AD=40.设EF的长为x.
①直接写出AN的长(用含x的式子表示);
②求正方形EFGH的边长.
(2)如图2,若∠BAC=90°,连接AH交EF于点P,连接AG交EF于点Q.
①求证:EH2=BH CG;
②直接写出EP,PQ,FQ之间的数量关系.
18.如图①,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B运动,运动时间为t秒,连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)求出△BPQ是轴对称图形时t的值;
(3)如图②,连接AQ、CP,若AQ垂直CP,直接写出t的值.
19.如图,在平面直角坐标系中,已知、、三点的坐标为、、,点是线段的一动点,它以每秒2个单位速度从点向点运动,连接过点作的垂线交于点,设点的运动时间为秒.
(1)当点到达的中点时, ;
(2)请用的代数式表示的长度,并求出为何值时,有最小值,是多少?
(3)若已知点在直线上,,为轴上一点且于点,请直接写出满足此条件的点坐标.
20.如图1,为内一点,连接,,如果与相似,那么称点为的“黄金点”.
(1)①等边三角形 “黄金点”(填“存在”或“不存在” ;
②中,,,若点是的“黄金点”,则 ;
(2)如图2,中,,,的中线、交于点,试说明:点是的“黄金点”;
(3)如图3,中,,,,若点是的“黄金点”,且点在的平分线上,求的长.
参考答案
一、单选题
1.
【分析】根据相似三角形的性质列出比例式,把已知数据代入计算即可.
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵BC=3cm,DE=1cm
∴,
解得:AD,
故选:C.
2.
【分析】证明△ABP∽△CDP,推出可得结论.
【解答】解:∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∵∠APB=∠CPD,
∴△ABP∽△CDP,
∴,
∴,
∴CD=13.5m,
故选:D.
3.
【分析】“相似三角形对应高线的比等于相似比”,据此即可求解.
【解答】解:已知物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,设蜡烛火焰的高度是x cm,
由相似三角形的性质得,
解得,
即蜡烛火焰的高度是,
故选:A.
4.
【分析】由题意可得AO∥CP,即得△BPC∽△BOA,得到,求出变化前后BP的长度即可判断求解.
【解答】解:如图,由题意可知,AO∥CP,
∴△BPC∽△BOA,
∴,
∴,
∴BP=0.4m,
当小明向路灯移动0.5m时,BO=2﹣0.5+BP=1.5+BP,
由得:,
∴BP=0.3m,
∴影长缩短了0.4﹣0.3=0.1(m),
故选:D.
5.
【分析】证明△AEF∽△ABC,则,设正方形零件EFHG的边长为x,则AK=10﹣x,根据相似三角形的性质得到,解方程即可.
【解答】解:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
又∵AD⊥BC,
∴,
设正方形零件EFHG的边长为x cm,则AK=(10﹣x)cm,
∴,
解得:,
即这个正方形零件的边长为.
故选:A.
二、填空题
6.
【分析】如图,利用相似三角形的判定与性质证明△ACD∽△ABE即可求解.
【解答】解:当走到点C时,他的影子顶端正好与树的影子顶端重合,标记D,E如图所示,
∵∠ACD=∠ABE=90°,∠DAC=∠EAB,
∴△ACD∽△ABE,
∴,
∵学生的身高为1.6m,
依题意得:CD=1.6m,
∵AB=5m,CA=1m,
∴,
解得BE=8m,
故答案为:8.
7.
【分析】根据AB∥OP,得到△ABC∽△OPC,得到,代入相关数据即可求解.
【解答】解:∵OP⊥PC,AB⊥PC,
∴AB∥OP,
∴△ABC∽△OPC,
∴,
∵AB=3,BC=4,BP=5,
∴PC=BP+BC=9,
∴:
∴,
∴路灯的高度OP为.
故答案为:.
8.
【分析】根据相似三角形的判定和性质,可以求得AB的长.
【解答】解:∵AD,BC相交于O,
∴∠COD=∠AOB,
∵,
∴△AOB∽△COD,
∴,
∴,
∴AB=4×3=12(cm),
故答案为:12.
9.
【分析】高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
【解答】解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴,
∵OM=15﹣7=8(cm),ON=11﹣7=4(cm),
∴,
∴AB=3cm,
故答案为:3cm.
10.
【分析】证明△ACB∽△DEB,则,即,计算求解即可.
【解答】解:∵镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,
∴BC=21米,∠ABC=∠DBE,
又∵∠ACB=90°=∠DEB,
∴△ACB∽△DEB,
∴,
∵BE=2.4米,DE=1.6米,
∴,
解得:AC=14,
故答案为:14.
三、解答题
11.(1)证明:∵四边形EFGH是矩形,
∴HG∥EF,
∴△AHG∽△ABC;
(2)过点A作AD⊥BC于点D,AD交HG于点M,如图,
∵△ABC的面积为48cm2,
∴BC AD=48,
∵BC=12cm,
∴AD=8cm.
∵HG∥EF,AD⊥BC,
∴AM⊥HG,
∴HE=MD=GF.
设HG=x cm,HE=y cm,则DM=y cm,
∴AM=AD﹣DM=(8﹣y)cm,
由(1)知:△AHG∽△ABC,
∴,
∴,
∴y.
∵矩形EFGH的面积为△ABC的面积一半,
∴xy=24.
∴x 24.
解得:x1=x2=6,
∴y4,
∴HG=6cm,HE=4cm,
答:矩形的长为6cm,宽为4cm.
12.解:∵AD∥EG,
∴∠ADO=∠EGF,
∵∠AOD=∠EFG=90°,
∴△AOD∽△EFG,
∴,
∵EF=1.8米,FG=2.4米,OD=20米,
∴,
∴AO=15米,
同理得△BOC∽△AOD,
∴,即,
∴BO=12米,
∴AB=AO﹣BO=15﹣12=3(米),
∴旗杆的高AB是3米.
13.(1)证明:∵AE⊥MN,BF⊥MN,∠ACB=90°
∴∠AEC=∠CFB=∠ABC=90°,
∴∠EAC+∠ACE=90°,∠ACE+∠BCF=90°,
∴∠EAC=∠BCF,
∵AC=BC,
∴△AEC≌△CFB(AAS),
∴CE=BF.
(2)证明:如图1中,作OK⊥AB于K.
∵AC=BC,∠ACB=90°,
∴∠CBA=45°,
∵OK⊥AB,
∴∠OKB=90°,
∴∠KOB=∠KBO=45°,
∴OK=BK,
∵∠OAC=∠OAK,∠ACO=∠AKO=90°,
∵AO=AO,
∴△ACO≌△AKO(AAS),
∴AC=AK,CO=OK,
∴OC=OK=BK,
∴AB=AK+BK=AC+CO.
(3)解:如图2中,在GA上取一点L,使得GL=GB,连接BL.
∵GL=GB=2,
∴BL=2,∠GBL=∠GLB=45°,
∵∠LAB∠DAB=22.5°,∠GLB=∠LAB+∠LBA,
∴∠LAB=∠LBA=22.5°,
∴AL=BL=2,
∴AG=2+2,
在GB上取一点T,使得GO=GT,连接OT,设GO=GT=x.
∵∠TOB=∠TBO=22.5°,
∴OT=BTx,
∴xx=2,
∴x=22,
∴GO=22,
∴AO=AG﹣OG=2+2(22)=4.
解法二:直接证明△ACO≌△CCD,则AO=DB=2BG=4.
14.解:∵∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC.
∴.
∵ED=1.5m,CD=1m,
∴.
设BC=x m,则AB=1.5x m,
同理可得△ABF∽△GHF,
∴.
∵AB=1.5x m,BF=BC+CF=(4+x)m,GH=1.5m,FH=1.5m,
∴,
解得x=8,
∴AB=1.5x=12(m).
答:灯柱AB的高度为12m.
15.(1)证明:∵四边形ABCD为正方形,
∴AB=CB,∠ABE=∠CBE=45°,
∵BE=BE,
∴△ABE≌△CBE(SAS);
(2)解:△FAG为等腰三角形,理由如下:
∵AF⊥AE,
∴∠FAG+∠EAG=90°,
由(1)知∠BCE=∠BAE,
∵∠BCG+∠BGC=90°,
∴∠BGC=∠FAG,
∵∠BGC=∠AGF,
∴∠FAG=∠AGF,
∴FG=AF,
即△FAG为等腰三角形.
(3)解:∵AE=AF=4,
∴∠F=∠AEF=45°,EFAE=4,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴∠AEG=∠ABE,
∵∠GAE=∠BAE,
∴△GAE∽△EAB,
∴,
∴AB AG=16,
由(2)知,AF=FG=4,
∴EG=EF﹣FG=44,
∴∠AGF=∠BGE,
∵∠F=∠GBE,
∴△AFG∽△EBG,
∴,
∴AG BE=AF EG=1616,
∴.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∵AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∴∠AGO=∠CHO,∠OAG=∠OCH,
∴△AOG≌△COH(AAS),
∴OG=OH;
(2)①证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵PG∥AB,
∴,
由(1)知:OG=OH,
∴,
∵∠AOD=∠POH,
∴△AOD∽△POH,
∴∠OAD=∠OPH,
∴PH∥AD;
②解:∵四边形ABCD是菱形,
∴AC⊥BD,AD∥BC,BC=AD,OA=OC,OD=OB,
∴△DEH∽△BCH,△AEP∽△CBP,
∴,,
∵DE=2AE,
∴BC=AD=4AE,
∴,,
∴AP=OP,
设DH=BG=3a,则BH=4a,
∴AD=BH+DH=7a,
∴由(1)知:OG=OH=a,
∴PG=PH,
∵∠GPH=60°,
∴△PGH是等边三角形,
∴AP=OPOH,
∴AC=2OA=4,
∴.
17.(1)解:①∵四边形EFGH是正方形,
∴HE∥DN,∠ENH=∠DHE=90°,HE=EF=x,
∵AD为△ABC的高,
∴AD⊥BC,
∴∠ADH=90°,
∴四边形ENDH为矩形,
∴EH=DN,
∴DN=EF=x,
∴AN=40﹣x;
②∵AD是△ABC的高,
∴∠ADC=90°,
∵四边形EFGH是正方形,
∴EF∥HG,
∴∠ANF=∠ADC=90°,
∵EF∥HG,
∴△AEF∽△ABC,
∴,
∴,
解得:x=24,
答:正方形的边长为24.
(2)①证明:∵正方形EFGH,
∴∠EHG=∠FGH=90°,EH=FG,
∴∠EHB=∠FGC=90°,
∴∠B+∠BEH=90°,
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠BEH=∠C,
∴△BEH∽△FCG,
∴,
∴EH FG=BH CG,
∵EH=FG,
∴EH2=BH CG;
②解:PQ2=EP FQ.
理由:∵EP∥BH,
∴△AEP∽△ABH,
∴,
同理,,
∴,
∴,
∵GH2=EH2=BH CG,
∴PQ2=EP FQ.
18.解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB10(cm);
分两种情况讨论:
当△BPQ∽△BAC时,,
∵BP=5t cm,QC=4t cm,AB=10cm,BC=8cm,
∴,
解得,t=1;
②当△BPO∽△BCA时,,
∴,
解得,;
∴△BPQ与△ABC相似时,t=1或;
(2)∵△BPQ是轴对称图形,
∴△BPQ是等腰三角形,
①当PB=PQ时,如图①﹣1,过P作PH⊥BQ,
则BHBQ=(4﹣2t)cm,PB=5t cm,
∵PH⊥BQ,AC⊥BC,
∴PH∥AC,
∴,即,
解得:;
②当PB=BQ时,即5t=8﹣4t,
解得:;
③当BQ=PQ时,如图②﹣2,过Q作QG⊥AB于G,
则BGPBt cm,BQ=(8﹣4t)cm,
∵∠QBG=∠ABC,∠BGQ=∠BCA=90°,
∴△BGQ∽△BCA,
∴即,
解得:;
综上所述:△BPQ是轴对称图形时t的值为:或或;
(3)过P作PM⊥BC于点M,AQ,CP交于点N,如图②:
则PB=5t cm,PM=3t cm,MC=(8﹣4t)cm,
∵AQ⊥CP,
∴∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,
解得,
∴满足条件的t的值为.
19.解:(1)、、三点的坐标为、、,
,
四边形是菱形,
又,
四边形是正方形,
,
又,
,
,
,
,
为的中点,
,
,
解得:,
.
故答案为:;
(2),
,
,
,
,
时,的值最小,最小值为6;
(3)设,则.
如图,当点在线段上时,
,,
,,
,,
,
,
,
,
解得,
.
当点在的延长线上时,,,
,,
,
,
,
,
或,
,或,.
综上所述,满足条件的点的坐标为或,或,.
20.(1)解:①点是为等边内一点,
是等边三角形,
,
点是为等边内一点,
,,
即,,
不可能是等边三角形,
与一定不相似,
等边三角形不存在“黄金点”,
故答案为:不存在;
②在中,,,
,
若,
则,,
此种情况不存在;
若,
则,,
即点在上,
与为内一矛盾,
此种情况不存在;
若,
则,,,
此种情况成立;
综上可知,,
故答案为:80;
(2)证明:连接,如图2,
在中,,,
设,
,
的中线、交于点,
,是的中位线,,
,,,
,
,,
,
是直角三角形,,
,
点是的“黄金点”;
(3)解:若点是的“黄金点”,由(1)中②可知,则,
,
点在的平分线上,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
.
即的长为.
一、单选题
1.如图,在△ABC中,∠ABC=90°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1.5cm,则AD的长为( )
A. B. C. D.
2.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=6m,BP=8m,PD=18m,那么该古城墙CD的高度是( )m.
A.12 B.10 C.13.5或24 D.13.5
3.《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
4.如图,广场上有一盏路灯挂在高9.6m的电线杆顶上,记电线杆的底部为O,把路灯看成一个点光源,身高1.6m的小明站在点P处,且OP=2m.当小明向路灯移动0.5m时,影长的变化是( )
A.伸长了0.2m B.伸长了0.1m
C.缩短了0.2m D.缩短了0.1m
5.如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
二、填空题
6.如图,身高1.6m的某学生沿着树影BA由B向A走去,当走到点C时,他的影子顶端正好与树的影子顶端重合,测得AB=5m,CA=1m,则树的高度为 m.
7.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=3m,树影BC=4m,树与路灯的水平距离BP=5m.则路灯的高度OP为 .
8.如图,用一个卡钳测量某个零件的内孔直径AB,其中AD=BC,,量得CD=4cm,则AB= cm.
9.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB= .
三、解答题
10.如图,实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.4米,若小宇的眼睛到地面的距离DE为1.6米,则假山AC高度为 米.
11.如图,有一块面积为48cm2的待加工材料△ABC,BC=12cm,将它加工成一个矩形零件EFGH,矩形一边上的两个顶点E,F落在BC上,另两个顶点H,G分别在AB,AC上.
(1)求证:△AHG∽△ABC;
(2)当矩形EFGH的面积为△ABC的面积一半时,求矩形的长和宽分别是多少厘米?
12.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
13.如图,直线MN一侧有一等腰Rt△ABC,其中∠ACB=90°,CA=CB,直线MN过顶点C,分别过点A,B作AE⊥MN,BF⊥MN,垂直分别为点EF,∠CAB的角平分AG交BC于点O,交MN于点G,连接BG,满足AG⊥BG,延长AC,BG交于点D.
(1)证明:CE=BF;
(2)求证:AC+CO=AB;
(3)若BG=2,求线段AO的长度.
14.一数学兴趣小组为了测量校园内灯柱AB的高度,设计了以下方案:在点C处放一面平面镜,从点C处后退到1m点D处,恰好在平面镜中看到灯柱的顶部A点的像;再将平面镜向后移动4m放在F处(即FC=4m),从点F处向后退1.5m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,测得眼睛距地面的高度ED、GH均为1.5m,已知点B,C,D,F,H在同一水平线上,且GH⊥FH,ED⊥CD,AB⊥BH.求灯柱AB的高度.(平面镜的大小忽略不计)
15.已知正方形ABCD,E为对角线BD上一点.
(1)如图1,连接AE,CE,求证:△ABE≌△CBE;
(2)如图2,F是CE延长线上一点,CF交AB于点G,AF⊥AE.判断△FAG的形状并说明理由;
(3)在第(2)的条件下,AE=AF=4,求的值.
16.如图1, ABCD的对角线AC与BD交于点O,点E,F分别在边AD,BC上,且AE=CF.点G,H分别是BD与AF,CE的交点.
(1)求证:OG=OH;
(2)连接BE交AC于点P,连接PG,PH.
①如图2,若PG∥AB,求证:PH∥AD;
②如图3,若 ABCD为菱形,且DE=3AE,∠GPH=60°,求的值.
17.如图,正方形EFGH的四个顶点在△ABC的三边上.
(1)如图1,AD为△ABC的高,交EF于点N,若BC=60,AD=40.设EF的长为x.
①直接写出AN的长(用含x的式子表示);
②求正方形EFGH的边长.
(2)如图2,若∠BAC=90°,连接AH交EF于点P,连接AG交EF于点Q.
①求证:EH2=BH CG;
②直接写出EP,PQ,FQ之间的数量关系.
18.如图①,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B运动,运动时间为t秒,连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)求出△BPQ是轴对称图形时t的值;
(3)如图②,连接AQ、CP,若AQ垂直CP,直接写出t的值.
19.如图,在平面直角坐标系中,已知、、三点的坐标为、、,点是线段的一动点,它以每秒2个单位速度从点向点运动,连接过点作的垂线交于点,设点的运动时间为秒.
(1)当点到达的中点时, ;
(2)请用的代数式表示的长度,并求出为何值时,有最小值,是多少?
(3)若已知点在直线上,,为轴上一点且于点,请直接写出满足此条件的点坐标.
20.如图1,为内一点,连接,,如果与相似,那么称点为的“黄金点”.
(1)①等边三角形 “黄金点”(填“存在”或“不存在” ;
②中,,,若点是的“黄金点”,则 ;
(2)如图2,中,,,的中线、交于点,试说明:点是的“黄金点”;
(3)如图3,中,,,,若点是的“黄金点”,且点在的平分线上,求的长.
参考答案
一、单选题
1.
【分析】根据相似三角形的性质列出比例式,把已知数据代入计算即可.
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵BC=3cm,DE=1cm
∴,
解得:AD,
故选:C.
2.
【分析】证明△ABP∽△CDP,推出可得结论.
【解答】解:∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∵∠APB=∠CPD,
∴△ABP∽△CDP,
∴,
∴,
∴CD=13.5m,
故选:D.
3.
【分析】“相似三角形对应高线的比等于相似比”,据此即可求解.
【解答】解:已知物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,设蜡烛火焰的高度是x cm,
由相似三角形的性质得,
解得,
即蜡烛火焰的高度是,
故选:A.
4.
【分析】由题意可得AO∥CP,即得△BPC∽△BOA,得到,求出变化前后BP的长度即可判断求解.
【解答】解:如图,由题意可知,AO∥CP,
∴△BPC∽△BOA,
∴,
∴,
∴BP=0.4m,
当小明向路灯移动0.5m时,BO=2﹣0.5+BP=1.5+BP,
由得:,
∴BP=0.3m,
∴影长缩短了0.4﹣0.3=0.1(m),
故选:D.
5.
【分析】证明△AEF∽△ABC,则,设正方形零件EFHG的边长为x,则AK=10﹣x,根据相似三角形的性质得到,解方程即可.
【解答】解:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
又∵AD⊥BC,
∴,
设正方形零件EFHG的边长为x cm,则AK=(10﹣x)cm,
∴,
解得:,
即这个正方形零件的边长为.
故选:A.
二、填空题
6.
【分析】如图,利用相似三角形的判定与性质证明△ACD∽△ABE即可求解.
【解答】解:当走到点C时,他的影子顶端正好与树的影子顶端重合,标记D,E如图所示,
∵∠ACD=∠ABE=90°,∠DAC=∠EAB,
∴△ACD∽△ABE,
∴,
∵学生的身高为1.6m,
依题意得:CD=1.6m,
∵AB=5m,CA=1m,
∴,
解得BE=8m,
故答案为:8.
7.
【分析】根据AB∥OP,得到△ABC∽△OPC,得到,代入相关数据即可求解.
【解答】解:∵OP⊥PC,AB⊥PC,
∴AB∥OP,
∴△ABC∽△OPC,
∴,
∵AB=3,BC=4,BP=5,
∴PC=BP+BC=9,
∴:
∴,
∴路灯的高度OP为.
故答案为:.
8.
【分析】根据相似三角形的判定和性质,可以求得AB的长.
【解答】解:∵AD,BC相交于O,
∴∠COD=∠AOB,
∵,
∴△AOB∽△COD,
∴,
∴,
∴AB=4×3=12(cm),
故答案为:12.
9.
【分析】高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
【解答】解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴,
∵OM=15﹣7=8(cm),ON=11﹣7=4(cm),
∴,
∴AB=3cm,
故答案为:3cm.
10.
【分析】证明△ACB∽△DEB,则,即,计算求解即可.
【解答】解:∵镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,
∴BC=21米,∠ABC=∠DBE,
又∵∠ACB=90°=∠DEB,
∴△ACB∽△DEB,
∴,
∵BE=2.4米,DE=1.6米,
∴,
解得:AC=14,
故答案为:14.
三、解答题
11.(1)证明:∵四边形EFGH是矩形,
∴HG∥EF,
∴△AHG∽△ABC;
(2)过点A作AD⊥BC于点D,AD交HG于点M,如图,
∵△ABC的面积为48cm2,
∴BC AD=48,
∵BC=12cm,
∴AD=8cm.
∵HG∥EF,AD⊥BC,
∴AM⊥HG,
∴HE=MD=GF.
设HG=x cm,HE=y cm,则DM=y cm,
∴AM=AD﹣DM=(8﹣y)cm,
由(1)知:△AHG∽△ABC,
∴,
∴,
∴y.
∵矩形EFGH的面积为△ABC的面积一半,
∴xy=24.
∴x 24.
解得:x1=x2=6,
∴y4,
∴HG=6cm,HE=4cm,
答:矩形的长为6cm,宽为4cm.
12.解:∵AD∥EG,
∴∠ADO=∠EGF,
∵∠AOD=∠EFG=90°,
∴△AOD∽△EFG,
∴,
∵EF=1.8米,FG=2.4米,OD=20米,
∴,
∴AO=15米,
同理得△BOC∽△AOD,
∴,即,
∴BO=12米,
∴AB=AO﹣BO=15﹣12=3(米),
∴旗杆的高AB是3米.
13.(1)证明:∵AE⊥MN,BF⊥MN,∠ACB=90°
∴∠AEC=∠CFB=∠ABC=90°,
∴∠EAC+∠ACE=90°,∠ACE+∠BCF=90°,
∴∠EAC=∠BCF,
∵AC=BC,
∴△AEC≌△CFB(AAS),
∴CE=BF.
(2)证明:如图1中,作OK⊥AB于K.
∵AC=BC,∠ACB=90°,
∴∠CBA=45°,
∵OK⊥AB,
∴∠OKB=90°,
∴∠KOB=∠KBO=45°,
∴OK=BK,
∵∠OAC=∠OAK,∠ACO=∠AKO=90°,
∵AO=AO,
∴△ACO≌△AKO(AAS),
∴AC=AK,CO=OK,
∴OC=OK=BK,
∴AB=AK+BK=AC+CO.
(3)解:如图2中,在GA上取一点L,使得GL=GB,连接BL.
∵GL=GB=2,
∴BL=2,∠GBL=∠GLB=45°,
∵∠LAB∠DAB=22.5°,∠GLB=∠LAB+∠LBA,
∴∠LAB=∠LBA=22.5°,
∴AL=BL=2,
∴AG=2+2,
在GB上取一点T,使得GO=GT,连接OT,设GO=GT=x.
∵∠TOB=∠TBO=22.5°,
∴OT=BTx,
∴xx=2,
∴x=22,
∴GO=22,
∴AO=AG﹣OG=2+2(22)=4.
解法二:直接证明△ACO≌△CCD,则AO=DB=2BG=4.
14.解:∵∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC.
∴.
∵ED=1.5m,CD=1m,
∴.
设BC=x m,则AB=1.5x m,
同理可得△ABF∽△GHF,
∴.
∵AB=1.5x m,BF=BC+CF=(4+x)m,GH=1.5m,FH=1.5m,
∴,
解得x=8,
∴AB=1.5x=12(m).
答:灯柱AB的高度为12m.
15.(1)证明:∵四边形ABCD为正方形,
∴AB=CB,∠ABE=∠CBE=45°,
∵BE=BE,
∴△ABE≌△CBE(SAS);
(2)解:△FAG为等腰三角形,理由如下:
∵AF⊥AE,
∴∠FAG+∠EAG=90°,
由(1)知∠BCE=∠BAE,
∵∠BCG+∠BGC=90°,
∴∠BGC=∠FAG,
∵∠BGC=∠AGF,
∴∠FAG=∠AGF,
∴FG=AF,
即△FAG为等腰三角形.
(3)解:∵AE=AF=4,
∴∠F=∠AEF=45°,EFAE=4,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴∠AEG=∠ABE,
∵∠GAE=∠BAE,
∴△GAE∽△EAB,
∴,
∴AB AG=16,
由(2)知,AF=FG=4,
∴EG=EF﹣FG=44,
∴∠AGF=∠BGE,
∵∠F=∠GBE,
∴△AFG∽△EBG,
∴,
∴AG BE=AF EG=1616,
∴.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∵AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∴∠AGO=∠CHO,∠OAG=∠OCH,
∴△AOG≌△COH(AAS),
∴OG=OH;
(2)①证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵PG∥AB,
∴,
由(1)知:OG=OH,
∴,
∵∠AOD=∠POH,
∴△AOD∽△POH,
∴∠OAD=∠OPH,
∴PH∥AD;
②解:∵四边形ABCD是菱形,
∴AC⊥BD,AD∥BC,BC=AD,OA=OC,OD=OB,
∴△DEH∽△BCH,△AEP∽△CBP,
∴,,
∵DE=2AE,
∴BC=AD=4AE,
∴,,
∴AP=OP,
设DH=BG=3a,则BH=4a,
∴AD=BH+DH=7a,
∴由(1)知:OG=OH=a,
∴PG=PH,
∵∠GPH=60°,
∴△PGH是等边三角形,
∴AP=OPOH,
∴AC=2OA=4,
∴.
17.(1)解:①∵四边形EFGH是正方形,
∴HE∥DN,∠ENH=∠DHE=90°,HE=EF=x,
∵AD为△ABC的高,
∴AD⊥BC,
∴∠ADH=90°,
∴四边形ENDH为矩形,
∴EH=DN,
∴DN=EF=x,
∴AN=40﹣x;
②∵AD是△ABC的高,
∴∠ADC=90°,
∵四边形EFGH是正方形,
∴EF∥HG,
∴∠ANF=∠ADC=90°,
∵EF∥HG,
∴△AEF∽△ABC,
∴,
∴,
解得:x=24,
答:正方形的边长为24.
(2)①证明:∵正方形EFGH,
∴∠EHG=∠FGH=90°,EH=FG,
∴∠EHB=∠FGC=90°,
∴∠B+∠BEH=90°,
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠BEH=∠C,
∴△BEH∽△FCG,
∴,
∴EH FG=BH CG,
∵EH=FG,
∴EH2=BH CG;
②解:PQ2=EP FQ.
理由:∵EP∥BH,
∴△AEP∽△ABH,
∴,
同理,,
∴,
∴,
∵GH2=EH2=BH CG,
∴PQ2=EP FQ.
18.解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB10(cm);
分两种情况讨论:
当△BPQ∽△BAC时,,
∵BP=5t cm,QC=4t cm,AB=10cm,BC=8cm,
∴,
解得,t=1;
②当△BPO∽△BCA时,,
∴,
解得,;
∴△BPQ与△ABC相似时,t=1或;
(2)∵△BPQ是轴对称图形,
∴△BPQ是等腰三角形,
①当PB=PQ时,如图①﹣1,过P作PH⊥BQ,
则BHBQ=(4﹣2t)cm,PB=5t cm,
∵PH⊥BQ,AC⊥BC,
∴PH∥AC,
∴,即,
解得:;
②当PB=BQ时,即5t=8﹣4t,
解得:;
③当BQ=PQ时,如图②﹣2,过Q作QG⊥AB于G,
则BGPBt cm,BQ=(8﹣4t)cm,
∵∠QBG=∠ABC,∠BGQ=∠BCA=90°,
∴△BGQ∽△BCA,
∴即,
解得:;
综上所述:△BPQ是轴对称图形时t的值为:或或;
(3)过P作PM⊥BC于点M,AQ,CP交于点N,如图②:
则PB=5t cm,PM=3t cm,MC=(8﹣4t)cm,
∵AQ⊥CP,
∴∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,
解得,
∴满足条件的t的值为.
19.解:(1)、、三点的坐标为、、,
,
四边形是菱形,
又,
四边形是正方形,
,
又,
,
,
,
,
为的中点,
,
,
解得:,
.
故答案为:;
(2),
,
,
,
,
时,的值最小,最小值为6;
(3)设,则.
如图,当点在线段上时,
,,
,,
,,
,
,
,
,
解得,
.
当点在的延长线上时,,,
,,
,
,
,
,
或,
,或,.
综上所述,满足条件的点的坐标为或,或,.
20.(1)解:①点是为等边内一点,
是等边三角形,
,
点是为等边内一点,
,,
即,,
不可能是等边三角形,
与一定不相似,
等边三角形不存在“黄金点”,
故答案为:不存在;
②在中,,,
,
若,
则,,
此种情况不存在;
若,
则,,
即点在上,
与为内一矛盾,
此种情况不存在;
若,
则,,,
此种情况成立;
综上可知,,
故答案为:80;
(2)证明:连接,如图2,
在中,,,
设,
,
的中线、交于点,
,是的中位线,,
,,,
,
,,
,
是直角三角形,,
,
点是的“黄金点”;
(3)解:若点是的“黄金点”,由(1)中②可知,则,
,
点在的平分线上,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
.
即的长为.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
