华师大版七下(2024版)9.3.2旋转的特征学案
文档属性
| 名称 | 华师大版七下(2024版)9.3.2旋转的特征学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9章轴对称、平移与旋转
9.3.2 旋转的特征
学习目标与重难点
学习目标:
1.能结合教材实验,说出旋转的特征:对应点到旋转中心的距离相等、对应角相等、旋转前后图形大小、形状相同;
2.能在简单图形中,根据旋转特征求旋转角度或对应线段长度;
3.通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强 "用数学眼光观察旋转现象" 的意识;
学习重点:理解与应用旋转的特征; 掌握旋转角度的确定方法;
学习难点:旋转性质的综合应用.
预习自测
知识链接
什么是旋转?
旋转由什么决定?
自学自测
1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是 ( )
A.35° B.45° C.55° D.65°
2.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连结AD.下列结论一定正确的是 ( )
A.∠ABD=∠E B.∠CBE+∠DBE<180°
C.AD=BC D.AD∥BC
3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE旋转后得到的图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果连结EF,那么△AEF是怎样的三角形?
教学过程
一、创设情境、导入新课
同学们坐过摩天轮吗?图形的旋转由什么决定的?
二、合作交流、新知探究
探究一: 旋转的特征
教材第141页:
探索1:在图9.3.7中, △AOB 绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处, 你发现有哪些线段相等 有哪些角相等
探索2:在图9.3.8中, △ABC绕点O(点 O 不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处, 你发现有哪些线段相等 有哪些角相等
探究三:例题讲解
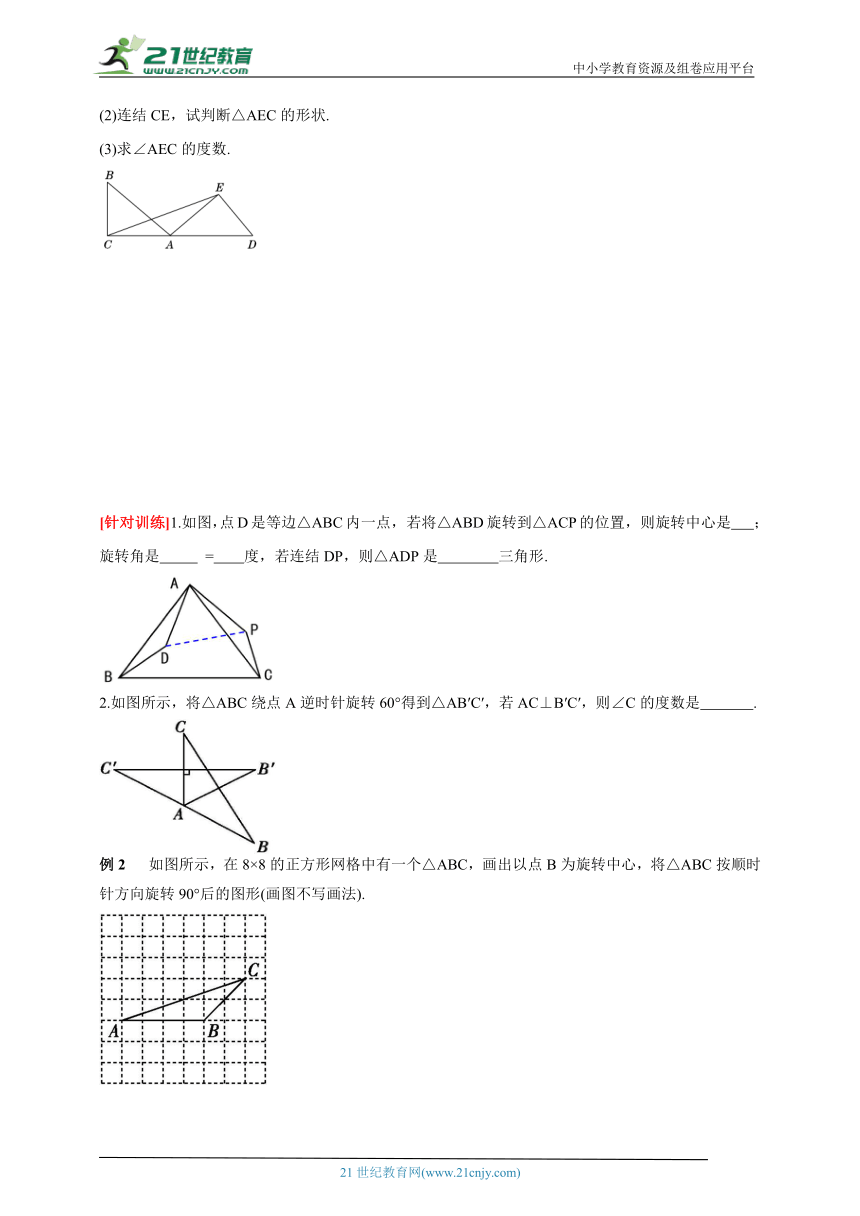
例1 如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
[针对训练]1.如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP的位置, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
2.如图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
例2 如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
[针对训练]3.如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
4.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
做一做:如图,已知△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再作出△A′B′C′关于PR对称的△A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是( )
A.35° B.75° C.55° D.65°
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线,若AB=12,AE=7,则线段CD的长为 .
选做题:
4.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A顺时针旋转30°后得到△AB1C1,求∠BAC1的度数.
5.如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点顺时针旋转α(0°<α<180°),若△AOB绕着O点旋转到图2的位置,若∠BOD=60°,则∠AOC的度数为( )
A.150° B.120° C.60° D.30°
6.如图,△ABC绕点C按顺时针旋转15°得到△DEC,若点A恰好在DE上,则∠BAE的度数为 .
【综合拓展类作业】
7.如图,在△ABC中,∠CAB=100°,将△ABC绕点A按逆时针方向旋转得到△AB'C',点C的对应点为C',点C'恰好在BC边上,且∠C'AB=3∠ABC',则∠ABB'的度数为 .
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
总结反思、拓展升华
【课堂总结】
知识点:1. 旋转三要素:中心、方向、角度
2. 旋转性质:
- 对应点到中心距离相等
- 对应点连线夹角=旋转角
- 对应线段/角相等
- 图形形状,大小完全一样
3. 应用:
- 作图(步骤:定中心→量角度→找对应点)
注意事项:画图时一定要注意旋转中心、旋转方向和旋转角度.
五、【作业布置】
【知识技能类作业】
必做题:
1.如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度数为( )
第1题图
A.65° B.70° C.80° D.85°
2.如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= °.
第2题图
3.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上.若DE⊥AC,∠CAD=25°,则旋转角α的度数是 .
选做题:
4.如图,在6×6的方格中,有一格点三角形ABC(顶点都在小正方形的顶点上)和点P,按下列要求画格点三角形.
(1)画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C';
(2)画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).
5.如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?请你用旋转的性质说明上述关系成立的理由.
【综合拓展类作业】
6.如图,F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 °;
(2)△BEF的形状为 ;
(3)若∠BFC=90°,试说明:AE∥BF.
答案:
自学测试:
1.C 2.D
3.解:(1)旋转中心是A点.
(2)∵△ABF是由△ADE旋转而成的,∴B是D的对应点,
∴∠DAB就是旋转角,即旋转了90°.
(3)∵∠EAF=90°(与旋转角相等)且AF=AE,
∴△AEF是等腰直角三角形.
课堂巩固:
答案:1.D;2.C;3.5;
4. 【解析】因为∠B=45°,∠C=60°,
所以∠BAC=180°-∠B-∠C=75°,
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,所以∠BAC1=75°-30°=45°.
5.B;6.15°;7.64°;
8. 【解析】(1)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=7厘米,CQ=1厘米,AB=3厘米,
所以A'D'=7厘米,C'Q=CQ=1厘米,PD'=1厘米,所以D'Q=2厘米=CP,
所以BP=5厘米,A'P=6厘米,
所以S△A'BP=×BP×A'P=×5×6=15(平方厘米)
(2)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=a厘米,CQ=x厘米,AB=3厘米,
所以A'D'=a厘米,C'Q=CQ=x厘米,PD'=x厘米,所以D'Q=CP=(3-x)厘米,
所以BP=(a+x-3)厘米,A'P=(a-x)厘米,
所以S△A'BP=×BP×A'P=×(a+x-3)×(a-x)= (a2-x2-a+x)平方厘米.
作业布置:
参考答案
1.B 2.90 3.50°
4.(1)如图:
(2)答案不唯一
5.BE=DC.△ABE可以看作△ADC绕点A旋转而成,故这两个三角形的对应线段是相等的.
6.(1)B 90 (2)等腰直角三角形 (3)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第9章轴对称、平移与旋转
9.3.2 旋转的特征
学习目标与重难点
学习目标:
1.能结合教材实验,说出旋转的特征:对应点到旋转中心的距离相等、对应角相等、旋转前后图形大小、形状相同;
2.能在简单图形中,根据旋转特征求旋转角度或对应线段长度;
3.通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强 "用数学眼光观察旋转现象" 的意识;
学习重点:理解与应用旋转的特征; 掌握旋转角度的确定方法;
学习难点:旋转性质的综合应用.
预习自测
知识链接
什么是旋转?
旋转由什么决定?
自学自测
1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是 ( )
A.35° B.45° C.55° D.65°
2.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连结AD.下列结论一定正确的是 ( )
A.∠ABD=∠E B.∠CBE+∠DBE<180°
C.AD=BC D.AD∥BC
3.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE旋转后得到的图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果连结EF,那么△AEF是怎样的三角形?
教学过程
一、创设情境、导入新课
同学们坐过摩天轮吗?图形的旋转由什么决定的?
二、合作交流、新知探究
探究一: 旋转的特征
教材第141页:
探索1:在图9.3.7中, △AOB 绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处, 你发现有哪些线段相等 有哪些角相等
探索2:在图9.3.8中, △ABC绕点O(点 O 不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处, 你发现有哪些线段相等 有哪些角相等
探究三:例题讲解
例1 如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
[针对训练]1.如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP的位置, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
2.如图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
例2 如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
[针对训练]3.如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
4.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
做一做:如图,已知△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再作出△A′B′C′关于PR对称的△A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是( )
A.35° B.75° C.55° D.65°
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线,若AB=12,AE=7,则线段CD的长为 .
选做题:
4.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A顺时针旋转30°后得到△AB1C1,求∠BAC1的度数.
5.如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点顺时针旋转α(0°<α<180°),若△AOB绕着O点旋转到图2的位置,若∠BOD=60°,则∠AOC的度数为( )
A.150° B.120° C.60° D.30°
6.如图,△ABC绕点C按顺时针旋转15°得到△DEC,若点A恰好在DE上,则∠BAE的度数为 .
【综合拓展类作业】
7.如图,在△ABC中,∠CAB=100°,将△ABC绕点A按逆时针方向旋转得到△AB'C',点C的对应点为C',点C'恰好在BC边上,且∠C'AB=3∠ABC',则∠ABB'的度数为 .
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
总结反思、拓展升华
【课堂总结】
知识点:1. 旋转三要素:中心、方向、角度
2. 旋转性质:
- 对应点到中心距离相等
- 对应点连线夹角=旋转角
- 对应线段/角相等
- 图形形状,大小完全一样
3. 应用:
- 作图(步骤:定中心→量角度→找对应点)
注意事项:画图时一定要注意旋转中心、旋转方向和旋转角度.
五、【作业布置】
【知识技能类作业】
必做题:
1.如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度数为( )
第1题图
A.65° B.70° C.80° D.85°
2.如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= °.
第2题图
3.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上.若DE⊥AC,∠CAD=25°,则旋转角α的度数是 .
选做题:
4.如图,在6×6的方格中,有一格点三角形ABC(顶点都在小正方形的顶点上)和点P,按下列要求画格点三角形.
(1)画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C';
(2)画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).
5.如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?请你用旋转的性质说明上述关系成立的理由.
【综合拓展类作业】
6.如图,F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 °;
(2)△BEF的形状为 ;
(3)若∠BFC=90°,试说明:AE∥BF.
答案:
自学测试:
1.C 2.D
3.解:(1)旋转中心是A点.
(2)∵△ABF是由△ADE旋转而成的,∴B是D的对应点,
∴∠DAB就是旋转角,即旋转了90°.
(3)∵∠EAF=90°(与旋转角相等)且AF=AE,
∴△AEF是等腰直角三角形.
课堂巩固:
答案:1.D;2.C;3.5;
4. 【解析】因为∠B=45°,∠C=60°,
所以∠BAC=180°-∠B-∠C=75°,
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,所以∠BAC1=75°-30°=45°.
5.B;6.15°;7.64°;
8. 【解析】(1)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=7厘米,CQ=1厘米,AB=3厘米,
所以A'D'=7厘米,C'Q=CQ=1厘米,PD'=1厘米,所以D'Q=2厘米=CP,
所以BP=5厘米,A'P=6厘米,
所以S△A'BP=×BP×A'P=×5×6=15(平方厘米)
(2)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=a厘米,CQ=x厘米,AB=3厘米,
所以A'D'=a厘米,C'Q=CQ=x厘米,PD'=x厘米,所以D'Q=CP=(3-x)厘米,
所以BP=(a+x-3)厘米,A'P=(a-x)厘米,
所以S△A'BP=×BP×A'P=×(a+x-3)×(a-x)= (a2-x2-a+x)平方厘米.
作业布置:
参考答案
1.B 2.90 3.50°
4.(1)如图:
(2)答案不唯一
5.BE=DC.△ABE可以看作△ADC绕点A旋转而成,故这两个三角形的对应线段是相等的.
6.(1)B 90 (2)等腰直角三角形 (3)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
