华师大版七下(2024版)9.3.2旋转的特征课件
文档属性
| 名称 | 华师大版七下(2024版)9.3.2旋转的特征课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 08:59:27 | ||
图片预览











文档简介
(共32张PPT)
第九章 轴对称、平移与旋转
9.3.2旋转的特征
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能结合教材实验,说出旋转的特征:对应点到旋转中心的距离相等、对应角相等、旋转前后图形大小、形状相同;
01
能在简单图形中,根据旋转特征求旋转角度或对应线段长度;
02
通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
03
通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
04
02
新知导入
思考:同学们坐过摩天轮吗?图形的旋转由什么决定的?
图形的旋转由旋转中心、旋转的角度和旋转的方向所决定。
03
新知探究
在图9.3.7中, △AOB 绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处, 你发现有哪些线段相等 有哪些角相等
如图9.3.7,在旋转过程中, 图形上的每一点绕着点O转过的角度都相等, 即可得∠AOA′ =∠BOB′.
除此以外, 我们还可以发现:
OA = OA′, OB = OB′, AB = A′B′;
∠AOB =∠A′OB′, ∠A =∠A′, ∠B =∠B′.
03
新知探究
在图9.3.8中, △ABC绕点O(点 O 不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处, 你发现有哪些线段相等 有哪些角相等
如图 9.3.8, 在旋转过程中, 我们也可以发现类似的结果:
∠AOA′=∠BOB′=∠COC′;
OA=_____,OB=____,OC=____;
AB=____,BC=____,CA=____;
∠CAB=_________,∠ABC=__________,
∠BCA=_________.
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
03
新知探究
图形旋转的基本性质:
(1) 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;
(2) 对应点到旋转中心的距离相等;
(3) 对应线段相等,对应角相等;
(4) 图形的形状和大小不变;
(5) 旋转中心是唯一不动的点.
概括
04
例题讲解
解析:(1) 由图可知,∠BAD是旋转角.
∵∠BAC=40°,点C,A,D共线,
∴∠BAD=140°,
即△ABC旋转了140°.
如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
例1
(2)由旋转的性质可知,AC=AE,
∴△AEC是等腰三角形.
04
例题讲解
如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
例1
(3)由旋转的性质可知,∠CAE=∠BAD=140°.
又∵AC=AE,
∴∠AEC=(180°-140°)÷2=20°.
04
新知讲解
本题考查的是旋转的性质,理解旋转三要素旋转中心、旋转方向、旋转角度的概念,掌握旋转的性质是解题的关键.
方法总结
2.如图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
1.如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP的位置, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
04
新知探究
点A
∠BAC
60
等边
30°
04
例题讲解
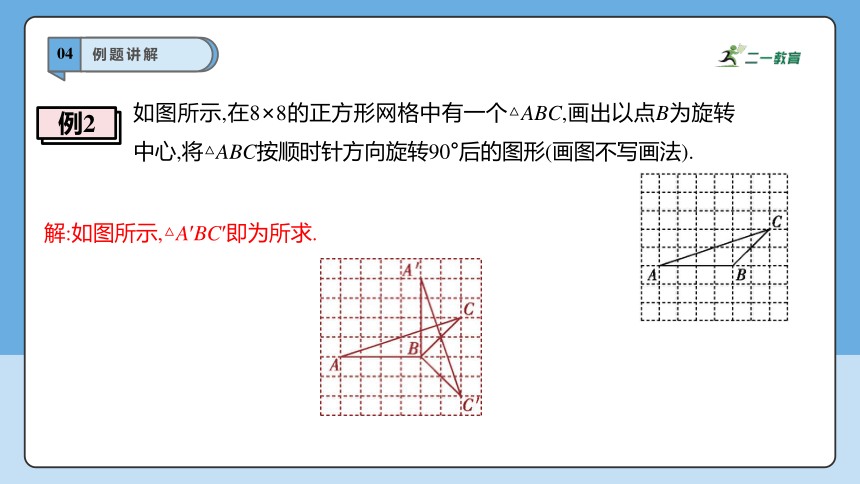
如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
例2
解:如图所示,△A′BC′即为所求.
04
新知讲解
旋转作图的方法:
(1)定中心:先确定图形的关键点;
(2)量角度:利用旋转的特征画出旋转角.
(3)找对应点:利用旋转的特征画出关键点的对应点.
注意:画图时一定要注意旋转中心、旋转方向和旋转角度.
04
新知讲解
3. 如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
04
新知讲解
4.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
解:如图所示,△AB′C′就是所画的图形.
04
新知探究
解:如图,△A″B″C″可以看作是把△ABC绕点P旋转2∠QPR得到的.
如图,已知△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再作出△A′B′C′关于PR对称的△A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
①相同:都是图形的运动;运动前后不改变图形的形状和大小.
②不同:
04
新知探究
[拓展]平移和旋转的异同
1.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是( )
A.35° B.75° C.55° D.65°
05
课堂练习
【知识技能类作业】必做题:
D
C
05
课堂练习
【知识技能类作业】必做题:
5
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线,若AB=12,AE=7,则线段CD的长为 .
05
课堂练习
【知识技能类作业】选做题:
【解析】因为∠B=45°,∠C=60°,
所以∠BAC=180°-∠B-∠C=75°,
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,
所以∠BAC1=75°-30°=45°.
4.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A顺时针旋转30°后得到△AB1C1,求∠BAC1的度数.
05
课堂练习
【知识技能类作业】选做题:
5.如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点顺时针旋转α(0°<α<180°),若△AOB绕着O点旋转到图2的位置,若∠BOD=60°,则∠AOC的度数为( )
A.150° B.120° C.60° D.30°
6.如图,△ABC绕点C按顺时针旋转15°得到△DEC,若点A恰好在DE上,则∠BAE的度数为 .
B
15°
05
课堂练习
【知识技能类作业】选做题:
7.如图,在△ABC中,∠CAB=100°,将△ABC绕点A按逆时针方向旋转得到△AB'C',点C的对应点为C',点C'恰好在BC边上,且∠C'AB=3∠ABC',则∠ABB'的度数为 .
64°
05
课堂练习
【知识技能类作业】选做题:
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
【解析】(1)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=7厘米,CQ=1厘米,AB=3厘米,
所以A'D'=7厘米,C'Q=CQ=1厘米,PD'=1厘米,所以D'Q=2厘米=CP,
所以BP=5厘米,A'P=6厘米,
所以S△A'BP=×BP×A'P=×5×6=15(平方厘米)
05
课堂练习
【知识技能类作业】选做题:
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
(2)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=a厘米,CQ=x厘米,AB=3厘米,
所以A'D'=a厘米,C'Q=CQ=x厘米,PD'=x厘米,所以D'Q=CP=(3-x)厘米,
所以BP=(a+x-3)厘米,A'P=(a-x)厘米,
所以S△A'BP=×BP×A'P=×(a+x-3)×(a-x)= (a2-x2-a+x)平方厘米.
05
课堂小结
旋转的特征
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等, 对应线段相等, 对应角相等, 图形的形状和大小不变.
旋转性质
步骤:定中心→量角度→找对应点
旋转作图
1.如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度数为( )
A.65° B.70° C.80° D.85°
06
作业布置
【知识技能类作业】必做题:
B
2.如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= °.
90
3.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上.若DE⊥AC,∠CAD=25°,则旋转角α的度数是 .
06
作业布置
【知识技能类作业】必做题:
50°
06
作业布置
【知识技能类作业】选做题:
4.如图,在6×6的方格中,有一格点三角形ABC(顶点都在小正方形的顶点上)和点P,按下列要求画格点三角形.
(1)画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C';
(2)画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).
解:(1)如图
解:(2)如图
06
作业布置
【知识技能类作业】选做题:
5.如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?请你用旋转的性质说明上述关系成立的理由.
解:BE=DC.
因为△ABE可以看作△ADC绕点A旋转而成,
故这两个三角形的对应线段是相等的.
06
作业布置
【综合拓展类作业】
(3)∵△BEA绕点B逆时针旋转90°得到△BFC;
∴∠AEB=∠BFC=90°,∠EBF=90°;
∴AE//BF.
6.如图,F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 °;
(2)△BEF的形状为 ;
(3)若∠BFC=90°,试说明:AE∥BF.
B
90
等腰直角三角形
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第九章 轴对称、平移与旋转
9.3.2旋转的特征
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能结合教材实验,说出旋转的特征:对应点到旋转中心的距离相等、对应角相等、旋转前后图形大小、形状相同;
01
能在简单图形中,根据旋转特征求旋转角度或对应线段长度;
02
通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
03
通过 "实验操作→观察猜想→推理论证" 的探究过程,经历从直观到抽象的性质发现,发展几何直观与推理意识;
04
02
新知导入
思考:同学们坐过摩天轮吗?图形的旋转由什么决定的?
图形的旋转由旋转中心、旋转的角度和旋转的方向所决定。
03
新知探究
在图9.3.7中, △AOB 绕点O(点O是三角形的顶点)逆时针旋转到△A′OB′处, 你发现有哪些线段相等 有哪些角相等
如图9.3.7,在旋转过程中, 图形上的每一点绕着点O转过的角度都相等, 即可得∠AOA′ =∠BOB′.
除此以外, 我们还可以发现:
OA = OA′, OB = OB′, AB = A′B′;
∠AOB =∠A′OB′, ∠A =∠A′, ∠B =∠B′.
03
新知探究
在图9.3.8中, △ABC绕点O(点 O 不是三角形的顶点,而是在三角形外)逆时针旋转到△A′B′C′处, 你发现有哪些线段相等 有哪些角相等
如图 9.3.8, 在旋转过程中, 我们也可以发现类似的结果:
∠AOA′=∠BOB′=∠COC′;
OA=_____,OB=____,OC=____;
AB=____,BC=____,CA=____;
∠CAB=_________,∠ABC=__________,
∠BCA=_________.
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
03
新知探究
图形旋转的基本性质:
(1) 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;
(2) 对应点到旋转中心的距离相等;
(3) 对应线段相等,对应角相等;
(4) 图形的形状和大小不变;
(5) 旋转中心是唯一不动的点.
概括
04
例题讲解
解析:(1) 由图可知,∠BAD是旋转角.
∵∠BAC=40°,点C,A,D共线,
∴∠BAD=140°,
即△ABC旋转了140°.
如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
例1
(2)由旋转的性质可知,AC=AE,
∴△AEC是等腰三角形.
04
例题讲解
如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了多少度?
(2)连结CE,试判断△AEC的形状.
(3)求∠AEC的度数.
例1
(3)由旋转的性质可知,∠CAE=∠BAD=140°.
又∵AC=AE,
∴∠AEC=(180°-140°)÷2=20°.
04
新知讲解
本题考查的是旋转的性质,理解旋转三要素旋转中心、旋转方向、旋转角度的概念,掌握旋转的性质是解题的关键.
方法总结
2.如图所示,将△ABC绕点A逆时针旋转60°得到△AB′C′,若AC⊥B′C′,则∠C的度数是 .
1.如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP的位置, 则旋转中心是 ; 旋转角是 = 度,若连结DP,则△ADP是 三角形.
04
新知探究
点A
∠BAC
60
等边
30°
04
例题讲解
如图所示,在8×8的正方形网格中有一个△ABC,画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形(画图不写画法).
例2
解:如图所示,△A′BC′即为所求.
04
新知讲解
旋转作图的方法:
(1)定中心:先确定图形的关键点;
(2)量角度:利用旋转的特征画出旋转角.
(3)找对应点:利用旋转的特征画出关键点的对应点.
注意:画图时一定要注意旋转中心、旋转方向和旋转角度.
04
新知讲解
3. 如图所示,在由边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,请画出旋转后得到的△AB′C′.
04
新知讲解
4.如图所示,△ABC是等腰直角三角形,∠ACB=90°,画出将△ABC以点A为旋转中心,逆时针旋转45°后的图形.
解:如图所示,△AB′C′就是所画的图形.
04
新知探究
解:如图,△A″B″C″可以看作是把△ABC绕点P旋转2∠QPR得到的.
如图,已知△ABC和过点P的两条直线PQ、PR. 作出△ABC关于PQ对称的△A′B′C′,再作出△A′B′C′关于PR对称的△A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
①相同:都是图形的运动;运动前后不改变图形的形状和大小.
②不同:
04
新知探究
[拓展]平移和旋转的异同
1.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,把△ABC绕C点顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是( )
A.35° B.75° C.55° D.65°
05
课堂练习
【知识技能类作业】必做题:
D
C
05
课堂练习
【知识技能类作业】必做题:
5
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线,若AB=12,AE=7,则线段CD的长为 .
05
课堂练习
【知识技能类作业】选做题:
【解析】因为∠B=45°,∠C=60°,
所以∠BAC=180°-∠B-∠C=75°,
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,
所以∠BAC1=75°-30°=45°.
4.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A顺时针旋转30°后得到△AB1C1,求∠BAC1的度数.
05
课堂练习
【知识技能类作业】选做题:
5.如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点顺时针旋转α(0°<α<180°),若△AOB绕着O点旋转到图2的位置,若∠BOD=60°,则∠AOC的度数为( )
A.150° B.120° C.60° D.30°
6.如图,△ABC绕点C按顺时针旋转15°得到△DEC,若点A恰好在DE上,则∠BAE的度数为 .
B
15°
05
课堂练习
【知识技能类作业】选做题:
7.如图,在△ABC中,∠CAB=100°,将△ABC绕点A按逆时针方向旋转得到△AB'C',点C的对应点为C',点C'恰好在BC边上,且∠C'AB=3∠ABC',则∠ABB'的度数为 .
64°
05
课堂练习
【知识技能类作业】选做题:
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
【解析】(1)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=7厘米,CQ=1厘米,AB=3厘米,
所以A'D'=7厘米,C'Q=CQ=1厘米,PD'=1厘米,所以D'Q=2厘米=CP,
所以BP=5厘米,A'P=6厘米,
所以S△A'BP=×BP×A'P=×5×6=15(平方厘米)
05
课堂练习
【知识技能类作业】选做题:
8.如图,在长方形ABCD中,AB=3厘米,BC=a厘米(a>3),点Q在边CD上(不与点C,D重合),CQ=x厘米.将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',且重叠部分的四边形PCQD'是长方形.连结A'B,C'D.
(1)若BC=7厘米,CQ=1厘米,求△A'BP的面积;
(2)用含有x,a的代数式表示△A'BP的面积;
(2)因为将长方形ABCD绕点Q顺时针旋转90度后,得到长方形A'B'C'D',
所以QD=QD',CQ=C'Q,A'D'=AD=BC,
因为BC=a厘米,CQ=x厘米,AB=3厘米,
所以A'D'=a厘米,C'Q=CQ=x厘米,PD'=x厘米,所以D'Q=CP=(3-x)厘米,
所以BP=(a+x-3)厘米,A'P=(a-x)厘米,
所以S△A'BP=×BP×A'P=×(a+x-3)×(a-x)= (a2-x2-a+x)平方厘米.
05
课堂小结
旋转的特征
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等, 对应线段相等, 对应角相等, 图形的形状和大小不变.
旋转性质
步骤:定中心→量角度→找对应点
旋转作图
1.如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度数为( )
A.65° B.70° C.80° D.85°
06
作业布置
【知识技能类作业】必做题:
B
2.如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= °.
90
3.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上.若DE⊥AC,∠CAD=25°,则旋转角α的度数是 .
06
作业布置
【知识技能类作业】必做题:
50°
06
作业布置
【知识技能类作业】选做题:
4.如图,在6×6的方格中,有一格点三角形ABC(顶点都在小正方形的顶点上)和点P,按下列要求画格点三角形.
(1)画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C';
(2)画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).
解:(1)如图
解:(2)如图
06
作业布置
【知识技能类作业】选做题:
5.如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?请你用旋转的性质说明上述关系成立的理由.
解:BE=DC.
因为△ABE可以看作△ADC绕点A旋转而成,
故这两个三角形的对应线段是相等的.
06
作业布置
【综合拓展类作业】
(3)∵△BEA绕点B逆时针旋转90°得到△BFC;
∴∠AEB=∠BFC=90°,∠EBF=90°;
∴AE//BF.
6.如图,F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 °;
(2)△BEF的形状为 ;
(3)若∠BFC=90°,试说明:AE∥BF.
B
90
等腰直角三角形
Thanks!
https://www.21cnjy.com/recruitment/home/fine
