华师大版七下(2024版)9.3.3旋转对称图形课件
文档属性
| 名称 | 华师大版七下(2024版)9.3.3旋转对称图形课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 08:59:27 | ||
图片预览










文档简介
(共35张PPT)
第九章 轴对称、平移与旋转
9.3.3旋转对称图形
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
学生能识别旋转对称图形,归纳其定义并描述特征;能找出给定旋转对称图形的旋转中心,计算最小旋转角度,掌握正多边形旋转角度的计算方法;
01
通过观察实例、动手操作、小组合作,经历从具体到抽象的思维过程,培养观察、实践和合作交流能力;在探究性质时运用类比、归纳、推理等方法,提升逻辑思维和数学素养,学会从数学角度分析解决问题;
02
感受旋转对称图形在生活中的应用,体会数学与生活的联系,激发学习兴趣。通过小组合作,培养团队协作和创新意识,体验成功喜悦,增强学习数学的自信心.
03
02
新知导入
复习导入:旋转的特征有哪些?
(1) 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;
(2) 对应点到旋转中心的距离相等;
(3) 对应线段相等,对应角相等;
(4) 图形的形状和大小不变;
(5) 旋转中心是唯一不动的点.
02
新知导入
思考:怎样画一个图形关于一个点旋转后的图形?
主要是画几个点旋转后的点.
如何来确定旋转中心?
用两组对应点连线的中垂线的交点.
03
新知探究
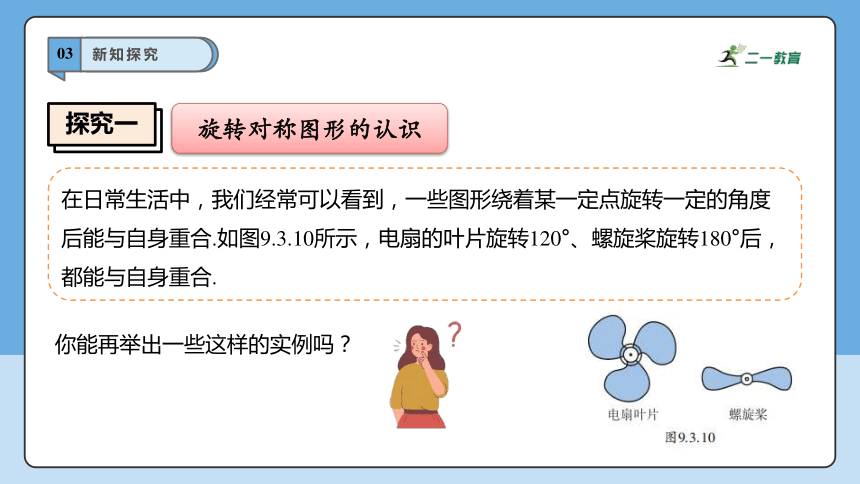
在日常生活中,我们经常可以看到,一些图形绕着某一定点旋转一定的角度后能与自身重合.如图9.3.10所示,电扇的叶片旋转120°、螺旋桨旋转180°后,都能与自身重合.
探究一
旋转对称图形的认识
你能再举出一些这样的实例吗?
02
新知探究
用一张半透明的薄纸,覆盖在如图9.3.11所示的图形上,在薄纸上画这个图形,使它与如图9.3.11所示的图形重合.然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度 (小于周角)后,薄纸上的图形能与原图形再一次重合.
02
新知探究
由上述操作可知:该图形围绕圆心旋转60°、120°、180°、240°、300°后都能与自身重合.
像这样旋转一定角度后能与自身重合的图形就称为旋转对称图形.
概括
02
新知探究
顺时针和逆时针旋转对旋转对称图形有影响吗?
旋转对称图形顺时针或逆时针旋转一定角度后,均能与原图形重合,因此可以淡化旋转方向.旋转角度可以在0°到360°之间.
针对练习:下列图形是旋转对称图形(即绕一个点旋转后能与原图重合的图形)的是( )
02
新知探究
C
03
新知探究
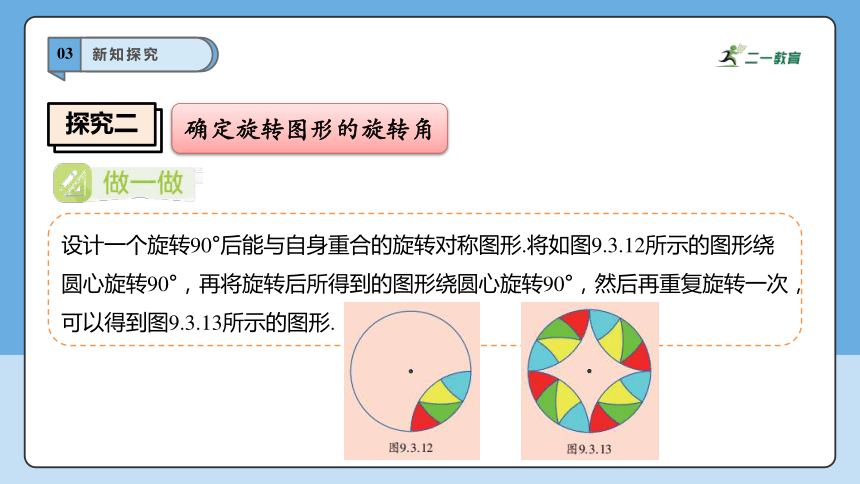
探究二
确定旋转图形的旋转角
设计一个旋转90°后能与自身重合的旋转对称图形.将如图9.3.12所示的图形绕圆心旋转90°,再将旋转后所得到的图形绕圆心旋转90°,然后再重复旋转一次,可以得到图9.3.13所示的图形.
02
新知探究
将如图9.3.13所示的图形绕圆心旋转90°后,可以发现旋转以后的图形能与原来位置上的原图形重合,因此该图形是旋转对称图形.当然该图形绕圆心旋转180或270°后的图形也能与原图形重合,也可得出该图形是旋转对称图形.旋转的度数称为旋转角度.
02
新知探究
你能设计一个旋转30°后能与自身重合的图形吗?
02
新知探究
针对练习
以下图形绕点O旋转一定角度后都能与原图形重合,其中旋转角最小的是( )
C
02
新知探究
(1)绕着某一点转动一定角度后能与自身重合的图形称为旋转对称图形.其中这一点就是旋转中心,这个角度就是旋转角度;
(2)如果一个图形既是旋转对称图形,又是轴对称图形,那么它的旋转中心就是对称轴的交点;
(3)正n边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点,并且旋转角度就等于360°除以n所得的商.
概括
02
新知探究
拓展延伸:旋转对称图形与以前学过的轴对称图形相同吗?
1.旋转对称图形与轴对称图形是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
2.一个是旋转一定的角度得到,一个是翻折得到.
03
例题讲解
解析:这个图形是旋转对称图形,旋转中心是外框正方形对角线的交点(如图2中的点),旋转角度是,但它不是轴对称图形.
观察图1,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗?
例1
03
新知讲解
判断旋转对称图形要用定义进行判断;思考图形旋转多少度能与自身完全重合时一般要求出旋转到能与自身重合的最小角度.
方法总结
03
例题讲解
下列各图形是不是旋转对称图形?如果是,请找出旋转中心在何处?旋转角度是多少?这些图形是轴对称图形吗?
例2
解:如图,它们均为旋转对称图形;如图它们的旋转中心在图形中心红点;它们的旋转角分别为:, , , ;它们均为轴对称图形.
1.如图所示的图形中,是旋转对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
04
课堂练习
【知识技能类作业】必做题:
D
2.下列四个图形中,旋转某一个角度都能与自身重合,其中旋转角度最小的是( )
A
3.如图是一个旋转对称图形,以点O为旋转中心,以下列角度为旋转角旋转,能使旋转后的图形与原图形重合的是( )
A.60° B.90° C.120° D.180°
04
课堂练习
【知识技能类作业】必做题:
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,所给图形中是轴对称图形的有________个,是旋转对称图形的有________个.
2
3
5.(1)如图9①所示的图形是________对称图形,它的对称轴有________条;它又是________对称图形,至少旋转________后能与自身重合.
(2)如图9②所示的图形是________对称图形,它的对称轴有________条;它又是________对称图形,至少旋转________后能与自身重合.
轴
4
旋转
轴
2
旋转
04
课堂练习
【知识技能类作业】选做题:
6.如图,点O是正六边形的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O至少旋转多少度后能与自身重合?
(3)如果换成其他的正多边形呢?能得到一般结论吗?
解:(1)直线AD,BE,CF以及AB,BC,CD的垂直平分线都是这个正六边形的对称轴.
(2)60°.
(3)一般地,正n边形每条边的垂直平分线都是其对称轴.当n为偶数时,相对顶点的连线所在的直线也是其对称轴.绕正n边形的中心至少旋转()能与自身重合.
7.认真观察下图所示的四个图中阴影部分构成的图案,回答下列问题:
请写出这四个图案都具有的两个特征.
特征1:________________________________;
特征2:________________________________.
04
课堂练习
都是轴对称图形
【综合拓展类作业】
都是旋转对称图形
04
课堂练习
【知识技能类作业】选做题:
8.如图所示的网格中有四个三角形.
(1)请你把图补充成旋转对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数,这个整体图形至少旋转多少度才能与自身重合?
解:(1)如图.
(2)这个整体图形有4条对称轴,这个整体图形至少旋转90°才能与自身重合.
05
课堂小结
旋转对称图形
像这样旋转一定角度后能与自身重合的图形就称为旋转对称围形。
定义
如果一个图形既是旋转对称图形。又是轴对称图形,那么它的旋转中心就是对称轴的交点。正边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点。井且旋转角度就等于360除于n所得的。
旋转中心与旋转角
1.下列图形中,不属于旋转对称图形的是( )
2.三叶电风扇叶片的外形是一个旋转对称图形,其最小旋转角的度数是( )
A.60° B.120° C.180° D.240°
06
作业布置
【知识技能类作业】必做题:
D
C
3.给出下列图形:①线段;②平行四边形;③圆;④长方形;⑤等边三角形.其中,旋转对称图形是__________(只填序号).
06
作业布置
【知识技能类作业】必做题:
①②③④⑤
4.如图所示的图标可以看作是一个平行四边形通过________次旋转得到的,每次旋转的角度为________.
2
120°
06
作业布置
【知识技能类作业】选做题:
解:这个图形的旋转中心为外圆的圆心.
∵360°÷6=60°,
∴该图形绕旋转中心至少旋转60°才能和原来的图形重合.
5.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来的图形重合?
6.如图所示的图案绕其中心旋转n°时与原图案完全重合,那么n的最小值是( )
A.60 B.90 C.120 D.180
06
作业布置
【知识技能类作业】选做题:
C
06
作业布置
【知识技能类作业】选做题:
7.如图是某设计师设计的方桌布图案的一部分,请运用旋转变换的方法,在方格纸上画出该图形绕点O顺时针依次旋转90°,180°,270°后的图形.整个图案是旋转对称图形吗?(注意:涂阴影时要利用旋转变换的特点,不要涂错了位置)
解:如图所示.
整个图案是旋转对称图形.
06
作业布置
【综合拓展类作业】
8.如图所示,点O是等边三角形ABC的中心,射线OE交AB边于点E,OF交BC边于点F,若△ABC的面积为S,∠EOF=120°,则当∠EOF绕点O旋转时,得到的阴影面积发生变化吗?下面有三名同学提出了各自的观点.
甲:阴影部分的面积会发生变化,且当OE,OF分别与△ABC的边垂直时,阴影部分的面积最小.
乙:阴影部分的面积会发生变化,且当E,F分别与△ABC的顶点重合时,阴影部分的面积最大.
丙:无论怎样旋转,阴影部分的面积都保持不变.
你支持谁的观点?____________.
06
作业布置
【综合拓展类作业】
解:丙
连结绕点逆时针旋转得到,
,
.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第九章 轴对称、平移与旋转
9.3.3旋转对称图形
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
学生能识别旋转对称图形,归纳其定义并描述特征;能找出给定旋转对称图形的旋转中心,计算最小旋转角度,掌握正多边形旋转角度的计算方法;
01
通过观察实例、动手操作、小组合作,经历从具体到抽象的思维过程,培养观察、实践和合作交流能力;在探究性质时运用类比、归纳、推理等方法,提升逻辑思维和数学素养,学会从数学角度分析解决问题;
02
感受旋转对称图形在生活中的应用,体会数学与生活的联系,激发学习兴趣。通过小组合作,培养团队协作和创新意识,体验成功喜悦,增强学习数学的自信心.
03
02
新知导入
复习导入:旋转的特征有哪些?
(1) 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;
(2) 对应点到旋转中心的距离相等;
(3) 对应线段相等,对应角相等;
(4) 图形的形状和大小不变;
(5) 旋转中心是唯一不动的点.
02
新知导入
思考:怎样画一个图形关于一个点旋转后的图形?
主要是画几个点旋转后的点.
如何来确定旋转中心?
用两组对应点连线的中垂线的交点.
03
新知探究
在日常生活中,我们经常可以看到,一些图形绕着某一定点旋转一定的角度后能与自身重合.如图9.3.10所示,电扇的叶片旋转120°、螺旋桨旋转180°后,都能与自身重合.
探究一
旋转对称图形的认识
你能再举出一些这样的实例吗?
02
新知探究
用一张半透明的薄纸,覆盖在如图9.3.11所示的图形上,在薄纸上画这个图形,使它与如图9.3.11所示的图形重合.然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度 (小于周角)后,薄纸上的图形能与原图形再一次重合.
02
新知探究
由上述操作可知:该图形围绕圆心旋转60°、120°、180°、240°、300°后都能与自身重合.
像这样旋转一定角度后能与自身重合的图形就称为旋转对称图形.
概括
02
新知探究
顺时针和逆时针旋转对旋转对称图形有影响吗?
旋转对称图形顺时针或逆时针旋转一定角度后,均能与原图形重合,因此可以淡化旋转方向.旋转角度可以在0°到360°之间.
针对练习:下列图形是旋转对称图形(即绕一个点旋转后能与原图重合的图形)的是( )
02
新知探究
C
03
新知探究
探究二
确定旋转图形的旋转角
设计一个旋转90°后能与自身重合的旋转对称图形.将如图9.3.12所示的图形绕圆心旋转90°,再将旋转后所得到的图形绕圆心旋转90°,然后再重复旋转一次,可以得到图9.3.13所示的图形.
02
新知探究
将如图9.3.13所示的图形绕圆心旋转90°后,可以发现旋转以后的图形能与原来位置上的原图形重合,因此该图形是旋转对称图形.当然该图形绕圆心旋转180或270°后的图形也能与原图形重合,也可得出该图形是旋转对称图形.旋转的度数称为旋转角度.
02
新知探究
你能设计一个旋转30°后能与自身重合的图形吗?
02
新知探究
针对练习
以下图形绕点O旋转一定角度后都能与原图形重合,其中旋转角最小的是( )
C
02
新知探究
(1)绕着某一点转动一定角度后能与自身重合的图形称为旋转对称图形.其中这一点就是旋转中心,这个角度就是旋转角度;
(2)如果一个图形既是旋转对称图形,又是轴对称图形,那么它的旋转中心就是对称轴的交点;
(3)正n边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点,并且旋转角度就等于360°除以n所得的商.
概括
02
新知探究
拓展延伸:旋转对称图形与以前学过的轴对称图形相同吗?
1.旋转对称图形与轴对称图形是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
2.一个是旋转一定的角度得到,一个是翻折得到.
03
例题讲解
解析:这个图形是旋转对称图形,旋转中心是外框正方形对角线的交点(如图2中的点),旋转角度是,但它不是轴对称图形.
观察图1,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗?
例1
03
新知讲解
判断旋转对称图形要用定义进行判断;思考图形旋转多少度能与自身完全重合时一般要求出旋转到能与自身重合的最小角度.
方法总结
03
例题讲解
下列各图形是不是旋转对称图形?如果是,请找出旋转中心在何处?旋转角度是多少?这些图形是轴对称图形吗?
例2
解:如图,它们均为旋转对称图形;如图它们的旋转中心在图形中心红点;它们的旋转角分别为:, , , ;它们均为轴对称图形.
1.如图所示的图形中,是旋转对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
04
课堂练习
【知识技能类作业】必做题:
D
2.下列四个图形中,旋转某一个角度都能与自身重合,其中旋转角度最小的是( )
A
3.如图是一个旋转对称图形,以点O为旋转中心,以下列角度为旋转角旋转,能使旋转后的图形与原图形重合的是( )
A.60° B.90° C.120° D.180°
04
课堂练习
【知识技能类作业】必做题:
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,所给图形中是轴对称图形的有________个,是旋转对称图形的有________个.
2
3
5.(1)如图9①所示的图形是________对称图形,它的对称轴有________条;它又是________对称图形,至少旋转________后能与自身重合.
(2)如图9②所示的图形是________对称图形,它的对称轴有________条;它又是________对称图形,至少旋转________后能与自身重合.
轴
4
旋转
轴
2
旋转
04
课堂练习
【知识技能类作业】选做题:
6.如图,点O是正六边形的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O至少旋转多少度后能与自身重合?
(3)如果换成其他的正多边形呢?能得到一般结论吗?
解:(1)直线AD,BE,CF以及AB,BC,CD的垂直平分线都是这个正六边形的对称轴.
(2)60°.
(3)一般地,正n边形每条边的垂直平分线都是其对称轴.当n为偶数时,相对顶点的连线所在的直线也是其对称轴.绕正n边形的中心至少旋转()能与自身重合.
7.认真观察下图所示的四个图中阴影部分构成的图案,回答下列问题:
请写出这四个图案都具有的两个特征.
特征1:________________________________;
特征2:________________________________.
04
课堂练习
都是轴对称图形
【综合拓展类作业】
都是旋转对称图形
04
课堂练习
【知识技能类作业】选做题:
8.如图所示的网格中有四个三角形.
(1)请你把图补充成旋转对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数,这个整体图形至少旋转多少度才能与自身重合?
解:(1)如图.
(2)这个整体图形有4条对称轴,这个整体图形至少旋转90°才能与自身重合.
05
课堂小结
旋转对称图形
像这样旋转一定角度后能与自身重合的图形就称为旋转对称围形。
定义
如果一个图形既是旋转对称图形。又是轴对称图形,那么它的旋转中心就是对称轴的交点。正边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点。井且旋转角度就等于360除于n所得的。
旋转中心与旋转角
1.下列图形中,不属于旋转对称图形的是( )
2.三叶电风扇叶片的外形是一个旋转对称图形,其最小旋转角的度数是( )
A.60° B.120° C.180° D.240°
06
作业布置
【知识技能类作业】必做题:
D
C
3.给出下列图形:①线段;②平行四边形;③圆;④长方形;⑤等边三角形.其中,旋转对称图形是__________(只填序号).
06
作业布置
【知识技能类作业】必做题:
①②③④⑤
4.如图所示的图标可以看作是一个平行四边形通过________次旋转得到的,每次旋转的角度为________.
2
120°
06
作业布置
【知识技能类作业】选做题:
解:这个图形的旋转中心为外圆的圆心.
∵360°÷6=60°,
∴该图形绕旋转中心至少旋转60°才能和原来的图形重合.
5.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来的图形重合?
6.如图所示的图案绕其中心旋转n°时与原图案完全重合,那么n的最小值是( )
A.60 B.90 C.120 D.180
06
作业布置
【知识技能类作业】选做题:
C
06
作业布置
【知识技能类作业】选做题:
7.如图是某设计师设计的方桌布图案的一部分,请运用旋转变换的方法,在方格纸上画出该图形绕点O顺时针依次旋转90°,180°,270°后的图形.整个图案是旋转对称图形吗?(注意:涂阴影时要利用旋转变换的特点,不要涂错了位置)
解:如图所示.
整个图案是旋转对称图形.
06
作业布置
【综合拓展类作业】
8.如图所示,点O是等边三角形ABC的中心,射线OE交AB边于点E,OF交BC边于点F,若△ABC的面积为S,∠EOF=120°,则当∠EOF绕点O旋转时,得到的阴影面积发生变化吗?下面有三名同学提出了各自的观点.
甲:阴影部分的面积会发生变化,且当OE,OF分别与△ABC的边垂直时,阴影部分的面积最小.
乙:阴影部分的面积会发生变化,且当E,F分别与△ABC的顶点重合时,阴影部分的面积最大.
丙:无论怎样旋转,阴影部分的面积都保持不变.
你支持谁的观点?____________.
06
作业布置
【综合拓展类作业】
解:丙
连结绕点逆时针旋转得到,
,
.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
