19.3 课题学习 选择方案 同步试题 2024--2025学年初中数学人教版八年级下册
文档属性
| 名称 | 19.3 课题学习 选择方案 同步试题 2024--2025学年初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 559.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.3 课题学习 选择方案 同步试题
2024--2025学年初中数学人教版八年级下册
一、单选题
1.如图,大长方形的长为x,在左侧截掉一个面积最大的正方形. 若剩余部分的周长是y,则y与x的函数关系式是 ( )
A. B. C. D.
2.一条观光船沿直线向码头前进,下表记录了4个时间点观光船与码头的距离,其中t表示时间,y表示观光船与码头的距离.
0 3 6 9
675 600 525 450
如果观光船保持这样的行进状态继续前进,那么从开始计时到观光船与码头的距离为150m时,所用时间为( )
A.25min B.21min C.13min D.12min
3.暑假里父母带小明外出旅行,了解到东方旅行社规定:若父母各买一张全票,则孩子的 费用可按全票价七折优惠(即优惠30%);而光明旅行社规定:三人旅行可按团体票计价,即按全票价的90%收费,若已知旅行社的全票价相同,则实际收费( )
A.东方旅行社比光明旅行社低
B.东方旅行社与光明旅行社相同
C.东方旅行社比光明旅行社高
D.谁高谁低视全票价多少而定
4.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
5.某商场在促销活动中,计划销售型和型两种饮水机共20台.若每台型饮水机可盈利150元,每台型饮水机可盈利200元,型饮水机的销售量不小于型饮水机的3倍.则该商场在本次促销活动中销售这两种饮水机能获得的最大利润是( )
A.3400元 B.3250元 C.4600元 D.4750元
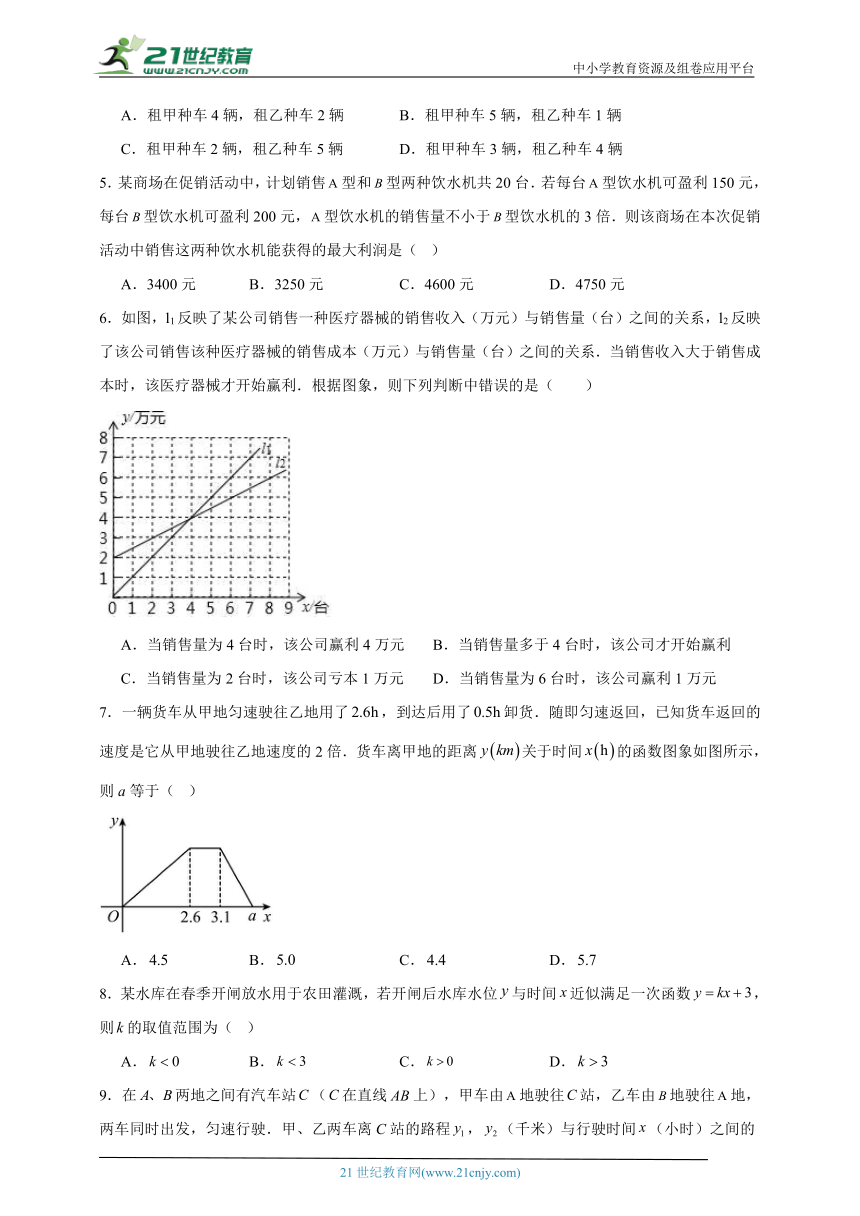
6.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
A.当销售量为4台时,该公司赢利4万元 B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元 D.当销售量为6台时,该公司赢利1万元
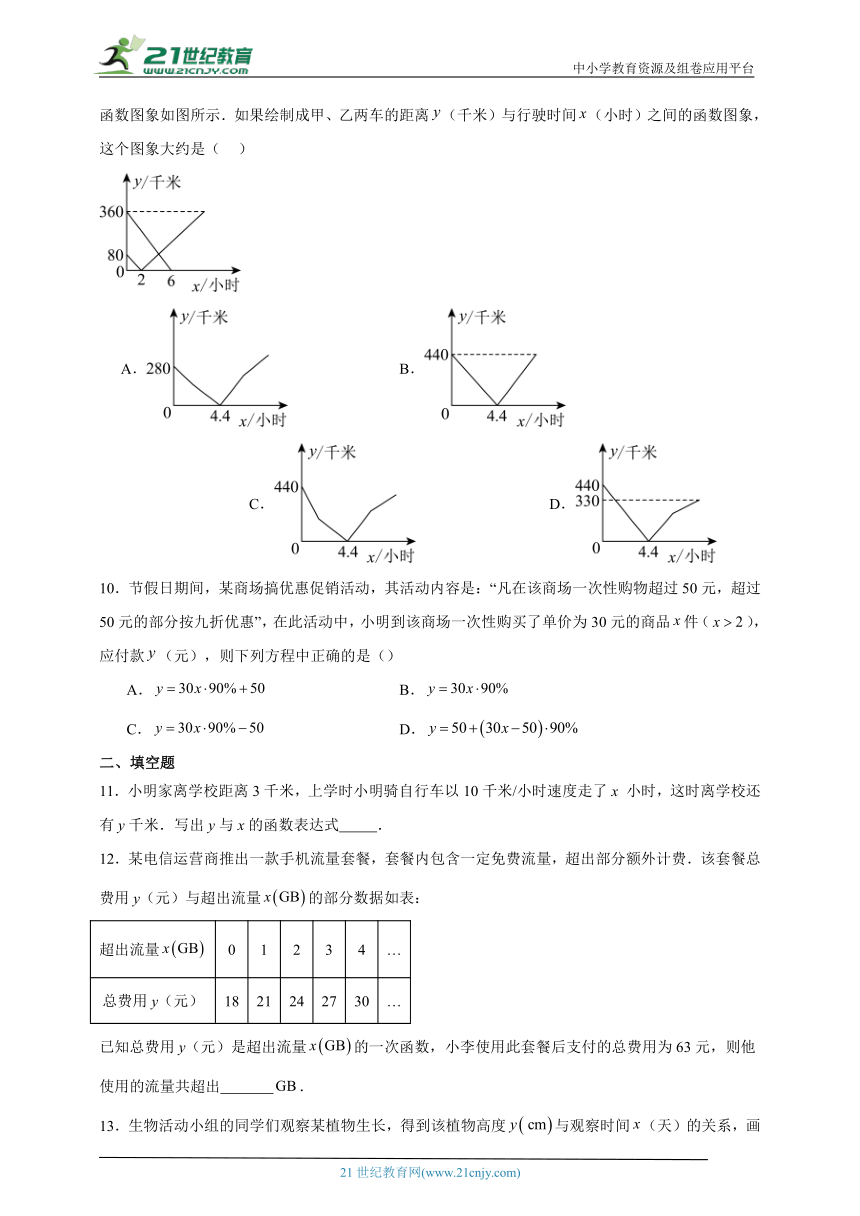
7.一辆货车从甲地匀速驶往乙地用了,到达后用了卸货.随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的2倍.货车离甲地的距离关于时间的函数图象如图所示,则a等于( )
A. B. C. D.
8.某水库在春季开闸放水用于农田灌溉,若开闸后水库水位与时间近似满足一次函数,则的取值范围为( )
A. B. C. D.
9.在两地之间有汽车站(在直线上),甲车由地驶往站,乙车由地驶往地,两车同时出发,匀速行驶.甲、乙两车离C站的路程,(千米)与行驶时间(小时)之间的函数图象如图所示.如果绘制成甲、乙两车的距离(千米)与行驶时间(小时)之间的函数图象,这个图象大约是( )
A. B. C. D.
10.节假日期间,某商场搞优惠促销活动,其活动内容是:“凡在该商场一次性购物超过50元,超过50元的部分按九折优惠”,在此活动中,小明到该商场一次性购买了单价为30元的商品件(),应付款(元),则下列方程中正确的是()
A. B.
C. D.
二、填空题
11.小明家离学校距离3千米,上学时小明骑自行车以10千米/小时速度走了x 小时,这时离学校还有y千米.写出y与x的函数表达式 .
12.某电信运营商推出一款手机流量套餐,套餐内包含一定免费流量,超出部分额外计费.该套餐总费用y(元)与超出流量的部分数据如表:
超出流量 0 1 2 3 4 …
总费用y(元) 18 21 24 27 30 …
已知总费用y(元)是超出流量的一次函数,小李使用此套餐后支付的总费用为63元,则他使用的流量共超出 .
13.生物活动小组的同学们观察某植物生长,得到该植物高度与观察时间(天)的关系,画出如图所示的函数图象(轴).则该植物最高长到 .
14.某电器进价为250元/台,售价为400元/台,若售出x台,售出x台的总利润为y元,则y与x之间的关系式为 .
15.一辆汽车加满油后,油箱中有汽油55升,汽车行驶时正常的耗油量为每千米0.1升,则加满油后,油箱中剩余的汽油量y(升)关于已行驶的里程的函数解析式为 .
三、解答题
16.金百超市经销某品牌童装,单价为每件50元时,每天销量为60件,当单价每件从50元降了20元时,一天销量为100件.设降x元时,一天的销量为y件.已知y是x的一次函数.
(1)求y与x之间的关系式;
(2)若某天销售童装80件,则该天童装的单价是多少
17.A、B两家超市平时以同样的价格出售相同的商品,暑假期间两家超市进行促销活动,促销方式如下:
A超市:所有商品按照原价打9折;
B超市:一次购物不超过200元的按原价,超过200元后超过部分的价格打8折.
(1)设商品原价为x元(),购物金额为y元,分别就两家超市的促销方式写出y关于x的函数表达式;
(2)促销期间,若小刚一次购物的商品原价为300元,他去哪家超市购物更省钱?说明理由.
18.随着交通安全意识的增强,某城镇居民开始积极购买头盔以保证骑行安全.某小商店购进种头盔个和种头盔个共需元,种头盔个和种头盔个共需元.
(1)求,两种头盔的单价各是多少元;
(2)若该商店计划用不超过元购进,两种头盔共个,销售个种头盔可获利元,销售1个种头盔可获利元,假如这些头盔能全部售出,请你帮商店设计利润最大的进货方案,并求出最大利润,说明理由.
19.某中学八年级甲乙两班商定举行一次远足研学活动,A、B两地相距10km,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地,乙班比甲班晚出发一小时,设甲班步行时间为x小时,甲、乙两班距离A地的距离分别为、千米,、与x的函数关系图象如图所示,根据图象解答下列问题:
(1)N点的横坐标是______;
(2)求出、与x的函数关系式;
(3)乙班出发多长时间,甲、乙两班相遇?
(4)甲班离出发地A地多远时,两班相距4千米?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B A B A C A D D
1.A
【分析】本题考查一次函数关系式,设截掉的最大的正方形的边长为,则余下部分的边长分别为、,根据剩余部分的周长建立等式即可得到答案.
【详解】解:设截掉的最大的正方形的边长为,则余下部分的边长分别为、,
根据题意,得
经整理,得.
故选:A.
2.B
【分析】根据记录表由待定系数法就可以求出y与x的函数表达式.
【详解】解:根据记录表知,每3 min钟,观光船与码头的距离缩短75m,
∴y与x的函数表达式为一次函数关系,
设y与x的函数表达式为y=kx+b,由记录表得:
,
解得:.
∴y与x的函数表达式为y=-25x+675.
当y=150时,150=-25x+675,
解得x=21,
∴从开始计时到观光船与码头的距离为150m时,所用时间为21min,
故选:B.
【点睛】本题考查了一次函数的应用,在解答时利用待定系数法求出一次函数解析式是关键.
3.B
【详解】试题分析:依题意设旅行社全票价为x元,三人旅行实际收费为y元.可知东方旅行社三人旅行实际收费为:y=2x+70%x=2.7x(元)而光明旅行社三人旅行实际收费为:=2.7x.可知两家旅行社实际收费相同.
考点:一次函数
点评:本题难度较低,分情况求一次函数y值最简便.学生易错在于没有分情况讨论.
4.A
【分析】设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,可得客车总数为6,,根据题意列出一次函数和一元一次不等式,找到x的取值范围,再结合一次函数的增减性即可求解.
【详解】解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
【点睛】本题考查一次函数和一元一次不等式的实际应用,利用题中的不等关系找到x的取值范围是解题的关键.
5.B
【分析】本题考查一元一次不等式的应用,涉及一次函数的应用,解题的关键是读懂题意,列出不等式求出的范围.
设该商场在这一时期内销售获得的利润是元,销售型饮水机台,则销售型饮水机台,根据在同一时期内,型饮水机的销售量不小于型饮水机销售量的3倍可得:,而,由一次函数性质可得答案.
【详解】解:设该商场在这一时期内销售获得的利润是元,销售型饮水机台,则销售型饮水机台,
根据题意得:.
解得:,
,
∴随的增大而减小,
∴当时,取最大值,最大值为(元),
答:该商场在这一时期内销售这两种饮水机能获得的最大利润是元.
故选:B.
6.A
【分析】利用图象交点得出公司盈利以及公司亏损情况.
【详解】解:A、当销售量为4台时,该公司赢利0万元,错误;
B、当销售量多于4台时,该公司才开始赢利,正确;
C、当销售量为2台时,该公司亏本1万元,正确;
D、当销售量为6台时,该公司赢利1万元,正确;
故选A.
【点睛】此题主要考查了一次函数的应用,熟练利用数形结合得出是解题关键.
7.C
【分析】本题考查了一次函数的图像的应用、方程组的应用,根据一次函数图像以及路程、速度和时间的关系列出方程组是解答本题的关键.
先根据路程、速度和时间的关系题意可得甲地到乙地的速度和从乙地到甲地的时间,再由货车返回的速度是它从甲地驶往乙地的速度的2倍,列出方程组求得从乙地到甲地的时间t,进而求得a的值.
【详解】解:设甲乙两地的路程为s,从甲地到乙地的速度为v,从乙地到甲地的时间为t,
则
解得,
∴(小时),
故选:C.
8.A
【分析】本题考查的是一次函数的实际应用,根据实际意义可得随的增大而减少,从而可得答案.
【详解】解:∵开闸后水库水位与时间近似满足一次函数,
∴随的增大而减少,
∴,
故选:A
9.D
【分析】本题考查了一次函数的应用,根据函数图象逐项判断即可求解,从函数图象获取必要的信息是解题的关键.
【详解】解:如图所示:
由函数图象可知,当时,,,
两地之间的距离是千米,两地之间的距离是千米,
千米,
两地相距千米,故选项不符合题意;
两车的速度和不变,
相遇前随的增大而减小,
故选项不符合题意;
甲车到达站后,甲、乙两车的距离随的增加而增加且增加的速度比开始小,
选项不符合题意,选项符合题意,
故选:.
10.D
【分析】此题主要考查了根据实际问题列一次函数解析式,根据已知得出货款与商品件数的等式是解题关键.根据已知表示出买商品件的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:凡在该商场一次性购物超过50元,超过50元的部分按九折优惠,
小明到该商场一次性购买了单价为30元的商品件(),
则小明应付货款与商品件数的函数关系式是:,
故选:D.
11.y=3-10x/y=-10x+3
【分析】根据小明离学校的距离=小明家离学校距离-小明骑自行车行驶的距离,列出表达式即可.
【详解】解:∵小明家离学校距离3千米,上学时小明骑自行车以10千米/小时速度走了x 小时,
∴小明离学校的距离.
故答案为:.
【点睛】此题考查了一次函数的应用题,解题的关键是正确分析题目中的等量关系.
12.15
【分析】本题考查一次函数的应用,解题的关键是求出总费用y( 元)是超出流量的函数关系式.
求出总费用y( 元)是超出流量的函数关系式,在令y=63算出x的值即可.
【详解】解:由总费用y( 元)是超出流量的一次函数,设,
根据表格可得:,
解得,
∴,
令得,
解得,
∴他使用的流量共超出;
故答案为:15.
13.31
【分析】本题考查了一次函数的运用,理解图示,掌握待定系数法求一次函数解析式,一次函数图象的性质是解题的关键.
根据图示,设一次函数为,把点代入得到解析式,再把代入即可求解.
【详解】解:根据函数图象设一次函数为,把点代入得,
解得,,
∴一次函数解析式为,
当时,,
当时,,则该植物达到最高高度,
∴该植物最高长到,
故答案为:31 .
14.
【分析】本题考查了一次函数在销售问题中的应用,等量关系式:利润销售每台电器的利润销售量,此次即可求解;找出等量关系式是解题的关键.
【详解】解:由题意得
;
故答案:.
15.
【分析】本题考查函数关系式,根据题意得到变量之间的数量关系是解题的关键.
【详解】解:汽车耗油量为每千米升,
行驶km耗油升,
加满油后,油箱中剩余的汽油量.
故答案为:.
16.(1)y与x之间的关系式为y=2x+60
(2)该天童装的单价是每件40元
【分析】(1)根据题意先设出y与x的函数关系式y=kx+b,再根据题目中的数据,即可求出该函数的解析式;
(2)将y= 80代入(1) 中函数关系式,求出相应的x的值即可.
【详解】(1)因为y是x的一次函数.
所以,设y与x的函数关系式为y=kx+b,
由题意知,当x=0时, y=60 ;当x=20时, y= 100,
所以,
解之得:
所以y与x之间的关系式为y=2x+60 ;
(2)当y=80时,由80=2x+60,
解得x=10,
所以50- 10= 40(元),
所以该天童装的单价是每件40元.
【点睛】本题考查一次函数的应用, 解答本题的关键是明确题意,求出相应的函数关系式.
17.(1),
(2)甲超市更省钱,理由见解析
【分析】(1)根据题意列出函数关系式即可求解;
(2)将,代入(1)中解析式,继而比较即可求解.
【详解】(1)根据题意得,,
,
(2)甲超市更省钱,理由如下,
,
∴,
,
∵,
故甲超市更省钱.
【点睛】本题考查了一次函数的应用,根据题意列出函数关系式是解题的关键.
18.(1)种头盔的单价是元,种头盔的单价是元;
(2)购进类头盔个,类头盔个时,获得最大利润为元.理由见解析.
【分析】本题主要考查了二元一次方程组的应用、一元一次不等式的应用、一次函数的应用,解决本题的关键是根据一次函数的性质求最大利润.
设种头盔的单价是元,种头盔的单价是元,根据两种购买方式列出二元一次方程组,解方程组即可;
:设购进类头盔个,类头盔个,根据总费用不超过元,可得不等式,解不等式得到的取值范围;设总利润为元,根据每个头盔的利润可得一次函数,根据一次函数的性质可知的值越大,利润越,从而可知购进类头盔个,类头盔个时,获得最大利润为元.
【详解】(1)解:设种头盔的单价是元,种头盔的单价是元,
由题意得:,
解得,
答:种头盔的单价是元,种头盔的单价是元;
(2)解:设购进类头盔个,类头盔个,
则,
解得:,
设总利润为元,
则,
,
随的增大而增大,
当时,取得最大值元,
购进类头盔个,类头盔个时,获得最大利润为元.
19.(1)1
(2),
(3)乙班出发小时,甲,乙相遇
(4)甲班离出发地地米或米时,两班相距4千米
【分析】本题考查的是从函数图象中获取信息,一次函数的实际应用,理解题意是解本题的关键;
(1)由A、B两地相距10km,乙班比甲班晚出发一小时,从而可得答案;
(2)直接利用待定系数法求解、与x的函数关系式即可;
(3)联立两个函数解析式,再解方程组即可;
(4)利用两个函数解析式,建立方程求解即可.
【详解】(1)解:由题意可得:,
∴的横坐标为;
(2)设,把代入得:,
∴,
∴;
设,
把和代入得:,
解得,
,
(3)当时,,
解得,(小时),
答:乙班出发小时,甲,乙相遇;
(4)当时,
解得,
,
当时,
,
解得,
;
答:甲班离出发地地米或米时,两班相距4千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.3 课题学习 选择方案 同步试题
2024--2025学年初中数学人教版八年级下册
一、单选题
1.如图,大长方形的长为x,在左侧截掉一个面积最大的正方形. 若剩余部分的周长是y,则y与x的函数关系式是 ( )
A. B. C. D.
2.一条观光船沿直线向码头前进,下表记录了4个时间点观光船与码头的距离,其中t表示时间,y表示观光船与码头的距离.
0 3 6 9
675 600 525 450
如果观光船保持这样的行进状态继续前进,那么从开始计时到观光船与码头的距离为150m时,所用时间为( )
A.25min B.21min C.13min D.12min
3.暑假里父母带小明外出旅行,了解到东方旅行社规定:若父母各买一张全票,则孩子的 费用可按全票价七折优惠(即优惠30%);而光明旅行社规定:三人旅行可按团体票计价,即按全票价的90%收费,若已知旅行社的全票价相同,则实际收费( )
A.东方旅行社比光明旅行社低
B.东方旅行社与光明旅行社相同
C.东方旅行社比光明旅行社高
D.谁高谁低视全票价多少而定
4.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
5.某商场在促销活动中,计划销售型和型两种饮水机共20台.若每台型饮水机可盈利150元,每台型饮水机可盈利200元,型饮水机的销售量不小于型饮水机的3倍.则该商场在本次促销活动中销售这两种饮水机能获得的最大利润是( )
A.3400元 B.3250元 C.4600元 D.4750元
6.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
A.当销售量为4台时,该公司赢利4万元 B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元 D.当销售量为6台时,该公司赢利1万元
7.一辆货车从甲地匀速驶往乙地用了,到达后用了卸货.随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的2倍.货车离甲地的距离关于时间的函数图象如图所示,则a等于( )
A. B. C. D.
8.某水库在春季开闸放水用于农田灌溉,若开闸后水库水位与时间近似满足一次函数,则的取值范围为( )
A. B. C. D.
9.在两地之间有汽车站(在直线上),甲车由地驶往站,乙车由地驶往地,两车同时出发,匀速行驶.甲、乙两车离C站的路程,(千米)与行驶时间(小时)之间的函数图象如图所示.如果绘制成甲、乙两车的距离(千米)与行驶时间(小时)之间的函数图象,这个图象大约是( )
A. B. C. D.
10.节假日期间,某商场搞优惠促销活动,其活动内容是:“凡在该商场一次性购物超过50元,超过50元的部分按九折优惠”,在此活动中,小明到该商场一次性购买了单价为30元的商品件(),应付款(元),则下列方程中正确的是()
A. B.
C. D.
二、填空题
11.小明家离学校距离3千米,上学时小明骑自行车以10千米/小时速度走了x 小时,这时离学校还有y千米.写出y与x的函数表达式 .
12.某电信运营商推出一款手机流量套餐,套餐内包含一定免费流量,超出部分额外计费.该套餐总费用y(元)与超出流量的部分数据如表:
超出流量 0 1 2 3 4 …
总费用y(元) 18 21 24 27 30 …
已知总费用y(元)是超出流量的一次函数,小李使用此套餐后支付的总费用为63元,则他使用的流量共超出 .
13.生物活动小组的同学们观察某植物生长,得到该植物高度与观察时间(天)的关系,画出如图所示的函数图象(轴).则该植物最高长到 .
14.某电器进价为250元/台,售价为400元/台,若售出x台,售出x台的总利润为y元,则y与x之间的关系式为 .
15.一辆汽车加满油后,油箱中有汽油55升,汽车行驶时正常的耗油量为每千米0.1升,则加满油后,油箱中剩余的汽油量y(升)关于已行驶的里程的函数解析式为 .
三、解答题
16.金百超市经销某品牌童装,单价为每件50元时,每天销量为60件,当单价每件从50元降了20元时,一天销量为100件.设降x元时,一天的销量为y件.已知y是x的一次函数.
(1)求y与x之间的关系式;
(2)若某天销售童装80件,则该天童装的单价是多少
17.A、B两家超市平时以同样的价格出售相同的商品,暑假期间两家超市进行促销活动,促销方式如下:
A超市:所有商品按照原价打9折;
B超市:一次购物不超过200元的按原价,超过200元后超过部分的价格打8折.
(1)设商品原价为x元(),购物金额为y元,分别就两家超市的促销方式写出y关于x的函数表达式;
(2)促销期间,若小刚一次购物的商品原价为300元,他去哪家超市购物更省钱?说明理由.
18.随着交通安全意识的增强,某城镇居民开始积极购买头盔以保证骑行安全.某小商店购进种头盔个和种头盔个共需元,种头盔个和种头盔个共需元.
(1)求,两种头盔的单价各是多少元;
(2)若该商店计划用不超过元购进,两种头盔共个,销售个种头盔可获利元,销售1个种头盔可获利元,假如这些头盔能全部售出,请你帮商店设计利润最大的进货方案,并求出最大利润,说明理由.
19.某中学八年级甲乙两班商定举行一次远足研学活动,A、B两地相距10km,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地,乙班比甲班晚出发一小时,设甲班步行时间为x小时,甲、乙两班距离A地的距离分别为、千米,、与x的函数关系图象如图所示,根据图象解答下列问题:
(1)N点的横坐标是______;
(2)求出、与x的函数关系式;
(3)乙班出发多长时间,甲、乙两班相遇?
(4)甲班离出发地A地多远时,两班相距4千米?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B A B A C A D D
1.A
【分析】本题考查一次函数关系式,设截掉的最大的正方形的边长为,则余下部分的边长分别为、,根据剩余部分的周长建立等式即可得到答案.
【详解】解:设截掉的最大的正方形的边长为,则余下部分的边长分别为、,
根据题意,得
经整理,得.
故选:A.
2.B
【分析】根据记录表由待定系数法就可以求出y与x的函数表达式.
【详解】解:根据记录表知,每3 min钟,观光船与码头的距离缩短75m,
∴y与x的函数表达式为一次函数关系,
设y与x的函数表达式为y=kx+b,由记录表得:
,
解得:.
∴y与x的函数表达式为y=-25x+675.
当y=150时,150=-25x+675,
解得x=21,
∴从开始计时到观光船与码头的距离为150m时,所用时间为21min,
故选:B.
【点睛】本题考查了一次函数的应用,在解答时利用待定系数法求出一次函数解析式是关键.
3.B
【详解】试题分析:依题意设旅行社全票价为x元,三人旅行实际收费为y元.可知东方旅行社三人旅行实际收费为:y=2x+70%x=2.7x(元)而光明旅行社三人旅行实际收费为:=2.7x.可知两家旅行社实际收费相同.
考点:一次函数
点评:本题难度较低,分情况求一次函数y值最简便.学生易错在于没有分情况讨论.
4.A
【分析】设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,可得客车总数为6,,根据题意列出一次函数和一元一次不等式,找到x的取值范围,再结合一次函数的增减性即可求解.
【详解】解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
【点睛】本题考查一次函数和一元一次不等式的实际应用,利用题中的不等关系找到x的取值范围是解题的关键.
5.B
【分析】本题考查一元一次不等式的应用,涉及一次函数的应用,解题的关键是读懂题意,列出不等式求出的范围.
设该商场在这一时期内销售获得的利润是元,销售型饮水机台,则销售型饮水机台,根据在同一时期内,型饮水机的销售量不小于型饮水机销售量的3倍可得:,而,由一次函数性质可得答案.
【详解】解:设该商场在这一时期内销售获得的利润是元,销售型饮水机台,则销售型饮水机台,
根据题意得:.
解得:,
,
∴随的增大而减小,
∴当时,取最大值,最大值为(元),
答:该商场在这一时期内销售这两种饮水机能获得的最大利润是元.
故选:B.
6.A
【分析】利用图象交点得出公司盈利以及公司亏损情况.
【详解】解:A、当销售量为4台时,该公司赢利0万元,错误;
B、当销售量多于4台时,该公司才开始赢利,正确;
C、当销售量为2台时,该公司亏本1万元,正确;
D、当销售量为6台时,该公司赢利1万元,正确;
故选A.
【点睛】此题主要考查了一次函数的应用,熟练利用数形结合得出是解题关键.
7.C
【分析】本题考查了一次函数的图像的应用、方程组的应用,根据一次函数图像以及路程、速度和时间的关系列出方程组是解答本题的关键.
先根据路程、速度和时间的关系题意可得甲地到乙地的速度和从乙地到甲地的时间,再由货车返回的速度是它从甲地驶往乙地的速度的2倍,列出方程组求得从乙地到甲地的时间t,进而求得a的值.
【详解】解:设甲乙两地的路程为s,从甲地到乙地的速度为v,从乙地到甲地的时间为t,
则
解得,
∴(小时),
故选:C.
8.A
【分析】本题考查的是一次函数的实际应用,根据实际意义可得随的增大而减少,从而可得答案.
【详解】解:∵开闸后水库水位与时间近似满足一次函数,
∴随的增大而减少,
∴,
故选:A
9.D
【分析】本题考查了一次函数的应用,根据函数图象逐项判断即可求解,从函数图象获取必要的信息是解题的关键.
【详解】解:如图所示:
由函数图象可知,当时,,,
两地之间的距离是千米,两地之间的距离是千米,
千米,
两地相距千米,故选项不符合题意;
两车的速度和不变,
相遇前随的增大而减小,
故选项不符合题意;
甲车到达站后,甲、乙两车的距离随的增加而增加且增加的速度比开始小,
选项不符合题意,选项符合题意,
故选:.
10.D
【分析】此题主要考查了根据实际问题列一次函数解析式,根据已知得出货款与商品件数的等式是解题关键.根据已知表示出买商品件的总钱数以及优惠后价格,进而得出等式即可.
【详解】解:凡在该商场一次性购物超过50元,超过50元的部分按九折优惠,
小明到该商场一次性购买了单价为30元的商品件(),
则小明应付货款与商品件数的函数关系式是:,
故选:D.
11.y=3-10x/y=-10x+3
【分析】根据小明离学校的距离=小明家离学校距离-小明骑自行车行驶的距离,列出表达式即可.
【详解】解:∵小明家离学校距离3千米,上学时小明骑自行车以10千米/小时速度走了x 小时,
∴小明离学校的距离.
故答案为:.
【点睛】此题考查了一次函数的应用题,解题的关键是正确分析题目中的等量关系.
12.15
【分析】本题考查一次函数的应用,解题的关键是求出总费用y( 元)是超出流量的函数关系式.
求出总费用y( 元)是超出流量的函数关系式,在令y=63算出x的值即可.
【详解】解:由总费用y( 元)是超出流量的一次函数,设,
根据表格可得:,
解得,
∴,
令得,
解得,
∴他使用的流量共超出;
故答案为:15.
13.31
【分析】本题考查了一次函数的运用,理解图示,掌握待定系数法求一次函数解析式,一次函数图象的性质是解题的关键.
根据图示,设一次函数为,把点代入得到解析式,再把代入即可求解.
【详解】解:根据函数图象设一次函数为,把点代入得,
解得,,
∴一次函数解析式为,
当时,,
当时,,则该植物达到最高高度,
∴该植物最高长到,
故答案为:31 .
14.
【分析】本题考查了一次函数在销售问题中的应用,等量关系式:利润销售每台电器的利润销售量,此次即可求解;找出等量关系式是解题的关键.
【详解】解:由题意得
;
故答案:.
15.
【分析】本题考查函数关系式,根据题意得到变量之间的数量关系是解题的关键.
【详解】解:汽车耗油量为每千米升,
行驶km耗油升,
加满油后,油箱中剩余的汽油量.
故答案为:.
16.(1)y与x之间的关系式为y=2x+60
(2)该天童装的单价是每件40元
【分析】(1)根据题意先设出y与x的函数关系式y=kx+b,再根据题目中的数据,即可求出该函数的解析式;
(2)将y= 80代入(1) 中函数关系式,求出相应的x的值即可.
【详解】(1)因为y是x的一次函数.
所以,设y与x的函数关系式为y=kx+b,
由题意知,当x=0时, y=60 ;当x=20时, y= 100,
所以,
解之得:
所以y与x之间的关系式为y=2x+60 ;
(2)当y=80时,由80=2x+60,
解得x=10,
所以50- 10= 40(元),
所以该天童装的单价是每件40元.
【点睛】本题考查一次函数的应用, 解答本题的关键是明确题意,求出相应的函数关系式.
17.(1),
(2)甲超市更省钱,理由见解析
【分析】(1)根据题意列出函数关系式即可求解;
(2)将,代入(1)中解析式,继而比较即可求解.
【详解】(1)根据题意得,,
,
(2)甲超市更省钱,理由如下,
,
∴,
,
∵,
故甲超市更省钱.
【点睛】本题考查了一次函数的应用,根据题意列出函数关系式是解题的关键.
18.(1)种头盔的单价是元,种头盔的单价是元;
(2)购进类头盔个,类头盔个时,获得最大利润为元.理由见解析.
【分析】本题主要考查了二元一次方程组的应用、一元一次不等式的应用、一次函数的应用,解决本题的关键是根据一次函数的性质求最大利润.
设种头盔的单价是元,种头盔的单价是元,根据两种购买方式列出二元一次方程组,解方程组即可;
:设购进类头盔个,类头盔个,根据总费用不超过元,可得不等式,解不等式得到的取值范围;设总利润为元,根据每个头盔的利润可得一次函数,根据一次函数的性质可知的值越大,利润越,从而可知购进类头盔个,类头盔个时,获得最大利润为元.
【详解】(1)解:设种头盔的单价是元,种头盔的单价是元,
由题意得:,
解得,
答:种头盔的单价是元,种头盔的单价是元;
(2)解:设购进类头盔个,类头盔个,
则,
解得:,
设总利润为元,
则,
,
随的增大而增大,
当时,取得最大值元,
购进类头盔个,类头盔个时,获得最大利润为元.
19.(1)1
(2),
(3)乙班出发小时,甲,乙相遇
(4)甲班离出发地地米或米时,两班相距4千米
【分析】本题考查的是从函数图象中获取信息,一次函数的实际应用,理解题意是解本题的关键;
(1)由A、B两地相距10km,乙班比甲班晚出发一小时,从而可得答案;
(2)直接利用待定系数法求解、与x的函数关系式即可;
(3)联立两个函数解析式,再解方程组即可;
(4)利用两个函数解析式,建立方程求解即可.
【详解】(1)解:由题意可得:,
∴的横坐标为;
(2)设,把代入得:,
∴,
∴;
设,
把和代入得:,
解得,
,
(3)当时,,
解得,(小时),
答:乙班出发小时,甲,乙相遇;
(4)当时,
解得,
,
当时,
,
解得,
;
答:甲班离出发地地米或米时,两班相距4千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
