学科融合问题常考考点 预测练 2025年中考数学三轮复习备考
文档属性
| 名称 | 学科融合问题常考考点 预测练 2025年中考数学三轮复习备考 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
学科融合问题常考考点 预测练
2025年中考数学三轮复习备考
一、单选题
1.2025年春节,是中国“春节”申遗成功后的首个农历新年.连云港市各大旅游景区人流如潮,文旅市场呈现出“年味浓、人气旺、消费热”的繁荣景象.2025年春节期间,连云港全市接待游客约2390000人次.数据2390000用科学记数法表示为( )
A. B. C. D.
2.“成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“水涨船高”,④“瓜熟蒂落”描述的事件是不可能事件的是( )
A.① B.② C.③ D.④
3.等高线指的是地形图上海拔相等的相邻各点所连成的闭合曲线,在等高线上标注的数字为该等高线的海拔.若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为( )
A.米 B.米 C.米 D.米
4.【跨学科】已知蓄电池的电压为定值,在其工作时电流I(单位:A)与电阻R (单位:Ω)成反比; 当接入电路的电阻为8Ω时,其电流为3A,当电阻增大4Ω后,流经该电阻的电流( )
A.增大1A B.减小1A C.增大2A D.减小2A
5.2025年“体重管理年”正式启动,其中所涉及的体质指数“”是衡量人体胖瘦程度的标准,其计算公式为(表示体重,单位:公斤;表示身高,单位:米)成年人火女值标准见下表:
范围
胖瘦程度 瘦弱 偏瘦 正常 偏胖 肥胖
已知某位成年人身高为1.6米,以下说法正确的是( )
A.数值随着体重的值的增加而减少
B.数值与体重的值之间成正比例关系
C.数值与体重的值之间的函数图像为双曲线位于第一象限的一支
D.如果这位成年人的体重为64公斤,他的胖瘦程度属于正常
6.某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据如下表(频率结果精确到):
种子数
发芽数
发芽频率
依据上面的数据可以估计这种植物种子在该实验条件下发芽的概率是( )
A. B. C. D.
7.某校化学实验小组利用白醋和小苏打自制火箭发射小实验,如图,一枚自制小火箭从发射点A处发射,身高1.8米的小明在离发射点A距离的B处,当小火箭到达C点时,小明测得此刻的仰角为,则这枚小火此时的高度是( )
A. B.
C. D.
8.一个人的血压与其年龄及性别有关,对女性来说,正常的收缩压(毫米汞柱)与年龄(岁)大致满足关系:.如果一个女性的收缩压为110毫米汞柱,那么她的年龄是( )岁
A.15 B.20 C.30 D.35
9.小明在物理课上学习了物态变化相关知识后,自己在家中进行了“探究冰熔化时温度变化规律”的实验,并绘制了如图所示的此物质变化时的温度 时间图像.已知,冰在熔化过程中,温度不变.根据图像,下列说法错误的是( )
A.冰的整个熔化过程持续了
B.第时,冰仍在熔化,处于固液共存的状态
C.由图像可知,冰在第时全部熔化成水
D.由图像可知,冰的熔点是
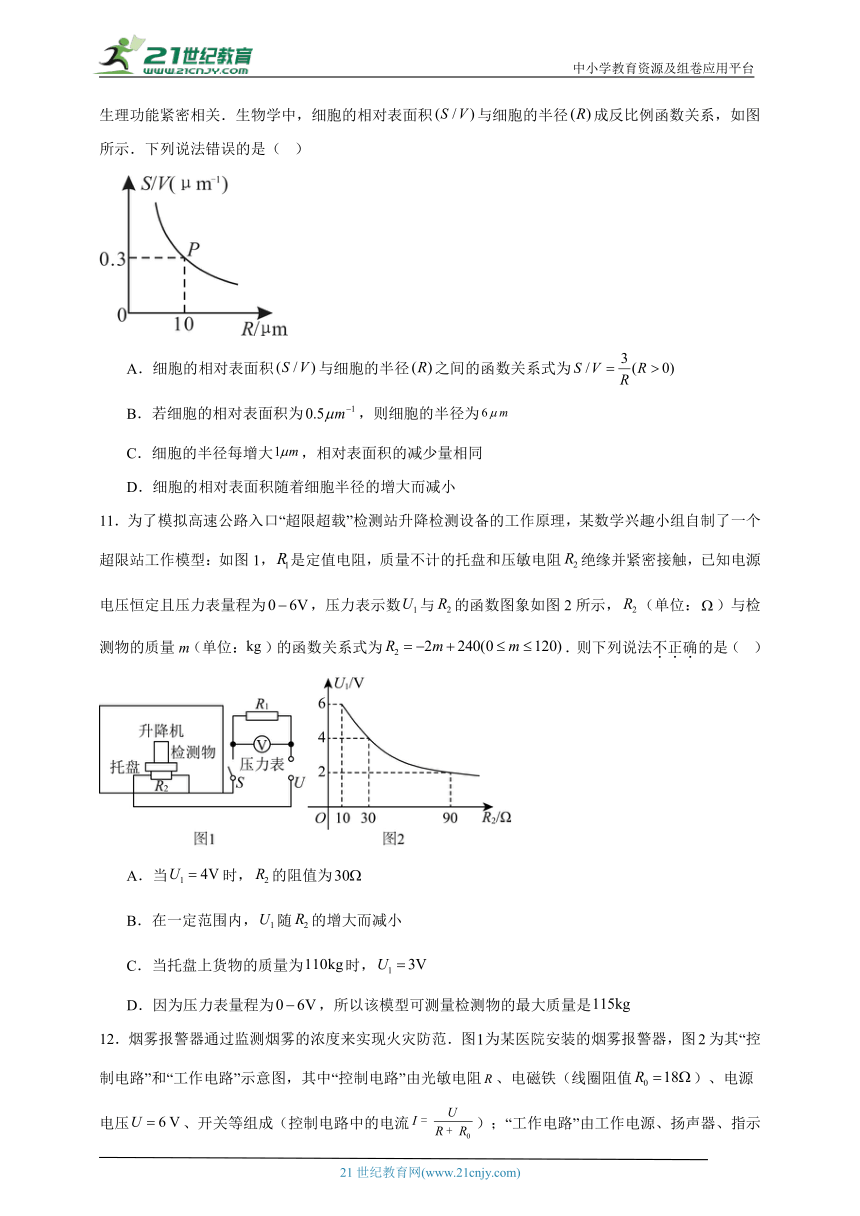
10.细胞的相对表面积是一个关键概念,指细胞的表面积与其体积的比率.它与细胞的大小和生理功能紧密相关.生物学中,细胞的相对表面积与细胞的半径成反比例函数关系,如图所示.下列说法错误的是( )
A.细胞的相对表面积与细胞的半径之间的函数关系式为
B.若细胞的相对表面积为,则细胞的半径为
C.细胞的半径每增大,相对表面积的减少量相同
D.细胞的相对表面积随着细胞半径的增大而减小
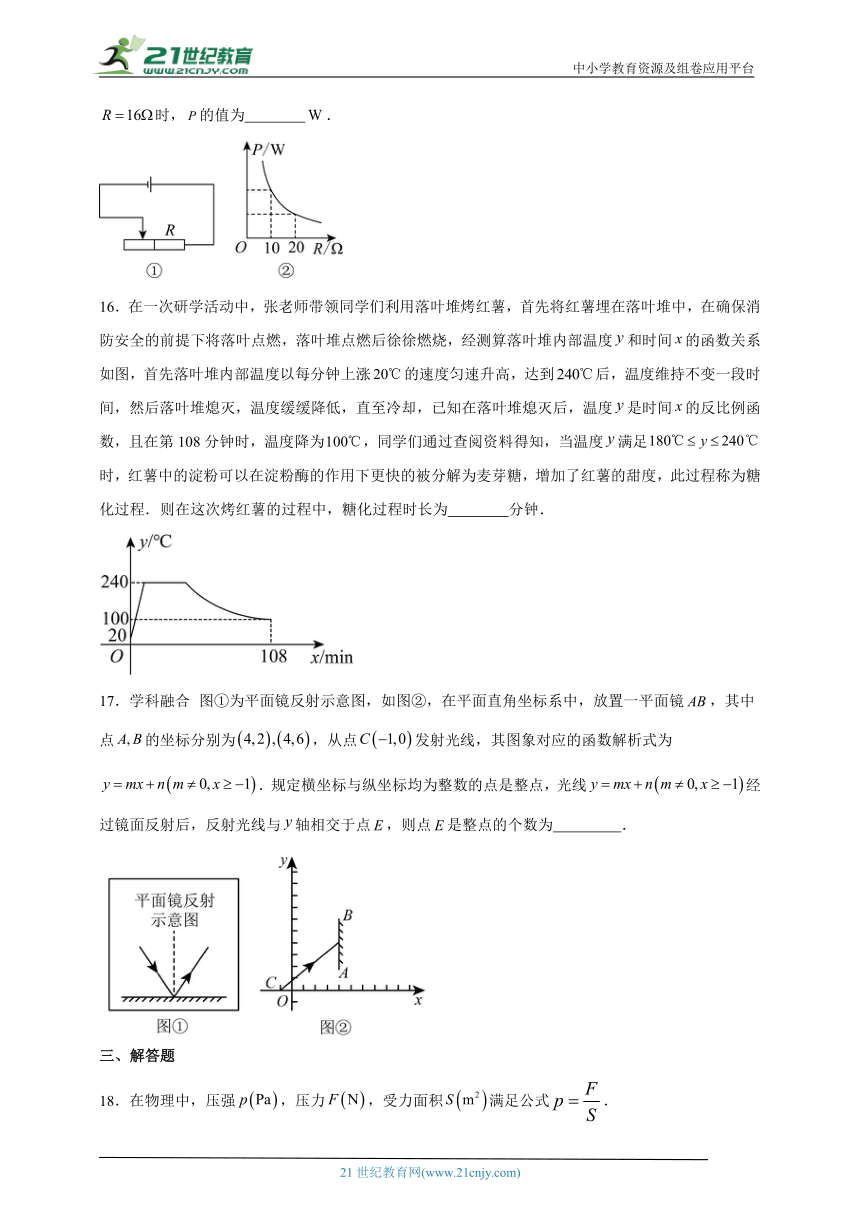
11.为了模拟高速公路入口“超限超载”检测站升降检测设备的工作原理,某数学兴趣小组自制了一个超限站工作模型:如图1,是定值电阻,质量不计的托盘和压敏电阻绝缘并紧密接触,已知电源电压恒定且压力表量程为,压力表示数与的函数图象如图2所示,(单位:)与检测物的质量m(单位:)的函数关系式为.则下列说法不正确的是( )
A.当时,的阻值为
B.在一定范围内,随的增大而减小
C.当托盘上货物的质量为时,
D.因为压力表量程为,所以该模型可测量检测物的最大质量是
12.烟雾报警器通过监测烟雾的浓度来实现火灾防范.图为某医院安装的烟雾报警器,图为其“控制电路”和“工作电路”示意图,其中“控制电路”由光敏电阻、电磁铁(线圈阻值)、电源电压、开关等组成(控制电路中的电流);“工作电路”由工作电源、扬声器、指示灯、导线等组成.其工作原理:正常情况下,动触片与触点接触,指示灯正常工作.当有烟雾时,光敏电阻接收到的光照强度减弱,当减弱到一定程度时,动触片与触点接触,扬声器发出报警声,已知触发报警器报警的电流不变.图为光敏电阻(单位:)与光照强度(单位:)之间的关系图象,则下列说法不正确的是( )
A.光敏电阻的阻值随光照强度的增大而减小
B.当光敏电阻的阻值为时,光照强度为
C.若使得烟雾报警器可以在更低浓度的烟雾下报警,可以使控制电路电压适当增大
D.当光照强度为时,控制电路中的电流为
二、填空题
13.如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算的距离,他在点处测得处的俯角为,则 m.
14.在温度不变的条件下,通过一次又一次地对汽缸(图1)顶部的活塞加压,加压后气体对汽缸壁所产生的压强是汽缸内气体的体积的反比例函数,p关于V的函数图象如图2所示.若压强由加压到,则气体体积压缩了 .
15.图①是某电路图,滑动变阻器为,电源电压为,电功率为,关于的函数图象如图②所示.嘉嘉通过两次调节电阻,发现当从增加到时,电功率减少了,则当时,的值为 .
16.在一次研学活动中,张老师带领同学们利用落叶堆烤红薯,首先将红薯埋在落叶堆中,在确保消防安全的前提下将落叶点燃,落叶堆点燃后徐徐燃烧,经测算落叶堆内部温度和时间的函数关系如图,首先落叶堆内部温度以每分钟上涨的速度匀速升高,达到后,温度维持不变一段时间,然后落叶堆熄灭,温度缓缓降低,直至冷却,已知在落叶堆熄灭后,温度是时间的反比例函数,且在第108分钟时,温度降为,同学们通过查阅资料得知,当温度满足时,红薯中的淀粉可以在淀粉酶的作用下更快的被分解为麦芽糖,增加了红薯的甜度,此过程称为糖化过程.则在这次烤红薯的过程中,糖化过程时长为 分钟.
17.学科融合 图①为平面镜反射示意图,如图②,在平面直角坐标系中,放置一平面镜,其中点的坐标分别为,从点发射光线,其图象对应的函数解析式为.规定横坐标与纵坐标均为整数的点是整点,光线经过镜面反射后,反射光线与轴相交于点,则点是整点的个数为 .
三、解答题
18.在物理中,压强,压力,受力面积满足公式.
(1)下面的函数图象,正确的有____________;填写序号)
(2)已知一块比较薄的冰面最多承受的压强,小明的重量为.
①若小明的一双鞋底与冰面的接触面积共,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
19.碧玉妆成一树高,万条垂下绿丝绦.阳春三月,垂柳吐绿,生机盎然,依依垂柳的新芽,形成一道美丽的风景.如图1是某公园的一棵垂柳(局部),这棵垂柳中某一枝的形状呈如图2所示的抛物线形,它距离地面的高度与到树干的水平距离之间满足关系式(为常数),已知这枝柳条的始端A到地面的距离,末端B恰好距离水平地面处,且末端B到树干(y轴)的水平距离为.(注:树干近似看作直线,且与地面垂直,无风,柳条不动)
(1)求该抛物线的函数表达式;
(2)王刚的身高为,他从点O出发沿x轴正方向走,请计算王刚走了多少米时,头顶恰好碰到这枝柳条?
20.二级火箭的始祖“火龙出水”的第一级火箭点燃后,会推动整个装置飞行,形成一个抛物线轨迹.当第一级火箭燃料耗尽时,火箭会下降到某个高度(这个高度低于最高点),此时自动引发火箭第二级,火箭第二级沿直线运行.可用函数图像模拟火箭的运行过程:如图,以发射点为原点,地平线为x轴,建立平面直角坐标系,分别得到抛物线和直线.其中,当火箭运行的水平距离为时,自动引发火箭的第二级.若火箭第二级的引发点的高度为.
(1)求出a,k的值;
(2)火箭在运行过程中,有两个位置的高度比火箭运行的最高点低,求这两个位置之间的距离.
21.【综合实践】
如图1所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境,受桔槔的启发,小杰组装了如图2所示的装置.其中,杠杆可绕支点O在竖直平面内转动,支点O距左端,距右端,在杠杆左端悬挂重力为的物体A.(杠杆原理:阻力×阻力臂=动力×动力臂,如图2,即)
… b …
… 8 a 2 …
(1)若在杠杆右端挂重物B,杠杆在水平位置平衡时,重物B所受拉力为 N;
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为,的长度为.则:
①y关于x的函数关系式是 .
②完成表格: ; .
③借助表格,在图3的直角坐标系中画出该函数的图象.
(3)在(2)的条件下,若点A的坐标为,点B的坐标为,在(2)中所求函数的图象上存在点C,使得,请求出点C的坐标.
22.[综合探究]运用二次函数来研究植物幼苗叶片的生长状况.在大自然里,有很多数学的奥秘.图1是一片美丽的心形叶片,图2是一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.
【探究一】确定心形叶片的形状
(1)如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数图象的一部分,已知图像过原点,求抛物线的解析式及顶点的坐标;
【探究二】研究心形叶片的宽度:
(2)如图3,在(1)的条件下,心形叶片的对称轴,即直线与坐标轴交于,两点,抛物线与轴交于另一点,点,是叶片上的一对对称点,交直线于点.求叶片此处的宽度;
【探究三】探究幼苗叶片的长度
(3)小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数图象的一部分;如图4,幼苗叶片下方轮廓线正好对应探究一中的二次函数.已知直线(点为叶尖)与水平线的夹角为,求幼苗叶片的长度.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B C A A B C
题号 11 12
答案 C C
1.B
【分析】根据科学记数法的方法进行解题即可.本题主要考查了用科学记数法表示较大的数,一般形式为,其中,为正整数,确定a与n的值是解题的关键.
【详解】解:依题意,数据2390000用科学记数法表示为,
故选:B
2.A
【分析】本题考查的是随机事件,必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.
【详解】解:①“水中捞月”,是不可能事件;
②“守株待兔”,是随机事件;
③“水涨船高”,是必然事件;
④“瓜熟蒂落”,是必然事件;
故选:A.
3.A
【分析】本题考查正数和负数的实际应用,若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为米,即可求解.
【详解】解:若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为米,
故选:A.
4.B
【分析】本题主要考查了反比例函数关系式,
根据工作电流与电阻成反比可得,再求出关系式,然后令求出电流,进而得出答案.
【详解】解:根据题意设反比例函数关系式为,
当时,
.
∴反比例函数关系式为,
当时,,
可知,
所以流经电阻的电流减少1A.
故选:B.
5.B
【分析】本题考查了反比例函数的性质、反比例函数图象上点的坐标特征、一次函数的应用,根据题意及反比例函数图象上点的坐标特征,逐项分析判断即可.
【详解】解:A、某位成年人身高为1.6米,数值随着体重m的值的增加而增加,原说法错误,不符合题意;
B、某位成年人身高为1.6米,数值与体重m的值之间成正比例关系,原说法正确,符合题意;
C、某位成年人身高为1.6米,数值与体重m的值之间的函数图象为第一象限内的直线,原说法错误,不符合题意;
D、某位成年人身高为1.6米,这位成年人的体重为64公斤,则数值是25,属于偏胖,原说法错误,不符合题意;
故选:B.
6.C
【分析】此题主要考查了利用频率估计概率,掌握以上知识点是解答本题的关键.
概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率.
【详解】解:因为概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率,
这种植物种子在该实验条件下发芽的概率是,
故选:C.
7.A
【分析】此题考查了解直角三角形的应用,过点D作于点E,则,证明四边形是矩形,则,,由得到,即可得到答案.
【详解】解:过点D作于点E,则,
∵,
∴四边形是矩形,
∴,
在中,,
∴
∴
故选:A
8.A
【分析】本题考查了二次函数的基本应用,直接把代入函数,解出即可得解.
【详解】解:当时,.
解得,(舍),
故这个女性的年龄为15岁,
故选:A.
9.B
【分析】本题考查函数图像,从函数图像中获取信息,逐一进行判断即可.
【详解】解:A、冰的整个熔化过程持续了;原说法正确,不符合题意;
B、第时,冰已经全部熔化,处于液体状态;原说法错误,符合题意;
C、由图像可知,冰在第时全部熔化成水;原说法正确,不符合题意;
D、由图像可知,冰的熔点是;原说法正确,不符合题意;
故选B.
10.C
【分析】本题考查了反比例函数的实际应用,根据反比例函数的性质逐一排除即可,熟练掌握反比例函数的性质是关键.
【详解】解:、设细胞的相对表面积与细胞的半径之间的函数关系式为,
当,,
∴,
∴函数关系式为,原选项正确,不符合题意;
、若细胞的相对表面积为,则细胞的半径为,原选项正确,不符合题意;
、细胞的半径每增大,相对表面积的减少量不相同,原选项错误,符合题意;
、细胞的相对表面积随着细胞半径的增大而减小,原选项正确,不符合题意;
故选:.
11.C
【分析】本题考查了反比例函数,解题的关键是理解题意,能够根据函数图象获取信息.
根据所给函数图像即可判断选项A、B,根据函数图象得与的函数关系,根据与m之间的关系得,进行计算即可判断选项C,当时,的阻值为,此时有最大值,进行计算即可判断选项D.
【详解】解:根据图 2 得,当时,的阻值为,故选项A说法正确;
在一定范围内,随的增大而减小,故选项B说法正确;
设与的函数关系为,
将代入得,
故与的函数关系为,
当托盘上货物的质量为时,令,,
则,故选项C说法错误,符合题意;
当时,的阻值为,最小,此时有最大值,即,
解得:,
即电压表量程为,为保护电压表,该电子体重秤可称的最大质量是,故选项D正确;
故选:C.
12.C
【分析】本题主要考查了反比例函数的图象与性质,熟练掌握反比例函数的图象与性质是解答本题的关键.
根据反比函数的图象与性质逐项判断即可.
【详解】A、由题图可知光敏电阻的直值随光照强度的增大雨减小,故A选项正确;
B、由题图可知图象上点的横、纵坐标之积为定值,可得,将代入反比例函数,得;
C、要使报警器在浓度更低的烟雾下报警,此时光照强度增强,由题图,可知光的电阻的阻值减小,从而控制电路的总电阻减小.因为触发投资器报警的电流不交,由,可知应减小控制电路电压,故C选项错误;
D、当光照强度为时,可知光敏电阻控制电路中的电流,故D选项正确;
故选 C.
13.100
【分析】本题是跨学科综合题.根据由等高线可知、两地的高度差为50米,然后点处测得处的俯角为求值即可.
【详解】解:由等高线可得、两地的实际高度差为,
依题意作图得:,,,
∴
故答案为:100.
14.90
【分析】本题考查待定系数法求反比例函数解析式,已知函数值求自变量值等.根据题意先设解析式为,代入得出反比例解析式,再将压强和分别代入求出自变量值再做减法即可.
【详解】解:设反比例函数解析式为:,
将代入中得:,
∴反比例解析式为:,
∴当压强为时,,
当压强为时,,
∴压强由加压到,则气体体积压缩了:,
故答案为:90.
15.25
【分析】本题考查了反比例函数的应用,根据反比例函数的图象的性质结合题意可得方程,据此可得P的值,进而得出的值,再把代入函数关系式解答即可.
【详解】解:根据题意得:,
解得,
∴,
∴,
当时,,
即当时,P的值为,
故答案为:25.
16.52
【分析】本题考查反比例函数的实际应用,求出反比例函数的解析式,求出温度上升至和下降到时的时间,进行求解即可.
【详解】解:设反比例函数的解析式为:,
由图象,把点代入,得:,
∴,
当时,,
∵刚燃烧时,落叶堆内部温度以每分钟上涨的速度匀速升高,
∴当温度上升到时,所需时间为:,
∴糖化过程时长为;
故答案为:.
17.7
【分析】本题考查待定系数法求函数解析式,一次函数图象及性质,作出点C关于对称点,可知的坐标,作直线,,分别求出这两条直线与y轴交点,则点E坐标即在范围内,即可得到整数点的个数,熟练掌握一次函数的性质是解答本题的关键.
【详解】解:如图,作点关于的对称点,则,
作直线分别交轴于,设直线的函数解析式为,
把和代入中,得,
解得,
点的坐标为.
设直线的函数解析式为,
把和代入中,得,
解得,
点的坐标为,
点纵坐标的取值范围为,
点是整点的有,共7个,
故答案为:.
18.(1)
(2)这块薄木板的面积至少.
【分析】本题考查了函数的图象,反比例函数的应用,掌握函数图象的特点是解题的关键.
()根据函数解析式即可判断求解;
()把,代入计算即可求解;
把,代入计算即可求解;
【详解】(1)解:当为定值时,是的反比例函数,故正确;
当为定值时,,是的正比例函数,故错误;
当为定值时,是的正比例函数,故正确;
∴正确的有,
故答案为:;
(2)解:把,代入
得,,
∵,
∴小明不能安全地站在这块冰面上;
把,代入得,,
解得,
∴这块薄木板的面积至少.
19.(1)
(2)王刚走了时,头顶恰好碰到这枝柳条
【分析】本题主要考查了二次函数的应用,解题时要能熟练掌握并灵活运用二次函数的性质是关键.
(1)依据题意,得该抛物线经过点和点,进而建立方程组计算可以得解;
(2)依据题意,在中,令,从而可得,求出x后即可判断得解.
【详解】(1)解:由题意知,该抛物线经过点和点,
,
解得,
该抛物线的函数表达式为.
(2)在中,令,
.
(不合题意,舍去),.
王刚走了时,头顶恰好碰到这枝柳条.
20.(1),
(2)
【分析】本题考查了二次函数和一次函数的综合应用,涉及待定系数法求解析式,二次函数的图象和性质,一次函数的图象与性质等知识点,熟练掌握二次函数和一次函数的图象与性质是解题的关键.
(1)将分别代入抛物线和直线,即可求解;
(2)先求出比火箭运行的最高点低的高度,然后代入解析式,即可求解;
【详解】(1)解:∵火箭第二级的引发点的高度为,
∴抛物线和直线均经过点,
∴,,
解得:,;
(2)解:由①知:,,
∴,
∴最大值,
当时,,
解得:,,
又∵火箭运行的水平距离为时,自动引发火箭的第二级.而火箭第二级的引发点的高度为,
∴不合题意舍去;
∴当火箭第二级高度时,在第二级则,
解得:,
∴,
∴这两个位置之间的距离为.
21.(1)
(2)①;②4;;③见解析
(3)点C的坐标为或
【分析】(1)根据公式进行计算即可;
(2)①根据公式即可得到;②根据①求出a、b的值即可;③先描点,再连线,画出函数图像即可;
(3)设,连接,,,根据三角形的面积求出a的值.
【详解】(1)解:∵,
∴,
∴重物B所受拉力为,
故答案为:;
(2)解:①∵,
∴,即,
故答案为:;
②由①得,,
填表如下:
… …
… 8 4 2 …
故答案为:4,;
③函数图象如下所示:
;
(3)解:点A的坐标为,B的坐标为,C为反比例函数上一点,
设,连接,,,
∴
,
∵,
∴,
整理得:,
解得,,
经检验,或是原方程的根,
∴时;时,,
∴点C的坐标为或.
【点睛】本题是反比例函数的综合题,主要考查了待定系数法求反比例函数的解析式,三角形的面积,反比例函数的性质和图像,正确理解题意是解题的关键.
22.(1),顶点的坐标为;(2);(3)
【分析】(1)把原点代入解析式,求得值,将抛物线化成顶点式即可确定顶点坐标;
(2)先求出点的坐标为,再求出的解析式为:.然后求出点的坐标为,最后求出结果即可;
(3)作抛物线的对称轴于点,则,设点的横坐标为,得出,根据点在抛物线上,列出方程,得出点的坐标为,最后求出即可.
【详解】解:(1)抛物线经过原点,
.
解得:.
抛物线的解析式为:.
顶点的坐标为;
(2)取,,
解得:,,
点的坐标为,
心形叶片的对称轴是直线,点,是叶片上的一对对称点,
设的解析式为:.
经过点,
.
解得:.
的解析式为:.
,
解得:
点的坐标为.
.
.
(3)作抛物线的对称轴于点,则,
直线与水平线的夹角为,
.
设点的横坐标为,
抛物线的对称轴为直线,
.
顶点的坐标为,
点的纵坐标为.
点在抛物线上,
.
解得:.
点的坐标为.
.
【点睛】本题考查了待定系数法求解析式,等腰直角三角形的判定和性质,抛物线与坐标轴的交点,对称思想,两点间的距离公式,熟练掌握待定系数法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
学科融合问题常考考点 预测练
2025年中考数学三轮复习备考
一、单选题
1.2025年春节,是中国“春节”申遗成功后的首个农历新年.连云港市各大旅游景区人流如潮,文旅市场呈现出“年味浓、人气旺、消费热”的繁荣景象.2025年春节期间,连云港全市接待游客约2390000人次.数据2390000用科学记数法表示为( )
A. B. C. D.
2.“成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“水涨船高”,④“瓜熟蒂落”描述的事件是不可能事件的是( )
A.① B.② C.③ D.④
3.等高线指的是地形图上海拔相等的相邻各点所连成的闭合曲线,在等高线上标注的数字为该等高线的海拔.若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为( )
A.米 B.米 C.米 D.米
4.【跨学科】已知蓄电池的电压为定值,在其工作时电流I(单位:A)与电阻R (单位:Ω)成反比; 当接入电路的电阻为8Ω时,其电流为3A,当电阻增大4Ω后,流经该电阻的电流( )
A.增大1A B.减小1A C.增大2A D.减小2A
5.2025年“体重管理年”正式启动,其中所涉及的体质指数“”是衡量人体胖瘦程度的标准,其计算公式为(表示体重,单位:公斤;表示身高,单位:米)成年人火女值标准见下表:
范围
胖瘦程度 瘦弱 偏瘦 正常 偏胖 肥胖
已知某位成年人身高为1.6米,以下说法正确的是( )
A.数值随着体重的值的增加而减少
B.数值与体重的值之间成正比例关系
C.数值与体重的值之间的函数图像为双曲线位于第一象限的一支
D.如果这位成年人的体重为64公斤,他的胖瘦程度属于正常
6.某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据如下表(频率结果精确到):
种子数
发芽数
发芽频率
依据上面的数据可以估计这种植物种子在该实验条件下发芽的概率是( )
A. B. C. D.
7.某校化学实验小组利用白醋和小苏打自制火箭发射小实验,如图,一枚自制小火箭从发射点A处发射,身高1.8米的小明在离发射点A距离的B处,当小火箭到达C点时,小明测得此刻的仰角为,则这枚小火此时的高度是( )
A. B.
C. D.
8.一个人的血压与其年龄及性别有关,对女性来说,正常的收缩压(毫米汞柱)与年龄(岁)大致满足关系:.如果一个女性的收缩压为110毫米汞柱,那么她的年龄是( )岁
A.15 B.20 C.30 D.35
9.小明在物理课上学习了物态变化相关知识后,自己在家中进行了“探究冰熔化时温度变化规律”的实验,并绘制了如图所示的此物质变化时的温度 时间图像.已知,冰在熔化过程中,温度不变.根据图像,下列说法错误的是( )
A.冰的整个熔化过程持续了
B.第时,冰仍在熔化,处于固液共存的状态
C.由图像可知,冰在第时全部熔化成水
D.由图像可知,冰的熔点是
10.细胞的相对表面积是一个关键概念,指细胞的表面积与其体积的比率.它与细胞的大小和生理功能紧密相关.生物学中,细胞的相对表面积与细胞的半径成反比例函数关系,如图所示.下列说法错误的是( )
A.细胞的相对表面积与细胞的半径之间的函数关系式为
B.若细胞的相对表面积为,则细胞的半径为
C.细胞的半径每增大,相对表面积的减少量相同
D.细胞的相对表面积随着细胞半径的增大而减小
11.为了模拟高速公路入口“超限超载”检测站升降检测设备的工作原理,某数学兴趣小组自制了一个超限站工作模型:如图1,是定值电阻,质量不计的托盘和压敏电阻绝缘并紧密接触,已知电源电压恒定且压力表量程为,压力表示数与的函数图象如图2所示,(单位:)与检测物的质量m(单位:)的函数关系式为.则下列说法不正确的是( )
A.当时,的阻值为
B.在一定范围内,随的增大而减小
C.当托盘上货物的质量为时,
D.因为压力表量程为,所以该模型可测量检测物的最大质量是
12.烟雾报警器通过监测烟雾的浓度来实现火灾防范.图为某医院安装的烟雾报警器,图为其“控制电路”和“工作电路”示意图,其中“控制电路”由光敏电阻、电磁铁(线圈阻值)、电源电压、开关等组成(控制电路中的电流);“工作电路”由工作电源、扬声器、指示灯、导线等组成.其工作原理:正常情况下,动触片与触点接触,指示灯正常工作.当有烟雾时,光敏电阻接收到的光照强度减弱,当减弱到一定程度时,动触片与触点接触,扬声器发出报警声,已知触发报警器报警的电流不变.图为光敏电阻(单位:)与光照强度(单位:)之间的关系图象,则下列说法不正确的是( )
A.光敏电阻的阻值随光照强度的增大而减小
B.当光敏电阻的阻值为时,光照强度为
C.若使得烟雾报警器可以在更低浓度的烟雾下报警,可以使控制电路电压适当增大
D.当光照强度为时,控制电路中的电流为
二、填空题
13.如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算的距离,他在点处测得处的俯角为,则 m.
14.在温度不变的条件下,通过一次又一次地对汽缸(图1)顶部的活塞加压,加压后气体对汽缸壁所产生的压强是汽缸内气体的体积的反比例函数,p关于V的函数图象如图2所示.若压强由加压到,则气体体积压缩了 .
15.图①是某电路图,滑动变阻器为,电源电压为,电功率为,关于的函数图象如图②所示.嘉嘉通过两次调节电阻,发现当从增加到时,电功率减少了,则当时,的值为 .
16.在一次研学活动中,张老师带领同学们利用落叶堆烤红薯,首先将红薯埋在落叶堆中,在确保消防安全的前提下将落叶点燃,落叶堆点燃后徐徐燃烧,经测算落叶堆内部温度和时间的函数关系如图,首先落叶堆内部温度以每分钟上涨的速度匀速升高,达到后,温度维持不变一段时间,然后落叶堆熄灭,温度缓缓降低,直至冷却,已知在落叶堆熄灭后,温度是时间的反比例函数,且在第108分钟时,温度降为,同学们通过查阅资料得知,当温度满足时,红薯中的淀粉可以在淀粉酶的作用下更快的被分解为麦芽糖,增加了红薯的甜度,此过程称为糖化过程.则在这次烤红薯的过程中,糖化过程时长为 分钟.
17.学科融合 图①为平面镜反射示意图,如图②,在平面直角坐标系中,放置一平面镜,其中点的坐标分别为,从点发射光线,其图象对应的函数解析式为.规定横坐标与纵坐标均为整数的点是整点,光线经过镜面反射后,反射光线与轴相交于点,则点是整点的个数为 .
三、解答题
18.在物理中,压强,压力,受力面积满足公式.
(1)下面的函数图象,正确的有____________;填写序号)
(2)已知一块比较薄的冰面最多承受的压强,小明的重量为.
①若小明的一双鞋底与冰面的接触面积共,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
19.碧玉妆成一树高,万条垂下绿丝绦.阳春三月,垂柳吐绿,生机盎然,依依垂柳的新芽,形成一道美丽的风景.如图1是某公园的一棵垂柳(局部),这棵垂柳中某一枝的形状呈如图2所示的抛物线形,它距离地面的高度与到树干的水平距离之间满足关系式(为常数),已知这枝柳条的始端A到地面的距离,末端B恰好距离水平地面处,且末端B到树干(y轴)的水平距离为.(注:树干近似看作直线,且与地面垂直,无风,柳条不动)
(1)求该抛物线的函数表达式;
(2)王刚的身高为,他从点O出发沿x轴正方向走,请计算王刚走了多少米时,头顶恰好碰到这枝柳条?
20.二级火箭的始祖“火龙出水”的第一级火箭点燃后,会推动整个装置飞行,形成一个抛物线轨迹.当第一级火箭燃料耗尽时,火箭会下降到某个高度(这个高度低于最高点),此时自动引发火箭第二级,火箭第二级沿直线运行.可用函数图像模拟火箭的运行过程:如图,以发射点为原点,地平线为x轴,建立平面直角坐标系,分别得到抛物线和直线.其中,当火箭运行的水平距离为时,自动引发火箭的第二级.若火箭第二级的引发点的高度为.
(1)求出a,k的值;
(2)火箭在运行过程中,有两个位置的高度比火箭运行的最高点低,求这两个位置之间的距离.
21.【综合实践】
如图1所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境,受桔槔的启发,小杰组装了如图2所示的装置.其中,杠杆可绕支点O在竖直平面内转动,支点O距左端,距右端,在杠杆左端悬挂重力为的物体A.(杠杆原理:阻力×阻力臂=动力×动力臂,如图2,即)
… b …
… 8 a 2 …
(1)若在杠杆右端挂重物B,杠杆在水平位置平衡时,重物B所受拉力为 N;
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为,的长度为.则:
①y关于x的函数关系式是 .
②完成表格: ; .
③借助表格,在图3的直角坐标系中画出该函数的图象.
(3)在(2)的条件下,若点A的坐标为,点B的坐标为,在(2)中所求函数的图象上存在点C,使得,请求出点C的坐标.
22.[综合探究]运用二次函数来研究植物幼苗叶片的生长状况.在大自然里,有很多数学的奥秘.图1是一片美丽的心形叶片,图2是一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.
【探究一】确定心形叶片的形状
(1)如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数图象的一部分,已知图像过原点,求抛物线的解析式及顶点的坐标;
【探究二】研究心形叶片的宽度:
(2)如图3,在(1)的条件下,心形叶片的对称轴,即直线与坐标轴交于,两点,抛物线与轴交于另一点,点,是叶片上的一对对称点,交直线于点.求叶片此处的宽度;
【探究三】探究幼苗叶片的长度
(3)小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数图象的一部分;如图4,幼苗叶片下方轮廓线正好对应探究一中的二次函数.已知直线(点为叶尖)与水平线的夹角为,求幼苗叶片的长度.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B C A A B C
题号 11 12
答案 C C
1.B
【分析】根据科学记数法的方法进行解题即可.本题主要考查了用科学记数法表示较大的数,一般形式为,其中,为正整数,确定a与n的值是解题的关键.
【详解】解:依题意,数据2390000用科学记数法表示为,
故选:B
2.A
【分析】本题考查的是随机事件,必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.
【详解】解:①“水中捞月”,是不可能事件;
②“守株待兔”,是随机事件;
③“水涨船高”,是必然事件;
④“瓜熟蒂落”,是必然事件;
故选:A.
3.A
【分析】本题考查正数和负数的实际应用,若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为米,即可求解.
【详解】解:若高于海平面10米记为米,某地的高度低于海平面25米,则此处的等高线标注为米,
故选:A.
4.B
【分析】本题主要考查了反比例函数关系式,
根据工作电流与电阻成反比可得,再求出关系式,然后令求出电流,进而得出答案.
【详解】解:根据题意设反比例函数关系式为,
当时,
.
∴反比例函数关系式为,
当时,,
可知,
所以流经电阻的电流减少1A.
故选:B.
5.B
【分析】本题考查了反比例函数的性质、反比例函数图象上点的坐标特征、一次函数的应用,根据题意及反比例函数图象上点的坐标特征,逐项分析判断即可.
【详解】解:A、某位成年人身高为1.6米,数值随着体重m的值的增加而增加,原说法错误,不符合题意;
B、某位成年人身高为1.6米,数值与体重m的值之间成正比例关系,原说法正确,符合题意;
C、某位成年人身高为1.6米,数值与体重m的值之间的函数图象为第一象限内的直线,原说法错误,不符合题意;
D、某位成年人身高为1.6米,这位成年人的体重为64公斤,则数值是25,属于偏胖,原说法错误,不符合题意;
故选:B.
6.C
【分析】此题主要考查了利用频率估计概率,掌握以上知识点是解答本题的关键.
概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率.
【详解】解:因为概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率,
这种植物种子在该实验条件下发芽的概率是,
故选:C.
7.A
【分析】此题考查了解直角三角形的应用,过点D作于点E,则,证明四边形是矩形,则,,由得到,即可得到答案.
【详解】解:过点D作于点E,则,
∵,
∴四边形是矩形,
∴,
在中,,
∴
∴
故选:A
8.A
【分析】本题考查了二次函数的基本应用,直接把代入函数,解出即可得解.
【详解】解:当时,.
解得,(舍),
故这个女性的年龄为15岁,
故选:A.
9.B
【分析】本题考查函数图像,从函数图像中获取信息,逐一进行判断即可.
【详解】解:A、冰的整个熔化过程持续了;原说法正确,不符合题意;
B、第时,冰已经全部熔化,处于液体状态;原说法错误,符合题意;
C、由图像可知,冰在第时全部熔化成水;原说法正确,不符合题意;
D、由图像可知,冰的熔点是;原说法正确,不符合题意;
故选B.
10.C
【分析】本题考查了反比例函数的实际应用,根据反比例函数的性质逐一排除即可,熟练掌握反比例函数的性质是关键.
【详解】解:、设细胞的相对表面积与细胞的半径之间的函数关系式为,
当,,
∴,
∴函数关系式为,原选项正确,不符合题意;
、若细胞的相对表面积为,则细胞的半径为,原选项正确,不符合题意;
、细胞的半径每增大,相对表面积的减少量不相同,原选项错误,符合题意;
、细胞的相对表面积随着细胞半径的增大而减小,原选项正确,不符合题意;
故选:.
11.C
【分析】本题考查了反比例函数,解题的关键是理解题意,能够根据函数图象获取信息.
根据所给函数图像即可判断选项A、B,根据函数图象得与的函数关系,根据与m之间的关系得,进行计算即可判断选项C,当时,的阻值为,此时有最大值,进行计算即可判断选项D.
【详解】解:根据图 2 得,当时,的阻值为,故选项A说法正确;
在一定范围内,随的增大而减小,故选项B说法正确;
设与的函数关系为,
将代入得,
故与的函数关系为,
当托盘上货物的质量为时,令,,
则,故选项C说法错误,符合题意;
当时,的阻值为,最小,此时有最大值,即,
解得:,
即电压表量程为,为保护电压表,该电子体重秤可称的最大质量是,故选项D正确;
故选:C.
12.C
【分析】本题主要考查了反比例函数的图象与性质,熟练掌握反比例函数的图象与性质是解答本题的关键.
根据反比函数的图象与性质逐项判断即可.
【详解】A、由题图可知光敏电阻的直值随光照强度的增大雨减小,故A选项正确;
B、由题图可知图象上点的横、纵坐标之积为定值,可得,将代入反比例函数,得;
C、要使报警器在浓度更低的烟雾下报警,此时光照强度增强,由题图,可知光的电阻的阻值减小,从而控制电路的总电阻减小.因为触发投资器报警的电流不交,由,可知应减小控制电路电压,故C选项错误;
D、当光照强度为时,可知光敏电阻控制电路中的电流,故D选项正确;
故选 C.
13.100
【分析】本题是跨学科综合题.根据由等高线可知、两地的高度差为50米,然后点处测得处的俯角为求值即可.
【详解】解:由等高线可得、两地的实际高度差为,
依题意作图得:,,,
∴
故答案为:100.
14.90
【分析】本题考查待定系数法求反比例函数解析式,已知函数值求自变量值等.根据题意先设解析式为,代入得出反比例解析式,再将压强和分别代入求出自变量值再做减法即可.
【详解】解:设反比例函数解析式为:,
将代入中得:,
∴反比例解析式为:,
∴当压强为时,,
当压强为时,,
∴压强由加压到,则气体体积压缩了:,
故答案为:90.
15.25
【分析】本题考查了反比例函数的应用,根据反比例函数的图象的性质结合题意可得方程,据此可得P的值,进而得出的值,再把代入函数关系式解答即可.
【详解】解:根据题意得:,
解得,
∴,
∴,
当时,,
即当时,P的值为,
故答案为:25.
16.52
【分析】本题考查反比例函数的实际应用,求出反比例函数的解析式,求出温度上升至和下降到时的时间,进行求解即可.
【详解】解:设反比例函数的解析式为:,
由图象,把点代入,得:,
∴,
当时,,
∵刚燃烧时,落叶堆内部温度以每分钟上涨的速度匀速升高,
∴当温度上升到时,所需时间为:,
∴糖化过程时长为;
故答案为:.
17.7
【分析】本题考查待定系数法求函数解析式,一次函数图象及性质,作出点C关于对称点,可知的坐标,作直线,,分别求出这两条直线与y轴交点,则点E坐标即在范围内,即可得到整数点的个数,熟练掌握一次函数的性质是解答本题的关键.
【详解】解:如图,作点关于的对称点,则,
作直线分别交轴于,设直线的函数解析式为,
把和代入中,得,
解得,
点的坐标为.
设直线的函数解析式为,
把和代入中,得,
解得,
点的坐标为,
点纵坐标的取值范围为,
点是整点的有,共7个,
故答案为:.
18.(1)
(2)这块薄木板的面积至少.
【分析】本题考查了函数的图象,反比例函数的应用,掌握函数图象的特点是解题的关键.
()根据函数解析式即可判断求解;
()把,代入计算即可求解;
把,代入计算即可求解;
【详解】(1)解:当为定值时,是的反比例函数,故正确;
当为定值时,,是的正比例函数,故错误;
当为定值时,是的正比例函数,故正确;
∴正确的有,
故答案为:;
(2)解:把,代入
得,,
∵,
∴小明不能安全地站在这块冰面上;
把,代入得,,
解得,
∴这块薄木板的面积至少.
19.(1)
(2)王刚走了时,头顶恰好碰到这枝柳条
【分析】本题主要考查了二次函数的应用,解题时要能熟练掌握并灵活运用二次函数的性质是关键.
(1)依据题意,得该抛物线经过点和点,进而建立方程组计算可以得解;
(2)依据题意,在中,令,从而可得,求出x后即可判断得解.
【详解】(1)解:由题意知,该抛物线经过点和点,
,
解得,
该抛物线的函数表达式为.
(2)在中,令,
.
(不合题意,舍去),.
王刚走了时,头顶恰好碰到这枝柳条.
20.(1),
(2)
【分析】本题考查了二次函数和一次函数的综合应用,涉及待定系数法求解析式,二次函数的图象和性质,一次函数的图象与性质等知识点,熟练掌握二次函数和一次函数的图象与性质是解题的关键.
(1)将分别代入抛物线和直线,即可求解;
(2)先求出比火箭运行的最高点低的高度,然后代入解析式,即可求解;
【详解】(1)解:∵火箭第二级的引发点的高度为,
∴抛物线和直线均经过点,
∴,,
解得:,;
(2)解:由①知:,,
∴,
∴最大值,
当时,,
解得:,,
又∵火箭运行的水平距离为时,自动引发火箭的第二级.而火箭第二级的引发点的高度为,
∴不合题意舍去;
∴当火箭第二级高度时,在第二级则,
解得:,
∴,
∴这两个位置之间的距离为.
21.(1)
(2)①;②4;;③见解析
(3)点C的坐标为或
【分析】(1)根据公式进行计算即可;
(2)①根据公式即可得到;②根据①求出a、b的值即可;③先描点,再连线,画出函数图像即可;
(3)设,连接,,,根据三角形的面积求出a的值.
【详解】(1)解:∵,
∴,
∴重物B所受拉力为,
故答案为:;
(2)解:①∵,
∴,即,
故答案为:;
②由①得,,
填表如下:
… …
… 8 4 2 …
故答案为:4,;
③函数图象如下所示:
;
(3)解:点A的坐标为,B的坐标为,C为反比例函数上一点,
设,连接,,,
∴
,
∵,
∴,
整理得:,
解得,,
经检验,或是原方程的根,
∴时;时,,
∴点C的坐标为或.
【点睛】本题是反比例函数的综合题,主要考查了待定系数法求反比例函数的解析式,三角形的面积,反比例函数的性质和图像,正确理解题意是解题的关键.
22.(1),顶点的坐标为;(2);(3)
【分析】(1)把原点代入解析式,求得值,将抛物线化成顶点式即可确定顶点坐标;
(2)先求出点的坐标为,再求出的解析式为:.然后求出点的坐标为,最后求出结果即可;
(3)作抛物线的对称轴于点,则,设点的横坐标为,得出,根据点在抛物线上,列出方程,得出点的坐标为,最后求出即可.
【详解】解:(1)抛物线经过原点,
.
解得:.
抛物线的解析式为:.
顶点的坐标为;
(2)取,,
解得:,,
点的坐标为,
心形叶片的对称轴是直线,点,是叶片上的一对对称点,
设的解析式为:.
经过点,
.
解得:.
的解析式为:.
,
解得:
点的坐标为.
.
.
(3)作抛物线的对称轴于点,则,
直线与水平线的夹角为,
.
设点的横坐标为,
抛物线的对称轴为直线,
.
顶点的坐标为,
点的纵坐标为.
点在抛物线上,
.
解得:.
点的坐标为.
.
【点睛】本题考查了待定系数法求解析式,等腰直角三角形的判定和性质,抛物线与坐标轴的交点,对称思想,两点间的距离公式,熟练掌握待定系数法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
