人教新课标A版选修2-2数学1.3导数在研究函数中的运用同步练习
文档属性
| 名称 | 人教新课标A版选修2-2数学1.3导数在研究函数中的运用同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 848.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-15 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
1.3导数在研究函数中的运用同步练习
1. 曲线f(x)=x㏑x在点x=1处的切线方程是( )
A. y=2x+2 B.y=2x-2 C.y=x-1 D.y=x+1
答案:C
解析:解答:根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式即可解:y=xlnx, =1×ln+x =1+lnx, =1又当x=1时y=0,∴切线方程为y=x-1即x-y-1=0,故选:C
分析:此题主要考查导数的计算,以及利用导数研究曲线上某点切线方程,属于基础题
2.曲线y= 在点(1,-1)处的切线方程为
A.y=x-2 B.y=-3x+2 C.y=2x-3 D.y= -2x+1
答案:D
解析:解答:根据题意 ,由于曲线y=,则可知其导数,故当x=1时,则可知导数值为-2,则由点斜式方程可知为y= -2x+1,选D.
分析:主要是考查了导数在研究曲线的切线方程中的运用,属于基础题。
3. 函数的单调递减区间为( )
A.(-1,1] B.(0,1] C.[1,) D.(0,)
答案:B
解析:解答:根据题意,对于函数,由于(x>0),可知,当y’<0时,则可知0分析:本题考查利用导数求函数的单调区间,注意首先应求函数的定义域
4.已知f(x)=x3+x,若a,b,,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
A.一定大于0 B.一定等于0
C.一定小于0 D.正负都有可能
答案:A
解析:解答:由可知函数在定义域内为增函数,又为奇函数,则a+b>0得a>-b,,故,同理,,三式相加可得,即.
分析:此题利用函数的单调性解决不等式,有一定的技巧,属于中档题。
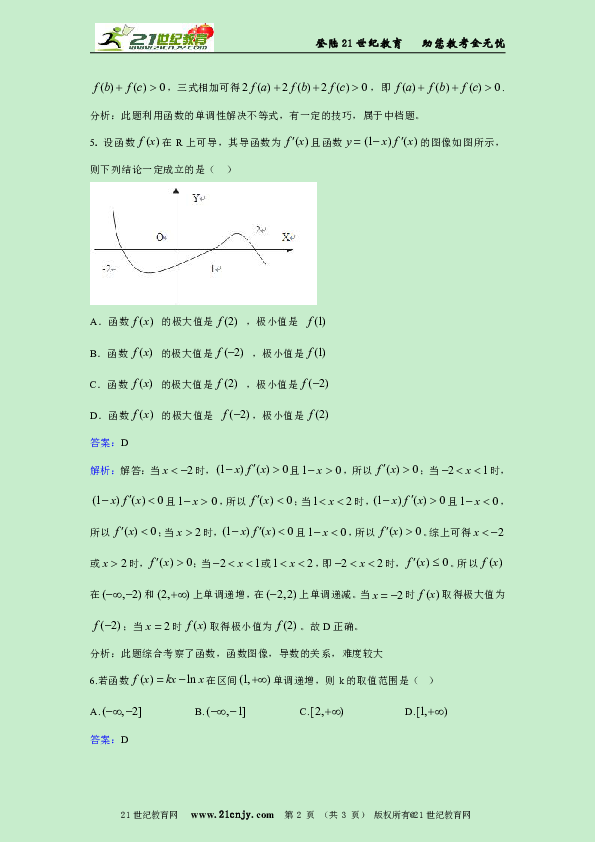
5. 设函数在R上可导,其导函数为且函数的图像如图所示,则下列结论一定成立的是( )
A.函数 的极大值是 ,极小值是
B.函数 的极大值是 ,极小值是
C.函数 的极大值是 ,极小值是
D.函数 的极大值是 ,极小值是
答案:D
解析:解答:当时,且,所以;当时,且,所以;当时,且,所以;当时,且,所以。综上可得或时,;当或,即时,。所以在和上单调递增,在上单调递减。当时取得极大值为;当时取得极小值为。故D正确。
分析:此题综合考察了函数,函数图像,导数的关系,难度较大
6.若函数在区间单调递增,则k的取值范围是( )
A. B. C. D.
答案:D
解析:解答:,由已知得在恒成立,故,因为x>1,所以,故k的取值范围是.
分析: 非常函数f(x)在区间[a,b]上递增,则导函数在区间[a,b]上有
7. 函数,则( )
A.在 上递增; B.在 上递减;
C.在 上递增; D.在 上递减
答案:D
解析:解答:因为函数,所以lnx+1, >0,解得x> ,则函数的单调递增区间为,又<0,解得0分析:非常函数f(x)在区间[a,b]上递增,则导函数在区间[a,b]上有,非常函数f(x)在区间[a,b]上递减,则导函数在区间[a,b]上有
8. 已知定义域为R的函数满足,且对任意实数x,总有
则不等式<3x-15的解集为( )
A.(﹣∞,4)
B.(﹣∞,﹣4)
C.(﹣∞,﹣4)∪(4,﹢∞)
D.(4,﹢∞)
答案:C
解析:解答:设,则所求的不等式解集可理解为使的解集.的导函数为,根据题意可知对任意实数x恒成立,所以在R上单调递减.则,令,则根据单调递减可知:.
分析: 求不等式<3x-15的解集,可以转化为求的解集,考查构造函数,难度较大
9. 函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图象如下图所示,则函数f(x)在开区间(a,b)内有极大值点的个数为()
A.1个 B.2个 C.3个 D.4个
答案:B
解析:解答:函数在点处连续且,若在点附近左侧,右侧,则点为函数的极大值点,满足定义的点有2个.
分析: 导数为0的点是函数极值的可疑点,当导函数图像从上往下穿过x轴时,为极大值点,从下往上穿过x轴时是极小值点,不穿过x轴时为驻点
10. 若函数的导函数则函数的单调递减区间是( )
A.(0,2) B.(-3,-1) C.(1,3) D.(2,4)
答案:A
解析:解答:由<0得,,所以,函数的减区间为(1,3);又函数的的图像向左平移1个单位即得到函数的图象,所以,函数的单调递减区间是(0,2),选A。
分析:简单题,在某区间,导数非负,函数为增函数,导数非正,函数为减函数。
11. 下列函数中,x=0是其极值点的是 ( ).
A.y=- B.y=cos2x
C.y=tan x-x D.y=
答案:B
解析:解答:对于B,,当x=0,,函数图像从上往下穿过x轴,所以x=0是函数的极大值点,故选B
分析:导数为0的点是函数极值的可疑点,当导函数图像从上往下穿过x轴时,为极大值点,从下往上穿过x轴时是极小值点,不穿过x轴时为驻点
12. 函数的最大值为( )
A. B.e C. D.
答案:A
解析:解答:,令,x=e,此时函数图像从上往下穿过x轴,所以x=e是函数的极大值点,在这里也是最大值点,所以最大值为,故选A
分析:f(x)在区间[a,b]上连续,则F(x)的最大值在f(x)的端点和极大值点中取到
13. 当时,不等式恒成立,则实数a的取值范围是( )
A.[-5,-3] B.[-6,1] C.[-6,-2] D. [-4,-3]
答案:C
解析:解答:不等式变形为.当x=0时,,故实数a的取值范围是R;当时,,记,,故函数递增,则,故;当时,,记,令,得x=-1或x=9(舍去),当时,;当时,,故,则.综上所述,实数a的取值范围是[-6,-2].
分析:先用分离常数法把不等式变为只含有x的式子,是此题解题的关键
14.若函数,则( )
A.最大值为1,最小值为
B.最大值为1,无最小值
C.最小值为 ,无最大值
D.既无最大值也无最小值查看解析 ( http: / / www.21cnjy.com / " \t "_blank )添 ( http: / / www.21cnjy.com / " \t "_blank )
答案:D
解析:解答:,令,得想x<0或x>1,令,得,因此函数在上单调递增,在(0,1)上单调递减,在(1,+)上单调递增,所以在x=0时,函数取得极大值1,在x=1时,函数取得极小值,但是函数在(-,+)上,既无最大值也无最小值,弄清楚极值与最值是两个不同的概念,就不会选错答案,此处选择D.
分析:弄清楚极值与最值是两个不同的概念.
15. 已知函数的图像与x轴恰有两个公共点,则c= ( )
A.-2或2 B.-9或3 C.-1或1 D.-3或1
答案:A
解析:解答:对函数进行求导即,确定函数的单调性并判断函数的极值点,即令,可得x>1或x<-1;令,可得-1分析: 利用一元三次函数图像的性质解题,难度较大
16. 曲线在点(1,3)处的切线方程为 .
答案:
解析:解答:.先求出导函数,然后x=1得,k=2,再由所求切线方程过点(1,3),所以所求切线方程为:y-3=2(x-1),化简整理得.故答案为.
分析: 函数在某一点的导数是过该点切线的斜率
17. 函数的单调递增区间是
答案:(0,e)
解析:解答: 因为, ,所以, ,0分析:简单题,在指定区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。
18. 如图是函数的导函数的图象,对此图象,有如下结论:
①在区间(-2,1)内是增函数;
②在区间(1,3)内是减函数;
③在时,取得极大值;
④在时,取得极小值。
其中正确的是 .
答案:③
解析:解答:由 的图象可知,(-3,-),,函数为减函数;所以,①在区间(-2,1)内是增函数;不正确;②在区间(1,3)内是减函数;
不正确;x=2时, =0,且在x=2的两侧导数值先正后负,③在时,取得极大值;而,x=3附近,导函数值为正,所以,④在时,取得极小值。不正确。
故答案为③。
分析:简单题,在某区间,函数的导数非负,函数为增函数,函数的导数非正,函数为减函数。
19. 函数在区间上的最大值是 .
答案:
解析:解答:对函数y=x+2cosx进行求导,研究函数在区间上的极值,本题极大值就是最大值.解:∵y=x+2cosx,∴y′=1-2sinx,令y′=0而x∈[0,]则x=当x∈[0,]时,y′>0.当x∈[,]时,y′<0.所以当x=时取极大值,也是最大值;故答案为
分析:本题考查了利用导数求闭区间上函数的最大值问题,属于导数的基础题
20. 函数在(0,1)内有极小值,则实数b的取值范围
答案:(0,1)
解析:解答:∵f(x)=x2-2bx+3a的导数为f'(x)=2x-2b,
∴f(x)极小值点是方程2x-2b=0的根,即x=b,
又∵函数f(x)在区间(0,1)内有极小值,
∴0<b<1,故答案为(0,1)
分析: 简单题,由二次函数的极小值点在指定区间内,求参数的取值范围,一般可利用导数求函数极值和二次函数的性质等求解。
21. 已知曲线y=在x=x0处的切线L经过点P(2,),求切线L的方程。
答案:解:设切于点Q(,), y'=x 2
则y-=2(x-)经过(2,)
-3+4=0 解得 =-1,或=2
∴所求的切线方程为12x-3y-16=0或3x-y+2=0
解析: 分析:函数在某一点的导数是过该点切线的斜率
22. 已知函数.
(1)试判断函数的单调性,并说明理由;
答案:解:(1)
故在递减
(2)若恒成立,求实数k的取值范围.
答案:由得 记,
再令,则
时 h(x)在上递增。
,从而 故在上也单调递增,
解析: 分析:主要是考查了函数单调性的运用,以及函数单调性与导数的符号的关系的运用,属于中档题。
23. 已知函数的图象过点P(0,2),且在点M(-1,)处的切线方程。
(1)求函数的解析式;
答案:由的图象经过点P(0,2),知d=2。
所以,则
由在处的切线方程是知,即。所以3-2b+c=6,-1+b-c+2=1解得b=c=-3。
故所求的解析式是。
(2)求函数与的图像有三个交点,求a的取值范围。
答案:因为函数g(x)与 的图像有三个交点
所以有三个根
即有三个根
令,则的图像与y=a图像有三个交点。
接下来求的极大值与极小值(表略)。的极大值为 的极小值为2
因此
解析: 分析: (1)将点P(0,2)代入函数解析式可得d的值,将代入直线可得的值,再由切线方程可知切线的斜率为6,由导数的几何意义可知即,解由和组成的方程组可得b,c的值。(2)可将问题转化为有三个不等的实根问题,将整理变形可得,令,则的图像与y=a图像有三个交点。然后对函数求导,令导数等于0求其根。讨论导数的符号,导数正得增区间,导数负得减区间,根据函数的单调性得函数的极值,数形结合分析可得出a的取值范围。
24. 已知命题p:函数在上单调递增,命题q:函数在R上是增函数.
(1)若p或q为真命题,求a的取值范围;
(2)若或为真命题,求a的取值范围.
答案:(1) ;(2)
解析:解答:解:若命题p 为真,则有 ,即 ,若命题q 为真,a>0
(1)若 为真,则,即a 的取值范围是 .
(2) 为真,则a<-2, 为真,则, 为真时,
即a的取值范围是
分析: (1)利用函数的单调性分别求出命题p和命题q所对应的集合,然后求出这两个集合的并集即可;
(2)由(1)的结果求出命题和命题所对应的集合,然后求出这两个集合的并集即可.
25. 若函数.当x=2时,函数取得极值.
(1)求函数的解析式;
答案:,所以,.即12a-b=0,8a-2b+4=,由此可解得,b=4 ∴
(2)若函数=k有3个解,求实数k的取值范围.
答案:, 所以在x=-2处取得极大值,在x=2处取得极小值 所以
解析: 分析:(1)求函数的定义域;(2)求函数的导数,令,求方程的所有实数根;(3)考察在各实数根左、右的值的符号:
①如果在x0两侧符号相同,则不是的极值点;②如果在附近的左侧,右侧,则是极大值;③如果在附近的左侧,右侧,那么是极小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 11 页 (共 11 页) 版权所有@21世纪教育网
1.3导数在研究函数中的运用同步练习
1. 曲线f(x)=x㏑x在点x=1处的切线方程是( )
A. y=2x+2 B.y=2x-2 C.y=x-1 D.y=x+1
答案:C
解析:解答:根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式即可解:y=xlnx, =1×ln+x =1+lnx, =1又当x=1时y=0,∴切线方程为y=x-1即x-y-1=0,故选:C
分析:此题主要考查导数的计算,以及利用导数研究曲线上某点切线方程,属于基础题
2.曲线y= 在点(1,-1)处的切线方程为
A.y=x-2 B.y=-3x+2 C.y=2x-3 D.y= -2x+1
答案:D
解析:解答:根据题意 ,由于曲线y=,则可知其导数,故当x=1时,则可知导数值为-2,则由点斜式方程可知为y= -2x+1,选D.
分析:主要是考查了导数在研究曲线的切线方程中的运用,属于基础题。
3. 函数的单调递减区间为( )
A.(-1,1] B.(0,1] C.[1,) D.(0,)
答案:B
解析:解答:根据题意,对于函数,由于(x>0),可知,当y’<0时,则可知0
4.已知f(x)=x3+x,若a,b,,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
A.一定大于0 B.一定等于0
C.一定小于0 D.正负都有可能
答案:A
解析:解答:由可知函数在定义域内为增函数,又为奇函数,则a+b>0得a>-b,,故,同理,,三式相加可得,即.
分析:此题利用函数的单调性解决不等式,有一定的技巧,属于中档题。
5. 设函数在R上可导,其导函数为且函数的图像如图所示,则下列结论一定成立的是( )
A.函数 的极大值是 ,极小值是
B.函数 的极大值是 ,极小值是
C.函数 的极大值是 ,极小值是
D.函数 的极大值是 ,极小值是
答案:D
解析:解答:当时,且,所以;当时,且,所以;当时,且,所以;当时,且,所以。综上可得或时,;当或,即时,。所以在和上单调递增,在上单调递减。当时取得极大值为;当时取得极小值为。故D正确。
分析:此题综合考察了函数,函数图像,导数的关系,难度较大
6.若函数在区间单调递增,则k的取值范围是( )
A. B. C. D.
答案:D
解析:解答:,由已知得在恒成立,故,因为x>1,所以,故k的取值范围是.
分析: 非常函数f(x)在区间[a,b]上递增,则导函数在区间[a,b]上有
7. 函数,则( )
A.在 上递增; B.在 上递减;
C.在 上递增; D.在 上递减
答案:D
解析:解答:因为函数,所以lnx+1, >0,解得x> ,则函数的单调递增区间为,又<0,解得0
8. 已知定义域为R的函数满足,且对任意实数x,总有
则不等式<3x-15的解集为( )
A.(﹣∞,4)
B.(﹣∞,﹣4)
C.(﹣∞,﹣4)∪(4,﹢∞)
D.(4,﹢∞)
答案:C
解析:解答:设,则所求的不等式解集可理解为使的解集.的导函数为,根据题意可知对任意实数x恒成立,所以在R上单调递减.则,令,则根据单调递减可知:.
分析: 求不等式<3x-15的解集,可以转化为求的解集,考查构造函数,难度较大
9. 函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图象如下图所示,则函数f(x)在开区间(a,b)内有极大值点的个数为()
A.1个 B.2个 C.3个 D.4个
答案:B
解析:解答:函数在点处连续且,若在点附近左侧,右侧,则点为函数的极大值点,满足定义的点有2个.
分析: 导数为0的点是函数极值的可疑点,当导函数图像从上往下穿过x轴时,为极大值点,从下往上穿过x轴时是极小值点,不穿过x轴时为驻点
10. 若函数的导函数则函数的单调递减区间是( )
A.(0,2) B.(-3,-1) C.(1,3) D.(2,4)
答案:A
解析:解答:由<0得,,所以,函数的减区间为(1,3);又函数的的图像向左平移1个单位即得到函数的图象,所以,函数的单调递减区间是(0,2),选A。
分析:简单题,在某区间,导数非负,函数为增函数,导数非正,函数为减函数。
11. 下列函数中,x=0是其极值点的是 ( ).
A.y=- B.y=cos2x
C.y=tan x-x D.y=
答案:B
解析:解答:对于B,,当x=0,,函数图像从上往下穿过x轴,所以x=0是函数的极大值点,故选B
分析:导数为0的点是函数极值的可疑点,当导函数图像从上往下穿过x轴时,为极大值点,从下往上穿过x轴时是极小值点,不穿过x轴时为驻点
12. 函数的最大值为( )
A. B.e C. D.
答案:A
解析:解答:,令,x=e,此时函数图像从上往下穿过x轴,所以x=e是函数的极大值点,在这里也是最大值点,所以最大值为,故选A
分析:f(x)在区间[a,b]上连续,则F(x)的最大值在f(x)的端点和极大值点中取到
13. 当时,不等式恒成立,则实数a的取值范围是( )
A.[-5,-3] B.[-6,1] C.[-6,-2] D. [-4,-3]
答案:C
解析:解答:不等式变形为.当x=0时,,故实数a的取值范围是R;当时,,记,,故函数递增,则,故;当时,,记,令,得x=-1或x=9(舍去),当时,;当时,,故,则.综上所述,实数a的取值范围是[-6,-2].
分析:先用分离常数法把不等式变为只含有x的式子,是此题解题的关键
14.若函数,则( )
A.最大值为1,最小值为
B.最大值为1,无最小值
C.最小值为 ,无最大值
D.既无最大值也无最小值查看解析 ( http: / / www.21cnjy.com / " \t "_blank )添 ( http: / / www.21cnjy.com / " \t "_blank )
答案:D
解析:解答:,令,得想x<0或x>1,令,得,因此函数在上单调递增,在(0,1)上单调递减,在(1,+)上单调递增,所以在x=0时,函数取得极大值1,在x=1时,函数取得极小值,但是函数在(-,+)上,既无最大值也无最小值,弄清楚极值与最值是两个不同的概念,就不会选错答案,此处选择D.
分析:弄清楚极值与最值是两个不同的概念.
15. 已知函数的图像与x轴恰有两个公共点,则c= ( )
A.-2或2 B.-9或3 C.-1或1 D.-3或1
答案:A
解析:解答:对函数进行求导即,确定函数的单调性并判断函数的极值点,即令,可得x>1或x<-1;令,可得-1
16. 曲线在点(1,3)处的切线方程为 .
答案:
解析:解答:.先求出导函数,然后x=1得,k=2,再由所求切线方程过点(1,3),所以所求切线方程为:y-3=2(x-1),化简整理得.故答案为.
分析: 函数在某一点的导数是过该点切线的斜率
17. 函数的单调递增区间是
答案:(0,e)
解析:解答: 因为, ,所以, ,0
18. 如图是函数的导函数的图象,对此图象,有如下结论:
①在区间(-2,1)内是增函数;
②在区间(1,3)内是减函数;
③在时,取得极大值;
④在时,取得极小值。
其中正确的是 .
答案:③
解析:解答:由 的图象可知,(-3,-),,函数为减函数;所以,①在区间(-2,1)内是增函数;不正确;②在区间(1,3)内是减函数;
不正确;x=2时, =0,且在x=2的两侧导数值先正后负,③在时,取得极大值;而,x=3附近,导函数值为正,所以,④在时,取得极小值。不正确。
故答案为③。
分析:简单题,在某区间,函数的导数非负,函数为增函数,函数的导数非正,函数为减函数。
19. 函数在区间上的最大值是 .
答案:
解析:解答:对函数y=x+2cosx进行求导,研究函数在区间上的极值,本题极大值就是最大值.解:∵y=x+2cosx,∴y′=1-2sinx,令y′=0而x∈[0,]则x=当x∈[0,]时,y′>0.当x∈[,]时,y′<0.所以当x=时取极大值,也是最大值;故答案为
分析:本题考查了利用导数求闭区间上函数的最大值问题,属于导数的基础题
20. 函数在(0,1)内有极小值,则实数b的取值范围
答案:(0,1)
解析:解答:∵f(x)=x2-2bx+3a的导数为f'(x)=2x-2b,
∴f(x)极小值点是方程2x-2b=0的根,即x=b,
又∵函数f(x)在区间(0,1)内有极小值,
∴0<b<1,故答案为(0,1)
分析: 简单题,由二次函数的极小值点在指定区间内,求参数的取值范围,一般可利用导数求函数极值和二次函数的性质等求解。
21. 已知曲线y=在x=x0处的切线L经过点P(2,),求切线L的方程。
答案:解:设切于点Q(,), y'=x 2
则y-=2(x-)经过(2,)
-3+4=0 解得 =-1,或=2
∴所求的切线方程为12x-3y-16=0或3x-y+2=0
解析: 分析:函数在某一点的导数是过该点切线的斜率
22. 已知函数.
(1)试判断函数的单调性,并说明理由;
答案:解:(1)
故在递减
(2)若恒成立,求实数k的取值范围.
答案:由得 记,
再令,则
时 h(x)在上递增。
,从而 故在上也单调递增,
解析: 分析:主要是考查了函数单调性的运用,以及函数单调性与导数的符号的关系的运用,属于中档题。
23. 已知函数的图象过点P(0,2),且在点M(-1,)处的切线方程。
(1)求函数的解析式;
答案:由的图象经过点P(0,2),知d=2。
所以,则
由在处的切线方程是知,即。所以3-2b+c=6,-1+b-c+2=1解得b=c=-3。
故所求的解析式是。
(2)求函数与的图像有三个交点,求a的取值范围。
答案:因为函数g(x)与 的图像有三个交点
所以有三个根
即有三个根
令,则的图像与y=a图像有三个交点。
接下来求的极大值与极小值(表略)。的极大值为 的极小值为2
因此
解析: 分析: (1)将点P(0,2)代入函数解析式可得d的值,将代入直线可得的值,再由切线方程可知切线的斜率为6,由导数的几何意义可知即,解由和组成的方程组可得b,c的值。(2)可将问题转化为有三个不等的实根问题,将整理变形可得,令,则的图像与y=a图像有三个交点。然后对函数求导,令导数等于0求其根。讨论导数的符号,导数正得增区间,导数负得减区间,根据函数的单调性得函数的极值,数形结合分析可得出a的取值范围。
24. 已知命题p:函数在上单调递增,命题q:函数在R上是增函数.
(1)若p或q为真命题,求a的取值范围;
(2)若或为真命题,求a的取值范围.
答案:(1) ;(2)
解析:解答:解:若命题p 为真,则有 ,即 ,若命题q 为真,a>0
(1)若 为真,则,即a 的取值范围是 .
(2) 为真,则a<-2, 为真,则, 为真时,
即a的取值范围是
分析: (1)利用函数的单调性分别求出命题p和命题q所对应的集合,然后求出这两个集合的并集即可;
(2)由(1)的结果求出命题和命题所对应的集合,然后求出这两个集合的并集即可.
25. 若函数.当x=2时,函数取得极值.
(1)求函数的解析式;
答案:,所以,.即12a-b=0,8a-2b+4=,由此可解得,b=4 ∴
(2)若函数=k有3个解,求实数k的取值范围.
答案:, 所以在x=-2处取得极大值,在x=2处取得极小值 所以
解析: 分析:(1)求函数的定义域;(2)求函数的导数,令,求方程的所有实数根;(3)考察在各实数根左、右的值的符号:
①如果在x0两侧符号相同,则不是的极值点;②如果在附近的左侧,右侧,则是极大值;③如果在附近的左侧,右侧,那么是极小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 11 页 (共 11 页) 版权所有@21世纪教育网
