22.3实际问题与二次函数——应用题常见题型集中训练(含简单答案) 人教版数学九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数——应用题常见题型集中训练(含简单答案) 人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 160.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 20:42:13 | ||
图片预览



文档简介
22.3实际问题与二次函数——应用题常见题型集中训练
1.为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为每个40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(个)与销售单价x(元)满足一次函数关系:.
(1)求出利润S(元)与销售单价x(元)之间的关系式(利润销售额成本);
(2)该公司当地物价部门规定,商品售价不得高于成本的倍,当销售单价定为多少时,该公司每天获取的利润最大 最大利润是多少元
2.从2020年开始,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量(件)与销售单价(元)满足,设销售这种商品每天的利润为(元).
(1)求与之间的函数关系式(不必写出自变量的取值范围);
(2)该商家每天想获得1250元的利润,又要减少库存,应将销售单价定为多少元?
(3)若销售单价不低于28元,且每天至少销售50件时,求的最大值.
3.“三只羊”是我市某直播平台,近年,销售额频频突破百亿大关.某坚果公司在“三只羊”直播平台中推出一款“新春”产品礼盒,每盒的成本为元,若按每盒元销售,则同时段每天可售出盒.为了新年回馈网友,公司决定降价销售.经核算,发现销售价每降低1元,同时段每天的销量就增加盒.设该礼盒售价为每盒x元(),同时段每天的销售量为y盒,每天的销售利润为w元.
(1)写出y与x的函数表达式(含自变量x的取值范围);
(2)直播间在让利顾客的前提下,要使1天的销售利润达到元,销售价应定为每盒多少元?
(3)当销售价定为多少元时每天的利润最大?并求出最大利润.
4.中国传统手工艺品,如中国结、油纸伞、团扇等,是先民智慧和勤劳的结晶,是中华传统文化的表达方式之一,也是各地传统风俗的体现.某工艺品店购进一批团扇,每把进价为20元,按每把25元销售,每月可售出210把.现店方想采用提高售价的方法来增加利润(售价不超过32元).经试验,每把团扇的售价每提高1元,每月就会少卖出10把.
(1)求每月团扇的销售量y(把)与每把售价x(元)之间的函数关系式.
(2)当每把团扇的售价定为多少时,每月的销售利润w(元)最大?最大利润为多少?
5.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为元,每日销售量()与销售单价(元)满足一次函数关系.下表记录的是有关数据.经销售发现,销售单价不低于成本价且不高于元.设公司销售板栗的日获利为(元).
(元)
()
(1)求日销售量与销售单价之间的函数关系式.(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
6.某幢建筑物,从米高的窗口用水管向外喷水(米),喷的水流呈抛物线(抛物线所在平面与墙面垂直),如图,如果抛物线的最高点离墙米,离地面米,求水流落地点到墙的距离.
7.每年10月至12月是永兴冰糖橙上市的最好季节.某果园2021年的冰糖橙销量为3万千克,2023年销量为万千克,已知每年销量增长率a相等.
(1)求销量增长率a;
(2)某水果商以90元/箱从果园进货,再以100元/箱卖出,每周可以卖出100箱.该水果商想涨价销售,每箱每涨价1元,每周销量减少4箱.设每周销售冰糖橙获利W元,每箱涨价x元(水果商每周至少卖出80箱).写出W(元)与涨价x(元/箱)之间的函数关系式;求出水果商每周销售冰糖橙利润W的最大值.
8.“香梨”是新疆特产水果,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?最高是多少元?
9.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元 如果能,求出此时的销售价格;如果不能,请说明理由.
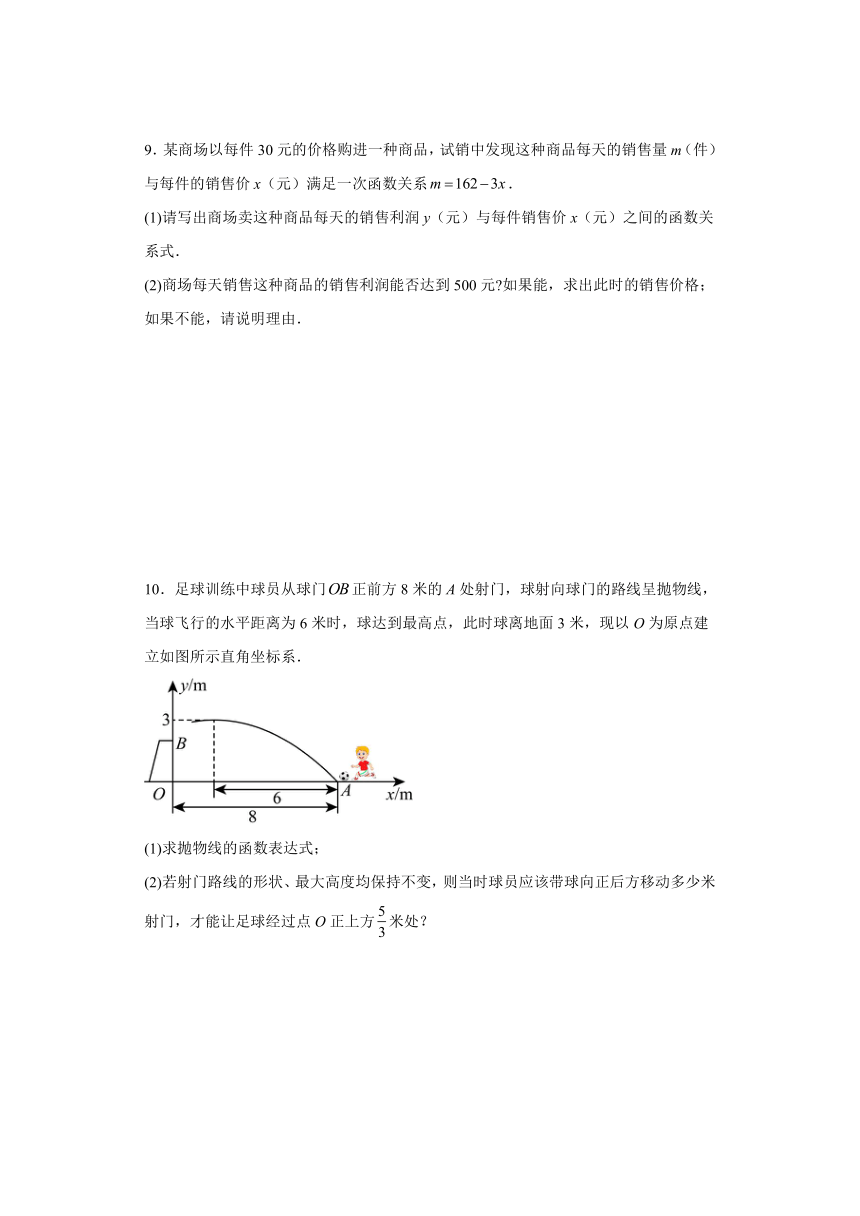
10.足球训练中球员从球门正前方8米的A处射门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)若射门路线的形状、最大高度均保持不变,则当时球员应该带球向正后方移动多少米射门,才能让足球经过点O正上方米处?
11.某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)]
销售单价x(元) 75 78 82
日销售量y(件) 150 120 80
日销售利润w(元) 5250 a 3360
(1)根据以上信息,求y关于x的函数关系式;
(2)①填空:该产品的成本单价是 元,表中a的值是 .
②求该商品日销售利润的最大值.
(3)由于某种原因,该商品进价降低了m元/件,该商店在今后的销售中,商店规定该商品的销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,若日销售最大利润是6600元,求m的值.
12.某商场销售一种成本为每件20元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500.
(1)设商场销售该种商品每月获得利润为w(元),写出w与x之间的函数关系式;
(2)如果商场想要销售该种商品每月获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该种商品,商场若销售新产品,每月销售量与销售价格之间的关系与原产品的销售情况相同,新产品为每件22元,同时对商场的销售量每月不小于150件的商场,政府部门给予每件3元的补贴,试求定价多少时,新产品每月可获得销售利润最大?并求最大利润.
13.某批发商以每件50元的价格购进500件T恤,若以单价70元销售,预计可售出200件,批发商的销售策略是:第一个月为增加销售,在单价70元的基础上降价销售,经过市场调查,单价每降低1元,可多售出10件,但最低单价高于购进的价格,每一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.
(1)若设第一个月单价降低x元,当月出售T恤获得的利润为y1元,清仓剩余T恤获得的利润为y2元,请分别求出y1、y2与x的函数关系式;
(2)从增加销售量的角度看,第一个月批发商降价多少元时,销售完这批T恤获得的利润为1000元?
(3)按照批发商的销售策略,销售完这批T恤有可能亏本吗?请说明理由.(参考数据:≈2.23)
14.某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个;定价每增加1元,销售量将减少10个.
(1)设销售定价为x元,销售量为y个,用含x的代数式表示y;
(2)若商店准备获利2000元,则销售定价为多少元?商店应进货多少个?
(3)若商店要获得最大利润,则销售定价为多少元?商店应进货多少个?
15.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元?
参考答案:
1.(1)
(2)当销售单价最大为76时,利润最大为15840元
2.(1);
(2)为了减少库存,将销售单价应定为15元;
(3)此时的最大值为2160元.
3.(1)()
(2)元
(3)销售价定为元时每天的利润最大,最大利润为
4.(1)
(2)每把团扇的售价定为32元时,每月的销售利润最大,最大利润为1680元
5.(1)
(2)当销售单价定为元时,销售这种板栗日获利最大,最大利润为元
6.水流落地点到墙的距离为米
7.(1)销量增长率为
(2);利润W的最大值为1225元
8.(1)每箱产品应涨价元
(2)每箱产品应涨价元才能获利最高,最高是元
9.(1)
(2)不能
10.(1)
(2)当时球员应该带球向正后方移动2米射门,才能让足球经过点O正上方米处
11.(1)一次函数解析式为;
(2)①40,4560;②该商品日销售利润的最大值为6250元;
(3)的值为2.
12.(1)w=﹣10x2+700x﹣10000,
(2)想要每月获得2000元的利润,每月成本至少2000元.
(3)当定价34.5元时,新产品每月可获得销售利润最大值是2402.5元.
13.(1)y1=﹣10x2+4000,(0<x<20);y2=100x﹣3000,(0<x<20);(2)10元;(3)有可能亏本
14.(1)、y=700-10x;(2)、销售定价为50元,进货200个或销售定价为60元,进货100个商店都能获利2000元;(3)、销售价应定为55元,应进货150个.
15.(1)一次函数的关系式为y=﹣x+40;
(2)产品的销售价应定为25元,此时每日的销售利润为225元.
1.为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为每个40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(个)与销售单价x(元)满足一次函数关系:.
(1)求出利润S(元)与销售单价x(元)之间的关系式(利润销售额成本);
(2)该公司当地物价部门规定,商品售价不得高于成本的倍,当销售单价定为多少时,该公司每天获取的利润最大 最大利润是多少元
2.从2020年开始,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量(件)与销售单价(元)满足,设销售这种商品每天的利润为(元).
(1)求与之间的函数关系式(不必写出自变量的取值范围);
(2)该商家每天想获得1250元的利润,又要减少库存,应将销售单价定为多少元?
(3)若销售单价不低于28元,且每天至少销售50件时,求的最大值.
3.“三只羊”是我市某直播平台,近年,销售额频频突破百亿大关.某坚果公司在“三只羊”直播平台中推出一款“新春”产品礼盒,每盒的成本为元,若按每盒元销售,则同时段每天可售出盒.为了新年回馈网友,公司决定降价销售.经核算,发现销售价每降低1元,同时段每天的销量就增加盒.设该礼盒售价为每盒x元(),同时段每天的销售量为y盒,每天的销售利润为w元.
(1)写出y与x的函数表达式(含自变量x的取值范围);
(2)直播间在让利顾客的前提下,要使1天的销售利润达到元,销售价应定为每盒多少元?
(3)当销售价定为多少元时每天的利润最大?并求出最大利润.
4.中国传统手工艺品,如中国结、油纸伞、团扇等,是先民智慧和勤劳的结晶,是中华传统文化的表达方式之一,也是各地传统风俗的体现.某工艺品店购进一批团扇,每把进价为20元,按每把25元销售,每月可售出210把.现店方想采用提高售价的方法来增加利润(售价不超过32元).经试验,每把团扇的售价每提高1元,每月就会少卖出10把.
(1)求每月团扇的销售量y(把)与每把售价x(元)之间的函数关系式.
(2)当每把团扇的售价定为多少时,每月的销售利润w(元)最大?最大利润为多少?
5.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为元,每日销售量()与销售单价(元)满足一次函数关系.下表记录的是有关数据.经销售发现,销售单价不低于成本价且不高于元.设公司销售板栗的日获利为(元).
(元)
()
(1)求日销售量与销售单价之间的函数关系式.(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
6.某幢建筑物,从米高的窗口用水管向外喷水(米),喷的水流呈抛物线(抛物线所在平面与墙面垂直),如图,如果抛物线的最高点离墙米,离地面米,求水流落地点到墙的距离.
7.每年10月至12月是永兴冰糖橙上市的最好季节.某果园2021年的冰糖橙销量为3万千克,2023年销量为万千克,已知每年销量增长率a相等.
(1)求销量增长率a;
(2)某水果商以90元/箱从果园进货,再以100元/箱卖出,每周可以卖出100箱.该水果商想涨价销售,每箱每涨价1元,每周销量减少4箱.设每周销售冰糖橙获利W元,每箱涨价x元(水果商每周至少卖出80箱).写出W(元)与涨价x(元/箱)之间的函数关系式;求出水果商每周销售冰糖橙利润W的最大值.
8.“香梨”是新疆特产水果,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?最高是多少元?
9.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元 如果能,求出此时的销售价格;如果不能,请说明理由.
10.足球训练中球员从球门正前方8米的A处射门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)若射门路线的形状、最大高度均保持不变,则当时球员应该带球向正后方移动多少米射门,才能让足球经过点O正上方米处?
11.某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)]
销售单价x(元) 75 78 82
日销售量y(件) 150 120 80
日销售利润w(元) 5250 a 3360
(1)根据以上信息,求y关于x的函数关系式;
(2)①填空:该产品的成本单价是 元,表中a的值是 .
②求该商品日销售利润的最大值.
(3)由于某种原因,该商品进价降低了m元/件,该商店在今后的销售中,商店规定该商品的销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,若日销售最大利润是6600元,求m的值.
12.某商场销售一种成本为每件20元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500.
(1)设商场销售该种商品每月获得利润为w(元),写出w与x之间的函数关系式;
(2)如果商场想要销售该种商品每月获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该种商品,商场若销售新产品,每月销售量与销售价格之间的关系与原产品的销售情况相同,新产品为每件22元,同时对商场的销售量每月不小于150件的商场,政府部门给予每件3元的补贴,试求定价多少时,新产品每月可获得销售利润最大?并求最大利润.
13.某批发商以每件50元的价格购进500件T恤,若以单价70元销售,预计可售出200件,批发商的销售策略是:第一个月为增加销售,在单价70元的基础上降价销售,经过市场调查,单价每降低1元,可多售出10件,但最低单价高于购进的价格,每一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.
(1)若设第一个月单价降低x元,当月出售T恤获得的利润为y1元,清仓剩余T恤获得的利润为y2元,请分别求出y1、y2与x的函数关系式;
(2)从增加销售量的角度看,第一个月批发商降价多少元时,销售完这批T恤获得的利润为1000元?
(3)按照批发商的销售策略,销售完这批T恤有可能亏本吗?请说明理由.(参考数据:≈2.23)
14.某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个;定价每增加1元,销售量将减少10个.
(1)设销售定价为x元,销售量为y个,用含x的代数式表示y;
(2)若商店准备获利2000元,则销售定价为多少元?商店应进货多少个?
(3)若商店要获得最大利润,则销售定价为多少元?商店应进货多少个?
15.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元?
参考答案:
1.(1)
(2)当销售单价最大为76时,利润最大为15840元
2.(1);
(2)为了减少库存,将销售单价应定为15元;
(3)此时的最大值为2160元.
3.(1)()
(2)元
(3)销售价定为元时每天的利润最大,最大利润为
4.(1)
(2)每把团扇的售价定为32元时,每月的销售利润最大,最大利润为1680元
5.(1)
(2)当销售单价定为元时,销售这种板栗日获利最大,最大利润为元
6.水流落地点到墙的距离为米
7.(1)销量增长率为
(2);利润W的最大值为1225元
8.(1)每箱产品应涨价元
(2)每箱产品应涨价元才能获利最高,最高是元
9.(1)
(2)不能
10.(1)
(2)当时球员应该带球向正后方移动2米射门,才能让足球经过点O正上方米处
11.(1)一次函数解析式为;
(2)①40,4560;②该商品日销售利润的最大值为6250元;
(3)的值为2.
12.(1)w=﹣10x2+700x﹣10000,
(2)想要每月获得2000元的利润,每月成本至少2000元.
(3)当定价34.5元时,新产品每月可获得销售利润最大值是2402.5元.
13.(1)y1=﹣10x2+4000,(0<x<20);y2=100x﹣3000,(0<x<20);(2)10元;(3)有可能亏本
14.(1)、y=700-10x;(2)、销售定价为50元,进货200个或销售定价为60元,进货100个商店都能获利2000元;(3)、销售价应定为55元,应进货150个.
15.(1)一次函数的关系式为y=﹣x+40;
(2)产品的销售价应定为25元,此时每日的销售利润为225元.
同课章节目录
