第14章 统计 单元练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 第14章 统计 单元练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 197.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-15 09:54:26 | ||
图片预览


文档简介
第14章 统计
本 章 复 习
一、 单项选择题
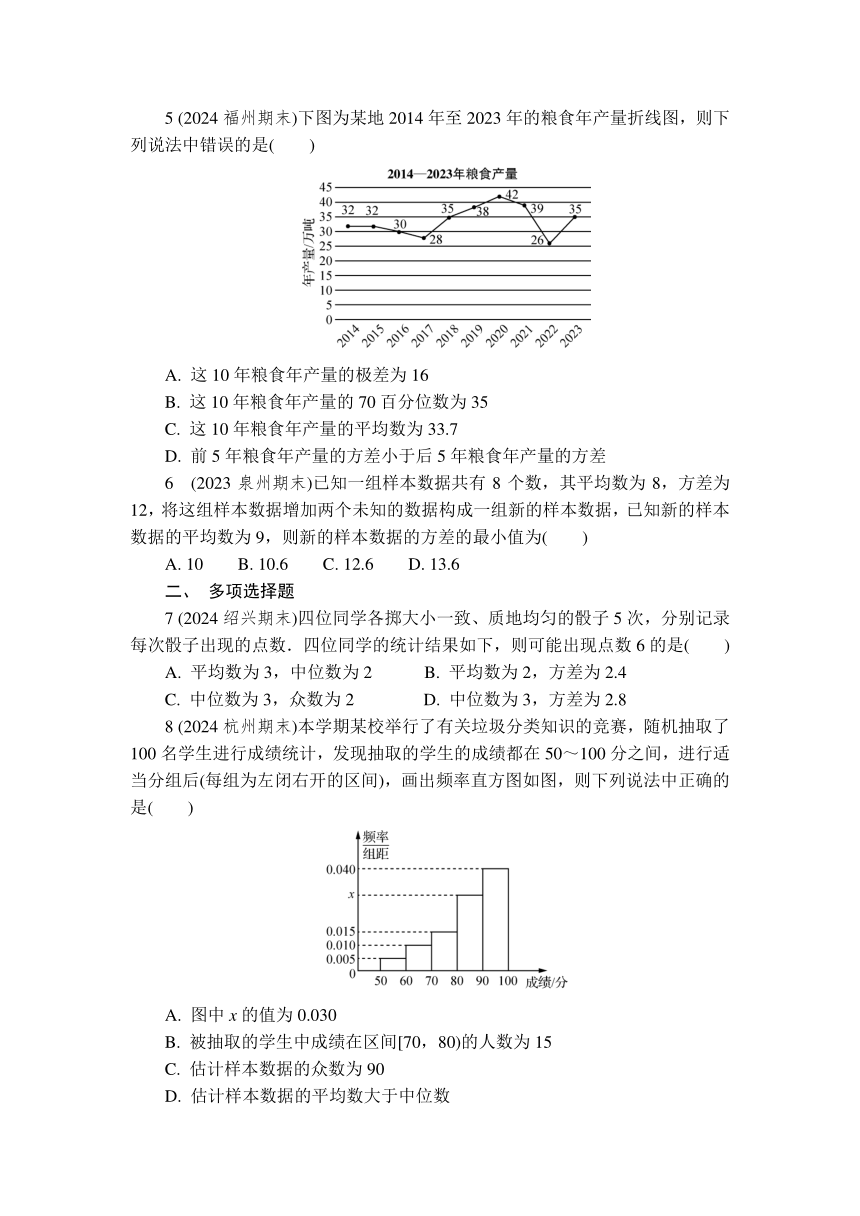
1 嫦娥五号的成功发射,实现了中国航天史上的五个“首次”.某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为01,02,…,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第6个个体的编号为( )
45 67 32 12 12 31 02 01 04 52 15 20 01 12 51 29
32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A. 12 B. 20 C. 29 D. 23
2 (2024衢州期末)将10个数据按照从小到大的顺序排列如下:11,15,17,a,23,26,27,34,37,38,若该组数据的40百分位数为22,则a的值为( )
A. 19 B. 20 C. 21 D. 22
3 (2024连云港期末)根据《中华人民共和国道路交通安全法》规定:血液酒精浓度在80 mg/100 ml(含80)以上时,属醉酒驾车,处十五日以下拘留和三个月以上六个月以下暂扣驾驶证,并处500元以上2 000元以下罚款.2024年3月以来,某地区交警查处酒后驾车和醉酒驾车共20人.如图,这是对这20人酒后驾车血液中酒精含量进行检测所得结果的频率直方图,则在这20人中属于醉酒驾车的人数约为( )
A. 1 B. 2 C. 3 D. 4
4 (2024湖州期末)如图所示的频率直方图呈现右拖尾形态,则根据此图作出判断,下列结论中正确的是( )
A. 众数<中位数<平均数
B. 众数<平均数<中位数
C. 中位数<平均数<众数
D. 中位数<众数<平均数
5 (2024福州期末)下图为某地2014年至2023年的粮食年产量折线图,则下列说法中错误的是( )
A. 这10年粮食年产量的极差为16
B. 这10年粮食年产量的70百分位数为35
C. 这10年粮食年产量的平均数为33.7
D. 前5年粮食年产量的方差小于后5年粮食年产量的方差
6 (2023泉州期末)已知一组样本数据共有8个数,其平均数为8,方差为12,将这组样本数据增加两个未知的数据构成一组新的样本数据,已知新的样本数据的平均数为9,则新的样本数据的方差的最小值为( )
A. 10 B. 10.6 C. 12.6 D. 13.6
二、 多项选择题
7 (2024绍兴期末)四位同学各掷大小一致、质地均匀的骰子5次,分别记录每次骰子出现的点数.四位同学的统计结果如下,则可能出现点数6的是( )
A. 平均数为3,中位数为2 B. 平均数为2,方差为2.4
C. 中位数为3,众数为2 D. 中位数为3,方差为2.8
8 (2024杭州期末)本学期某校举行了有关垃圾分类知识的竞赛,随机抽取了100名学生进行成绩统计,发现抽取的学生的成绩都在50~100分之间,进行适当分组后(每组为左闭右开的区间),画出频率直方图如图,则下列说法中正确的是( )
A. 图中x的值为0.030
B. 被抽取的学生中成绩在区间[70,80)的人数为15
C. 估计样本数据的众数为90
D. 估计样本数据的平均数大于中位数
三、 填空题
9 某学校高中三个年级共有团干部56名,现采用分层抽样的方法从中抽取7人进行睡眠时间调查,其中从高一年级抽取了3人,则高一年级团干部的人数为________.
10 (2024温州期末)已知样本数据x1,x2,…,x9的平均数为9,方差为12,现这组样本数据增加一个数据x10,此时新样本数据的平均数为10,则新样本数据的方差为________.
11 2022年第24届冬奥会在北京、延庆和张家口成功举办,出色的赛事组织工作赢得了国际社会的一致称赞.经济效益方面,多项收入也创下历届冬奥会新高.某机构对本届冬奥会各项主要收入进行了统计,得到的数据如图所示.已知赛事转播的收入比政府补贴和特许商品销售的收入之和多27亿元,则估计2022年冬奥会这几项收入总和约为________亿元.(结果保留整数)
四、 解答题
12 (2024河北期末)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1) 求频率直方图中a的值;
(2) 已知该市有30万居民,估计全市居民中月均用水量不低于3 t的人数,并说明理由;
(3) 估计居民月均用水量的众数、中位数.
13 (2023信阳期末)信阳市旅游部门为了促进信阳生态特色城镇和新农村建设,将甲、乙、丙三家民宿的相关资料放到某网络平台上进行推广宣传. 该平台邀请部分曾在这三家民宿体验过的游客参与调查,得到了这三家民宿的“综合满意度”评分,评分越高表明游客体验越好,现从这三家民宿“综合满意度”的评分中各随机抽取10个评分数据,并对所得数据进行整理、描述和分析,下面给出了部分信息.
①甲、乙两家民宿“综合满意度”评分的折线图:
②丙家民宿“综合满意度”评分:
2.6,4.7,4.5,5.0,4.5,4.8,4.5,3.8,4.5,3.1
③甲、乙、丙三家民宿“综合满意度”评分的平均数、中位数:
甲 乙 丙
平均数 m 4.5 4.2
中位数 4.5 4.7 n
根据以上信息,回答下列问题:
(1) 表中m的值是________,n的值是________;
(2) 设甲、乙、丙三家民宿“综合满意度”评分的方差分别为s,s,s,试比较其大小;
(3) 根据“综合满意度”的评分情况,该平台打算将甲、乙、丙三家民宿中的一家置顶推荐,你认为该平台会将这三家民宿中的哪家置顶推荐?请说明理由(至少从两个方面说明).
第14章 统 计
本 章 复 习
1. B 依次从数表中读出的有效编号为12,02,01,04,15,20,得到选出来的第6个个体的编号为20.
2. C 40%×10=4,又该组数据的40百分位数为22,则=22,解得a=21.
3. C 由频率直方图可知酒精浓度在80 mg/100 mL(含80)以上的频率为(0.01+0.005)×10=0.15,所以样本中属于醉酒驾车的人数约为20×0.15=3.
4. A 由频率直方图可知数据组的众数为左起第2个小矩形下底边中点值,显然在过该中点垂直于横轴的直线及左侧的矩形面积和小于0.5,则众数<中位数.由频率直方图呈现右拖尾形态,得中位数<平均数,所以众数<中位数<平均数.
5. B 对于A,将样本数据从小到大排列为26,28,30,32,32,35,35,38,39,42,这10年的粮食年产量的极差为42-26=16,故A正确;对于B,10×70%=7,结合A选项可知70百分位数为第7个数和第8个数的平均数,即=36.5,故B不正确;对于C,这10年粮食年产量的平均数为×(32+32+30+28+35+38+42+39+26+35)=33.7,故C正确;对于D,结合折线图可知前5年的粮食年产量的波动小于后5年的粮食年产量波动,所以前5年的粮食年产量的方差小于后5年的粮食年产量的方差,故D正确.
6. D 设增加的数为x,y,原来的8个数分别为a1,a2,…,a8,则a1+a2+…+a8=64,a1+a2+…+a8+x+y=90,所以x+y=26.又(ai-8)2=12,即(ai-8)2=96,所以新的样本数据的方差为[(ai-9)2+(x-9)2+(y-9)2]=[(ai-8)2-2(ai-8)+8+(x-9)2+(y-9)2]=(x2+y2-202).因为≥=13,所以x2+y2-202≥136,所以方差的最小值为13.6,当且仅当x=y=13时取到最小值.
7. ACD 对于A,当掷骰子出现的结果为1,1,2,5,6时,满足平均数为3,中位数为2,可以出现点6,故A正确;对于B,若平均数为2,且出现点数6,则方差s2>(6-2)2=3.2>2.4,所以当平均数为2,方差为2.4时,一定不会出现点数6,故B错误;对于C,当掷骰子出现的结果为2,2,3,4,6时,满足中位数为3,众数为2,可以出现点6,故C正确;对于D,当掷骰子出现的结果为1,2,3,3,6时,满足中位数为3,则平均数为=(1+2+3+3+6)=3,方差为s2=[(1-3)2+(2-3)2+(3-3)2+(3-3)2+(6-3)2]=2.8,所以可以出现点6,故D正确.故选ACD.
8. AB 对于A,结合频率直方图的性质可得(0.005+0.01+0.015+x+0.04)×10=1,解得x=0.03,故A正确;对于B,成绩在区间[70,80)的频率为0.015×10=0.15,人数为100×0.15=15,故B正确;对于C,众数为=95,故C错误;对于D,平均成绩为55×0.05+65×0.1+75×0.15+85×0.3+95×0.4=84,低于80分的频率为0.05+0.1+0.15=0.3,设样本数据的中位数为n,则(n-80)×0.030=0.2,解得n≈86.7,平均数小于中位数,故D错误.故选AB.
9. 24 高一年级团干部的人数为56×=24.
10. 19.8 设增加的数为k,则x1+x2+…+x9=81,x1+x2+…+x9+k=100,所以k=19,又因为(xi-9)2=12,即(xi-9)2=108,所以[ (xi-10)2+(k-10)2]=[ (xi-9)2-2(xi-9)+9+81]=19.8.
11. 218 设收入总和为x,则35.4%x-(12.2%+10.8%)x=27,解得x≈218.
12. (1) 由频率直方图知(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,解得a=0.30,
所以频率直方图中a的值为0.30.
(2) 由图得月均用水量不低于3 t的频率为0.5×(0.12+0.08+0.04)=0.12,
所以估计全市居民中月均用水量不低于3 t的人数为300 000×0.12=36 000.
(3) 由图可知众数是=2.25(t).
因为(0.08+0.16+0.30+0.42)×0.5=0.48<0.5,(0.08+0.16+0.30+0.42+0.50)×0.5=0.73>0.5,
所以中位数在区间[2,2.5)上,设中位数为x,
则0.48+0.50(x-2)=0.5,解得x=2.04,
即中位数为2.04 t.
13. (1) 4.5 4.5 甲家民宿“综合满意度”评分为3.2,4.2,5.0,4.5,5.0,4.8,4.5,4.3,5.0,4.5,所以m=×(3.2+4.2+5.0+4.5+5.0+4.8+4.5+4.3+5.0+4.5)=4.5.因为丙家民宿“综合满意度”评分为2.6,4.7,4.5,5.0,4.5,4.8,4.5,3.8,4.5,3.1,从小到大排列为2.6,3.1,3.8,4.5,4.5,4.5,4.5,4.7,4.8,5.0,所以中位数n==4.5.
(2) 根据折线统计图可知乙的评分数据在4分与5分之间波动,甲的数据在3.2分和5分之间波动,丙的数据在2.6分至5分之间波动,所以s(3) 推荐乙,理由如下:乙的方差最小,数据稳定,平均分比丙高.(答案不唯一,合理即可)
本 章 复 习
一、 单项选择题
1 嫦娥五号的成功发射,实现了中国航天史上的五个“首次”.某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为01,02,…,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第6个个体的编号为( )
45 67 32 12 12 31 02 01 04 52 15 20 01 12 51 29
32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A. 12 B. 20 C. 29 D. 23
2 (2024衢州期末)将10个数据按照从小到大的顺序排列如下:11,15,17,a,23,26,27,34,37,38,若该组数据的40百分位数为22,则a的值为( )
A. 19 B. 20 C. 21 D. 22
3 (2024连云港期末)根据《中华人民共和国道路交通安全法》规定:血液酒精浓度在80 mg/100 ml(含80)以上时,属醉酒驾车,处十五日以下拘留和三个月以上六个月以下暂扣驾驶证,并处500元以上2 000元以下罚款.2024年3月以来,某地区交警查处酒后驾车和醉酒驾车共20人.如图,这是对这20人酒后驾车血液中酒精含量进行检测所得结果的频率直方图,则在这20人中属于醉酒驾车的人数约为( )
A. 1 B. 2 C. 3 D. 4
4 (2024湖州期末)如图所示的频率直方图呈现右拖尾形态,则根据此图作出判断,下列结论中正确的是( )
A. 众数<中位数<平均数
B. 众数<平均数<中位数
C. 中位数<平均数<众数
D. 中位数<众数<平均数
5 (2024福州期末)下图为某地2014年至2023年的粮食年产量折线图,则下列说法中错误的是( )
A. 这10年粮食年产量的极差为16
B. 这10年粮食年产量的70百分位数为35
C. 这10年粮食年产量的平均数为33.7
D. 前5年粮食年产量的方差小于后5年粮食年产量的方差
6 (2023泉州期末)已知一组样本数据共有8个数,其平均数为8,方差为12,将这组样本数据增加两个未知的数据构成一组新的样本数据,已知新的样本数据的平均数为9,则新的样本数据的方差的最小值为( )
A. 10 B. 10.6 C. 12.6 D. 13.6
二、 多项选择题
7 (2024绍兴期末)四位同学各掷大小一致、质地均匀的骰子5次,分别记录每次骰子出现的点数.四位同学的统计结果如下,则可能出现点数6的是( )
A. 平均数为3,中位数为2 B. 平均数为2,方差为2.4
C. 中位数为3,众数为2 D. 中位数为3,方差为2.8
8 (2024杭州期末)本学期某校举行了有关垃圾分类知识的竞赛,随机抽取了100名学生进行成绩统计,发现抽取的学生的成绩都在50~100分之间,进行适当分组后(每组为左闭右开的区间),画出频率直方图如图,则下列说法中正确的是( )
A. 图中x的值为0.030
B. 被抽取的学生中成绩在区间[70,80)的人数为15
C. 估计样本数据的众数为90
D. 估计样本数据的平均数大于中位数
三、 填空题
9 某学校高中三个年级共有团干部56名,现采用分层抽样的方法从中抽取7人进行睡眠时间调查,其中从高一年级抽取了3人,则高一年级团干部的人数为________.
10 (2024温州期末)已知样本数据x1,x2,…,x9的平均数为9,方差为12,现这组样本数据增加一个数据x10,此时新样本数据的平均数为10,则新样本数据的方差为________.
11 2022年第24届冬奥会在北京、延庆和张家口成功举办,出色的赛事组织工作赢得了国际社会的一致称赞.经济效益方面,多项收入也创下历届冬奥会新高.某机构对本届冬奥会各项主要收入进行了统计,得到的数据如图所示.已知赛事转播的收入比政府补贴和特许商品销售的收入之和多27亿元,则估计2022年冬奥会这几项收入总和约为________亿元.(结果保留整数)
四、 解答题
12 (2024河北期末)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率直方图.
(1) 求频率直方图中a的值;
(2) 已知该市有30万居民,估计全市居民中月均用水量不低于3 t的人数,并说明理由;
(3) 估计居民月均用水量的众数、中位数.
13 (2023信阳期末)信阳市旅游部门为了促进信阳生态特色城镇和新农村建设,将甲、乙、丙三家民宿的相关资料放到某网络平台上进行推广宣传. 该平台邀请部分曾在这三家民宿体验过的游客参与调查,得到了这三家民宿的“综合满意度”评分,评分越高表明游客体验越好,现从这三家民宿“综合满意度”的评分中各随机抽取10个评分数据,并对所得数据进行整理、描述和分析,下面给出了部分信息.
①甲、乙两家民宿“综合满意度”评分的折线图:
②丙家民宿“综合满意度”评分:
2.6,4.7,4.5,5.0,4.5,4.8,4.5,3.8,4.5,3.1
③甲、乙、丙三家民宿“综合满意度”评分的平均数、中位数:
甲 乙 丙
平均数 m 4.5 4.2
中位数 4.5 4.7 n
根据以上信息,回答下列问题:
(1) 表中m的值是________,n的值是________;
(2) 设甲、乙、丙三家民宿“综合满意度”评分的方差分别为s,s,s,试比较其大小;
(3) 根据“综合满意度”的评分情况,该平台打算将甲、乙、丙三家民宿中的一家置顶推荐,你认为该平台会将这三家民宿中的哪家置顶推荐?请说明理由(至少从两个方面说明).
第14章 统 计
本 章 复 习
1. B 依次从数表中读出的有效编号为12,02,01,04,15,20,得到选出来的第6个个体的编号为20.
2. C 40%×10=4,又该组数据的40百分位数为22,则=22,解得a=21.
3. C 由频率直方图可知酒精浓度在80 mg/100 mL(含80)以上的频率为(0.01+0.005)×10=0.15,所以样本中属于醉酒驾车的人数约为20×0.15=3.
4. A 由频率直方图可知数据组的众数为左起第2个小矩形下底边中点值,显然在过该中点垂直于横轴的直线及左侧的矩形面积和小于0.5,则众数<中位数.由频率直方图呈现右拖尾形态,得中位数<平均数,所以众数<中位数<平均数.
5. B 对于A,将样本数据从小到大排列为26,28,30,32,32,35,35,38,39,42,这10年的粮食年产量的极差为42-26=16,故A正确;对于B,10×70%=7,结合A选项可知70百分位数为第7个数和第8个数的平均数,即=36.5,故B不正确;对于C,这10年粮食年产量的平均数为×(32+32+30+28+35+38+42+39+26+35)=33.7,故C正确;对于D,结合折线图可知前5年的粮食年产量的波动小于后5年的粮食年产量波动,所以前5年的粮食年产量的方差小于后5年的粮食年产量的方差,故D正确.
6. D 设增加的数为x,y,原来的8个数分别为a1,a2,…,a8,则a1+a2+…+a8=64,a1+a2+…+a8+x+y=90,所以x+y=26.又(ai-8)2=12,即(ai-8)2=96,所以新的样本数据的方差为[(ai-9)2+(x-9)2+(y-9)2]=[(ai-8)2-2(ai-8)+8+(x-9)2+(y-9)2]=(x2+y2-202).因为≥=13,所以x2+y2-202≥136,所以方差的最小值为13.6,当且仅当x=y=13时取到最小值.
7. ACD 对于A,当掷骰子出现的结果为1,1,2,5,6时,满足平均数为3,中位数为2,可以出现点6,故A正确;对于B,若平均数为2,且出现点数6,则方差s2>(6-2)2=3.2>2.4,所以当平均数为2,方差为2.4时,一定不会出现点数6,故B错误;对于C,当掷骰子出现的结果为2,2,3,4,6时,满足中位数为3,众数为2,可以出现点6,故C正确;对于D,当掷骰子出现的结果为1,2,3,3,6时,满足中位数为3,则平均数为=(1+2+3+3+6)=3,方差为s2=[(1-3)2+(2-3)2+(3-3)2+(3-3)2+(6-3)2]=2.8,所以可以出现点6,故D正确.故选ACD.
8. AB 对于A,结合频率直方图的性质可得(0.005+0.01+0.015+x+0.04)×10=1,解得x=0.03,故A正确;对于B,成绩在区间[70,80)的频率为0.015×10=0.15,人数为100×0.15=15,故B正确;对于C,众数为=95,故C错误;对于D,平均成绩为55×0.05+65×0.1+75×0.15+85×0.3+95×0.4=84,低于80分的频率为0.05+0.1+0.15=0.3,设样本数据的中位数为n,则(n-80)×0.030=0.2,解得n≈86.7,平均数小于中位数,故D错误.故选AB.
9. 24 高一年级团干部的人数为56×=24.
10. 19.8 设增加的数为k,则x1+x2+…+x9=81,x1+x2+…+x9+k=100,所以k=19,又因为(xi-9)2=12,即(xi-9)2=108,所以[ (xi-10)2+(k-10)2]=[ (xi-9)2-2(xi-9)+9+81]=19.8.
11. 218 设收入总和为x,则35.4%x-(12.2%+10.8%)x=27,解得x≈218.
12. (1) 由频率直方图知(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,解得a=0.30,
所以频率直方图中a的值为0.30.
(2) 由图得月均用水量不低于3 t的频率为0.5×(0.12+0.08+0.04)=0.12,
所以估计全市居民中月均用水量不低于3 t的人数为300 000×0.12=36 000.
(3) 由图可知众数是=2.25(t).
因为(0.08+0.16+0.30+0.42)×0.5=0.48<0.5,(0.08+0.16+0.30+0.42+0.50)×0.5=0.73>0.5,
所以中位数在区间[2,2.5)上,设中位数为x,
则0.48+0.50(x-2)=0.5,解得x=2.04,
即中位数为2.04 t.
13. (1) 4.5 4.5 甲家民宿“综合满意度”评分为3.2,4.2,5.0,4.5,5.0,4.8,4.5,4.3,5.0,4.5,所以m=×(3.2+4.2+5.0+4.5+5.0+4.8+4.5+4.3+5.0+4.5)=4.5.因为丙家民宿“综合满意度”评分为2.6,4.7,4.5,5.0,4.5,4.8,4.5,3.8,4.5,3.1,从小到大排列为2.6,3.1,3.8,4.5,4.5,4.5,4.5,4.7,4.8,5.0,所以中位数n==4.5.
(2) 根据折线统计图可知乙的评分数据在4分与5分之间波动,甲的数据在3.2分和5分之间波动,丙的数据在2.6分至5分之间波动,所以s
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
