【期末专项培优】角平分线(含解析)2024-2025学年北师大版数学八年级下册
文档属性
| 名称 | 【期末专项培优】角平分线(含解析)2024-2025学年北师大版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览


文档简介
期末专项培优:角平分线
一.选择题(共5小题)
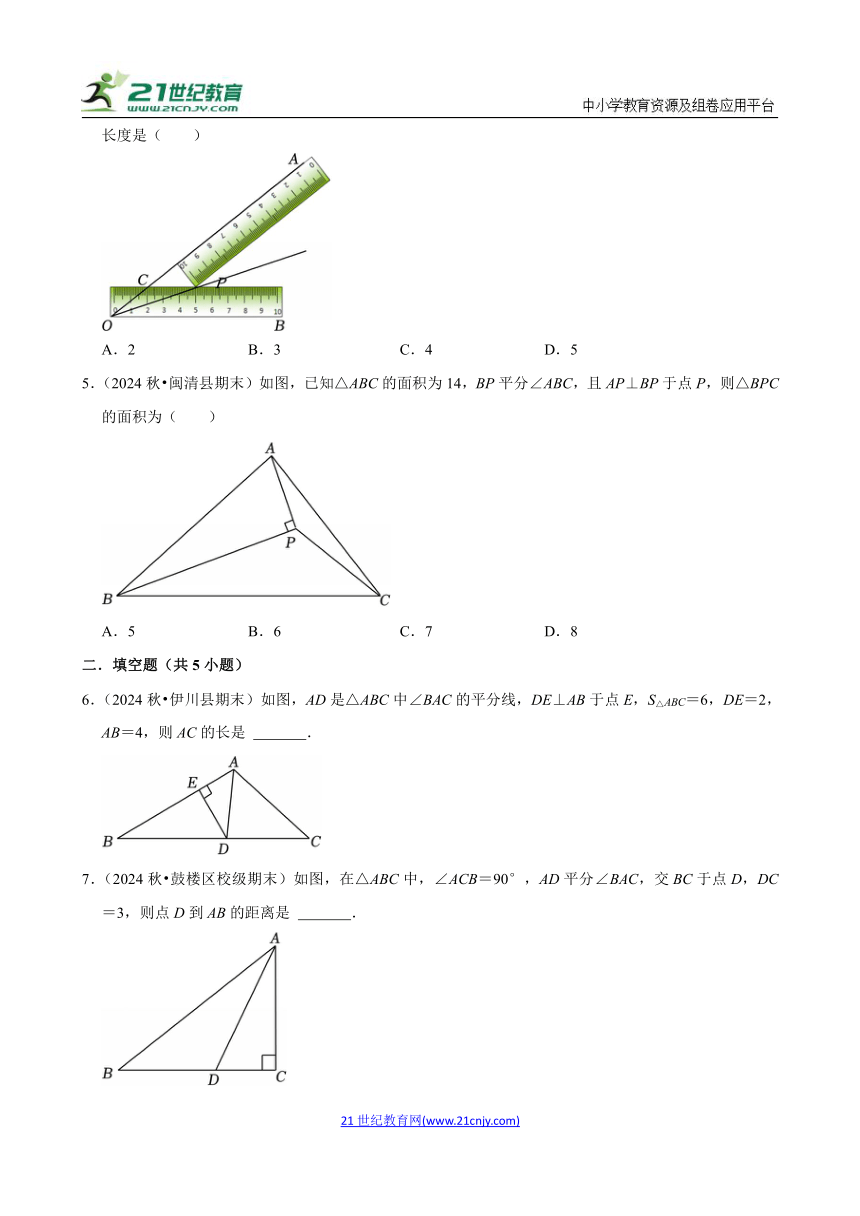
1.(2024秋 新兴县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D.若AC=5cm,则AE+DE=( )
A.2cm B.3cm C.4cm D.5cm
2.(2024秋 合川区期末)如图,在△ABC中,∠C=90°,AD是角平分线,若AB=7,CD=2,则△ABD的面积为( )
A.7 B.8 C.12 D.14
3.(2024秋 湘桥区期末)如图1,这是一个平板电脑支架,由托板、支撑板和底座构成,平板电脑放置在托板上,图2是其侧面结构示意图.现量得托板长AB=10cm,支撑板顶端的C恰好是托板AB的中点,托板AB可绕点C转动,支撑板CD可绕点D转动.当CD⊥AB,且射线DB恰好是∠CDE的平分线时,此时点B到直线DE的距离是( )
A.3cm B.5cm C.6cm D.10cm
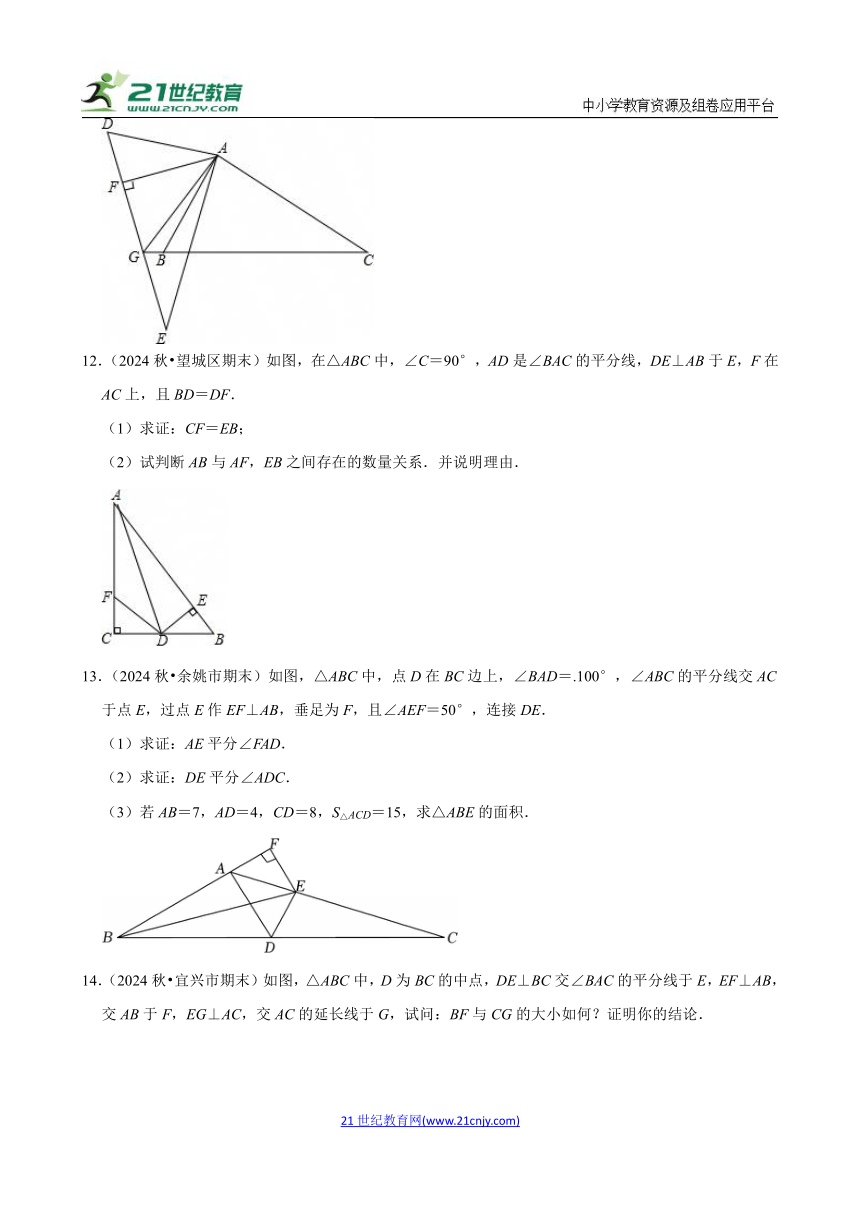
4.(2024秋 东莞市期末)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与另外一把直尺边缘的交点为C,点C,P在这把直尺上的刻度读数分别是2,5,则OC的长度是( )
A.2 B.3 C.4 D.5
5.(2024秋 闽清县期末)如图,已知△ABC的面积为14,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积为( )
A.5 B.6 C.7 D.8
二.填空题(共5小题)
6.(2024秋 伊川县期末)如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=6,DE=2,AB=4,则AC的长是 .
7.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 .
8.(2024秋 宝应县期末)如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是28cm2,DE=4cm,BC=8cm,则AB= cm.
9.(2024秋 裕华区校级期末)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,动点P从点C出发,以每秒2cm的速度按C→A的路径运动,设运动时间为t秒.出发2秒时,△ABP的面积为 cm2;当t= 时,BP恰好平分∠ABC.
10.(2024秋 昌平区期末)如图,点C在∠AOB的平分线上,CD⊥OB于点D,且CD=2,如果E是射线OA上一点,且OE=4,那么△OEC的面积是 .
三.解答题(共5小题)
11.(2024秋 垫江县期末)如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF,求FG的长.
12.(2024秋 望城区期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
13.(2024秋 余姚市期末)如图,△ABC中,点D在BC边上,∠BAD=.100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求证:AE平分∠FAD.
(2)求证:DE平分∠ADC.
(3)若AB=7,AD=4,CD=8,S△ACD=15,求△ABE的面积.
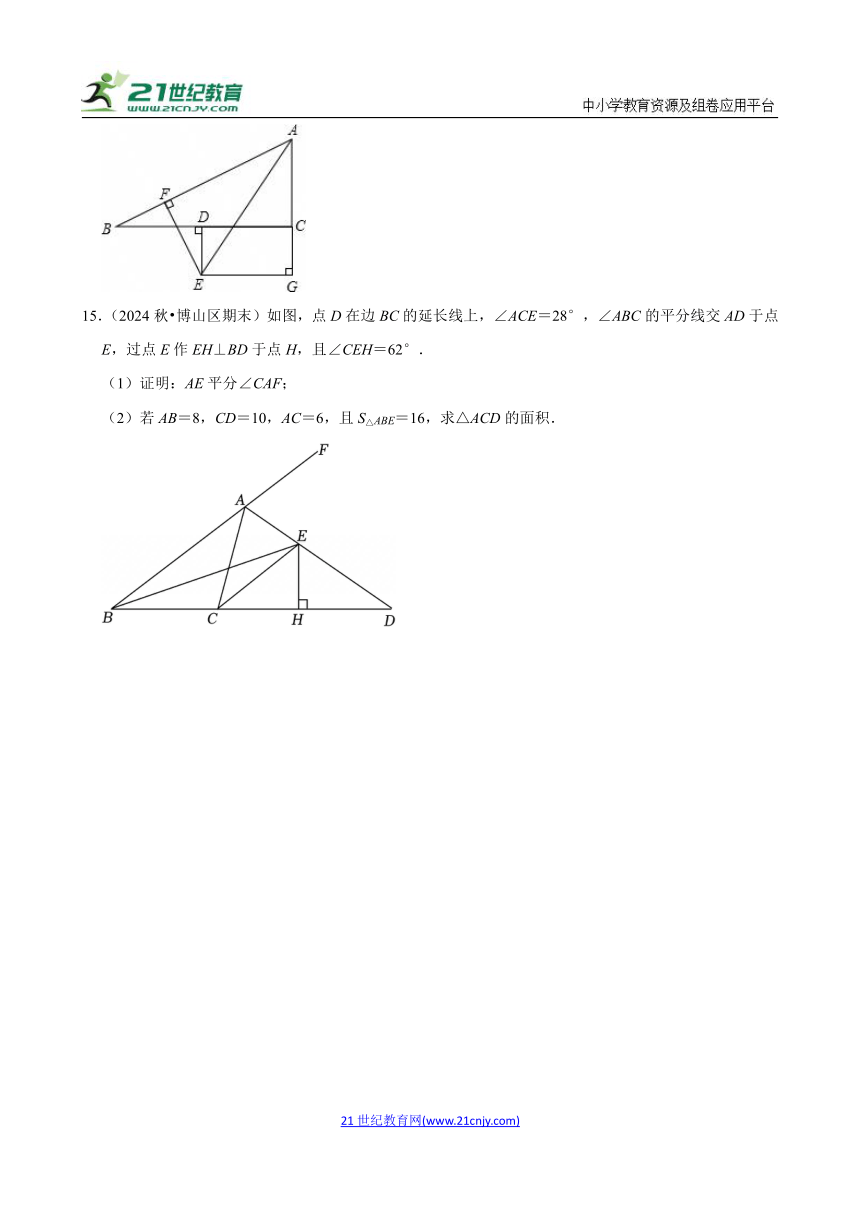
14.(2024秋 宜兴市期末)如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于E,EF⊥AB,交AB于F,EG⊥AC,交AC的延长线于G,试问:BF与CG的大小如何?证明你的结论.
15.(2024秋 博山区期末)如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
期末专项培优:角平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 新兴县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D.若AC=5cm,则AE+DE=( )
A.2cm B.3cm C.4cm D.5cm
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】D
【分析】根据角平分线的性质得到ED=EC,则AE+ED=AC.
【解答】解:∵BE平分∠ABC,DE⊥AB,EC⊥BC,
∴ED=EC,
∴AE+ED=AE+EC=AC=5cm.
故选:D.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
2.(2024秋 合川区期末)如图,在△ABC中,∠C=90°,AD是角平分线,若AB=7,CD=2,则△ABD的面积为( )
A.7 B.8 C.12 D.14
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据角平分线上的点到角两边的距离相等,即可得到△ABD的面积.
【解答】解:过点D作DE⊥AB于点E,
∵∠C=90°,AD是角平分线,
∴DE=CD=7,
∴△ABD的面积,
故选:A.
【点评】本题考查角平分线的性质,掌握角平分线的性质是解题的关键.
3.(2024秋 湘桥区期末)如图1,这是一个平板电脑支架,由托板、支撑板和底座构成,平板电脑放置在托板上,图2是其侧面结构示意图.现量得托板长AB=10cm,支撑板顶端的C恰好是托板AB的中点,托板AB可绕点C转动,支撑板CD可绕点D转动.当CD⊥AB,且射线DB恰好是∠CDE的平分线时,此时点B到直线DE的距离是( )
A.3cm B.5cm C.6cm D.10cm
【考点】角平分线的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】B
【分析】根据C是AB的中点可求BC的长度,再根据角平分线上的点到角两边距离相等即可求解.
【解答】解:过点B作BF⊥DE,垂足为点F,
∵C是AB的中点,AB=10cm,
∴,
∵CD⊥AB,BF⊥DE,射线DB是∠CDE的平分线,
∴BC=BF=5cm,
故选:B.
【点评】本题主要考查了角平分线的性质,解题的关键是熟练掌握角平分线上的点到角两边的距离相等.
4.(2024秋 东莞市期末)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与另外一把直尺边缘的交点为C,点C,P在这把直尺上的刻度读数分别是2,5,则OC的长度是( )
A.2 B.3 C.4 D.5
【考点】角平分线的性质;平行线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】B
【分析】过P作PN⊥OB于N,由角平分线性质定理的逆定理推出PO平分∠AOB,得到∠COP=∠NOP,由平行线的性质推出∠CPO=∠NOP,得到∠COP=∠CPO,因此OC=PC,由PC=5﹣2=3(cm),即可得到OC的长度是3cm.
【解答】解:过P作PN⊥OB于N,
由题意得:PM=PN,
∵PM⊥OA,
∴PO平分∠AOB,
∴∠COP=∠NOP,
∵PC∥OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC,
∵C、P在这把直尺上的刻度读数分别是2、5,
∴PC=5﹣2=3(cm),
∴OC的长度是3cm.
故选:B.
【点评】本题考查角角平分线的性质,平行线的性质,解答本题的关键是证明PO平分∠AOB.
5.(2024秋 闽清县期末)如图,已知△ABC的面积为14,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积为( )
A.5 B.6 C.7 D.8
【考点】角平分线的性质;三角形的面积;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】延长AP交BC于D,证明△ABP≌△DBP(ASA)得到AP=DP,再根据三角形中线平分三角形面积即可得到答案.
【解答】解:如图所示,延长AP交BC于D,
由角平分线定义可知:∠ABP=∠DBP,
∴∠APB=∠DPB=90°,
∴△ABP≌△DBP(ASA),
∴AP=DP,
∴,
∴.
故选:C.
【点评】本题主要考查了全等三角形的性质与判定,角平分线的定义,三角形中线平分三角形面积等知识,解题的关键是正确寻找全等三角形解决问题.
二.填空题(共5小题)
6.(2024秋 伊川县期末)如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=6,DE=2,AB=4,则AC的长是 2 .
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】2.
【分析】首先根据角平分线上的点到角两边的距离相等可得DE=DF=2,根据S△ADC=S△ABC﹣S△ABD=2可以求出△ADC的面积为2,再根据三角形的面积公式可得,可以求出AC=2.
【解答】解:如图所示,过点D作DF⊥AC于点F,
∵AD是∠ABC的平分线,DE⊥AB于点E,DE=2,
∴DE=DF=2,
∵S△ABC=6,AB=4,
∴,
∴S△ADC=S△ABC﹣S△ABD=6﹣4=2,
又∵,
∴AC=2.
故答案为:2.
【点评】本题考查了三角形的面积公式、角平分线的性质,熟知角平分线上的点到角的两边距离相等是解题的关键.
7.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 3 .
【考点】角平分线的性质;点到直线的距离.
【专题】线段、角、相交线与平行线;运算能力.
【答案】3.
【分析】根据角平分线的性质即可得到答案.
【解答】解:过D作DE⊥AB交AB于点E,
∵∠ACB=90°,AD平分∠BAC,
∴DE=DC,
∵DC=3,
∴DE=DC=3,
∴D到AB的距离是3.
故答案为:3.
【点评】本题主要考查角平分线的性质,掌握角平分线的性质是解题的关键.
8.(2024秋 宝应县期末)如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是28cm2,DE=4cm,BC=8cm,则AB= 6 cm.
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】6.
【分析】由角平分线的性质推出DF=DE=4cm,由三角形面积公式得到AB DEBC DF=28cm2,即可求出AB的长.
【解答】解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB于E,
∴DF=DE=4cm,
∵△ABC的面积=△ABD的面积+△CBD的面积,
∴AB DEBC DF=28cm2,
∴AB×48×4=28,
∴AB=6cm.
故答案为:6.
【点评】本题考查角平分线的性质,三角形的面积,关键是由角平分线的性质推出DF=DE.
9.(2024秋 裕华区校级期末)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,动点P从点C出发,以每秒2cm的速度按C→A的路径运动,设运动时间为t秒.出发2秒时,△ABP的面积为 12 cm2;当t= 1.5 时,BP恰好平分∠ABC.
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】12,1.5.
【分析】根据勾股定理求出AC,根据三角形的面积公式计算即可,根据角平分线的性得到PH=PC,再由S△ABC=S△PBC+S△ABP即可得出结论.
【解答】解:∵∠C=90°,AB=10cm,BC=6cm,
∴AC8(cm),
当t=2时,AP=8﹣2×2=4(cm),
∴△ABP的面积=×4×6=12(cm2),
当BP平分∠ABC时,作PH⊥AB于H,
则PH=PC=2t,
∵S△ABC=S△PBC+S△ABP,
∴AC BC=BC PC+AB PH,即8×6=12t+20t,
解得,t=1.5,
则t=1.5s时,BP恰好平分∠ABC.
故答案为:12,1.5.
【点评】本题考查的是勾股定理,熟知直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.
10.(2024秋 昌平区期末)如图,点C在∠AOB的平分线上,CD⊥OB于点D,且CD=2,如果E是射线OA上一点,且OE=4,那么△OEC的面积是 4 .
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】4.
【分析】过点C作CG⊥OA于G,根据角平分线的性质得到CG=CD=2,再根据三角形面积公式计算即可.
【解答】解:如图,过点C作CG⊥OA于G,
∵点C在∠AOB的平分线上,CD⊥OB,CG⊥OA,CD=2,
∴CG=CD=2,
∴S△OECOE CG4×2=4,
故答案为:4.
【点评】本题考查的是角平分线的性质,熟记角的平分线上的点到角的两边的距离相等是解题的关键.
三.解答题(共5小题)
11.(2024秋 垫江县期末)如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF,求FG的长.
【考点】角平分线的性质;三角形的面积;全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】(1)先过点A作AH⊥BC于H,判定△ABC≌△AED,得出AF=AH,再判定Rt△AFG≌Rt△AHG,即可得出∠AGF=∠AGH;
(2)先判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,再根据Rt△AFG≌Rt△AHG,求得Rt△AFG的面积=3,进而得到FG的长.
【解答】解:(1)过点A作AH⊥BC于H,
∵△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,
∴△ABC≌△ADE(SAS),
∴S△ABC=S△AED,
又∵AF⊥DE,
即DE×AFBC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,AG=AG,
∴Rt△AFG≌Rt△AHG(HL),
∴∠AGF=∠AGH,
即GA平分∠DGB;
(注:由AF=AH,AF⊥DE,AH⊥BC,也可以直接得到GA平分∠DGB.)
(2)∵△ABC≌△ADE,
∴AD=AB,
又∵AF⊥DE,AH⊥BC,AF=AH,
∴Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF,
∴FG3,
解得FG=4.
【点评】本题主要考查了全等三角形的判定与性质,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.
12.(2024秋 望城区期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
【考点】角平分线的性质.
【答案】见试题解答内容
【分析】(1)根据角平分线的性质得到DC=DE,证明Rt△FCD≌Rt△BED,根据全等三角形的性质证明;
(2)证明Rt△ACD≌Rt△AED,根据全等三角形的性质证明.
【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB;
(2)解:AB=AF+2BE,
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
13.(2024秋 余姚市期末)如图,△ABC中,点D在BC边上,∠BAD=.100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求证:AE平分∠FAD.
(2)求证:DE平分∠ADC.
(3)若AB=7,AD=4,CD=8,S△ACD=15,求△ABE的面积.
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)证明见解析;
(2)证明见解析;
(3).
【分析】(1)由直角三角形的性质求出∠EAF=40°,由平角定义即可求出∠DAE的度数,再根据角平分线定义即可得证;
(2)过E作EM⊥AD于M,EN⊥BC于N,由角平分线的性质推出EF=EN,FE=EM,得到EM=EN,于是推出DE平分∠ADC;
(3)由△ACD的面积=△ADE的面积+△CDE的面积,得到AD EM+CD EN=18,即可求出EM=3,得到EF=3,由三角形面积公式即可求出△ABE的面积.
【解答】(1)证明:∵EF⊥AB,
∴∠AFE=90°,
∵∠AEF=50°,
∴∠EAF=90°﹣∠AEF=90°﹣50°=40°,
∵∠BAD=100°,
∴∠DAE=180°﹣100°﹣40°=40°=∠EAF,
∴AE平分∠FAD;
(2)证明:过E作EM⊥AD于M,EN⊥BC于N,
∵BE平分∠ABC,EF⊥AB,
∴EF=EN,
∵AE平分∠DAF,EF⊥AB,
∴FE=EM,
∴EM=EN,
∵EM⊥AD,EN⊥CD,
∴DE平分∠ADC;
(3)解:∵△ACD的面积=△ADE的面积+△CDE的面积,
∴AD EMCD EN=15,
∴(AD+CD) EM=15,
∴(4+8)×EM=15,
∴EM,
∴EF,
∴△ABE的面积AB EF7.
【点评】本题考查角平分线的性质,关键是掌握角平分线的性质定理及其逆定理.
14.(2024秋 宜兴市期末)如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于E,EF⊥AB,交AB于F,EG⊥AC,交AC的延长线于G,试问:BF与CG的大小如何?证明你的结论.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】探究型.
【答案】见试题解答内容
【分析】连EB、EC,根据角平分线性质得EF=EG;根据垂直平分线的性质得EB=EC;再根据“HL”定理证明Rt△EFB≌Rt△EGC,从而得BF=CG.
【解答】解:相等.
证明如下:连EB、EC,
∵AE是∠BAC的平分线,
且EF⊥AB于F,EG⊥AC于G,
∴EF=EG.
∵ED⊥BC于D,D是BC的中点,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
,
∴Rt△EFB≌Rt△EGC(HL),
∴BF=CG.
【点评】本题考查了角平分线性质和垂直平分线的性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键.
15.(2024秋 博山区期末)如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;运算能力.
【答案】见试题解答内容
【分析】(1)如图,过E点分别作EM⊥BF于M,EN⊥AC与N,根据角平分线的性质定理以及角平分线的定义可得EM=EH、CE平分∠ACD、EN=EH,最后根据角平分线的判定定理即可解答;
(2)根据S△ACD=S△ACE+S△CED结合已知条件可得EM=4,最后运用三角形的面积公式即可解答.
【解答】(1)证明:过E点作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=28°,∠CEH=62°,
∴∠HCE=90°﹣∠CEH=90°﹣62°=28°=∠ACE,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(2)∵AB=8,CD=10,AC=6,且S△ABE=16,
∴,
∴EM=4,
∴EN=EH=EM=4,
∴S△ACD=S△ACE+S△CED
=32,
∴△ACD的面积为32.
【点评】本题考查角平分线的性质与判定、直角三角形两锐角互余、三角形的面积,掌握角平分线的性质与判定定理是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 新兴县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D.若AC=5cm,则AE+DE=( )
A.2cm B.3cm C.4cm D.5cm
2.(2024秋 合川区期末)如图,在△ABC中,∠C=90°,AD是角平分线,若AB=7,CD=2,则△ABD的面积为( )
A.7 B.8 C.12 D.14
3.(2024秋 湘桥区期末)如图1,这是一个平板电脑支架,由托板、支撑板和底座构成,平板电脑放置在托板上,图2是其侧面结构示意图.现量得托板长AB=10cm,支撑板顶端的C恰好是托板AB的中点,托板AB可绕点C转动,支撑板CD可绕点D转动.当CD⊥AB,且射线DB恰好是∠CDE的平分线时,此时点B到直线DE的距离是( )
A.3cm B.5cm C.6cm D.10cm
4.(2024秋 东莞市期末)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与另外一把直尺边缘的交点为C,点C,P在这把直尺上的刻度读数分别是2,5,则OC的长度是( )
A.2 B.3 C.4 D.5
5.(2024秋 闽清县期末)如图,已知△ABC的面积为14,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积为( )
A.5 B.6 C.7 D.8
二.填空题(共5小题)
6.(2024秋 伊川县期末)如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=6,DE=2,AB=4,则AC的长是 .
7.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 .
8.(2024秋 宝应县期末)如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是28cm2,DE=4cm,BC=8cm,则AB= cm.
9.(2024秋 裕华区校级期末)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,动点P从点C出发,以每秒2cm的速度按C→A的路径运动,设运动时间为t秒.出发2秒时,△ABP的面积为 cm2;当t= 时,BP恰好平分∠ABC.
10.(2024秋 昌平区期末)如图,点C在∠AOB的平分线上,CD⊥OB于点D,且CD=2,如果E是射线OA上一点,且OE=4,那么△OEC的面积是 .
三.解答题(共5小题)
11.(2024秋 垫江县期末)如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF,求FG的长.
12.(2024秋 望城区期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
13.(2024秋 余姚市期末)如图,△ABC中,点D在BC边上,∠BAD=.100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求证:AE平分∠FAD.
(2)求证:DE平分∠ADC.
(3)若AB=7,AD=4,CD=8,S△ACD=15,求△ABE的面积.
14.(2024秋 宜兴市期末)如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于E,EF⊥AB,交AB于F,EG⊥AC,交AC的延长线于G,试问:BF与CG的大小如何?证明你的结论.
15.(2024秋 博山区期末)如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
期末专项培优:角平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 新兴县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D.若AC=5cm,则AE+DE=( )
A.2cm B.3cm C.4cm D.5cm
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】D
【分析】根据角平分线的性质得到ED=EC,则AE+ED=AC.
【解答】解:∵BE平分∠ABC,DE⊥AB,EC⊥BC,
∴ED=EC,
∴AE+ED=AE+EC=AC=5cm.
故选:D.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
2.(2024秋 合川区期末)如图,在△ABC中,∠C=90°,AD是角平分线,若AB=7,CD=2,则△ABD的面积为( )
A.7 B.8 C.12 D.14
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据角平分线上的点到角两边的距离相等,即可得到△ABD的面积.
【解答】解:过点D作DE⊥AB于点E,
∵∠C=90°,AD是角平分线,
∴DE=CD=7,
∴△ABD的面积,
故选:A.
【点评】本题考查角平分线的性质,掌握角平分线的性质是解题的关键.
3.(2024秋 湘桥区期末)如图1,这是一个平板电脑支架,由托板、支撑板和底座构成,平板电脑放置在托板上,图2是其侧面结构示意图.现量得托板长AB=10cm,支撑板顶端的C恰好是托板AB的中点,托板AB可绕点C转动,支撑板CD可绕点D转动.当CD⊥AB,且射线DB恰好是∠CDE的平分线时,此时点B到直线DE的距离是( )
A.3cm B.5cm C.6cm D.10cm
【考点】角平分线的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】B
【分析】根据C是AB的中点可求BC的长度,再根据角平分线上的点到角两边距离相等即可求解.
【解答】解:过点B作BF⊥DE,垂足为点F,
∵C是AB的中点,AB=10cm,
∴,
∵CD⊥AB,BF⊥DE,射线DB是∠CDE的平分线,
∴BC=BF=5cm,
故选:B.
【点评】本题主要考查了角平分线的性质,解题的关键是熟练掌握角平分线上的点到角两边的距离相等.
4.(2024秋 东莞市期末)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与另外一把直尺边缘的交点为C,点C,P在这把直尺上的刻度读数分别是2,5,则OC的长度是( )
A.2 B.3 C.4 D.5
【考点】角平分线的性质;平行线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】B
【分析】过P作PN⊥OB于N,由角平分线性质定理的逆定理推出PO平分∠AOB,得到∠COP=∠NOP,由平行线的性质推出∠CPO=∠NOP,得到∠COP=∠CPO,因此OC=PC,由PC=5﹣2=3(cm),即可得到OC的长度是3cm.
【解答】解:过P作PN⊥OB于N,
由题意得:PM=PN,
∵PM⊥OA,
∴PO平分∠AOB,
∴∠COP=∠NOP,
∵PC∥OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC,
∵C、P在这把直尺上的刻度读数分别是2、5,
∴PC=5﹣2=3(cm),
∴OC的长度是3cm.
故选:B.
【点评】本题考查角角平分线的性质,平行线的性质,解答本题的关键是证明PO平分∠AOB.
5.(2024秋 闽清县期末)如图,已知△ABC的面积为14,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积为( )
A.5 B.6 C.7 D.8
【考点】角平分线的性质;三角形的面积;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】延长AP交BC于D,证明△ABP≌△DBP(ASA)得到AP=DP,再根据三角形中线平分三角形面积即可得到答案.
【解答】解:如图所示,延长AP交BC于D,
由角平分线定义可知:∠ABP=∠DBP,
∴∠APB=∠DPB=90°,
∴△ABP≌△DBP(ASA),
∴AP=DP,
∴,
∴.
故选:C.
【点评】本题主要考查了全等三角形的性质与判定,角平分线的定义,三角形中线平分三角形面积等知识,解题的关键是正确寻找全等三角形解决问题.
二.填空题(共5小题)
6.(2024秋 伊川县期末)如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=6,DE=2,AB=4,则AC的长是 2 .
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】2.
【分析】首先根据角平分线上的点到角两边的距离相等可得DE=DF=2,根据S△ADC=S△ABC﹣S△ABD=2可以求出△ADC的面积为2,再根据三角形的面积公式可得,可以求出AC=2.
【解答】解:如图所示,过点D作DF⊥AC于点F,
∵AD是∠ABC的平分线,DE⊥AB于点E,DE=2,
∴DE=DF=2,
∵S△ABC=6,AB=4,
∴,
∴S△ADC=S△ABC﹣S△ABD=6﹣4=2,
又∵,
∴AC=2.
故答案为:2.
【点评】本题考查了三角形的面积公式、角平分线的性质,熟知角平分线上的点到角的两边距离相等是解题的关键.
7.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 3 .
【考点】角平分线的性质;点到直线的距离.
【专题】线段、角、相交线与平行线;运算能力.
【答案】3.
【分析】根据角平分线的性质即可得到答案.
【解答】解:过D作DE⊥AB交AB于点E,
∵∠ACB=90°,AD平分∠BAC,
∴DE=DC,
∵DC=3,
∴DE=DC=3,
∴D到AB的距离是3.
故答案为:3.
【点评】本题主要考查角平分线的性质,掌握角平分线的性质是解题的关键.
8.(2024秋 宝应县期末)如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是28cm2,DE=4cm,BC=8cm,则AB= 6 cm.
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】6.
【分析】由角平分线的性质推出DF=DE=4cm,由三角形面积公式得到AB DEBC DF=28cm2,即可求出AB的长.
【解答】解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB于E,
∴DF=DE=4cm,
∵△ABC的面积=△ABD的面积+△CBD的面积,
∴AB DEBC DF=28cm2,
∴AB×48×4=28,
∴AB=6cm.
故答案为:6.
【点评】本题考查角平分线的性质,三角形的面积,关键是由角平分线的性质推出DF=DE.
9.(2024秋 裕华区校级期末)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,动点P从点C出发,以每秒2cm的速度按C→A的路径运动,设运动时间为t秒.出发2秒时,△ABP的面积为 12 cm2;当t= 1.5 时,BP恰好平分∠ABC.
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】12,1.5.
【分析】根据勾股定理求出AC,根据三角形的面积公式计算即可,根据角平分线的性得到PH=PC,再由S△ABC=S△PBC+S△ABP即可得出结论.
【解答】解:∵∠C=90°,AB=10cm,BC=6cm,
∴AC8(cm),
当t=2时,AP=8﹣2×2=4(cm),
∴△ABP的面积=×4×6=12(cm2),
当BP平分∠ABC时,作PH⊥AB于H,
则PH=PC=2t,
∵S△ABC=S△PBC+S△ABP,
∴AC BC=BC PC+AB PH,即8×6=12t+20t,
解得,t=1.5,
则t=1.5s时,BP恰好平分∠ABC.
故答案为:12,1.5.
【点评】本题考查的是勾股定理,熟知直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.
10.(2024秋 昌平区期末)如图,点C在∠AOB的平分线上,CD⊥OB于点D,且CD=2,如果E是射线OA上一点,且OE=4,那么△OEC的面积是 4 .
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】4.
【分析】过点C作CG⊥OA于G,根据角平分线的性质得到CG=CD=2,再根据三角形面积公式计算即可.
【解答】解:如图,过点C作CG⊥OA于G,
∵点C在∠AOB的平分线上,CD⊥OB,CG⊥OA,CD=2,
∴CG=CD=2,
∴S△OECOE CG4×2=4,
故答案为:4.
【点评】本题考查的是角平分线的性质,熟记角的平分线上的点到角的两边的距离相等是解题的关键.
三.解答题(共5小题)
11.(2024秋 垫江县期末)如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF,求FG的长.
【考点】角平分线的性质;三角形的面积;全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】(1)先过点A作AH⊥BC于H,判定△ABC≌△AED,得出AF=AH,再判定Rt△AFG≌Rt△AHG,即可得出∠AGF=∠AGH;
(2)先判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,再根据Rt△AFG≌Rt△AHG,求得Rt△AFG的面积=3,进而得到FG的长.
【解答】解:(1)过点A作AH⊥BC于H,
∵△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,
∴△ABC≌△ADE(SAS),
∴S△ABC=S△AED,
又∵AF⊥DE,
即DE×AFBC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,AG=AG,
∴Rt△AFG≌Rt△AHG(HL),
∴∠AGF=∠AGH,
即GA平分∠DGB;
(注:由AF=AH,AF⊥DE,AH⊥BC,也可以直接得到GA平分∠DGB.)
(2)∵△ABC≌△ADE,
∴AD=AB,
又∵AF⊥DE,AH⊥BC,AF=AH,
∴Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF,
∴FG3,
解得FG=4.
【点评】本题主要考查了全等三角形的判定与性质,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.
12.(2024秋 望城区期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
【考点】角平分线的性质.
【答案】见试题解答内容
【分析】(1)根据角平分线的性质得到DC=DE,证明Rt△FCD≌Rt△BED,根据全等三角形的性质证明;
(2)证明Rt△ACD≌Rt△AED,根据全等三角形的性质证明.
【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB;
(2)解:AB=AF+2BE,
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
13.(2024秋 余姚市期末)如图,△ABC中,点D在BC边上,∠BAD=.100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求证:AE平分∠FAD.
(2)求证:DE平分∠ADC.
(3)若AB=7,AD=4,CD=8,S△ACD=15,求△ABE的面积.
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)证明见解析;
(2)证明见解析;
(3).
【分析】(1)由直角三角形的性质求出∠EAF=40°,由平角定义即可求出∠DAE的度数,再根据角平分线定义即可得证;
(2)过E作EM⊥AD于M,EN⊥BC于N,由角平分线的性质推出EF=EN,FE=EM,得到EM=EN,于是推出DE平分∠ADC;
(3)由△ACD的面积=△ADE的面积+△CDE的面积,得到AD EM+CD EN=18,即可求出EM=3,得到EF=3,由三角形面积公式即可求出△ABE的面积.
【解答】(1)证明:∵EF⊥AB,
∴∠AFE=90°,
∵∠AEF=50°,
∴∠EAF=90°﹣∠AEF=90°﹣50°=40°,
∵∠BAD=100°,
∴∠DAE=180°﹣100°﹣40°=40°=∠EAF,
∴AE平分∠FAD;
(2)证明:过E作EM⊥AD于M,EN⊥BC于N,
∵BE平分∠ABC,EF⊥AB,
∴EF=EN,
∵AE平分∠DAF,EF⊥AB,
∴FE=EM,
∴EM=EN,
∵EM⊥AD,EN⊥CD,
∴DE平分∠ADC;
(3)解:∵△ACD的面积=△ADE的面积+△CDE的面积,
∴AD EMCD EN=15,
∴(AD+CD) EM=15,
∴(4+8)×EM=15,
∴EM,
∴EF,
∴△ABE的面积AB EF7.
【点评】本题考查角平分线的性质,关键是掌握角平分线的性质定理及其逆定理.
14.(2024秋 宜兴市期末)如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于E,EF⊥AB,交AB于F,EG⊥AC,交AC的延长线于G,试问:BF与CG的大小如何?证明你的结论.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】探究型.
【答案】见试题解答内容
【分析】连EB、EC,根据角平分线性质得EF=EG;根据垂直平分线的性质得EB=EC;再根据“HL”定理证明Rt△EFB≌Rt△EGC,从而得BF=CG.
【解答】解:相等.
证明如下:连EB、EC,
∵AE是∠BAC的平分线,
且EF⊥AB于F,EG⊥AC于G,
∴EF=EG.
∵ED⊥BC于D,D是BC的中点,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
,
∴Rt△EFB≌Rt△EGC(HL),
∴BF=CG.
【点评】本题考查了角平分线性质和垂直平分线的性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键.
15.(2024秋 博山区期末)如图,点D在边BC的延长线上,∠ACE=28°,∠ABC的平分线交AD于点E,过点E作EH⊥BD于点H,且∠CEH=62°.
(1)证明:AE平分∠CAF;
(2)若AB=8,CD=10,AC=6,且S△ABE=16,求△ACD的面积.
【考点】角平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;运算能力.
【答案】见试题解答内容
【分析】(1)如图,过E点分别作EM⊥BF于M,EN⊥AC与N,根据角平分线的性质定理以及角平分线的定义可得EM=EH、CE平分∠ACD、EN=EH,最后根据角平分线的判定定理即可解答;
(2)根据S△ACD=S△ACE+S△CED结合已知条件可得EM=4,最后运用三角形的面积公式即可解答.
【解答】(1)证明:过E点作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=28°,∠CEH=62°,
∴∠HCE=90°﹣∠CEH=90°﹣62°=28°=∠ACE,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF;
(2)∵AB=8,CD=10,AC=6,且S△ABE=16,
∴,
∴EM=4,
∴EN=EH=EM=4,
∴S△ACD=S△ACE+S△CED
=32,
∴△ACD的面积为32.
【点评】本题考查角平分线的性质与判定、直角三角形两锐角互余、三角形的面积,掌握角平分线的性质与判定定理是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
