【中考押题卷】2025年北师大版中考数学考前冲刺:圆周角与圆心角的关系(含解析)
文档属性
| 名称 | 【中考押题卷】2025年北师大版中考数学考前冲刺:圆周角与圆心角的关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:09:46 | ||
图片预览



文档简介
中考押题卷:圆周角与圆心角的关系
一.选择题(共5小题)
1.(2024秋 清江浦区期末)如图,∠APB的边交⊙O于A、B、C、D,、、、的度数分别为α、β、γ、θ,若要确定∠APB的大小,则需要确定的弧的度数是( )
A.α、β B.β、γ C.γ、θ D.α、γ
2.(2024秋 济南期末)如图,四边形ABCD是圆O的内接四边形,∠C=110°,则∠A的度数为( )
A.55° B.60° C.70° D.80°
3.(2024秋 包河区校级期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若∠BOD=40°,则∠BAC的度数为( )
A.20° B.50° C.40° D.25°
4.(2024秋 临潼区期末)如图,BC为⊙O的直径,D为的中点,,连接AB和AD,AD交BC于点E,则∠DEC的度数为( )
A.115° B.110° C.105° D.100°
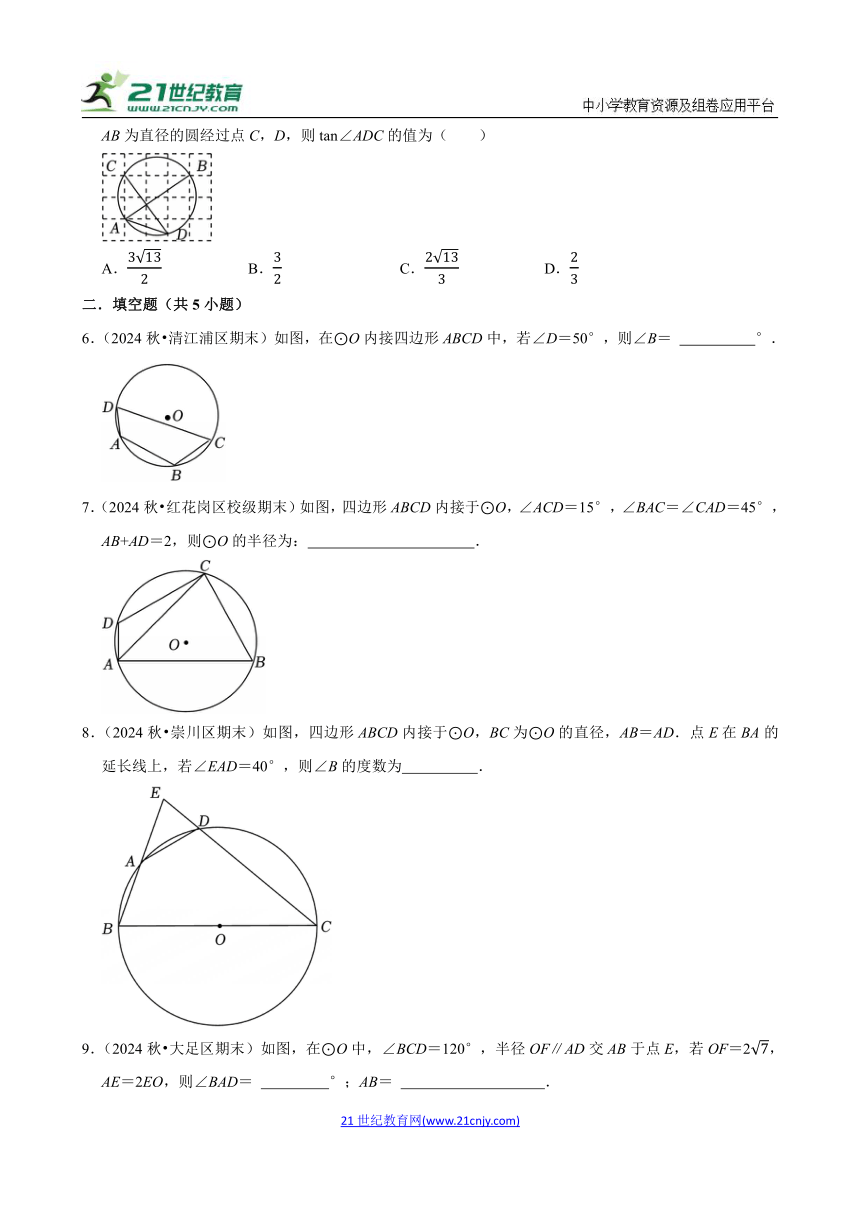
5.(2024秋 长春校级期末)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 清江浦区期末)如图,在⊙O内接四边形ABCD中,若∠D=50°,则∠B= °.
7.(2024秋 红花岗区校级期末)如图,四边形ABCD内接于⊙O,∠ACD=15°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径为: .
8.(2024秋 崇川区期末)如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AB=AD.点E在BA的延长线上,若∠EAD=40°,则∠B的度数为 .
9.(2024秋 大足区期末)如图,在⊙O中,∠BCD=120°,半径OF∥AD交AB于点E,若OF=2,AE=2EO,则∠BAD= °;AB= .
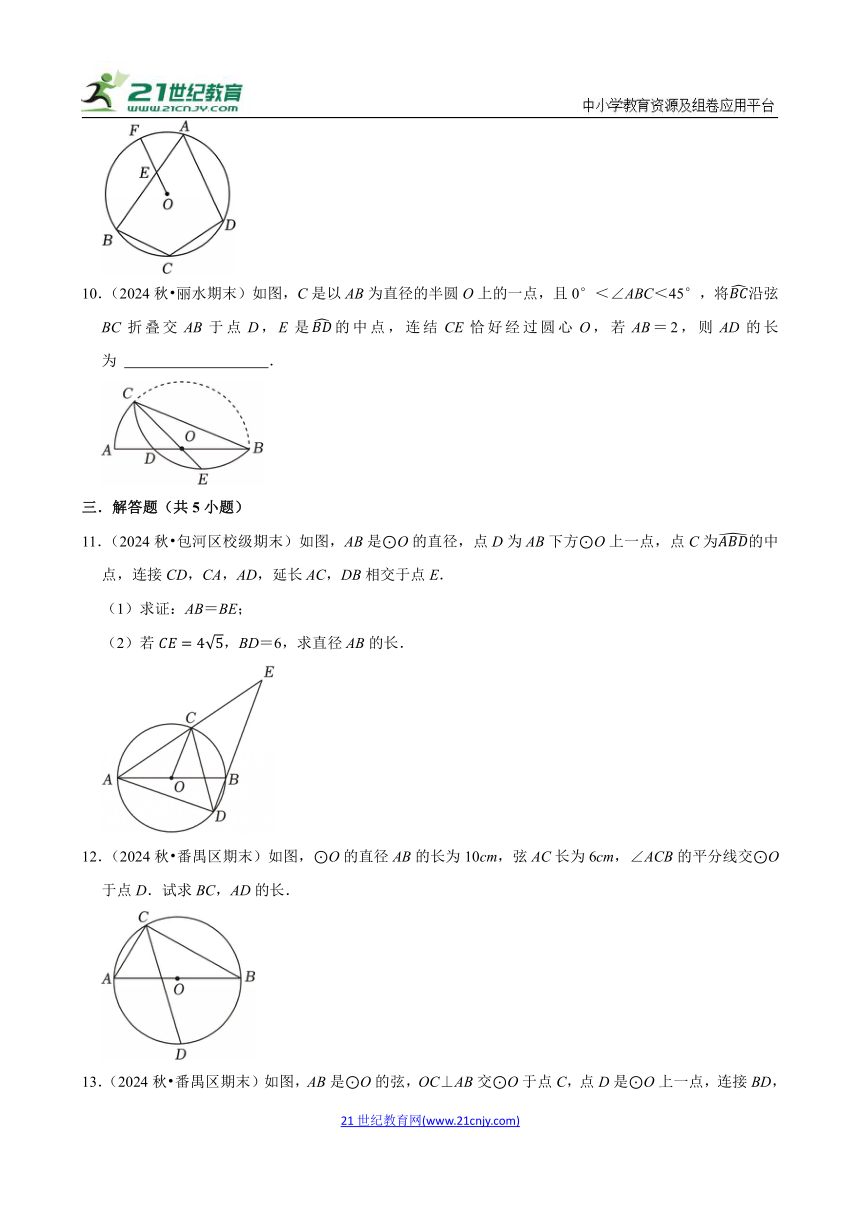
10.(2024秋 丽水期末)如图,C是以AB为直径的半圆O上的一点,且0°<∠ABC<45°,将沿弦BC折叠交AB于点D,E是的中点,连结CE恰好经过圆心O,若AB=2,则AD的长为 .
三.解答题(共5小题)
11.(2024秋 包河区校级期末)如图,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连接CD,CA,AD,延长AC,DB相交于点E.
(1)求证:AB=BE;
(2)若,BD=6,求直径AB的长.
12.(2024秋 番禺区期末)如图,⊙O的直径AB的长为10cm,弦AC长为6cm,∠ACB的平分线交⊙O于点D.试求BC,AD的长.
13.(2024秋 番禺区期末)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,求∠OAB的度数.
14.(2024秋 建邺区期末)如图,在⊙O中,弦AC,BD相交于点M,且AM=BM.求证:CM=DM.
15.(2024秋 白云区期末)如图,OA、OB、OC都是⊙O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=8,,求⊙O的半径.
中考押题卷:圆周角与圆心角的关系
参考答案与试题解析
题号 1 2 3 4 5
答案 D C A C D
一.选择题(共5小题)
1.(2024秋 清江浦区期末)如图,∠APB的边交⊙O于A、B、C、D,、、、的度数分别为α、β、γ、θ,若要确定∠APB的大小,则需要确定的弧的度数是( )
A.α、β B.β、γ C.γ、θ D.α、γ
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】D
【分析】连接BD,根据已知易得:∠ADBα,∠DBCγ,然后利用三角形的外角性质进行计算即可解答.
【解答】解:连接BD,
∵、的度数分别为α、γ,
∴∠ADBα,∠DBCγ,
∵∠ADB是△DBP的一个外角,
∴∠APB=∠ADB﹣∠DBCαγ,
故选:D.
【点评】本题考查了圆周角定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
2.(2024秋 济南期末)如图,四边形ABCD是圆O的内接四边形,∠C=110°,则∠A的度数为( )
A.55° B.60° C.70° D.80°
【考点】圆内接四边形的性质.
【专题】圆的有关概念及性质;推理能力.
【答案】C
【分析】根据圆内接四边形的对角互补,列式计算即可.
【解答】解:∵四边形ABCD是圆O的内接四边形,
∴∠A+∠C=180°,
∵∠C=110°,
∴∠A=180°﹣∠C=180°﹣110°=70°,
∴∠A的度数为70°,
故选:C.
【点评】本题考查了圆内接四边形的性质,掌握圆内接四边形的性质是解题的关键.
3.(2024秋 包河区校级期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若∠BOD=40°,则∠BAC的度数为( )
A.20° B.50° C.40° D.25°
【考点】圆周角定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】A
【分析】连接OC,利用垂径定理可知,故可得出∠BOD=∠BOC=40°,再由圆周角定理即可得出结论.
【解答】解:连接OC,
∵线段AB是⊙O的直径,弦CD⊥AB于点E.
∴,
∵∠BOD=40°,
∴∠BOD=∠BOC=40°
∴∠BAC∠BOD=20°,
故选:A.
【点评】本题考查的是垂径定理及圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
4.(2024秋 临潼区期末)如图,BC为⊙O的直径,D为的中点,,连接AB和AD,AD交BC于点E,则∠DEC的度数为( )
A.115° B.110° C.105° D.100°
【考点】圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】连接AO,BD,CD,根据圆周角定理得∠BDC=90°,再求出∠C=∠CBD=45°,∠CDE∠AOC=30°,根据三角形内角和定理即可得出答案.
【解答】解:如图,连接AO,BD,CD,
∵BC为⊙O的直径,
∴∠BDC=90°,
∵D为的中点,
∴BD=CD,
∴∠C=∠CBD=45°,
∵,
∴∠AOC180°=60°,
∴∠CDE∠AOC=30°,
∴∠DEC=180°﹣45°﹣30°=105°.
故选:C.
【点评】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
5.(2024秋 长春校级期末)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )
A. B. C. D.
【考点】圆周角定理;解直角三角形.
【专题】圆的有关概念及性质;推理能力.
【答案】D
【分析】接AC、BC,先根据圆周角定理得到∠ACB=90°,∠ADC=∠ABC,在Rt△ACB中,由tan∠ADC=tan∠ABC即可.
【解答】解:连接AC、BC,
∵AB为直径,
∴∠ACB=90°,
∵AC=AC,
∴∠ADC=∠ABC,
在Rt△ACB中,
∵tan∠ABC.
∴tan∠ADC
故选:D.
【点评】本题考查圆周角定理、正切,掌握圆周角定理是解答的关键.
二.填空题(共5小题)
6.(2024秋 清江浦区期末)如图,在⊙O内接四边形ABCD中,若∠D=50°,则∠B= 130 °.
【考点】圆内接四边形的性质;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】130.
【分析】根据圆内接四边形的对角互补计算即可.
【解答】解:∵四边形ABC为圆内接四边形,
∴∠D+∠B=180°,
∵∠D=50°,
∴∠B=180°﹣50°=130°,
故答案为:130.
【点评】本题考查的是圆内接四边形的性质,熟记圆内接四边形对角互补是解题的关键.
7.(2024秋 红花岗区校级期末)如图,四边形ABCD内接于⊙O,∠ACD=15°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径为: .
【考点】圆内接四边形的性质;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】.
【分析】连接BD,依题意得AB是⊙O的直径,过点O作OE⊥BD交AB于点E,则OE是BD的垂直平分线,则∠EDB=∠ABD=15°,进而得∠AED=30°,设AD=a,则DE=BE=2a,AE,AB,再根据AB+AD=2得,则AB,在Rt△ABD中,由勾股定理求出BD,进而可得⊙O的半径.
【解答】解:连接BD,如图1所示:
∵∠ACD=15°,∠BAC=∠CAD=45°,
∴∠ABD=∠ACD=15°,∠BAD=∠BAC+∠CAD=90°,
∴AB是⊙O的直径,
∴OB=OD,
过点O作OE⊥BD交AB于点E,连接DE,如图2所示:
∴OE是BD的垂直平分线,
∴BE=DE,
∴∠EDB=∠ABD=15°,
∴∠AED=∠EDB+∠ABD=30°,
在Rt△AED中,设AD=a,
∴DE=BE=2AD=2a,
由勾股定理得:AE,
∴AB=BE+AE,
∴AB+AD=2,
∴,
∴,
∴AB,
在Rt△ABD中,由勾股定理得:BD,
∴OBBD.
∴⊙O的半径为.
故答案为:.
【点评】此题主要考查了圆内接四边形的性质,圆周角定理,熟练掌握圆内接四边形的性质,圆周角定理,灵活运用含有30°角的直角三角形的性质和勾股定理进行计算还是解决问题的关键.
8.(2024秋 崇川区期末)如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AB=AD.点E在BA的延长线上,若∠EAD=40°,则∠B的度数为 70° .
【考点】圆内接四边形的性质;三角形的外角性质;等腰三角形的性质;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】70°.
【分析】连接OA、OD,根据圆内接四边形的性质求出∠BCD,根据圆周角定理求出∠BOD,进而求出∠BOA,再根据等腰三角形的性质、三角形内角和定理计算即可.
【解答】解:如图,连接OA、OD,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BAD+∠EAD=180°,∠EAD=40°,
∴∠BCD=∠EAD=40°,
∴∠BOD=2∠BCD=80°,
∵AB=AD,
∴,
∴∠BOA=∠DOA=40°,
∵OA=OB,
∴∠B(180°﹣40°)=70°,
故答案为:70°.
【点评】本题考查的是圆内接四边形的性质、圆周角定理,熟记圆内接四边形的对角互补是解题的关键.
9.(2024秋 大足区期末)如图,在⊙O中,∠BCD=120°,半径OF∥AD交AB于点E,若OF=2,AE=2EO,则∠BAD= 60 °;AB= 10 .
【考点】圆周角定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】60;10.
【分析】作OF⊥AB,连接OA,利用圆内接四边形对角互补求出∠BAD,利用平行线得到∠OFE=60°,根据解特殊直角三角形得到三边关系,设EF=x,则AF=5x,OFx,利用勾股定理求出x值继而得到AB长即可.
【解答】解:如图,作OF⊥AB,连接OA,
∵四边形ABCD是圆内接四边形,且∠BCD=120°,
∴∠BAD=180°﹣120°=60°,
∵OF∥AD,
∴∠DAB=∠OFE=60°,
∴EO=2EF,OFEF,
∵AE=2EO,
∴AE=4EF,
设EF=x,则AF=5x,OFx,
在Rt△AFO 中,AO=OF=2,由勾股定理得:
x2+(x)2=(2)2,
解得x(舍去负值),
∴AF=5,
∴AB=2AF=10.
故答案为:60;10.
【点评】本题考查了圆周角定理及垂径定理,熟练掌握以上知识点是关键.
10.(2024秋 丽水期末)如图,C是以AB为直径的半圆O上的一点,且0°<∠ABC<45°,将沿弦BC折叠交AB于点D,E是的中点,连结CE恰好经过圆心O,若AB=2,则AD的长为 .
【考点】圆周角定理;翻折变换(折叠问题);垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;几何直观;运算能力;推理能力.
【答案】.
【分析】连接CD,AC,过点C作CH⊥AB于点H,设弧DE的度数为α,根据折叠的性质及圆周角定理可求出α=22.5°,则∠DCB=45°,∠A=67.5°,∠ADC=67.5°,则AD=2AH,△OCH是等腰直角三角形,即CH=OH,再由勾股定理得OH,进而得AH,据此可得AD的长.
【解答】解:连接CD,AC,过点C作CH⊥AB于点H,如图所示:
∵点E是的中点,
∴,
∴设的度数为α,
则的度数为2α,∠DCE=∠BCE=α,
∵CE恰好经过圆心O,AB=2,
∴OB=OC=OA=1,
∴∠ABC=∠BCE=α,
∴的度数为α,的度数为α,
∴的度数为3α
由折叠的性质得:的度数为3α,
∵的度数为180°,
∴α+3α=180°,
解得:α=22.5°,
∴∠ABC=∠BCE=∠DCE=22.5,
∴∠DCB=∠DCE=∠BCE=45°,
∵AB为半圆O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC=67.5°,
又∵∠ADC=∠DCB+∠ABC=67.5°,
∴AC=CD,
∵CH⊥AB,
∴AH=DH,
∴AD=2AH,
在Rt△OCH中,∠COH=∠ABC+∠BCE=45°,
∴△OCH是等腰直角三角形,即CH=OH,
由勾股定理得:OCOH,
∴OHOC,
∴AH=OA﹣OH,
∴AD=2AH.
【点评】此题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,图形的折叠变换及其性质,理解圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握图形的折叠变换及其性质是解决问题的关键.
三.解答题(共5小题)
11.(2024秋 包河区校级期末)如图,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连接CD,CA,AD,延长AC,DB相交于点E.
(1)求证:AB=BE;
(2)若,BD=6,求直径AB的长.
【考点】圆周角定理;等腰三角形的判定与性质;勾股定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】(1)见解析;
(2)10.
【分析】(1)延长CO交⊙O于点F,连接BC,先根据圆周角定理得出∠ADB=90°,再由点C为的中点可知CF⊥AD,故可得出OC∥BE,再由AO=CO得出∠ACO=∠CAO,故∠CAO=∠E,进而得出结论;
(2)设⊙O的半径为R,则AB=BE=2R,由OA=OB,OC∥BE可知OC是△ABE的中位线,再利用勾股定理求解即可.
【解答】(1)证明:如图,延长CO交⊙O于点F,连接BC.
∵AB为⊙O的直径,
∴∠ADB=90°,即DE⊥AD.
∵点C为的中点,
∴CF⊥AD,
∴OC∥BE,
∴∠ACO=∠E.
∵AO=CO,
∴∠ACO=∠CAO,
∴∠CAO=∠E,
∴AB=BE;
(2)解:设⊙O的半径为R,则AB=BE=2R,
∵BD=6.
∴DE=BD+BE=2R+6.
由(1)知,DE⊥AD,CF⊥AD,
∴OC∥BE,
∵OA=OB,
∴OC是△ABE的中位线,
∴,
∴.
在Rt△ABD 中,由勾股定理得AD2=AB2﹣BD2
在Rt△AED中,由勾股定理得AD2=AE2﹣DE2
∴AB2﹣BD2=AE2﹣DE2,即,
解得R1=5种R2=﹣8不合题意,舍去),
∴AB=2R=2×5=10.
【点评】本题考查的是圆周角定理,垂径定理及勾股定理,等腰三角形的判定与性质,根据题意作出辅助线构造出直角三角形是解题的关键.
12.(2024秋 番禺区期末)如图,⊙O的直径AB的长为10cm,弦AC长为6cm,∠ACB的平分线交⊙O于点D.试求BC,AD的长.
【考点】圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】8cm,5cm.
【分析】连接AD、BD、OD.由圆周角定理可知∠ACB=90°,在Rt△ABC中利用勾股定理求出BC;根据角平分线的定义和圆周角定理得AD=BD,根据等腰三角形的性质得∠AOD=90°,在Rt△AOD中利用勾股定理求出AD即可.
【解答】解:如图,连接AD、BD、OD.
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中利用勾股定理,得BC8(cm);
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD,
∴AD=BD,
∵OA=OB,
∴OD⊥AB,
∴∠AOD=90°,
在Rt△AOD中利用勾股定理,得AD5(cm).
【点评】本题考查圆周角定理,掌握圆周角定理、勾股定理、角平分线的性质、等腰三角形的性质是解题的关键.
13.(2024秋 番禺区期末)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,求∠OAB的度数.
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】34°.
【分析】先利用圆周角定理可得:∠COB=2∠D=56°,然后利用垂径定理可得:,从而可得∠AOC=∠COB=56°,进而可得∠AOB=112°,最后利用等腰三角形的性质以及三角形内角和定理进行计算,即可解答.
【解答】解:∵∠D=28°,
∴∠COB=2∠D=56°,
∵OC⊥AB,
∴,
∴∠AOC=∠COB=56°,
∴∠AOB=∠AOC+∠COB=112°,
∵OA=OB,
∴∠OAB=∠OBA34°.
【点评】本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形进行分析是解题的关键.
14.(2024秋 建邺区期末)如图,在⊙O中,弦AC,BD相交于点M,且AM=BM.求证:CM=DM.
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】证明见解答过程.
【分析】连接CD,根据等腰三角形的性质得到∠A=∠B,根据圆周角定理得到∠D=∠A,∠C=∠B,得到∠C=∠D,根据等腰三角形的判定证明.
【解答】证明:如图,连接CD,
∵AM=BM,
∴∠A=∠B,
由圆周角定理得:∠D=∠A,∠C=∠B,
∴∠C=∠D,
∴CM=DM.
【点评】本题考查的是圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
15.(2024秋 白云区期末)如图,OA、OB、OC都是⊙O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=8,,求⊙O的半径.
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力.
【答案】(1)见解析;
(2)5.
【分析】(1)利用圆周角定理可得,,结合∠ACB=2∠BAC可证明结论;
(2)过点O作半径OD⊥AB于点E,可得AE=BE,根据圆周角、弦、弧的关系可证得BD=BC,即可求得BE=4,DB=2,利用勾股定理可求解DE=2,再利用勾股定理可求解圆的半径.
【解答】(1)证明:∵,,∠ACB=2∠BAC,
∴∠AOB=2∠BOC;
(2)解:过点O作半径OD⊥AB于点E,连接DB,
∴AE=BE,
∵∠AOB=2∠BOC,∠DOB∠AOB,
∴∠DOB=∠BOC.
∴BD=BC.
∵AB=8,BC=2,
∴BE=4,DB=2,
在 Rt△BDE 中,∠DEB=90°,
∴,
在Rt△BOE中,∠OEB=90°,
OB2=(OB﹣2)2+42,
解得OB=5,
即⊙O的半径是5.
【点评】本题主要考查圆周角定理,勾股定理,垂径定理,圆心角、弦、弧的关系,掌握圆周角定理是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 清江浦区期末)如图,∠APB的边交⊙O于A、B、C、D,、、、的度数分别为α、β、γ、θ,若要确定∠APB的大小,则需要确定的弧的度数是( )
A.α、β B.β、γ C.γ、θ D.α、γ
2.(2024秋 济南期末)如图,四边形ABCD是圆O的内接四边形,∠C=110°,则∠A的度数为( )
A.55° B.60° C.70° D.80°
3.(2024秋 包河区校级期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若∠BOD=40°,则∠BAC的度数为( )
A.20° B.50° C.40° D.25°
4.(2024秋 临潼区期末)如图,BC为⊙O的直径,D为的中点,,连接AB和AD,AD交BC于点E,则∠DEC的度数为( )
A.115° B.110° C.105° D.100°
5.(2024秋 长春校级期末)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 清江浦区期末)如图,在⊙O内接四边形ABCD中,若∠D=50°,则∠B= °.
7.(2024秋 红花岗区校级期末)如图,四边形ABCD内接于⊙O,∠ACD=15°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径为: .
8.(2024秋 崇川区期末)如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AB=AD.点E在BA的延长线上,若∠EAD=40°,则∠B的度数为 .
9.(2024秋 大足区期末)如图,在⊙O中,∠BCD=120°,半径OF∥AD交AB于点E,若OF=2,AE=2EO,则∠BAD= °;AB= .
10.(2024秋 丽水期末)如图,C是以AB为直径的半圆O上的一点,且0°<∠ABC<45°,将沿弦BC折叠交AB于点D,E是的中点,连结CE恰好经过圆心O,若AB=2,则AD的长为 .
三.解答题(共5小题)
11.(2024秋 包河区校级期末)如图,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连接CD,CA,AD,延长AC,DB相交于点E.
(1)求证:AB=BE;
(2)若,BD=6,求直径AB的长.
12.(2024秋 番禺区期末)如图,⊙O的直径AB的长为10cm,弦AC长为6cm,∠ACB的平分线交⊙O于点D.试求BC,AD的长.
13.(2024秋 番禺区期末)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,求∠OAB的度数.
14.(2024秋 建邺区期末)如图,在⊙O中,弦AC,BD相交于点M,且AM=BM.求证:CM=DM.
15.(2024秋 白云区期末)如图,OA、OB、OC都是⊙O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=8,,求⊙O的半径.
中考押题卷:圆周角与圆心角的关系
参考答案与试题解析
题号 1 2 3 4 5
答案 D C A C D
一.选择题(共5小题)
1.(2024秋 清江浦区期末)如图,∠APB的边交⊙O于A、B、C、D,、、、的度数分别为α、β、γ、θ,若要确定∠APB的大小,则需要确定的弧的度数是( )
A.α、β B.β、γ C.γ、θ D.α、γ
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】D
【分析】连接BD,根据已知易得:∠ADBα,∠DBCγ,然后利用三角形的外角性质进行计算即可解答.
【解答】解:连接BD,
∵、的度数分别为α、γ,
∴∠ADBα,∠DBCγ,
∵∠ADB是△DBP的一个外角,
∴∠APB=∠ADB﹣∠DBCαγ,
故选:D.
【点评】本题考查了圆周角定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
2.(2024秋 济南期末)如图,四边形ABCD是圆O的内接四边形,∠C=110°,则∠A的度数为( )
A.55° B.60° C.70° D.80°
【考点】圆内接四边形的性质.
【专题】圆的有关概念及性质;推理能力.
【答案】C
【分析】根据圆内接四边形的对角互补,列式计算即可.
【解答】解:∵四边形ABCD是圆O的内接四边形,
∴∠A+∠C=180°,
∵∠C=110°,
∴∠A=180°﹣∠C=180°﹣110°=70°,
∴∠A的度数为70°,
故选:C.
【点评】本题考查了圆内接四边形的性质,掌握圆内接四边形的性质是解题的关键.
3.(2024秋 包河区校级期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若∠BOD=40°,则∠BAC的度数为( )
A.20° B.50° C.40° D.25°
【考点】圆周角定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】A
【分析】连接OC,利用垂径定理可知,故可得出∠BOD=∠BOC=40°,再由圆周角定理即可得出结论.
【解答】解:连接OC,
∵线段AB是⊙O的直径,弦CD⊥AB于点E.
∴,
∵∠BOD=40°,
∴∠BOD=∠BOC=40°
∴∠BAC∠BOD=20°,
故选:A.
【点评】本题考查的是垂径定理及圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
4.(2024秋 临潼区期末)如图,BC为⊙O的直径,D为的中点,,连接AB和AD,AD交BC于点E,则∠DEC的度数为( )
A.115° B.110° C.105° D.100°
【考点】圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】连接AO,BD,CD,根据圆周角定理得∠BDC=90°,再求出∠C=∠CBD=45°,∠CDE∠AOC=30°,根据三角形内角和定理即可得出答案.
【解答】解:如图,连接AO,BD,CD,
∵BC为⊙O的直径,
∴∠BDC=90°,
∵D为的中点,
∴BD=CD,
∴∠C=∠CBD=45°,
∵,
∴∠AOC180°=60°,
∴∠CDE∠AOC=30°,
∴∠DEC=180°﹣45°﹣30°=105°.
故选:C.
【点评】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
5.(2024秋 长春校级期末)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )
A. B. C. D.
【考点】圆周角定理;解直角三角形.
【专题】圆的有关概念及性质;推理能力.
【答案】D
【分析】接AC、BC,先根据圆周角定理得到∠ACB=90°,∠ADC=∠ABC,在Rt△ACB中,由tan∠ADC=tan∠ABC即可.
【解答】解:连接AC、BC,
∵AB为直径,
∴∠ACB=90°,
∵AC=AC,
∴∠ADC=∠ABC,
在Rt△ACB中,
∵tan∠ABC.
∴tan∠ADC
故选:D.
【点评】本题考查圆周角定理、正切,掌握圆周角定理是解答的关键.
二.填空题(共5小题)
6.(2024秋 清江浦区期末)如图,在⊙O内接四边形ABCD中,若∠D=50°,则∠B= 130 °.
【考点】圆内接四边形的性质;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】130.
【分析】根据圆内接四边形的对角互补计算即可.
【解答】解:∵四边形ABC为圆内接四边形,
∴∠D+∠B=180°,
∵∠D=50°,
∴∠B=180°﹣50°=130°,
故答案为:130.
【点评】本题考查的是圆内接四边形的性质,熟记圆内接四边形对角互补是解题的关键.
7.(2024秋 红花岗区校级期末)如图,四边形ABCD内接于⊙O,∠ACD=15°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径为: .
【考点】圆内接四边形的性质;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】.
【分析】连接BD,依题意得AB是⊙O的直径,过点O作OE⊥BD交AB于点E,则OE是BD的垂直平分线,则∠EDB=∠ABD=15°,进而得∠AED=30°,设AD=a,则DE=BE=2a,AE,AB,再根据AB+AD=2得,则AB,在Rt△ABD中,由勾股定理求出BD,进而可得⊙O的半径.
【解答】解:连接BD,如图1所示:
∵∠ACD=15°,∠BAC=∠CAD=45°,
∴∠ABD=∠ACD=15°,∠BAD=∠BAC+∠CAD=90°,
∴AB是⊙O的直径,
∴OB=OD,
过点O作OE⊥BD交AB于点E,连接DE,如图2所示:
∴OE是BD的垂直平分线,
∴BE=DE,
∴∠EDB=∠ABD=15°,
∴∠AED=∠EDB+∠ABD=30°,
在Rt△AED中,设AD=a,
∴DE=BE=2AD=2a,
由勾股定理得:AE,
∴AB=BE+AE,
∴AB+AD=2,
∴,
∴,
∴AB,
在Rt△ABD中,由勾股定理得:BD,
∴OBBD.
∴⊙O的半径为.
故答案为:.
【点评】此题主要考查了圆内接四边形的性质,圆周角定理,熟练掌握圆内接四边形的性质,圆周角定理,灵活运用含有30°角的直角三角形的性质和勾股定理进行计算还是解决问题的关键.
8.(2024秋 崇川区期末)如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AB=AD.点E在BA的延长线上,若∠EAD=40°,则∠B的度数为 70° .
【考点】圆内接四边形的性质;三角形的外角性质;等腰三角形的性质;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】70°.
【分析】连接OA、OD,根据圆内接四边形的性质求出∠BCD,根据圆周角定理求出∠BOD,进而求出∠BOA,再根据等腰三角形的性质、三角形内角和定理计算即可.
【解答】解:如图,连接OA、OD,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BAD+∠EAD=180°,∠EAD=40°,
∴∠BCD=∠EAD=40°,
∴∠BOD=2∠BCD=80°,
∵AB=AD,
∴,
∴∠BOA=∠DOA=40°,
∵OA=OB,
∴∠B(180°﹣40°)=70°,
故答案为:70°.
【点评】本题考查的是圆内接四边形的性质、圆周角定理,熟记圆内接四边形的对角互补是解题的关键.
9.(2024秋 大足区期末)如图,在⊙O中,∠BCD=120°,半径OF∥AD交AB于点E,若OF=2,AE=2EO,则∠BAD= 60 °;AB= 10 .
【考点】圆周角定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】60;10.
【分析】作OF⊥AB,连接OA,利用圆内接四边形对角互补求出∠BAD,利用平行线得到∠OFE=60°,根据解特殊直角三角形得到三边关系,设EF=x,则AF=5x,OFx,利用勾股定理求出x值继而得到AB长即可.
【解答】解:如图,作OF⊥AB,连接OA,
∵四边形ABCD是圆内接四边形,且∠BCD=120°,
∴∠BAD=180°﹣120°=60°,
∵OF∥AD,
∴∠DAB=∠OFE=60°,
∴EO=2EF,OFEF,
∵AE=2EO,
∴AE=4EF,
设EF=x,则AF=5x,OFx,
在Rt△AFO 中,AO=OF=2,由勾股定理得:
x2+(x)2=(2)2,
解得x(舍去负值),
∴AF=5,
∴AB=2AF=10.
故答案为:60;10.
【点评】本题考查了圆周角定理及垂径定理,熟练掌握以上知识点是关键.
10.(2024秋 丽水期末)如图,C是以AB为直径的半圆O上的一点,且0°<∠ABC<45°,将沿弦BC折叠交AB于点D,E是的中点,连结CE恰好经过圆心O,若AB=2,则AD的长为 .
【考点】圆周角定理;翻折变换(折叠问题);垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;几何直观;运算能力;推理能力.
【答案】.
【分析】连接CD,AC,过点C作CH⊥AB于点H,设弧DE的度数为α,根据折叠的性质及圆周角定理可求出α=22.5°,则∠DCB=45°,∠A=67.5°,∠ADC=67.5°,则AD=2AH,△OCH是等腰直角三角形,即CH=OH,再由勾股定理得OH,进而得AH,据此可得AD的长.
【解答】解:连接CD,AC,过点C作CH⊥AB于点H,如图所示:
∵点E是的中点,
∴,
∴设的度数为α,
则的度数为2α,∠DCE=∠BCE=α,
∵CE恰好经过圆心O,AB=2,
∴OB=OC=OA=1,
∴∠ABC=∠BCE=α,
∴的度数为α,的度数为α,
∴的度数为3α
由折叠的性质得:的度数为3α,
∵的度数为180°,
∴α+3α=180°,
解得:α=22.5°,
∴∠ABC=∠BCE=∠DCE=22.5,
∴∠DCB=∠DCE=∠BCE=45°,
∵AB为半圆O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC=67.5°,
又∵∠ADC=∠DCB+∠ABC=67.5°,
∴AC=CD,
∵CH⊥AB,
∴AH=DH,
∴AD=2AH,
在Rt△OCH中,∠COH=∠ABC+∠BCE=45°,
∴△OCH是等腰直角三角形,即CH=OH,
由勾股定理得:OCOH,
∴OHOC,
∴AH=OA﹣OH,
∴AD=2AH.
【点评】此题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,图形的折叠变换及其性质,理解圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握图形的折叠变换及其性质是解决问题的关键.
三.解答题(共5小题)
11.(2024秋 包河区校级期末)如图,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连接CD,CA,AD,延长AC,DB相交于点E.
(1)求证:AB=BE;
(2)若,BD=6,求直径AB的长.
【考点】圆周角定理;等腰三角形的判定与性质;勾股定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】(1)见解析;
(2)10.
【分析】(1)延长CO交⊙O于点F,连接BC,先根据圆周角定理得出∠ADB=90°,再由点C为的中点可知CF⊥AD,故可得出OC∥BE,再由AO=CO得出∠ACO=∠CAO,故∠CAO=∠E,进而得出结论;
(2)设⊙O的半径为R,则AB=BE=2R,由OA=OB,OC∥BE可知OC是△ABE的中位线,再利用勾股定理求解即可.
【解答】(1)证明:如图,延长CO交⊙O于点F,连接BC.
∵AB为⊙O的直径,
∴∠ADB=90°,即DE⊥AD.
∵点C为的中点,
∴CF⊥AD,
∴OC∥BE,
∴∠ACO=∠E.
∵AO=CO,
∴∠ACO=∠CAO,
∴∠CAO=∠E,
∴AB=BE;
(2)解:设⊙O的半径为R,则AB=BE=2R,
∵BD=6.
∴DE=BD+BE=2R+6.
由(1)知,DE⊥AD,CF⊥AD,
∴OC∥BE,
∵OA=OB,
∴OC是△ABE的中位线,
∴,
∴.
在Rt△ABD 中,由勾股定理得AD2=AB2﹣BD2
在Rt△AED中,由勾股定理得AD2=AE2﹣DE2
∴AB2﹣BD2=AE2﹣DE2,即,
解得R1=5种R2=﹣8不合题意,舍去),
∴AB=2R=2×5=10.
【点评】本题考查的是圆周角定理,垂径定理及勾股定理,等腰三角形的判定与性质,根据题意作出辅助线构造出直角三角形是解题的关键.
12.(2024秋 番禺区期末)如图,⊙O的直径AB的长为10cm,弦AC长为6cm,∠ACB的平分线交⊙O于点D.试求BC,AD的长.
【考点】圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】8cm,5cm.
【分析】连接AD、BD、OD.由圆周角定理可知∠ACB=90°,在Rt△ABC中利用勾股定理求出BC;根据角平分线的定义和圆周角定理得AD=BD,根据等腰三角形的性质得∠AOD=90°,在Rt△AOD中利用勾股定理求出AD即可.
【解答】解:如图,连接AD、BD、OD.
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中利用勾股定理,得BC8(cm);
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD,
∴AD=BD,
∵OA=OB,
∴OD⊥AB,
∴∠AOD=90°,
在Rt△AOD中利用勾股定理,得AD5(cm).
【点评】本题考查圆周角定理,掌握圆周角定理、勾股定理、角平分线的性质、等腰三角形的性质是解题的关键.
13.(2024秋 番禺区期末)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,求∠OAB的度数.
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】34°.
【分析】先利用圆周角定理可得:∠COB=2∠D=56°,然后利用垂径定理可得:,从而可得∠AOC=∠COB=56°,进而可得∠AOB=112°,最后利用等腰三角形的性质以及三角形内角和定理进行计算,即可解答.
【解答】解:∵∠D=28°,
∴∠COB=2∠D=56°,
∵OC⊥AB,
∴,
∴∠AOC=∠COB=56°,
∴∠AOB=∠AOC+∠COB=112°,
∵OA=OB,
∴∠OAB=∠OBA34°.
【点评】本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形进行分析是解题的关键.
14.(2024秋 建邺区期末)如图,在⊙O中,弦AC,BD相交于点M,且AM=BM.求证:CM=DM.
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】证明见解答过程.
【分析】连接CD,根据等腰三角形的性质得到∠A=∠B,根据圆周角定理得到∠D=∠A,∠C=∠B,得到∠C=∠D,根据等腰三角形的判定证明.
【解答】证明:如图,连接CD,
∵AM=BM,
∴∠A=∠B,
由圆周角定理得:∠D=∠A,∠C=∠B,
∴∠C=∠D,
∴CM=DM.
【点评】本题考查的是圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
15.(2024秋 白云区期末)如图,OA、OB、OC都是⊙O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=8,,求⊙O的半径.
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力.
【答案】(1)见解析;
(2)5.
【分析】(1)利用圆周角定理可得,,结合∠ACB=2∠BAC可证明结论;
(2)过点O作半径OD⊥AB于点E,可得AE=BE,根据圆周角、弦、弧的关系可证得BD=BC,即可求得BE=4,DB=2,利用勾股定理可求解DE=2,再利用勾股定理可求解圆的半径.
【解答】(1)证明:∵,,∠ACB=2∠BAC,
∴∠AOB=2∠BOC;
(2)解:过点O作半径OD⊥AB于点E,连接DB,
∴AE=BE,
∵∠AOB=2∠BOC,∠DOB∠AOB,
∴∠DOB=∠BOC.
∴BD=BC.
∵AB=8,BC=2,
∴BE=4,DB=2,
在 Rt△BDE 中,∠DEB=90°,
∴,
在Rt△BOE中,∠OEB=90°,
OB2=(OB﹣2)2+42,
解得OB=5,
即⊙O的半径是5.
【点评】本题主要考查圆周角定理,勾股定理,垂径定理,圆心角、弦、弧的关系,掌握圆周角定理是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
