【中考押题卷】2025年北师大版中考数学考前冲刺:弧长与扇形的面积(含解析)
文档属性
| 名称 | 【中考押题卷】2025年北师大版中考数学考前冲刺:弧长与扇形的面积(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:18:16 | ||
图片预览


文档简介
中考押题卷:弧长与扇形的面积
一.选择题(共5小题)
1.(2025 柳州一模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
2.(2024秋 扬州期末)已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
3.(2024秋 南川区期末)如图,在Rt△ABC中,∠C=90°,AB=4,BC=2.以点C为圆心,CB长为半径画弧,分别交AB,AC于点E,D,则图中阴影部分的面积为( )
A. B. C. D.
4.(2024秋 普陀区期末)如图,将△ABC绕点B逆时针旋转n°后得到△A1BC1,其中点A、C分别与点A1、C1对应,AC与A1B交于点O,那么下列说法中错误的是( )
A.AB=A1B
B.∠ABA1=∠CBC1
C.阴影部分的面积与△ABA1的面积相等
D.△AA1O与△BCO的面积相等
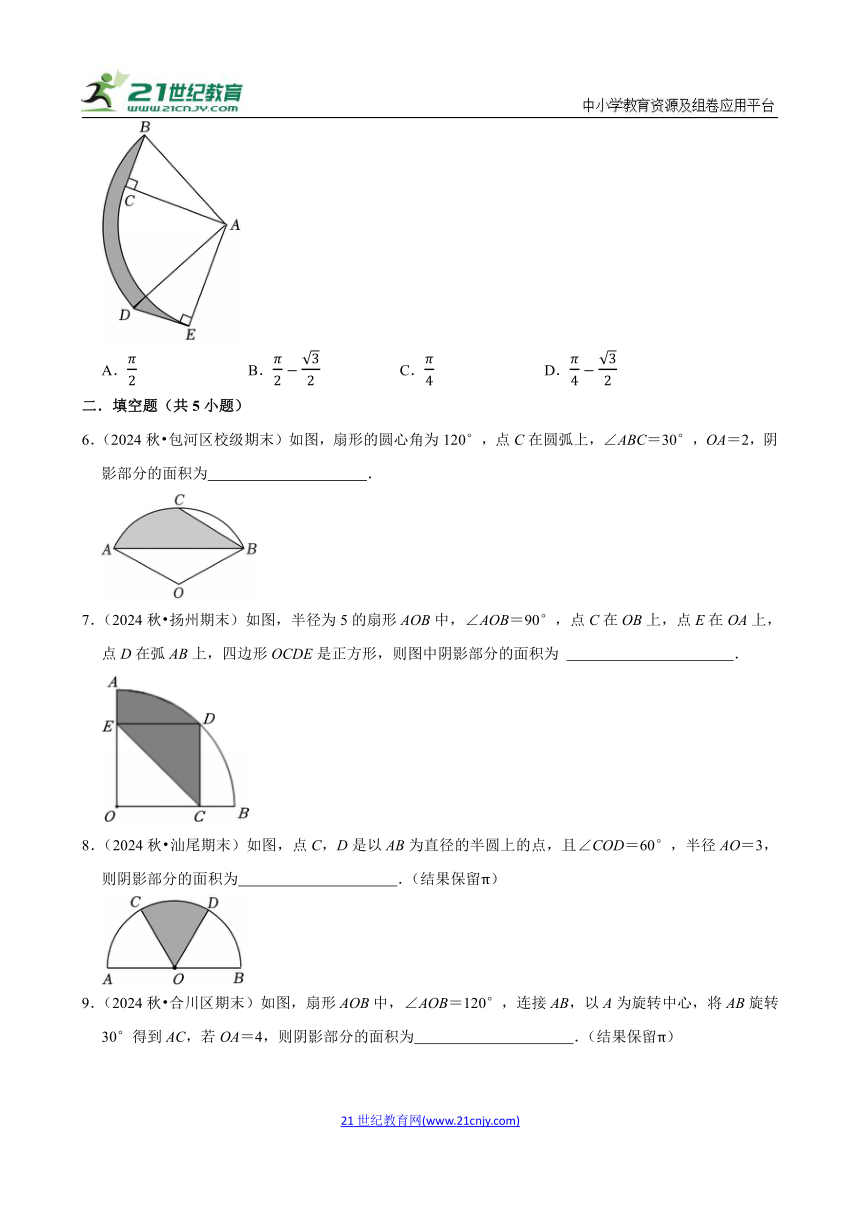
5.(2024秋 廉江市期末)如图,在△ABC中,∠ACB=90°,BC=1,AC,将△ABC绕着点A逆时针旋转90°得到△ADE,则图中阴影部分的面积是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 包河区校级期末)如图,扇形的圆心角为120°,点C在圆弧上,∠ABC=30°,OA=2,阴影部分的面积为 .
7.(2024秋 扬州期末)如图,半径为5的扇形AOB中,∠AOB=90°,点C在OB上,点E在OA上,点D在弧AB上,四边形OCDE是正方形,则图中阴影部分的面积为 .
8.(2024秋 汕尾期末)如图,点C,D是以AB为直径的半圆上的点,且∠COD=60°,半径AO=3,则阴影部分的面积为 .(结果保留π)
9.(2024秋 合川区期末)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=4,则阴影部分的面积为 .(结果保留π)
10.(2024秋 番禺区期末)如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为 .
三.解答题(共5小题)
11.(2024秋 盐城期末)如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC,AC分别相交于点D,E.
(1)求证:BD=CD;
(2)若⊙O半径为5,∠CDE=50°,求扇形ODB的面积.
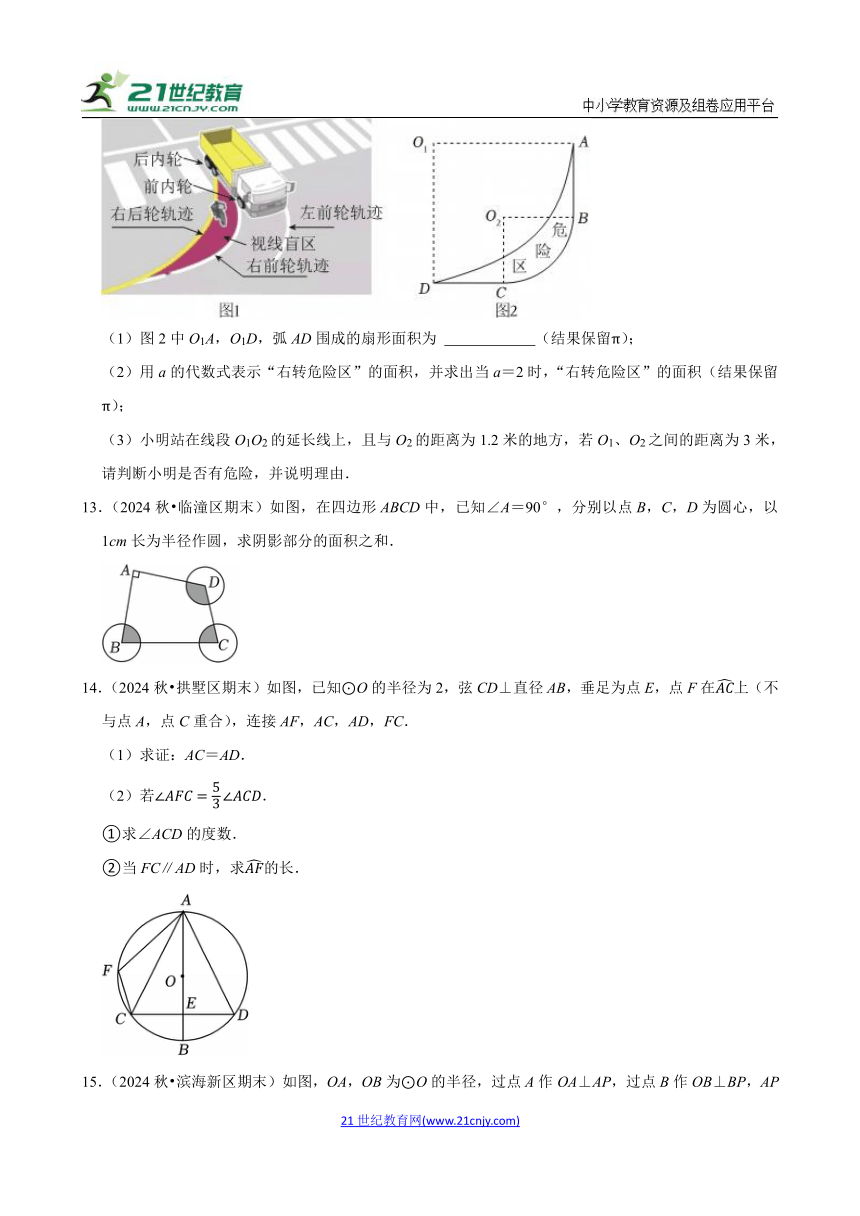
12.(2024秋 江都区期末)汽车盲区是造成交通事故的罪魁祸首之一,它是指驾驶员位于正常驾驶座位置,其视线被车体遮挡而不能直接观察到的那部分区域.如图1,有一种汽车盲区叫做内轮差盲区,内轮差是车辆在转弯时前内轮转弯半径与后内轮转弯半径之差,由于内轮差的存在,汽车在转弯时都会产生这种盲区.为了安全,许多路口都设置“右转危险区”标线.图2是货车在路口“右转危险区”的示意图,后内轮转弯半径O1A=O1D=4米,前内轮转弯半径O2B=O2C=a米,∠DO1A=∠CO2B=90°.
(1)图2中O1A,O1D,弧AD围成的扇形面积为 (结果保留π);
(2)用a的代数式表示“右转危险区”的面积,并求出当a=2时,“右转危险区”的面积(结果保留π);
(3)小明站在线段O1O2的延长线上,且与O2的距离为1.2米的地方,若O1、O2之间的距离为3米,请判断小明是否有危险,并说明理由.
13.(2024秋 临潼区期末)如图,在四边形ABCD中,已知∠A=90°,分别以点B,C,D为圆心,以1cm长为半径作圆,求阴影部分的面积之和.
14.(2024秋 拱墅区期末)如图,已知⊙O的半径为2,弦CD⊥直径AB,垂足为点E,点F在上(不与点A,点C重合),连接AF,AC,AD,FC.
(1)求证:AC=AD.
(2)若.
①求∠ACD的度数.
②当FC∥AD时,求的长.
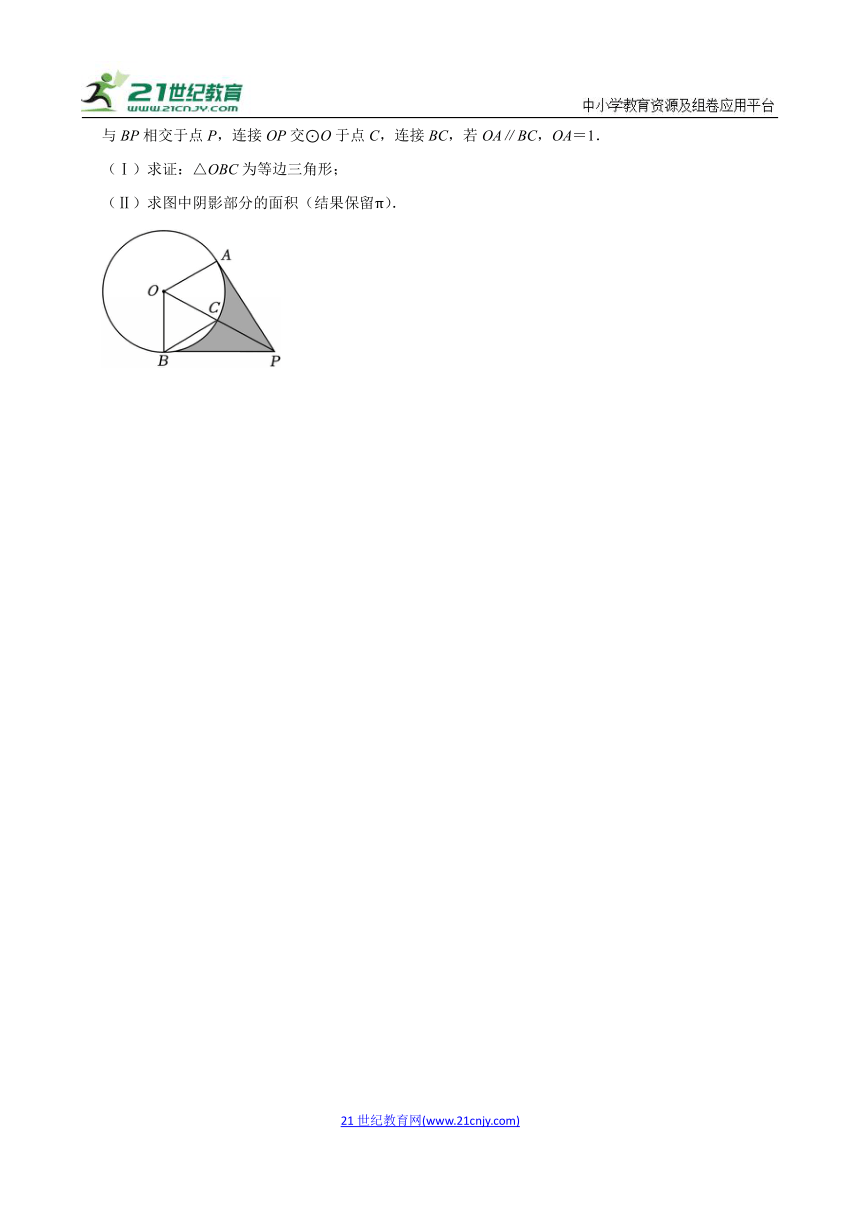
15.(2024秋 滨海新区期末)如图,OA,OB为⊙O的半径,过点A作OA⊥AP,过点B作OB⊥BP,AP与BP相交于点P,连接OP交⊙O于点C,连接BC,若OA∥BC,OA=1.
(Ⅰ)求证:△OBC为等边三角形;
(Ⅱ)求图中阴影部分的面积(结果保留π).
中考押题卷:弧长与扇形的面积
参考答案与试题解析
一.选择题(共5小题)
1.(2025 柳州一模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
【考点】扇形面积的计算.
【答案】C
【分析】直接代入扇形的面积公式即可得出答案.
【解答】解:S扇形3π.
故选:C.
【点评】本题考查了扇形的面积公式,属于基础题,解答本题的关键是熟练掌握扇形的面积公式:S.
2.(2024秋 扬州期末)已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
【考点】弧长的计算.
【答案】D
【分析】把扇形的圆心角为和半径为代入弧长公式计算即可.
【解答】解:依题意,n=60,r=12,
∴扇形的弧长4π.
故选:D.
【点评】本题考查了弧长公式的运用.关键是熟悉公式:扇形的弧长.
3.(2024秋 南川区期末)如图,在Rt△ABC中,∠C=90°,AB=4,BC=2.以点C为圆心,CB长为半径画弧,分别交AB,AC于点E,D,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;勾股定理.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】连接CE,作EF⊥BC于点F,根据题意得出,CB=CE,得到∠B=60°,可得△BCE是等边三角形,计算S阴=S扇BCE﹣S△BCE即可得到答案.
【解答】解:如图,连接CE,作EF⊥BC于点F,
由条件可知,
∴∠B=60°,
∵CB=CE,
∴△BCE是等边三角形,
∴BE=BC=2,
∴,
∴,
∴,
∴,
故选:C.
【点评】本题考查了扇形面积公式及计算,锐角三角函数,等边三角形的判定和性质,熟练掌握相关知识点是解题的关键.
4.(2024秋 普陀区期末)如图,将△ABC绕点B逆时针旋转n°后得到△A1BC1,其中点A、C分别与点A1、C1对应,AC与A1B交于点O,那么下列说法中错误的是( )
A.AB=A1B
B.∠ABA1=∠CBC1
C.阴影部分的面积与△ABA1的面积相等
D.△AA1O与△BCO的面积相等
【考点】扇形面积的计算;旋转的性质;三角形的面积.
【专题】三角形;平移、旋转与对称;推理能力.
【答案】D
【分析】AB.根据旋转的性质判断即可;
C.设△A1BC1中阴影部分的面积为S1,由S△AOB+S△BOC=S△BOC+S1,得S△AOB=S1,从而得S阴影S1S△AOB;
D.S△AOB,S△BCO+S△AOB=S△ABC,由于S△ABC不一定成立,故S△BCO不一定成立.
【解答】解:根据旋转的性质,AB=A1B,∠ABA1=∠CBC1=n°,
∴AB正确,不符合题意;
设△A1BC1中阴影部分的面积为S1,
∵S△AOB+S△BOC=S△BOC+S1,
∴S△AOB=S1,
∴S阴影S1S△AOB,
∴C正确,不符合题意;
S△AOB,S△BCO+S△AOB=S△ABC,
∵S△ABC不一定成立,
∴S△BCO不一定成立,
∴D错误,符合题意.
故选:D.
【点评】本题考查三角形的面积、旋转的性质,掌握旋转的性质是解题的关键.
5.(2024秋 廉江市期末)如图,在△ABC中,∠ACB=90°,BC=1,AC,将△ABC绕着点A逆时针旋转90°得到△ADE,则图中阴影部分的面积是( )
A. B. C. D.
【考点】扇形面积的计算;旋转的性质;勾股定理.
【专题】平移、旋转与对称;与圆有关的计算;运算能力.
【答案】C
【分析】先利用勾股定理求出AB的长,再根据S阴影=S扇形BAD+S△ADE﹣S扇形ACE﹣S△ABC进行求解即可.
【解答】解:由勾股定理得:,
由旋转的性质可得S△ADE=S△ABC,∠BAD=∠CAE=90°,
∴S阴影=S扇形BAD+S△ADE﹣S扇形CAE﹣S△ABC
=S扇形BAD﹣S扇形CAE
,
故选:C.
【点评】本题主要考查了扇形面积计算,勾股定理,熟练掌握以上知识点是解题的关键.
二.填空题(共5小题)
6.(2024秋 包河区校级期末)如图,扇形的圆心角为120°,点C在圆弧上,∠ABC=30°,OA=2,阴影部分的面积为 .
【考点】扇形面积的计算;圆周角定理.
【专题】运算能力.
【答案】.
【分析】连接OC,AC,由∠ABC的度数得出∠AOC的度数,再将阴影部分的面积转化为扇形OAC的面积,最后根据扇形的面积公式即可解决问题.
【解答】解:连接OA,OC,
∵∠ABC=30°,
∴∠AOC=2×30°=60°.
又∵OA=OC,
∴∠OAC=∠OCA=60°.
∵∠AOB=120°,
∴∠COB=120°﹣60°=60°,
∴∠ACO=∠COB,
∴AC∥OB,
∴S△AOC=S△ABC,
∴S阴影=S扇形OAC.
∵OA=2,
∴,
∴.
故答案为:.
【点评】本题主要考查了扇形面积的计算及圆周角定理,熟知圆周角定理及扇形的面积公式是解题的关键.
7.(2024秋 扬州期末)如图,半径为5的扇形AOB中,∠AOB=90°,点C在OB上,点E在OA上,点D在弧AB上,四边形OCDE是正方形,则图中阴影部分的面积为 .
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD,交CE于点F.由正方形的性质得出S△OEF=S△FCD,∠EOD=45°.即根据扇形面积公式求出扇形AOD的面积即可.
【解答】解:如图,连接OD,交CE于点F.
∵四边形OCDE是正方形,
∴S△OEF=S△FCD,∠EOD=45°,
∴S阴=S扇形AOD.
故答案为:.
【点评】本题考查正方形的性质,扇形的面积公式.理解S阴=S扇形AOD是解题关键.
8.(2024秋 汕尾期末)如图,点C,D是以AB为直径的半圆上的点,且∠COD=60°,半径AO=3,则阴影部分的面积为 .(结果保留π)
【考点】扇形面积的计算.
【专题】运算能力.
【答案】.
【分析】直接运用扇形面积公式求解即可.
【解答】解:根据扇形的面积公式得阴影部分的面积为:.
故答案为:.
【点评】本题主要考查求扇形的面积,掌握扇形的面积公式是解题的关键.
9.(2024秋 合川区期末)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=4,则阴影部分的面积为 .(结果保留π)
【考点】扇形面积的计算;旋转的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD交AB于E,先证明△OAD是等边三角形,∠AOD=∠BOD=60°,从而得到OD⊥AB,AB=2AE,继而求得,,即可由S阴影=S扇形BAC﹣S△ABD,求解.
【解答】解:连接OD交AB于E,
∵∠AOB=120°,OA=OB,
∴∠ABO=∠BAO=∠BAC=30°,
∴∠OAD=60°,
∵OA=OD,
∴∠AOD=60°,AD=OA=4,
∴∠BOD=∠AOB﹣∠AOD=60°,
∴∠BOD=∠AOD,
∴OD⊥AB,AB=2AE,
∴,
∴,
∴,
∴.
故答案为:.
【点评】本题考查了扇形的面积,等边三角形的性质和判定,直角三角形的性质,勾股定理等知识点,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.
10.(2024秋 番禺区期末)如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为 2π .
【考点】弧长的计算;等边三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】2π.
【分析】利用弧长计算公式计算即可.
【解答】解:,
∴C=3l=2π,
故答案为:2π.
【点评】本题考查了弧长的计算,等边三角形的性质,掌握弧长的计算公式是解题的关键.
三.解答题(共5小题)
11.(2024秋 盐城期末)如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC,AC分别相交于点D,E.
(1)求证:BD=CD;
(2)若⊙O半径为5,∠CDE=50°,求扇形ODB的面积.
【考点】扇形面积的计算;等腰三角形的性质;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;推理能力.
【答案】(1)见解析;
(2).
【分析】(1)连接AD,根据圆周角定理的推论得到∠BDA=90°,再根据等腰三角形的性质即可得到BD=CD;
(2)根据已知求出∠BOD=50°,根据扇形面积公式即可得到答案.
【解答】(1)证明:连接AD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∴AD⊥BC.
∵AB=AC.
∴BD=CD;
(2)解:∵∠CDE=50°,
∴∠BAC=50°,
∵AD⊥BC.AB=AC.
∴∠BAD=∠CAD=25°,
∴∠BOD=2∠BAD=50°,
∵⊙O半径为5,
∴S扇形ODB.
【点评】本题考查了扇形面积和等腰三角形的性质以及圆周角定理.掌握扇形的面积公式、等腰三角形的性质以及圆周角定理是解题的关键.
12.(2024秋 江都区期末)汽车盲区是造成交通事故的罪魁祸首之一,它是指驾驶员位于正常驾驶座位置,其视线被车体遮挡而不能直接观察到的那部分区域.如图1,有一种汽车盲区叫做内轮差盲区,内轮差是车辆在转弯时前内轮转弯半径与后内轮转弯半径之差,由于内轮差的存在,汽车在转弯时都会产生这种盲区.为了安全,许多路口都设置“右转危险区”标线.图2是货车在路口“右转危险区”的示意图,后内轮转弯半径O1A=O1D=4米,前内轮转弯半径O2B=O2C=a米,∠DO1A=∠CO2B=90°.
(1)图2中O1A,O1D,弧AD围成的扇形面积为 4π平方米 (结果保留π);
(2)用a的代数式表示“右转危险区”的面积,并求出当a=2时,“右转危险区”的面积(结果保留π);
(3)小明站在线段O1O2的延长线上,且与O2的距离为1.2米的地方,若O1、O2之间的距离为3米,请判断小明是否有危险,并说明理由.
【考点】扇形面积的计算;圆周角定理.
【专题】与圆有关的计算;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)4π平方米;
(2)S危险区域=(16﹣4π﹣a2πa2)平方米,
当a=2时,S危险区域=(12﹣3π)平方米;
(3)有危险.
【分析】(1)根据扇形面积的计算公式进行计算即可;
(2)根据正方形面积,扇形面积的计算方法以及图形中各个部分面积之间的关系进行计算即可;
(3)根据图形的对称性,求出小正方形的边长,即小扇形的半径,再根据小扇形半径与1.2的大小关系进行判断即可.
【解答】解:(1)图中O1A,O1D,弧AD围成的扇形面积为4π(平方米),
故答案为:4π平方米;
(2)图中O2C,O2B,弧BC围成的扇形面积为πa2(平方米),
∴S危险区域=(42﹣4π)﹣(a2πa2)
=(16﹣4π﹣a2πa2)平方米,
当a=2时,S危险区域=16﹣4π﹣4+π=(12﹣3π)平方米,
(3)有危险,理由:
如图,连接O1O2并延长一定过点E,则O2E=43,
∴O2C(43),
∵1.75>1.2,
∴有危险.
【点评】本题考查扇形面积的计算,掌握正方形、扇形面积的计算方法是正确解答的关键.
13.(2024秋 临潼区期末)如图,在四边形ABCD中,已知∠A=90°,分别以点B,C,D为圆心,以1cm长为半径作圆,求阴影部分的面积之和.
【考点】扇形面积的计算;三角形的面积.
【专题】与圆有关的计算;运算能力.
【答案】π.
【分析】阴影部分面积之和等于三个扇形面积之和,利用扇形面积公式求解.
【解答】解:⊙B,⊙C,⊙D半径相同,
∴阴影部分面积之和等于三个扇形面积之和,
∵∠A=90°,
∴∠B+∠C+∠D=360°﹣90°=270°,
∴π.
【点评】本题考查扇形面积的计算,三角形的面积,解题的关键是理解题意,灵活运用所学知识解决问题.
14.(2024秋 拱墅区期末)如图,已知⊙O的半径为2,弦CD⊥直径AB,垂足为点E,点F在上(不与点A,点C重合),连接AF,AC,AD,FC.
(1)求证:AC=AD.
(2)若.
①求∠ACD的度数.
②当FC∥AD时,求的长.
【考点】弧长的计算;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1)见解答;
(2)①
②π.
【分析】(1)根据垂径定理及圆心角定理证明;
(2)①根据圆内接四边形的性质求解;
②根据“平行弦所夹的弧相等”,及弧长公式求解.
【解答】(1)证明:∵弦CD⊥直径AB,
∴A平分,即,
∴AC=AD;
(2)①∵四边形AFCD内接于⊙O,
∴∠AFC+∠ADC=180°①,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC②,
由①②得:∠ADC=67.5°,∠AFC=112.5°,
∴∠ACD=67.5°;
②连接OC,OD,
∵∠ADC=∠ACD=67.5°,
∴∠CAD=180°﹣2×67.5°=45°,
∴∠COD=90°,
∵FC∥AD,
∴,
∵的长为:π,
∴的长为π.
【点评】本题考查了弧长公式及垂径定理,掌握弧长公式和垂径定理是解题的关键.
15.(2024秋 滨海新区期末)如图,OA,OB为⊙O的半径,过点A作OA⊥AP,过点B作OB⊥BP,AP与BP相交于点P,连接OP交⊙O于点C,连接BC,若OA∥BC,OA=1.
(Ⅰ)求证:△OBC为等边三角形;
(Ⅱ)求图中阴影部分的面积(结果保留π).
【考点】扇形面积的计算;等边三角形的判定与性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】(Ⅰ)证明见解答;
(Ⅱ).
【分析】(Ⅰ)根据全等三角形的判定与性质、平行线的性质和等边三角形的判定定理证明即可;
(Ⅱ)利用特殊角的三角形函数和三角形面积公式求出S四边形OAPB,利用扇形面积公式求出S扇形AOB,再由S阴影=S四边形OAPB﹣S扇形AOB计算阴影部分的面积即可.
【解答】(Ⅰ)证明:在Rt△OAP和Rt△OBP中,
,
∴Rt△OAP≌Rt△OBP(HL),
∴∠AOP=∠BOP,
∵OA∥BC,
∴∠BCO=∠AOP,
∴∠BOP=∠BCO,
∵OB=OC,
∴∠OBC=∠BCO,
∴∠OBC=∠BCO=∠BOP,
∴△OBC为等边三角形.
(Ⅱ)∵△OBC为等边三角形,
∴∠BOP=60°,
∴BP=OB tan∠BOP=1,
∴SRt△OBP=SRt△OAPOB BP1,
∴S四边形OAPB=SRt△OBP+SRt△OAP,
∵∠AOB=2∠BOP=120°,
∴S扇形AOBπ×12,
∴S阴影=S四边形OAPB﹣S扇形AOB.
【点评】本题考查扇形面积的计算、等边三角形的判定与性质,掌握扇形面积的计算公式、等边三角形的判定与性质、等三角形的判定与性质、平行线的性质、特殊角的三角形函数和三角形面积公式是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2025 柳州一模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
2.(2024秋 扬州期末)已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
3.(2024秋 南川区期末)如图,在Rt△ABC中,∠C=90°,AB=4,BC=2.以点C为圆心,CB长为半径画弧,分别交AB,AC于点E,D,则图中阴影部分的面积为( )
A. B. C. D.
4.(2024秋 普陀区期末)如图,将△ABC绕点B逆时针旋转n°后得到△A1BC1,其中点A、C分别与点A1、C1对应,AC与A1B交于点O,那么下列说法中错误的是( )
A.AB=A1B
B.∠ABA1=∠CBC1
C.阴影部分的面积与△ABA1的面积相等
D.△AA1O与△BCO的面积相等
5.(2024秋 廉江市期末)如图,在△ABC中,∠ACB=90°,BC=1,AC,将△ABC绕着点A逆时针旋转90°得到△ADE,则图中阴影部分的面积是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 包河区校级期末)如图,扇形的圆心角为120°,点C在圆弧上,∠ABC=30°,OA=2,阴影部分的面积为 .
7.(2024秋 扬州期末)如图,半径为5的扇形AOB中,∠AOB=90°,点C在OB上,点E在OA上,点D在弧AB上,四边形OCDE是正方形,则图中阴影部分的面积为 .
8.(2024秋 汕尾期末)如图,点C,D是以AB为直径的半圆上的点,且∠COD=60°,半径AO=3,则阴影部分的面积为 .(结果保留π)
9.(2024秋 合川区期末)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=4,则阴影部分的面积为 .(结果保留π)
10.(2024秋 番禺区期末)如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为 .
三.解答题(共5小题)
11.(2024秋 盐城期末)如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC,AC分别相交于点D,E.
(1)求证:BD=CD;
(2)若⊙O半径为5,∠CDE=50°,求扇形ODB的面积.
12.(2024秋 江都区期末)汽车盲区是造成交通事故的罪魁祸首之一,它是指驾驶员位于正常驾驶座位置,其视线被车体遮挡而不能直接观察到的那部分区域.如图1,有一种汽车盲区叫做内轮差盲区,内轮差是车辆在转弯时前内轮转弯半径与后内轮转弯半径之差,由于内轮差的存在,汽车在转弯时都会产生这种盲区.为了安全,许多路口都设置“右转危险区”标线.图2是货车在路口“右转危险区”的示意图,后内轮转弯半径O1A=O1D=4米,前内轮转弯半径O2B=O2C=a米,∠DO1A=∠CO2B=90°.
(1)图2中O1A,O1D,弧AD围成的扇形面积为 (结果保留π);
(2)用a的代数式表示“右转危险区”的面积,并求出当a=2时,“右转危险区”的面积(结果保留π);
(3)小明站在线段O1O2的延长线上,且与O2的距离为1.2米的地方,若O1、O2之间的距离为3米,请判断小明是否有危险,并说明理由.
13.(2024秋 临潼区期末)如图,在四边形ABCD中,已知∠A=90°,分别以点B,C,D为圆心,以1cm长为半径作圆,求阴影部分的面积之和.
14.(2024秋 拱墅区期末)如图,已知⊙O的半径为2,弦CD⊥直径AB,垂足为点E,点F在上(不与点A,点C重合),连接AF,AC,AD,FC.
(1)求证:AC=AD.
(2)若.
①求∠ACD的度数.
②当FC∥AD时,求的长.
15.(2024秋 滨海新区期末)如图,OA,OB为⊙O的半径,过点A作OA⊥AP,过点B作OB⊥BP,AP与BP相交于点P,连接OP交⊙O于点C,连接BC,若OA∥BC,OA=1.
(Ⅰ)求证:△OBC为等边三角形;
(Ⅱ)求图中阴影部分的面积(结果保留π).
中考押题卷:弧长与扇形的面积
参考答案与试题解析
一.选择题(共5小题)
1.(2025 柳州一模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
【考点】扇形面积的计算.
【答案】C
【分析】直接代入扇形的面积公式即可得出答案.
【解答】解:S扇形3π.
故选:C.
【点评】本题考查了扇形的面积公式,属于基础题,解答本题的关键是熟练掌握扇形的面积公式:S.
2.(2024秋 扬州期末)已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
【考点】弧长的计算.
【答案】D
【分析】把扇形的圆心角为和半径为代入弧长公式计算即可.
【解答】解:依题意,n=60,r=12,
∴扇形的弧长4π.
故选:D.
【点评】本题考查了弧长公式的运用.关键是熟悉公式:扇形的弧长.
3.(2024秋 南川区期末)如图,在Rt△ABC中,∠C=90°,AB=4,BC=2.以点C为圆心,CB长为半径画弧,分别交AB,AC于点E,D,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;勾股定理.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】连接CE,作EF⊥BC于点F,根据题意得出,CB=CE,得到∠B=60°,可得△BCE是等边三角形,计算S阴=S扇BCE﹣S△BCE即可得到答案.
【解答】解:如图,连接CE,作EF⊥BC于点F,
由条件可知,
∴∠B=60°,
∵CB=CE,
∴△BCE是等边三角形,
∴BE=BC=2,
∴,
∴,
∴,
∴,
故选:C.
【点评】本题考查了扇形面积公式及计算,锐角三角函数,等边三角形的判定和性质,熟练掌握相关知识点是解题的关键.
4.(2024秋 普陀区期末)如图,将△ABC绕点B逆时针旋转n°后得到△A1BC1,其中点A、C分别与点A1、C1对应,AC与A1B交于点O,那么下列说法中错误的是( )
A.AB=A1B
B.∠ABA1=∠CBC1
C.阴影部分的面积与△ABA1的面积相等
D.△AA1O与△BCO的面积相等
【考点】扇形面积的计算;旋转的性质;三角形的面积.
【专题】三角形;平移、旋转与对称;推理能力.
【答案】D
【分析】AB.根据旋转的性质判断即可;
C.设△A1BC1中阴影部分的面积为S1,由S△AOB+S△BOC=S△BOC+S1,得S△AOB=S1,从而得S阴影S1S△AOB;
D.S△AOB,S△BCO+S△AOB=S△ABC,由于S△ABC不一定成立,故S△BCO不一定成立.
【解答】解:根据旋转的性质,AB=A1B,∠ABA1=∠CBC1=n°,
∴AB正确,不符合题意;
设△A1BC1中阴影部分的面积为S1,
∵S△AOB+S△BOC=S△BOC+S1,
∴S△AOB=S1,
∴S阴影S1S△AOB,
∴C正确,不符合题意;
S△AOB,S△BCO+S△AOB=S△ABC,
∵S△ABC不一定成立,
∴S△BCO不一定成立,
∴D错误,符合题意.
故选:D.
【点评】本题考查三角形的面积、旋转的性质,掌握旋转的性质是解题的关键.
5.(2024秋 廉江市期末)如图,在△ABC中,∠ACB=90°,BC=1,AC,将△ABC绕着点A逆时针旋转90°得到△ADE,则图中阴影部分的面积是( )
A. B. C. D.
【考点】扇形面积的计算;旋转的性质;勾股定理.
【专题】平移、旋转与对称;与圆有关的计算;运算能力.
【答案】C
【分析】先利用勾股定理求出AB的长,再根据S阴影=S扇形BAD+S△ADE﹣S扇形ACE﹣S△ABC进行求解即可.
【解答】解:由勾股定理得:,
由旋转的性质可得S△ADE=S△ABC,∠BAD=∠CAE=90°,
∴S阴影=S扇形BAD+S△ADE﹣S扇形CAE﹣S△ABC
=S扇形BAD﹣S扇形CAE
,
故选:C.
【点评】本题主要考查了扇形面积计算,勾股定理,熟练掌握以上知识点是解题的关键.
二.填空题(共5小题)
6.(2024秋 包河区校级期末)如图,扇形的圆心角为120°,点C在圆弧上,∠ABC=30°,OA=2,阴影部分的面积为 .
【考点】扇形面积的计算;圆周角定理.
【专题】运算能力.
【答案】.
【分析】连接OC,AC,由∠ABC的度数得出∠AOC的度数,再将阴影部分的面积转化为扇形OAC的面积,最后根据扇形的面积公式即可解决问题.
【解答】解:连接OA,OC,
∵∠ABC=30°,
∴∠AOC=2×30°=60°.
又∵OA=OC,
∴∠OAC=∠OCA=60°.
∵∠AOB=120°,
∴∠COB=120°﹣60°=60°,
∴∠ACO=∠COB,
∴AC∥OB,
∴S△AOC=S△ABC,
∴S阴影=S扇形OAC.
∵OA=2,
∴,
∴.
故答案为:.
【点评】本题主要考查了扇形面积的计算及圆周角定理,熟知圆周角定理及扇形的面积公式是解题的关键.
7.(2024秋 扬州期末)如图,半径为5的扇形AOB中,∠AOB=90°,点C在OB上,点E在OA上,点D在弧AB上,四边形OCDE是正方形,则图中阴影部分的面积为 .
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD,交CE于点F.由正方形的性质得出S△OEF=S△FCD,∠EOD=45°.即根据扇形面积公式求出扇形AOD的面积即可.
【解答】解:如图,连接OD,交CE于点F.
∵四边形OCDE是正方形,
∴S△OEF=S△FCD,∠EOD=45°,
∴S阴=S扇形AOD.
故答案为:.
【点评】本题考查正方形的性质,扇形的面积公式.理解S阴=S扇形AOD是解题关键.
8.(2024秋 汕尾期末)如图,点C,D是以AB为直径的半圆上的点,且∠COD=60°,半径AO=3,则阴影部分的面积为 .(结果保留π)
【考点】扇形面积的计算.
【专题】运算能力.
【答案】.
【分析】直接运用扇形面积公式求解即可.
【解答】解:根据扇形的面积公式得阴影部分的面积为:.
故答案为:.
【点评】本题主要考查求扇形的面积,掌握扇形的面积公式是解题的关键.
9.(2024秋 合川区期末)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=4,则阴影部分的面积为 .(结果保留π)
【考点】扇形面积的计算;旋转的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD交AB于E,先证明△OAD是等边三角形,∠AOD=∠BOD=60°,从而得到OD⊥AB,AB=2AE,继而求得,,即可由S阴影=S扇形BAC﹣S△ABD,求解.
【解答】解:连接OD交AB于E,
∵∠AOB=120°,OA=OB,
∴∠ABO=∠BAO=∠BAC=30°,
∴∠OAD=60°,
∵OA=OD,
∴∠AOD=60°,AD=OA=4,
∴∠BOD=∠AOB﹣∠AOD=60°,
∴∠BOD=∠AOD,
∴OD⊥AB,AB=2AE,
∴,
∴,
∴,
∴.
故答案为:.
【点评】本题考查了扇形的面积,等边三角形的性质和判定,直角三角形的性质,勾股定理等知识点,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.
10.(2024秋 番禺区期末)如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形.若AB=2,则此莱洛三角形的周长为 2π .
【考点】弧长的计算;等边三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】2π.
【分析】利用弧长计算公式计算即可.
【解答】解:,
∴C=3l=2π,
故答案为:2π.
【点评】本题考查了弧长的计算,等边三角形的性质,掌握弧长的计算公式是解题的关键.
三.解答题(共5小题)
11.(2024秋 盐城期末)如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC,AC分别相交于点D,E.
(1)求证:BD=CD;
(2)若⊙O半径为5,∠CDE=50°,求扇形ODB的面积.
【考点】扇形面积的计算;等腰三角形的性质;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;推理能力.
【答案】(1)见解析;
(2).
【分析】(1)连接AD,根据圆周角定理的推论得到∠BDA=90°,再根据等腰三角形的性质即可得到BD=CD;
(2)根据已知求出∠BOD=50°,根据扇形面积公式即可得到答案.
【解答】(1)证明:连接AD,
∵AB为⊙O的直径,
∴∠BDA=90°,
∴AD⊥BC.
∵AB=AC.
∴BD=CD;
(2)解:∵∠CDE=50°,
∴∠BAC=50°,
∵AD⊥BC.AB=AC.
∴∠BAD=∠CAD=25°,
∴∠BOD=2∠BAD=50°,
∵⊙O半径为5,
∴S扇形ODB.
【点评】本题考查了扇形面积和等腰三角形的性质以及圆周角定理.掌握扇形的面积公式、等腰三角形的性质以及圆周角定理是解题的关键.
12.(2024秋 江都区期末)汽车盲区是造成交通事故的罪魁祸首之一,它是指驾驶员位于正常驾驶座位置,其视线被车体遮挡而不能直接观察到的那部分区域.如图1,有一种汽车盲区叫做内轮差盲区,内轮差是车辆在转弯时前内轮转弯半径与后内轮转弯半径之差,由于内轮差的存在,汽车在转弯时都会产生这种盲区.为了安全,许多路口都设置“右转危险区”标线.图2是货车在路口“右转危险区”的示意图,后内轮转弯半径O1A=O1D=4米,前内轮转弯半径O2B=O2C=a米,∠DO1A=∠CO2B=90°.
(1)图2中O1A,O1D,弧AD围成的扇形面积为 4π平方米 (结果保留π);
(2)用a的代数式表示“右转危险区”的面积,并求出当a=2时,“右转危险区”的面积(结果保留π);
(3)小明站在线段O1O2的延长线上,且与O2的距离为1.2米的地方,若O1、O2之间的距离为3米,请判断小明是否有危险,并说明理由.
【考点】扇形面积的计算;圆周角定理.
【专题】与圆有关的计算;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)4π平方米;
(2)S危险区域=(16﹣4π﹣a2πa2)平方米,
当a=2时,S危险区域=(12﹣3π)平方米;
(3)有危险.
【分析】(1)根据扇形面积的计算公式进行计算即可;
(2)根据正方形面积,扇形面积的计算方法以及图形中各个部分面积之间的关系进行计算即可;
(3)根据图形的对称性,求出小正方形的边长,即小扇形的半径,再根据小扇形半径与1.2的大小关系进行判断即可.
【解答】解:(1)图中O1A,O1D,弧AD围成的扇形面积为4π(平方米),
故答案为:4π平方米;
(2)图中O2C,O2B,弧BC围成的扇形面积为πa2(平方米),
∴S危险区域=(42﹣4π)﹣(a2πa2)
=(16﹣4π﹣a2πa2)平方米,
当a=2时,S危险区域=16﹣4π﹣4+π=(12﹣3π)平方米,
(3)有危险,理由:
如图,连接O1O2并延长一定过点E,则O2E=43,
∴O2C(43),
∵1.75>1.2,
∴有危险.
【点评】本题考查扇形面积的计算,掌握正方形、扇形面积的计算方法是正确解答的关键.
13.(2024秋 临潼区期末)如图,在四边形ABCD中,已知∠A=90°,分别以点B,C,D为圆心,以1cm长为半径作圆,求阴影部分的面积之和.
【考点】扇形面积的计算;三角形的面积.
【专题】与圆有关的计算;运算能力.
【答案】π.
【分析】阴影部分面积之和等于三个扇形面积之和,利用扇形面积公式求解.
【解答】解:⊙B,⊙C,⊙D半径相同,
∴阴影部分面积之和等于三个扇形面积之和,
∵∠A=90°,
∴∠B+∠C+∠D=360°﹣90°=270°,
∴π.
【点评】本题考查扇形面积的计算,三角形的面积,解题的关键是理解题意,灵活运用所学知识解决问题.
14.(2024秋 拱墅区期末)如图,已知⊙O的半径为2,弦CD⊥直径AB,垂足为点E,点F在上(不与点A,点C重合),连接AF,AC,AD,FC.
(1)求证:AC=AD.
(2)若.
①求∠ACD的度数.
②当FC∥AD时,求的长.
【考点】弧长的计算;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1)见解答;
(2)①
②π.
【分析】(1)根据垂径定理及圆心角定理证明;
(2)①根据圆内接四边形的性质求解;
②根据“平行弦所夹的弧相等”,及弧长公式求解.
【解答】(1)证明:∵弦CD⊥直径AB,
∴A平分,即,
∴AC=AD;
(2)①∵四边形AFCD内接于⊙O,
∴∠AFC+∠ADC=180°①,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC②,
由①②得:∠ADC=67.5°,∠AFC=112.5°,
∴∠ACD=67.5°;
②连接OC,OD,
∵∠ADC=∠ACD=67.5°,
∴∠CAD=180°﹣2×67.5°=45°,
∴∠COD=90°,
∵FC∥AD,
∴,
∵的长为:π,
∴的长为π.
【点评】本题考查了弧长公式及垂径定理,掌握弧长公式和垂径定理是解题的关键.
15.(2024秋 滨海新区期末)如图,OA,OB为⊙O的半径,过点A作OA⊥AP,过点B作OB⊥BP,AP与BP相交于点P,连接OP交⊙O于点C,连接BC,若OA∥BC,OA=1.
(Ⅰ)求证:△OBC为等边三角形;
(Ⅱ)求图中阴影部分的面积(结果保留π).
【考点】扇形面积的计算;等边三角形的判定与性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】(Ⅰ)证明见解答;
(Ⅱ).
【分析】(Ⅰ)根据全等三角形的判定与性质、平行线的性质和等边三角形的判定定理证明即可;
(Ⅱ)利用特殊角的三角形函数和三角形面积公式求出S四边形OAPB,利用扇形面积公式求出S扇形AOB,再由S阴影=S四边形OAPB﹣S扇形AOB计算阴影部分的面积即可.
【解答】(Ⅰ)证明:在Rt△OAP和Rt△OBP中,
,
∴Rt△OAP≌Rt△OBP(HL),
∴∠AOP=∠BOP,
∵OA∥BC,
∴∠BCO=∠AOP,
∴∠BOP=∠BCO,
∵OB=OC,
∴∠OBC=∠BCO,
∴∠OBC=∠BCO=∠BOP,
∴△OBC为等边三角形.
(Ⅱ)∵△OBC为等边三角形,
∴∠BOP=60°,
∴BP=OB tan∠BOP=1,
∴SRt△OBP=SRt△OAPOB BP1,
∴S四边形OAPB=SRt△OBP+SRt△OAP,
∵∠AOB=2∠BOP=120°,
∴S扇形AOBπ×12,
∴S阴影=S四边形OAPB﹣S扇形AOB.
【点评】本题考查扇形面积的计算、等边三角形的判定与性质,掌握扇形面积的计算公式、等边三角形的判定与性质、等三角形的判定与性质、平行线的性质、特殊角的三角形函数和三角形面积公式是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
