【中考押题卷】2025年北师大版中考数学考前冲刺:切线长定理(含解析)
文档属性
| 名称 | 【中考押题卷】2025年北师大版中考数学考前冲刺:切线长定理(含解析) | 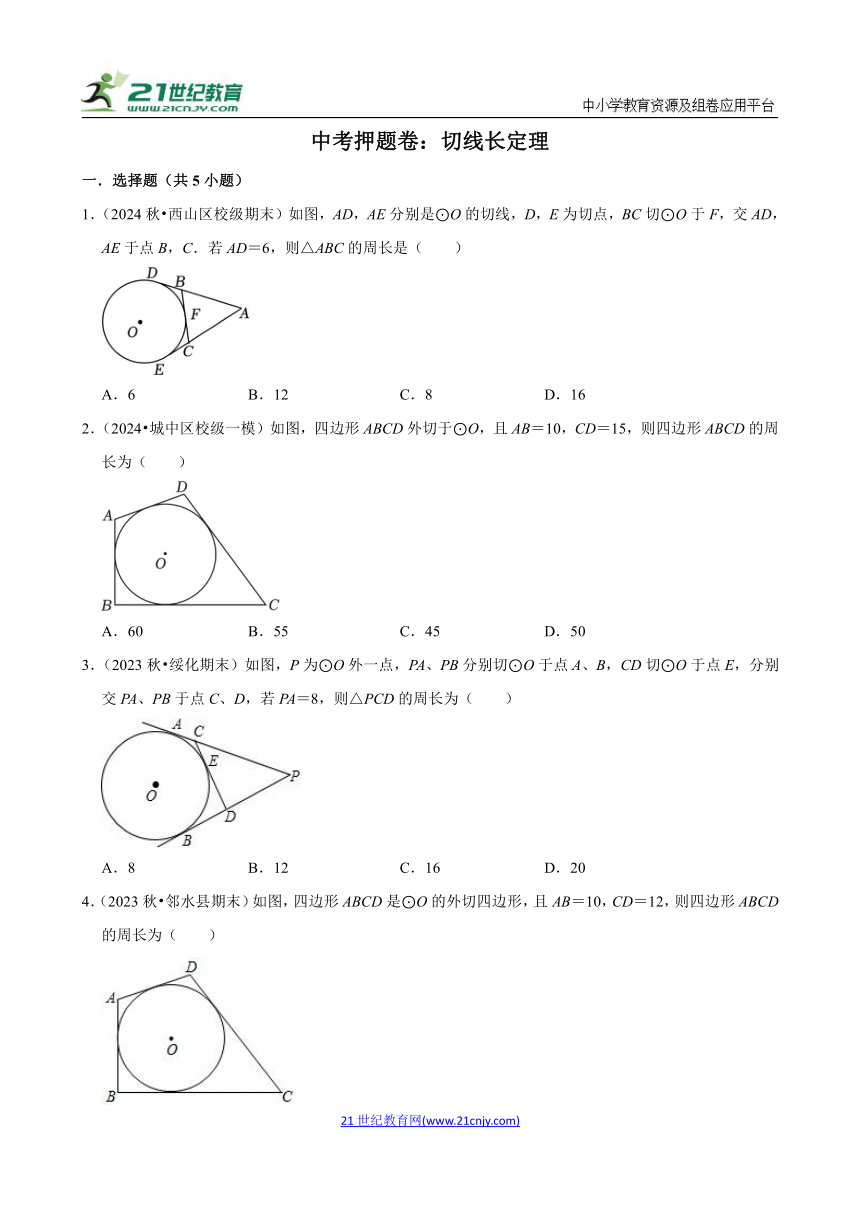 | |
| 格式 | docx | ||
| 文件大小 | 859.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:22:54 | ||
图片预览





文档简介
中考押题卷:切线长定理
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C.若AD=6,则△ABC的周长是( )
A.6 B.12 C.8 D.16
2.(2024 城中区校级一模)如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
3.(2023秋 绥化期末)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
4.(2023秋 邻水县期末)如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
5.(2023秋 鄂伦春自治旗校级月考)如图,PA,PB为⊙O的两条切线,C,D切⊙O于点E,分别交PA,PB于点C,D.F为⊙O上的点,连接AF,BF,若PA=5,∠P=40°,则△PCD的周长和∠AFB的度数分别为( )
A.10,40° B.10,80° C.15,70° D.10,70°
二.填空题(共5小题)
6.(2024秋 林州市期中)如图,一圆内切于四边形ABCD,且AB=10,CD=8,则四边形的周长为 .
7.(2024秋 西城区校级期中)如图,过圆外一点A作⊙O的切线AB,AC,切点分别是B,C,连接BC.过上一点D作⊙O的切线,分别交AB,AC于点E,F.若∠A=90°,△AEF的周长为4,则BC的长为 .
8.(2024 凉州区三模)如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为 cm.
9.(2024秋 大连期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 .
10.(2024秋 莒县期中)如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 .
三.解答题(共5小题)
11.(2024秋 东胜区期中)如图,AB为⊙O的直径,过圆外一点E作⊙O的两条切线EC,EB,切点分别为点D,B,EC交BA的延长线于点C,连接OE,AD.
(1)AD与OE有怎样的位置关系?并说明理由;
(2)若EB=6,CD=4,求⊙O的半径.
12.(2022秋 任城区校级月考)如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
13.(2022 惠水县模拟)如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.
(1)求CD的长度.
(2)求EG的长度.
(3)求FB的长度.
14.(2021秋 高安市期末)如图,PA、PB、CD是⊙O的切线,点A、B、E为切点.
(1)如果△PCD的周长为10,求PA的长;
(2)如果∠P=40°,
①求∠COD;
②连AE,BE,求∠AEB.
15.(2021 滨海县一模)如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
中考押题卷:切线长定理
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C.若AD=6,则△ABC的周长是( )
A.6 B.12 C.8 D.16
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】B
【分析】先利用切线长定理AD=AE,BD=BF,CF=CE,然后利用等线段代换得到△ABC的周长=2AD.
【解答】解:∵AD,AE分别是⊙O的切线,
∴AE=AD,
∵BD、BC分别为⊙O的切线,
∴BD=BF,
∵CF、CE分别为⊙O的切线,
∴CE=CF,
∴三角形ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BD+AC+CE=AD+AE=2AD=12.
故选:B.
【点评】本题考查了切线长的性质:灵活运用切线长定理和等线段代换是解决问题的关键.
2.(2024 城中区校级一模)如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】D
【分析】根据切线长定理得到AE=AF,BE=BG,CG=CH,DH=DF,进而求出AD+BC,再根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD外切于⊙O,切点分别为E、G、H、F,
∴AE=AF,BE=BG,CG=CH,DH=DF,
∴AD+BC=AF+DF+BG+CG=AE+DH+BE+CG=AB+CD=10+15=25,
∴四边形ABCD的周长为:AD+BC+AB+CD=25+25=50,
故选:D.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等.
3.(2023秋 绥化期末)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
【考点】切线长定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】C
【分析】由切线长定理可求得PA=PB,AC=CE,BD=ED,则可求得答案.
【解答】解:∵PA、PB分别切⊙O于点A、B,CD切⊙O于点E,
∴PA=PB=8,AC=EC,BD=ED,
∴PC+CD+PD=PC+CE+DE+PD=PA+AC+PD+BD=PA+PB=8+8=16,
即△PCD的周长为16.
故选:C.
【点评】本题主要考查切线的性质,利用切线长定理求得PA=PB、AC=CE和BD=ED是解题的关键.
4.(2023秋 邻水县期末)如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
【考点】切线长定理.
【专题】与圆有关的计算;推理能力.
【答案】A
【分析】根据圆外切四边形的对边之和相等求出AD+BC,根据四边形的周长公式计算即可.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
【点评】本题考查的是切线长定理,掌握圆外切四边形的对边之和相等是解题的关键.
5.(2023秋 鄂伦春自治旗校级月考)如图,PA,PB为⊙O的两条切线,C,D切⊙O于点E,分别交PA,PB于点C,D.F为⊙O上的点,连接AF,BF,若PA=5,∠P=40°,则△PCD的周长和∠AFB的度数分别为( )
A.10,40° B.10,80° C.15,70° D.10,70°
【考点】切线长定理;圆周角定理;切线的性质.
【专题】与圆有关的计算;几何直观;推理能力.
【答案】D
【分析】连接OA,OB,可得∠OAP=∠OBP=90°,CA=CE,DB=DE,PA=PB;据此即可求解.
【解答】解:连接OA,OB,如图所示:
由切线的性质以及切线长定理得:∠OAP=∠OBP=90°,CA=CE,DB=DE,PA=PB,
∵∠P=40°,
∴∠AOB=360°﹣∠P﹣∠OAP﹣∠OBP=140°,
∴;
△PCD的周长=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=2PA=10,
故选:D.
【点评】本题考查了切线长定理,圆周角定理,切线的性质,解答本题的关键是熟练运用圆周角定理解决问题.
二.填空题(共5小题)
6.(2024秋 林州市期中)如图,一圆内切于四边形ABCD,且AB=10,CD=8,则四边形的周长为 36 .
【考点】切线长定理.
【专题】一次函数及其应用;图形的全等;应用意识.
【答案】36.
【分析】如图,设AB与⊙O相切于点E,BC与⊙O相切于点F,CD与⊙O相切于点G,AD与⊙O相切于点H,根据切线长定理得到AE=AH,BE=BF,CF=CG,DG=DH,进而得到AB+CD=AD+BC=18,由此即可求出四边形的周长.
【解答】解:∵一圆内切于四边形ABCD,且AB=10,CD=8,如图,设AB与⊙O相切于点E,BC与⊙O相切于点F,CD与⊙O相切于点G,AD与⊙O相切于点H,
∴AE=AH,BE=BF,CF=CG,DG=DH,
∴AE+BE+CG+DG=AH+BF+CF+DH,
∴AB+CD=AD+BC,
∴AB+CD+AD+BC=2(AB+CD)=2×(10+8)=36,
即四边形的周长为36,
故答案为:36.
【点评】本题考查了切线长定理,解答本题的关键是熟练掌握全等三角全等.
7.(2024秋 西城区校级期中)如图,过圆外一点A作⊙O的切线AB,AC,切点分别是B,C,连接BC.过上一点D作⊙O的切线,分别交AB,AC于点E,F.若∠A=90°,△AEF的周长为4,则BC的长为 .
【考点】切线长定理;勾股定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力.
【答案】.
【分析】先根据切线长定理得AB=AC,EB=ED,DF=CF,再根据△AEF的周长=AE+AF+EF=AE+DE+AF+DF=AE+BE+AF+CF=AB+AC,可求AB,AC,然后根据勾股定理求出答案.
【解答】解:∵AB,AC,EF是⊙O的切线,
∴AB=AC,EB=ED,DF=CF.
∵△AEF的周长
=AE+AF+EF=AE+DE+AF+DF=AE+BE+AF+CF=AB+AC,
∴AB+AC=4,
∴AB=AC=2.
∵BC2=AB2+AC2,
∴.
故答案为:.
【点评】本题主要考查了切线长定理,勾股定理,掌握切线长定理是解题的关键.
8.(2024 凉州区三模)如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为 20 cm.
【考点】切线长定理.
【专题】计算题.
【答案】见试题解答内容
【分析】利用切线长定理,可以得到:PA=PB,AE=EC,FC=FB,据此即可求解
【解答】解:∵PA,PB是圆的切线.
∴PA=PB
同理,AE=EC,FC=FB.
三角形PEF的周长=PE+EF+PF=PE+PF+CF+EC=PE+AE+PF+FB=PA+PB=2PA=20cm.
故答案是20.
【点评】本题主要考查了切线长定理,对于定理的认识,在图形中找到切线长定理的基本图形是解决本题的关键.
9.(2024秋 大连期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 3 .
【考点】切线长定理.
【专题】计算题;运算能力;推理能力.
【答案】见试题解答内容
【分析】由AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【解答】解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=8﹣5=3.
故答案为:3.
【点评】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
10.(2024秋 莒县期中)如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 14 .
【考点】切线长定理;正方形的性质.
【答案】见试题解答内容
【分析】根据切线的性质知:AE=EF,BC=CF;根据△CDE的周长可求出正方形ABCD的边长;在Rt△CDE中,利用勾股定理可将AE的长求出,进而可求出直角梯形ABCE的周长.
【解答】解:设AE的长为x,正方形ABCD的边长为a,
∵CE与半圆O相切于点F,
∴AE=EF,BC=CF,
∵EF+FC+CD+ED=12,
∴AE+ED+CD+BC=12,
∵AD=CD=BC=AB,
∴正方形ABCD的边长为4;
在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,
∴AE+EF+FC+BC+AB=14,
∴直角梯形ABCE周长为14.
故答案为:14.
【点评】本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
三.解答题(共5小题)
11.(2024秋 东胜区期中)如图,AB为⊙O的直径,过圆外一点E作⊙O的两条切线EC,EB,切点分别为点D,B,EC交BA的延长线于点C,连接OE,AD.
(1)AD与OE有怎样的位置关系?并说明理由;
(2)若EB=6,CD=4,求⊙O的半径.
【考点】切线长定理;平行线的判定;全等三角形的判定与性质;等腰三角形的性质;勾股定理.
【专题】图形的全等;等腰三角形与直角三角形;与圆有关的位置关系;运算能力;推理能力.
【答案】(1)AD∥OE,理由见解析;
(2)3.
【分析】(1)连接OD,根据切线的定义可得∠ODE=∠OBE=90°,再证明Rt△DOE≌Rt△BOE(HL),再由等腰三角形性质可得∠ODA=∠OAD,最后由平行线的判定证明即可;
(2)根据切线长定理先求得ED长,再根据勾股定理求得BC长,再设OB=OD=r,则OC=8﹣r,利用勾股定理解求解即可.
【解答】解:(1)AD∥OE,
理由:∵CE,BE是⊙O的切线,
∴∠ODE=∠OBE=90°,
在Rt△DOE和Rt△BOE中,
,
∴Rt△DOE≌Rt△BOE(HL),
∴∠DOE=∠BOE,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠DOB=∠DOE+∠BOE=∠ODA+∠OAD,
∵∠DOE=∠ODA,
∴AD∥OE;
(2)∵CE,BE是⊙O的切线,
∴DE=BE=6,
∴CE=DE+CE=6+4=10,
∴BC8,
设OB=OD=r,则OC=8﹣r,
∵CD2+OD2=OC2,
∴42+r2=(8﹣r)2,
解得r=3,
即⊙O半径的长为3.
【点评】本题考查切线的性质,切线长定理,全等三角形的性质和判定,勾股定理,平行线的判定等:掌握切线的性质,切线长定理是解题的关键.
12.(2022秋 任城区校级月考)如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
【考点】切线长定理.
【答案】见试题解答内容
【分析】设⊙O切AB于M,切BC于N,连接OM、ON,求出四边形BMON是正方形,求出BM=BN=3,根据切线长定理求出EM=EP,FP=FN,最后求出△BEF的周长=BM+BN,代入求出即可.
【解答】解:设⊙O切AB于M,切BC于N,连接OM、ON,
则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ONAB6=3,
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
【点评】本题考查了切线长定理,正方形的性质和判定,正方形的内切圆的应用,解此题的关键是求出△BEF的周长=BN+BM和求出BM的长,注意:从圆外一点引圆的两条切线,它们的切线长相等.
13.(2022 惠水县模拟)如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.
(1)求CD的长度.
(2)求EG的长度.
(3)求FB的长度.
【考点】切线长定理;圆周角定理;切线的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)8;
(2);
(3)3.
【分析】(1)根据切线的判定定理得到DA、CB都是圆O的切线,根据求写出定理分别求出DE、CE,进而求出CD;
(2)证明△DEG∽△DCB,根据相似三角形的性质求出EG;
(3)证明AD∥EG∥BC,根据平行线分线段成比例定理列出比例式,计算即可.
【解答】解:(1)∵AB为圆O直径,∠DAB=∠ABC=90°,
∴DA、CB都是圆O的切线,
∵CD与圆O相切于点E,
∴DE=DA=2,CE=CB=6,
∴CD=DE+CE=8;
(2)∵∠ABC=90°,EF⊥AB,
∴EG∥BC,
∴△DEG∽△DCB,
∴,即,
解得:EG;
(3)过点D作DH⊥BC于H,
则四边形DABH为矩形,
∴BH=AD=2,
∴CH=BC﹣BH=4,
∴DH4,
∴AB=DH=4,
∵∠DAB=∠ABC=90°,EF⊥AB,
∴AD∥EG∥BC,
∴,即,
解得:BF=3.
【点评】本题考查的是切线长定理、相似三角形的判定和性质、平行线分线段成比例定理的应用,灵活运用切线长定理是解题的关键.
14.(2021秋 高安市期末)如图,PA、PB、CD是⊙O的切线,点A、B、E为切点.
(1)如果△PCD的周长为10,求PA的长;
(2)如果∠P=40°,
①求∠COD;
②连AE,BE,求∠AEB.
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)5;
(2)①70°;
②110°.
【分析】(1)根据切线长定理和三角形的周长可解答;
(2)①先根据三角形内角和定理可得∠PCD+∠PDC=140°,由平角的定义得∠ACD+∠BDE=220°,由切线长定理:圆外一点与圆心的连线平分切线所成的夹角可得∠ACO=∠DCO∠ACD,∠BDO=∠EDO∠BDE,从而可以解答;
②根据平角的定义和三角形的内角和定理可解答.
【解答】解:(1)∵PA、PB、CD是⊙O的切线,点A、B、E为切点,
∴PA=PB,AC=CE,ED=BD,
∵△PCD的周长为10,
∴PC+CD+PD=10,
∴PC+CE+DE+PD=PC+AC+PD+BD=PA+PB=2PA=10,
∴PA=5;
(2)①∵∠P=40°,
∴∠PCD+∠PDC=180°﹣40°=140°,
∴∠ACD+∠BDE=360°﹣140°=220°,
∵PA、PB、CD是⊙O的切线,点A、B、E为切点,
∴∠ACO=∠DCO∠ACD,∠BDO=∠EDO∠BDE,
∴∠OCD+∠ODC220°=110°,
∴∠COD=180°﹣110°=70°;
②∠AEB=180°﹣∠AEC﹣∠BED
=180°
=180°﹣90°∠ACD﹣90°∠BDE
220°
=110°.
【点评】本题考查的是切线长定理,三角形内角和定理,掌握切线长定理是解题的关键.
15.(2021 滨海县一模)如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
【考点】切线长定理.
【答案】见试题解答内容
【分析】(1)可通过切线长定理将相等的线段进行转换,得出三角形PCD的周长等于PA+PB的结论,即可求出PA的长;
(2)根据三角形的内角和求出∠ACD和∠BDC的度数和,然后根据切线长定理,得出∠DCO和∠ODE的度数和,再根据三角形的内角和求出∠COD的度数.
【解答】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA∠ACD;
同理:∠ODE∠CDB,
∴∠OCE+∠ODE(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
【点评】本题考查的是切线长定理,切线长定理提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C.若AD=6,则△ABC的周长是( )
A.6 B.12 C.8 D.16
2.(2024 城中区校级一模)如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
3.(2023秋 绥化期末)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
4.(2023秋 邻水县期末)如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
5.(2023秋 鄂伦春自治旗校级月考)如图,PA,PB为⊙O的两条切线,C,D切⊙O于点E,分别交PA,PB于点C,D.F为⊙O上的点,连接AF,BF,若PA=5,∠P=40°,则△PCD的周长和∠AFB的度数分别为( )
A.10,40° B.10,80° C.15,70° D.10,70°
二.填空题(共5小题)
6.(2024秋 林州市期中)如图,一圆内切于四边形ABCD,且AB=10,CD=8,则四边形的周长为 .
7.(2024秋 西城区校级期中)如图,过圆外一点A作⊙O的切线AB,AC,切点分别是B,C,连接BC.过上一点D作⊙O的切线,分别交AB,AC于点E,F.若∠A=90°,△AEF的周长为4,则BC的长为 .
8.(2024 凉州区三模)如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为 cm.
9.(2024秋 大连期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 .
10.(2024秋 莒县期中)如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 .
三.解答题(共5小题)
11.(2024秋 东胜区期中)如图,AB为⊙O的直径,过圆外一点E作⊙O的两条切线EC,EB,切点分别为点D,B,EC交BA的延长线于点C,连接OE,AD.
(1)AD与OE有怎样的位置关系?并说明理由;
(2)若EB=6,CD=4,求⊙O的半径.
12.(2022秋 任城区校级月考)如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
13.(2022 惠水县模拟)如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.
(1)求CD的长度.
(2)求EG的长度.
(3)求FB的长度.
14.(2021秋 高安市期末)如图,PA、PB、CD是⊙O的切线,点A、B、E为切点.
(1)如果△PCD的周长为10,求PA的长;
(2)如果∠P=40°,
①求∠COD;
②连AE,BE,求∠AEB.
15.(2021 滨海县一模)如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
中考押题卷:切线长定理
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C.若AD=6,则△ABC的周长是( )
A.6 B.12 C.8 D.16
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】B
【分析】先利用切线长定理AD=AE,BD=BF,CF=CE,然后利用等线段代换得到△ABC的周长=2AD.
【解答】解:∵AD,AE分别是⊙O的切线,
∴AE=AD,
∵BD、BC分别为⊙O的切线,
∴BD=BF,
∵CF、CE分别为⊙O的切线,
∴CE=CF,
∴三角形ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BD+AC+CE=AD+AE=2AD=12.
故选:B.
【点评】本题考查了切线长的性质:灵活运用切线长定理和等线段代换是解决问题的关键.
2.(2024 城中区校级一模)如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】D
【分析】根据切线长定理得到AE=AF,BE=BG,CG=CH,DH=DF,进而求出AD+BC,再根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD外切于⊙O,切点分别为E、G、H、F,
∴AE=AF,BE=BG,CG=CH,DH=DF,
∴AD+BC=AF+DF+BG+CG=AE+DH+BE+CG=AB+CD=10+15=25,
∴四边形ABCD的周长为:AD+BC+AB+CD=25+25=50,
故选:D.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等.
3.(2023秋 绥化期末)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
【考点】切线长定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】C
【分析】由切线长定理可求得PA=PB,AC=CE,BD=ED,则可求得答案.
【解答】解:∵PA、PB分别切⊙O于点A、B,CD切⊙O于点E,
∴PA=PB=8,AC=EC,BD=ED,
∴PC+CD+PD=PC+CE+DE+PD=PA+AC+PD+BD=PA+PB=8+8=16,
即△PCD的周长为16.
故选:C.
【点评】本题主要考查切线的性质,利用切线长定理求得PA=PB、AC=CE和BD=ED是解题的关键.
4.(2023秋 邻水县期末)如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
【考点】切线长定理.
【专题】与圆有关的计算;推理能力.
【答案】A
【分析】根据圆外切四边形的对边之和相等求出AD+BC,根据四边形的周长公式计算即可.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故选:A.
【点评】本题考查的是切线长定理,掌握圆外切四边形的对边之和相等是解题的关键.
5.(2023秋 鄂伦春自治旗校级月考)如图,PA,PB为⊙O的两条切线,C,D切⊙O于点E,分别交PA,PB于点C,D.F为⊙O上的点,连接AF,BF,若PA=5,∠P=40°,则△PCD的周长和∠AFB的度数分别为( )
A.10,40° B.10,80° C.15,70° D.10,70°
【考点】切线长定理;圆周角定理;切线的性质.
【专题】与圆有关的计算;几何直观;推理能力.
【答案】D
【分析】连接OA,OB,可得∠OAP=∠OBP=90°,CA=CE,DB=DE,PA=PB;据此即可求解.
【解答】解:连接OA,OB,如图所示:
由切线的性质以及切线长定理得:∠OAP=∠OBP=90°,CA=CE,DB=DE,PA=PB,
∵∠P=40°,
∴∠AOB=360°﹣∠P﹣∠OAP﹣∠OBP=140°,
∴;
△PCD的周长=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=2PA=10,
故选:D.
【点评】本题考查了切线长定理,圆周角定理,切线的性质,解答本题的关键是熟练运用圆周角定理解决问题.
二.填空题(共5小题)
6.(2024秋 林州市期中)如图,一圆内切于四边形ABCD,且AB=10,CD=8,则四边形的周长为 36 .
【考点】切线长定理.
【专题】一次函数及其应用;图形的全等;应用意识.
【答案】36.
【分析】如图,设AB与⊙O相切于点E,BC与⊙O相切于点F,CD与⊙O相切于点G,AD与⊙O相切于点H,根据切线长定理得到AE=AH,BE=BF,CF=CG,DG=DH,进而得到AB+CD=AD+BC=18,由此即可求出四边形的周长.
【解答】解:∵一圆内切于四边形ABCD,且AB=10,CD=8,如图,设AB与⊙O相切于点E,BC与⊙O相切于点F,CD与⊙O相切于点G,AD与⊙O相切于点H,
∴AE=AH,BE=BF,CF=CG,DG=DH,
∴AE+BE+CG+DG=AH+BF+CF+DH,
∴AB+CD=AD+BC,
∴AB+CD+AD+BC=2(AB+CD)=2×(10+8)=36,
即四边形的周长为36,
故答案为:36.
【点评】本题考查了切线长定理,解答本题的关键是熟练掌握全等三角全等.
7.(2024秋 西城区校级期中)如图,过圆外一点A作⊙O的切线AB,AC,切点分别是B,C,连接BC.过上一点D作⊙O的切线,分别交AB,AC于点E,F.若∠A=90°,△AEF的周长为4,则BC的长为 .
【考点】切线长定理;勾股定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力.
【答案】.
【分析】先根据切线长定理得AB=AC,EB=ED,DF=CF,再根据△AEF的周长=AE+AF+EF=AE+DE+AF+DF=AE+BE+AF+CF=AB+AC,可求AB,AC,然后根据勾股定理求出答案.
【解答】解:∵AB,AC,EF是⊙O的切线,
∴AB=AC,EB=ED,DF=CF.
∵△AEF的周长
=AE+AF+EF=AE+DE+AF+DF=AE+BE+AF+CF=AB+AC,
∴AB+AC=4,
∴AB=AC=2.
∵BC2=AB2+AC2,
∴.
故答案为:.
【点评】本题主要考查了切线长定理,勾股定理,掌握切线长定理是解题的关键.
8.(2024 凉州区三模)如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为 20 cm.
【考点】切线长定理.
【专题】计算题.
【答案】见试题解答内容
【分析】利用切线长定理,可以得到:PA=PB,AE=EC,FC=FB,据此即可求解
【解答】解:∵PA,PB是圆的切线.
∴PA=PB
同理,AE=EC,FC=FB.
三角形PEF的周长=PE+EF+PF=PE+PF+CF+EC=PE+AE+PF+FB=PA+PB=2PA=20cm.
故答案是20.
【点评】本题主要考查了切线长定理,对于定理的认识,在图形中找到切线长定理的基本图形是解决本题的关键.
9.(2024秋 大连期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 3 .
【考点】切线长定理.
【专题】计算题;运算能力;推理能力.
【答案】见试题解答内容
【分析】由AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【解答】解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=8﹣5=3.
故答案为:3.
【点评】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
10.(2024秋 莒县期中)如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 14 .
【考点】切线长定理;正方形的性质.
【答案】见试题解答内容
【分析】根据切线的性质知:AE=EF,BC=CF;根据△CDE的周长可求出正方形ABCD的边长;在Rt△CDE中,利用勾股定理可将AE的长求出,进而可求出直角梯形ABCE的周长.
【解答】解:设AE的长为x,正方形ABCD的边长为a,
∵CE与半圆O相切于点F,
∴AE=EF,BC=CF,
∵EF+FC+CD+ED=12,
∴AE+ED+CD+BC=12,
∵AD=CD=BC=AB,
∴正方形ABCD的边长为4;
在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,
∴AE+EF+FC+BC+AB=14,
∴直角梯形ABCE周长为14.
故答案为:14.
【点评】本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
三.解答题(共5小题)
11.(2024秋 东胜区期中)如图,AB为⊙O的直径,过圆外一点E作⊙O的两条切线EC,EB,切点分别为点D,B,EC交BA的延长线于点C,连接OE,AD.
(1)AD与OE有怎样的位置关系?并说明理由;
(2)若EB=6,CD=4,求⊙O的半径.
【考点】切线长定理;平行线的判定;全等三角形的判定与性质;等腰三角形的性质;勾股定理.
【专题】图形的全等;等腰三角形与直角三角形;与圆有关的位置关系;运算能力;推理能力.
【答案】(1)AD∥OE,理由见解析;
(2)3.
【分析】(1)连接OD,根据切线的定义可得∠ODE=∠OBE=90°,再证明Rt△DOE≌Rt△BOE(HL),再由等腰三角形性质可得∠ODA=∠OAD,最后由平行线的判定证明即可;
(2)根据切线长定理先求得ED长,再根据勾股定理求得BC长,再设OB=OD=r,则OC=8﹣r,利用勾股定理解求解即可.
【解答】解:(1)AD∥OE,
理由:∵CE,BE是⊙O的切线,
∴∠ODE=∠OBE=90°,
在Rt△DOE和Rt△BOE中,
,
∴Rt△DOE≌Rt△BOE(HL),
∴∠DOE=∠BOE,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠DOB=∠DOE+∠BOE=∠ODA+∠OAD,
∵∠DOE=∠ODA,
∴AD∥OE;
(2)∵CE,BE是⊙O的切线,
∴DE=BE=6,
∴CE=DE+CE=6+4=10,
∴BC8,
设OB=OD=r,则OC=8﹣r,
∵CD2+OD2=OC2,
∴42+r2=(8﹣r)2,
解得r=3,
即⊙O半径的长为3.
【点评】本题考查切线的性质,切线长定理,全等三角形的性质和判定,勾股定理,平行线的判定等:掌握切线的性质,切线长定理是解题的关键.
12.(2022秋 任城区校级月考)如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
【考点】切线长定理.
【答案】见试题解答内容
【分析】设⊙O切AB于M,切BC于N,连接OM、ON,求出四边形BMON是正方形,求出BM=BN=3,根据切线长定理求出EM=EP,FP=FN,最后求出△BEF的周长=BM+BN,代入求出即可.
【解答】解:设⊙O切AB于M,切BC于N,连接OM、ON,
则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ONAB6=3,
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
【点评】本题考查了切线长定理,正方形的性质和判定,正方形的内切圆的应用,解此题的关键是求出△BEF的周长=BN+BM和求出BM的长,注意:从圆外一点引圆的两条切线,它们的切线长相等.
13.(2022 惠水县模拟)如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.
(1)求CD的长度.
(2)求EG的长度.
(3)求FB的长度.
【考点】切线长定理;圆周角定理;切线的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)8;
(2);
(3)3.
【分析】(1)根据切线的判定定理得到DA、CB都是圆O的切线,根据求写出定理分别求出DE、CE,进而求出CD;
(2)证明△DEG∽△DCB,根据相似三角形的性质求出EG;
(3)证明AD∥EG∥BC,根据平行线分线段成比例定理列出比例式,计算即可.
【解答】解:(1)∵AB为圆O直径,∠DAB=∠ABC=90°,
∴DA、CB都是圆O的切线,
∵CD与圆O相切于点E,
∴DE=DA=2,CE=CB=6,
∴CD=DE+CE=8;
(2)∵∠ABC=90°,EF⊥AB,
∴EG∥BC,
∴△DEG∽△DCB,
∴,即,
解得:EG;
(3)过点D作DH⊥BC于H,
则四边形DABH为矩形,
∴BH=AD=2,
∴CH=BC﹣BH=4,
∴DH4,
∴AB=DH=4,
∵∠DAB=∠ABC=90°,EF⊥AB,
∴AD∥EG∥BC,
∴,即,
解得:BF=3.
【点评】本题考查的是切线长定理、相似三角形的判定和性质、平行线分线段成比例定理的应用,灵活运用切线长定理是解题的关键.
14.(2021秋 高安市期末)如图,PA、PB、CD是⊙O的切线,点A、B、E为切点.
(1)如果△PCD的周长为10,求PA的长;
(2)如果∠P=40°,
①求∠COD;
②连AE,BE,求∠AEB.
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)5;
(2)①70°;
②110°.
【分析】(1)根据切线长定理和三角形的周长可解答;
(2)①先根据三角形内角和定理可得∠PCD+∠PDC=140°,由平角的定义得∠ACD+∠BDE=220°,由切线长定理:圆外一点与圆心的连线平分切线所成的夹角可得∠ACO=∠DCO∠ACD,∠BDO=∠EDO∠BDE,从而可以解答;
②根据平角的定义和三角形的内角和定理可解答.
【解答】解:(1)∵PA、PB、CD是⊙O的切线,点A、B、E为切点,
∴PA=PB,AC=CE,ED=BD,
∵△PCD的周长为10,
∴PC+CD+PD=10,
∴PC+CE+DE+PD=PC+AC+PD+BD=PA+PB=2PA=10,
∴PA=5;
(2)①∵∠P=40°,
∴∠PCD+∠PDC=180°﹣40°=140°,
∴∠ACD+∠BDE=360°﹣140°=220°,
∵PA、PB、CD是⊙O的切线,点A、B、E为切点,
∴∠ACO=∠DCO∠ACD,∠BDO=∠EDO∠BDE,
∴∠OCD+∠ODC220°=110°,
∴∠COD=180°﹣110°=70°;
②∠AEB=180°﹣∠AEC﹣∠BED
=180°
=180°﹣90°∠ACD﹣90°∠BDE
220°
=110°.
【点评】本题考查的是切线长定理,三角形内角和定理,掌握切线长定理是解题的关键.
15.(2021 滨海县一模)如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
【考点】切线长定理.
【答案】见试题解答内容
【分析】(1)可通过切线长定理将相等的线段进行转换,得出三角形PCD的周长等于PA+PB的结论,即可求出PA的长;
(2)根据三角形的内角和求出∠ACD和∠BDC的度数和,然后根据切线长定理,得出∠DCO和∠ODE的度数和,再根据三角形的内角和求出∠COD的度数.
【解答】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA∠ACD;
同理:∠ODE∠CDB,
∴∠OCE+∠ODE(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
【点评】本题考查的是切线长定理,切线长定理提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
21世纪教育网(www.21cnjy.com)
同课章节目录
