【中考押题卷】2025年北师大版中考数学考前冲刺:锐角三角函数(含解析)
文档属性
| 名称 | 【中考押题卷】2025年北师大版中考数学考前冲刺:锐角三角函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 392.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览




文档简介
中考押题卷:锐角三角函数
一.选择题(共5小题)
1.(2024秋 金东区期末)在Rt△ABC中,∠C=90°,AB=2,AC=1,则sinA的值为( )
A. B. C. D.
2.(2024秋 泉港区期末)如图,在Rt△ABC中,∠C=90°,下列结论中正确的是( )
A. B. C. D.
3.(2025 崇明区一模)在锐角△ABC中,如果各边长都缩小为原来的,那么∠A的正弦值( )
A.扩大为原来的2倍 B.缩小为原来的
C.大小不变 D.不能确定
4.(2024秋 莱芜区期末)如图,在Rt△ABC中,∠B=90°,若,AB=BD,则sinC=( )
A. B. C. D.
5.(2024秋 丽水期末)在Rt△ABC中,∠C=90°,AC=12,BC=5,则tanA的值是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 梁溪区校级期末)如图,△ABC中,∠C=90°,AC=4,BC=3,则sinA的值为 .
7.(2024秋 市北区期末)在△ABC中,∠C=90°,AC=6,,则BC= .
8.(2024秋 嵊州市期末)在Rt△ABC中,∠ACB=90°,AC=3,AB=5,则sin∠B的值是 .
9.(2025 闵行区一模)在Rt△ABC中,∠C=90°,AB=10,cosA,那么直角边AC长为 .
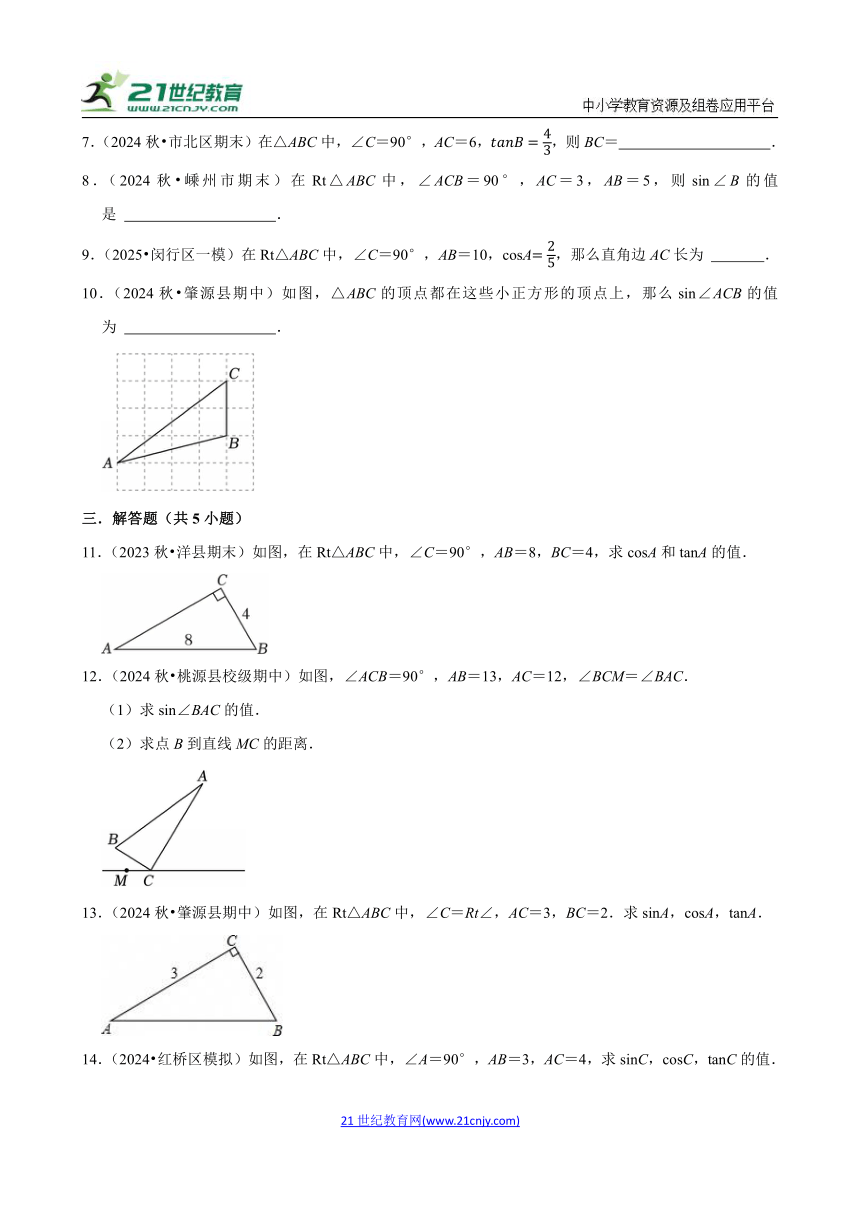
10.(2024秋 肇源县期中)如图,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
三.解答题(共5小题)
11.(2023秋 洋县期末)如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cosA和tanA的值.
12.(2024秋 桃源县校级期中)如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC.
(1)求sin∠BAC的值.
(2)求点B到直线MC的距离.
13.(2024秋 肇源县期中)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
14.(2024 红桥区模拟)如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sinC,cosC,tanC的值.
15.(2024 秦都区校级一模)在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b,求∠B;
(2)已知c=12,sinA,求b.
中考押题卷:锐角三角函数
参考答案与试题解析
题号 1 2 3 4 5
答案 D D C B A
一.选择题(共5小题)
1.(2024秋 金东区期末)在Rt△ABC中,∠C=90°,AB=2,AC=1,则sinA的值为( )
A. B. C. D.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】先根据勾股定理计算出BC,然后利用正弦的定义求解即可.
【解答】解:∵∠C=90°,AB=2,AC=1,
∴BC,
∴sinA.
故选:D.
【点评】本题考查了锐角三角函数的定义和勾股定理,牢记锐角三角函数的定义是解题的关键.
2.(2024秋 泉港区期末)如图,在Rt△ABC中,∠C=90°,下列结论中正确的是( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】根据正切与余弦的定义,即可解答.
【解答】解:在Rt△ABC中,∠C=90°,cosA,tanA,
故选:D.
【点评】本题考查了锐角三角函数的定义,熟练掌握正切与余弦的定义是解题的关键.
3.(2025 崇明区一模)在锐角△ABC中,如果各边长都缩小为原来的,那么∠A的正弦值( )
A.扩大为原来的2倍 B.缩小为原来的
C.大小不变 D.不能确定
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;推理能力.
【答案】C
【分析】锐角三角函数值只与角的大小有关系,据此进行判断即可.
【解答】解:在锐角△ABC中,如果各边长都缩小为原来的,
那么每个角的大小都不变,
则∠A的正弦值不变,
故选:C.
【点评】本题考查锐角三角函数定义,熟练掌握其定义是解题的关键.
4.(2024秋 莱芜区期末)如图,在Rt△ABC中,∠B=90°,若,AB=BD,则sinC=( )
A. B. C. D.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】设AB=BD=x,可得ADx,根据ADCD,得CD=x,根据勾股定理得ACx,再根据正弦的定义计算即可.
【解答】解:设AB=BD=x,
∵∠B=90°,
∴ADx,
∵ADCD,
∴CD=x,
∴BC=2x,
∴ACx,
∴sinC.
故选:B.
【点评】本题考查了锐角三角函数的定义和勾股定理,熟练掌握锐角三角函数的定义和勾股定理是关键.
5.(2024秋 丽水期末)在Rt△ABC中,∠C=90°,AC=12,BC=5,则tanA的值是( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】根据正切的定义即可求解.
【解答】解:在Rt△ABC中,∠C=90°,AC=12,BC=5,
∴,
故选:A.
【点评】本题考查了锐角三角函数的定义,解答本题的关键要熟练掌握正切的定义:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
二.填空题(共5小题)
6.(2024秋 梁溪区校级期末)如图,△ABC中,∠C=90°,AC=4,BC=3,则sinA的值为 .
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;几何直观;运算能力.
【答案】.
【分析】利用勾股定理求得AB的长,然后根据正弦的定义即可求得答案.
【解答】解:∵△ABC中,∠C=90°,AC=4,BC=3,
∴AB5,
∴sinA,
故答案为:.
【点评】本题考查锐角三角函数定义,勾股定理,熟练掌握其定义是解题的关键.
7.(2024秋 市北区期末)在△ABC中,∠C=90°,AC=6,,则BC= .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】利用锐角三角函数定义计算即可.
【解答】解:∵∠C=90°,tanB,
∴,
∵AC=6,
∴BC.
故答案为:.
【点评】此题主要考查了锐角三角函数定义,正确把握其定义是解题关键.
8.(2024秋 嵊州市期末)在Rt△ABC中,∠ACB=90°,AC=3,AB=5,则sin∠B的值是 .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】根据锐角的正弦值的定义解决此题.
【解答】解:在Rt△ABC中,∠ACB=90°,AC=3,AB=5,
则sin∠B.
故答案为:.
【点评】本题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是解决本题的关键.
9.(2025 闵行区一模)在Rt△ABC中,∠C=90°,AB=10,cosA,那么直角边AC长为 4 .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】4.
【分析】根据余弦定义求解即可.
【解答】解:∵∠C=90°,AB=10,cosA,
∴,
∴AC=4.
故答案为:4.
【点评】此题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是解题的关键.
10.(2024秋 肇源县期中)如图,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】取格点D,连接AD,BD,勾股定理求得AC,进而根据正弦的定义,即可求解.
【解答】解:如图所示,取格点D,连接AD,BD,
由条件可知AC=5,
∴,
故答案为:.
【点评】本题考查了网格与勾股定理,求正弦,熟练掌握以上知识点是关键.
三.解答题(共5小题)
11.(2023秋 洋县期末)如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cosA和tanA的值.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】cosA,tanA.
【分析】先利用勾股定理计算出AC,然后根据余弦和正切的定义求解.
【解答】解:∵∠C=90°,AB=8,BC=4,
∴AC4,
∴cosA,
tanA.
【点评】本题考查了锐角三角函数的定义:正确连接正切和余弦的定义是解决问题的关键.
12.(2024秋 桃源县校级期中)如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC.
(1)求sin∠BAC的值.
(2)求点B到直线MC的距离.
【考点】锐角三角函数的定义;点到直线的距离;勾股定理.
【专题】几何图形;运算能力.
【答案】(1)sin∠BAC;
(2)BE.
【分析】利用勾股定理求出BC,再求出sin∠BAC.过B向MC作垂线,利用正玄函数求BE.
【解答】解:(1)如图:
在Rt△ABC中,
BC5.
sin∠BAC;
(2)作BE⊥MC,垂足是E,
BE=BC sin∠BCE,
∴BE=5.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
13.(2024秋 肇源县期中)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
【考点】锐角三角函数的定义.
【答案】见试题解答内容
【分析】根据勾股定理,可得AB的长,根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
【解答】解:在Rt△ABC中,由勾股定理,得
AB.
sinA,
cosA,
tanA.
【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
14.(2024 红桥区模拟)如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sinC,cosC,tanC的值.
【考点】锐角三角函数的定义.
【专题】等腰三角形与直角三角形;几何直观;运算能力.
【答案】sinC;cosC;tanC.
【分析】利用勾股定理求得BC,然后根据锐角三角函数定义即可求得答案.
【解答】解:∵Rt△ABC中,∠A=90°,AB=3,AC=4,
∴BC5,
则sinC;cosC;tanC.
【点评】本题考查勾股定理及锐角三角函数定义,此为基础且重要知识点,必须熟练掌握.
15.(2024 秦都区校级一模)在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b,求∠B;
(2)已知c=12,sinA,求b.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;应用意识.
【答案】(1)45°;
(2)8.
【分析】根据直角三角形的边角关系求解即可.
【解答】解:(1)∵sinB,
∴∠B=45°;
(2)∵c=12,sinA,
∴a=4,
∴b8,
【点评】本题考查直角三角形的边角关系,掌握直角三角形的边角关系是正确解答的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 金东区期末)在Rt△ABC中,∠C=90°,AB=2,AC=1,则sinA的值为( )
A. B. C. D.
2.(2024秋 泉港区期末)如图,在Rt△ABC中,∠C=90°,下列结论中正确的是( )
A. B. C. D.
3.(2025 崇明区一模)在锐角△ABC中,如果各边长都缩小为原来的,那么∠A的正弦值( )
A.扩大为原来的2倍 B.缩小为原来的
C.大小不变 D.不能确定
4.(2024秋 莱芜区期末)如图,在Rt△ABC中,∠B=90°,若,AB=BD,则sinC=( )
A. B. C. D.
5.(2024秋 丽水期末)在Rt△ABC中,∠C=90°,AC=12,BC=5,则tanA的值是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 梁溪区校级期末)如图,△ABC中,∠C=90°,AC=4,BC=3,则sinA的值为 .
7.(2024秋 市北区期末)在△ABC中,∠C=90°,AC=6,,则BC= .
8.(2024秋 嵊州市期末)在Rt△ABC中,∠ACB=90°,AC=3,AB=5,则sin∠B的值是 .
9.(2025 闵行区一模)在Rt△ABC中,∠C=90°,AB=10,cosA,那么直角边AC长为 .
10.(2024秋 肇源县期中)如图,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
三.解答题(共5小题)
11.(2023秋 洋县期末)如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cosA和tanA的值.
12.(2024秋 桃源县校级期中)如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC.
(1)求sin∠BAC的值.
(2)求点B到直线MC的距离.
13.(2024秋 肇源县期中)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
14.(2024 红桥区模拟)如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sinC,cosC,tanC的值.
15.(2024 秦都区校级一模)在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b,求∠B;
(2)已知c=12,sinA,求b.
中考押题卷:锐角三角函数
参考答案与试题解析
题号 1 2 3 4 5
答案 D D C B A
一.选择题(共5小题)
1.(2024秋 金东区期末)在Rt△ABC中,∠C=90°,AB=2,AC=1,则sinA的值为( )
A. B. C. D.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】先根据勾股定理计算出BC,然后利用正弦的定义求解即可.
【解答】解:∵∠C=90°,AB=2,AC=1,
∴BC,
∴sinA.
故选:D.
【点评】本题考查了锐角三角函数的定义和勾股定理,牢记锐角三角函数的定义是解题的关键.
2.(2024秋 泉港区期末)如图,在Rt△ABC中,∠C=90°,下列结论中正确的是( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】根据正切与余弦的定义,即可解答.
【解答】解:在Rt△ABC中,∠C=90°,cosA,tanA,
故选:D.
【点评】本题考查了锐角三角函数的定义,熟练掌握正切与余弦的定义是解题的关键.
3.(2025 崇明区一模)在锐角△ABC中,如果各边长都缩小为原来的,那么∠A的正弦值( )
A.扩大为原来的2倍 B.缩小为原来的
C.大小不变 D.不能确定
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;推理能力.
【答案】C
【分析】锐角三角函数值只与角的大小有关系,据此进行判断即可.
【解答】解:在锐角△ABC中,如果各边长都缩小为原来的,
那么每个角的大小都不变,
则∠A的正弦值不变,
故选:C.
【点评】本题考查锐角三角函数定义,熟练掌握其定义是解题的关键.
4.(2024秋 莱芜区期末)如图,在Rt△ABC中,∠B=90°,若,AB=BD,则sinC=( )
A. B. C. D.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】设AB=BD=x,可得ADx,根据ADCD,得CD=x,根据勾股定理得ACx,再根据正弦的定义计算即可.
【解答】解:设AB=BD=x,
∵∠B=90°,
∴ADx,
∵ADCD,
∴CD=x,
∴BC=2x,
∴ACx,
∴sinC.
故选:B.
【点评】本题考查了锐角三角函数的定义和勾股定理,熟练掌握锐角三角函数的定义和勾股定理是关键.
5.(2024秋 丽水期末)在Rt△ABC中,∠C=90°,AC=12,BC=5,则tanA的值是( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】根据正切的定义即可求解.
【解答】解:在Rt△ABC中,∠C=90°,AC=12,BC=5,
∴,
故选:A.
【点评】本题考查了锐角三角函数的定义,解答本题的关键要熟练掌握正切的定义:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
二.填空题(共5小题)
6.(2024秋 梁溪区校级期末)如图,△ABC中,∠C=90°,AC=4,BC=3,则sinA的值为 .
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;几何直观;运算能力.
【答案】.
【分析】利用勾股定理求得AB的长,然后根据正弦的定义即可求得答案.
【解答】解:∵△ABC中,∠C=90°,AC=4,BC=3,
∴AB5,
∴sinA,
故答案为:.
【点评】本题考查锐角三角函数定义,勾股定理,熟练掌握其定义是解题的关键.
7.(2024秋 市北区期末)在△ABC中,∠C=90°,AC=6,,则BC= .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】利用锐角三角函数定义计算即可.
【解答】解:∵∠C=90°,tanB,
∴,
∵AC=6,
∴BC.
故答案为:.
【点评】此题主要考查了锐角三角函数定义,正确把握其定义是解题关键.
8.(2024秋 嵊州市期末)在Rt△ABC中,∠ACB=90°,AC=3,AB=5,则sin∠B的值是 .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】根据锐角的正弦值的定义解决此题.
【解答】解:在Rt△ABC中,∠ACB=90°,AC=3,AB=5,
则sin∠B.
故答案为:.
【点评】本题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是解决本题的关键.
9.(2025 闵行区一模)在Rt△ABC中,∠C=90°,AB=10,cosA,那么直角边AC长为 4 .
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】4.
【分析】根据余弦定义求解即可.
【解答】解:∵∠C=90°,AB=10,cosA,
∴,
∴AC=4.
故答案为:4.
【点评】此题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是解题的关键.
10.(2024秋 肇源县期中)如图,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】取格点D,连接AD,BD,勾股定理求得AC,进而根据正弦的定义,即可求解.
【解答】解:如图所示,取格点D,连接AD,BD,
由条件可知AC=5,
∴,
故答案为:.
【点评】本题考查了网格与勾股定理,求正弦,熟练掌握以上知识点是关键.
三.解答题(共5小题)
11.(2023秋 洋县期末)如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cosA和tanA的值.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】cosA,tanA.
【分析】先利用勾股定理计算出AC,然后根据余弦和正切的定义求解.
【解答】解:∵∠C=90°,AB=8,BC=4,
∴AC4,
∴cosA,
tanA.
【点评】本题考查了锐角三角函数的定义:正确连接正切和余弦的定义是解决问题的关键.
12.(2024秋 桃源县校级期中)如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC.
(1)求sin∠BAC的值.
(2)求点B到直线MC的距离.
【考点】锐角三角函数的定义;点到直线的距离;勾股定理.
【专题】几何图形;运算能力.
【答案】(1)sin∠BAC;
(2)BE.
【分析】利用勾股定理求出BC,再求出sin∠BAC.过B向MC作垂线,利用正玄函数求BE.
【解答】解:(1)如图:
在Rt△ABC中,
BC5.
sin∠BAC;
(2)作BE⊥MC,垂足是E,
BE=BC sin∠BCE,
∴BE=5.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
13.(2024秋 肇源县期中)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
【考点】锐角三角函数的定义.
【答案】见试题解答内容
【分析】根据勾股定理,可得AB的长,根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
【解答】解:在Rt△ABC中,由勾股定理,得
AB.
sinA,
cosA,
tanA.
【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
14.(2024 红桥区模拟)如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sinC,cosC,tanC的值.
【考点】锐角三角函数的定义.
【专题】等腰三角形与直角三角形;几何直观;运算能力.
【答案】sinC;cosC;tanC.
【分析】利用勾股定理求得BC,然后根据锐角三角函数定义即可求得答案.
【解答】解:∵Rt△ABC中,∠A=90°,AB=3,AC=4,
∴BC5,
则sinC;cosC;tanC.
【点评】本题考查勾股定理及锐角三角函数定义,此为基础且重要知识点,必须熟练掌握.
15.(2024 秦都区校级一模)在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边.
(1)已知c=2,b,求∠B;
(2)已知c=12,sinA,求b.
【考点】锐角三角函数的定义;勾股定理.
【专题】解直角三角形及其应用;应用意识.
【答案】(1)45°;
(2)8.
【分析】根据直角三角形的边角关系求解即可.
【解答】解:(1)∵sinB,
∴∠B=45°;
(2)∵c=12,sinA,
∴a=4,
∴b8,
【点评】本题考查直角三角形的边角关系,掌握直角三角形的边角关系是正确解答的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
