【中考押题卷】2025年北师大版中考数学考前冲刺:三角函数的应用(含解析)
文档属性
| 名称 | 【中考押题卷】2025年北师大版中考数学考前冲刺:三角函数的应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:27:31 | ||
图片预览


文档简介
中考押题卷:三角函数的应用
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,云南省博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
2.(2025 崇明区一模)如果斜坡的坡度,那么斜坡的坡角等于( )
A.15° B.30° C.45° D.60°
3.(2025 潍坊模拟)在凡尔纳的小说《神秘岛》中,有一段工程师和赫伯特一起测量瞭望塔的高度的情节.工程师先做了一个悬垂,其实就是在绳子的一端栓了一块石头,工程师让赫伯特拿着,然后拿起一根木杆,长度大概为12英尺,两个人一前一后向瞭望塔走去,两个人来到距离瞭望塔485英尺的一个地方,工程师把木杆的一头插到土里,插下去的深度大概是2英尺,接着,工程师从赫伯特手里结果悬垂,对木杆进行校正,知道木杆完全竖直,之后对木杆插到土里的部分进行固定,固定好木杆后,工程师朝着远离木杆的方向走了15英尺,仰面平躺在了地面上(眼睛离木杆15英尺),并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端,工程师在这个点上做了一个标记,如图所示,请你求出此时瞭望塔的高度是( )
A.333英尺 B.英尺 C.400英尺 D.英尺
4.(2024秋 洛阳期末)小明带妹妹玩秋千,当秋千OA停止不动时,踏板与地面的距离AB=0.3米.小明推了一把,秋千OA旋转到OC位置,踏板与地面的距离CD=1.1米.已知tan∠AOC=0.75,则秋千顶O与地面距离OB=( )米.
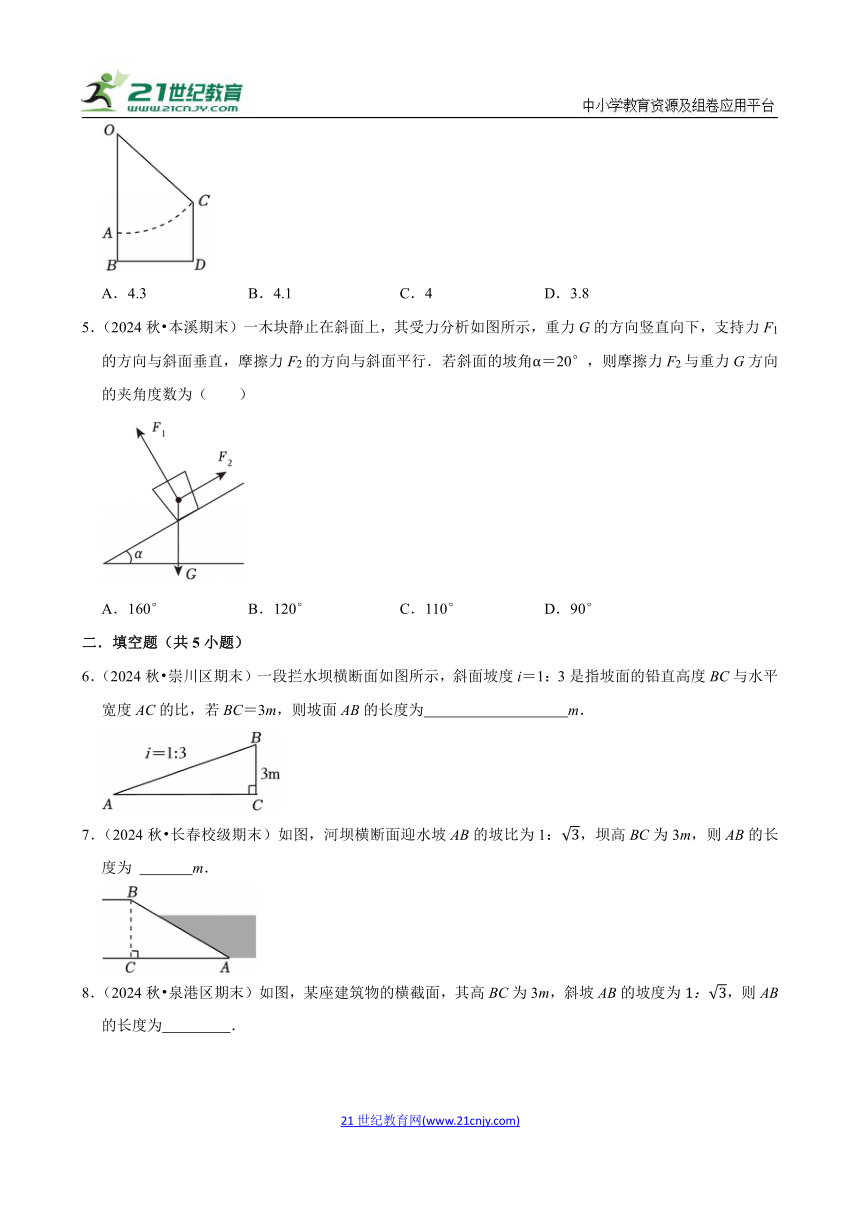
A.4.3 B.4.1 C.4 D.3.8
5.(2024秋 本溪期末)一木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=20°,则摩擦力F2与重力G方向的夹角度数为( )
A.160° B.120° C.110° D.90°
二.填空题(共5小题)
6.(2024秋 崇川区期末)一段拦水坝横断面如图所示,斜面坡度i=1:3是指坡面的铅直高度BC与水平宽度AC的比,若BC=3m,则坡面AB的长度为 m.
7.(2024秋 长春校级期末)如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为3m,则AB的长度为 m.
8.(2024秋 泉港区期末)如图,某座建筑物的横截面,其高BC为3m,斜坡AB的坡度为,则AB的长度为 .
9.(2024秋 中原区期末)昼漏听初发,阳光望渐分.某商店安装遮阳棚(如图①),侧面如图②所示,遮阳棚展开长度MN=2m,遮阳棚前端自然下垂边的长度NC=0.3m,遮阳棚到固定点A的高度AM=3m,遮阳棚与墙面的夹角∠NMA=60°,某时刻的太阳光线与地面的夹角∠CDB=60°(如图③),则遮阳棚在地面上的遮挡宽度AD的长约为 米.(,精确到0.1米)
10.(2024秋 泉州期末)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4分米,OB=15分米,∠BOE=60°,则点C到水平线l的距离CF为 分米(结果保留根号).
三.解答题(共5小题)
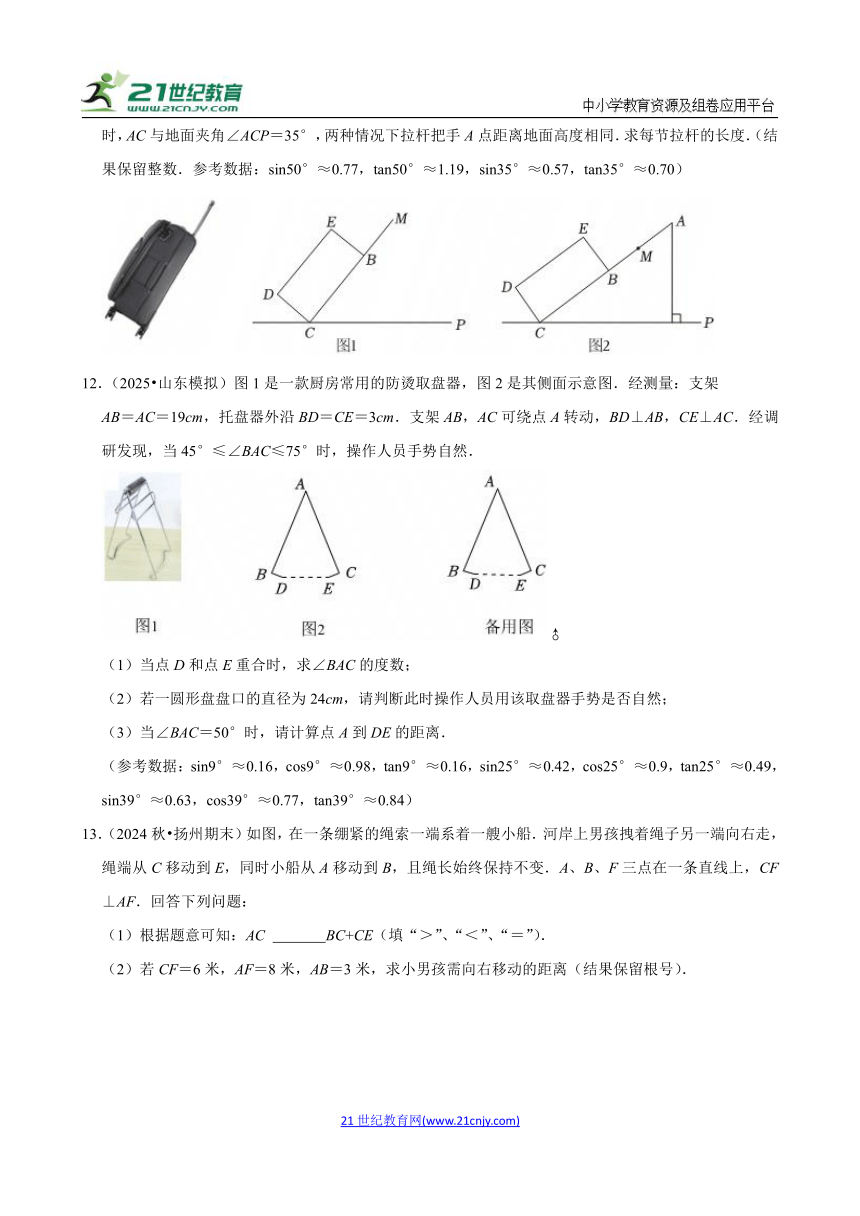
11.(2024秋 仪征市期末)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC的长度为50cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACP=50°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACP=35°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(结果保留整数.参考数据:sin50°≈0.77,tan50°≈1.19,sin35°≈0.57,tan35°≈0.70)
12.(2025 山东模拟)图1是一款厨房常用的防烫取盘器,图2是其侧面示意图.经测量:支架
AB=AC=19cm,托盘器外沿BD=CE=3cm.支架AB,AC可绕点A转动,BD⊥AB,CE⊥AC.经调研发现,当45°≤∠BAC≤75°时,操作人员手势自然.
♂
(1)当点D和点E重合时,求∠BAC的度数;
(2)若一圆形盘盘口的直径为24cm,请判断此时操作人员用该取盘器手势是否自然;
(3)当∠BAC=50°时,请计算点A到DE的距离.
(参考数据:sin9°≈0.16,cos9°≈0.98,tan9°≈0.16,sin25°≈0.42,cos25°≈0.9,tan25°≈0.49,sin39°≈0.63,cos39°≈0.77,tan39°≈0.84)
13.(2024秋 扬州期末)如图,在一条绷紧的绳索一端系着一艘小船.河岸上男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.A、B、F三点在一条直线上,CF⊥AF.回答下列问题:
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=6米,AF=8米,AB=3米,求小男孩需向右移动的距离(结果保留根号).
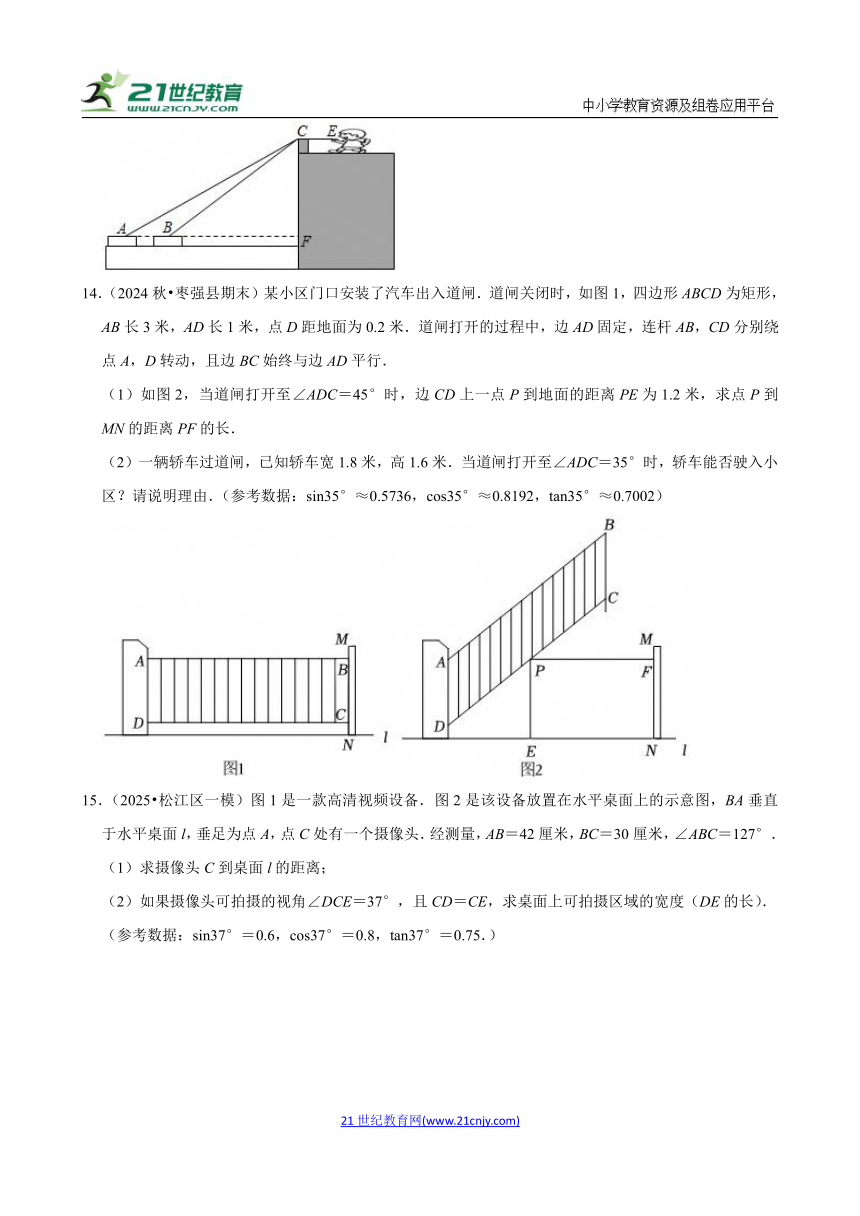
14.(2024秋 枣强县期末)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长3米,AD长1米,点D距地面为0.2米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=45°时,边CD上一点P到地面的距离PE为1.2米,求点P到MN的距离PF的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至∠ADC=35°时,轿车能否驶入小区?请说明理由.(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
15.(2025 松江区一模)图1是一款高清视频设备.图2是该设备放置在水平桌面上的示意图,BA垂直于水平桌面l,垂足为点A,点C处有一个摄像头.经测量,AB=42厘米,BC=30厘米,∠ABC=127°.
(1)求摄像头C到桌面l的距离;
(2)如果摄像头可拍摄的视角∠DCE=37°,且CD=CE,求桌面上可拍摄区域的宽度(DE的长).
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75.)
中考押题卷:三角函数的应用
参考答案与试题解析
题号 1 2 3 4 5
答案 A B B A C
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,云南省博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】A
【分析】直接根据可得结论.
【解答】解:AB的长为12米,AB与AC的夹角为α,
∴在Rt△ABC中,,
∴BC=12sinα(米).
故选:A.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角形函数的定义是解答本题的关键.
2.(2025 崇明区一模)如果斜坡的坡度,那么斜坡的坡角等于( )
A.15° B.30° C.45° D.60°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】坡度=坡角的正切值,据此直接解答.
【解答】解:∵i=tanα,
∴α=30°,
故选:B.
【点评】此题考查的是坡度和坡角的关系,坡角的正切等于坡度,坡角越大,坡度也越大,坡面越陡.
3.(2025 潍坊模拟)在凡尔纳的小说《神秘岛》中,有一段工程师和赫伯特一起测量瞭望塔的高度的情节.工程师先做了一个悬垂,其实就是在绳子的一端栓了一块石头,工程师让赫伯特拿着,然后拿起一根木杆,长度大概为12英尺,两个人一前一后向瞭望塔走去,两个人来到距离瞭望塔485英尺的一个地方,工程师把木杆的一头插到土里,插下去的深度大概是2英尺,接着,工程师从赫伯特手里结果悬垂,对木杆进行校正,知道木杆完全竖直,之后对木杆插到土里的部分进行固定,固定好木杆后,工程师朝着远离木杆的方向走了15英尺,仰面平躺在了地面上(眼睛离木杆15英尺),并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端,工程师在这个点上做了一个标记,如图所示,请你求出此时瞭望塔的高度是( )
A.333英尺 B.英尺 C.400英尺 D.英尺
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】B
【分析】由题意作图,AB为瞭望塔,DE为木杆,工程师在C点,求出BC,DE的长,再根据三角函数即可求解.
【解答】解:由题意可作图如下:AB为瞭望塔,DE为木杆,工程师在C点,
则有BE=485英尺,CE=15英尺,
∴BC=BE+CE=500英尺,
∵木杆有2英尺插入了土中,
∴DE=12﹣2=10(英尺),
∵AB⊥BC,DE⊥BC,
∴,
则,
解得:,
即瞭望塔高度为英尺,
故选:B.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角形函数的定义是解题的关键.
4.(2024秋 洛阳期末)小明带妹妹玩秋千,当秋千OA停止不动时,踏板与地面的距离AB=0.3米.小明推了一把,秋千OA旋转到OC位置,踏板与地面的距离CD=1.1米.已知tan∠AOC=0.75,则秋千顶O与地面距离OB=( )米.
A.4.3 B.4.1 C.4 D.3.8
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】过点C作CE⊥OB,垂足为E,根据题意可得:DC=BE=1.1米,然后在Rt△OEC中,利用锐角三角函数的定义可设EC=3x米,则OE=4x米,从而利用勾股定理可得OC=5x(米),最后根据OA=OC,利用关于x的方程,进行计算即可解答.
【解答】解:过点C作CE⊥OB,垂足为E,
由题意得:DC=BE=1.1米,
在Rt△OEC中,tan∠AOC0.75,
∴设EC=3x米,则OE=4x米,
∴OC5x(米),
∵OA=OC,
∴OE+EB﹣AB=OC,
∴4x+1.1﹣0.3=5x,
解得:x=0.8,
∴OA=OC=5x=4(米),
∴OB=OA+AB=4+0.3=4.3(米),
∴秋千顶O与地面距离OB为4.3米,
故选:A.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
5.(2024秋 本溪期末)一木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=20°,则摩擦力F2与重力G方向的夹角度数为( )
A.160° B.120° C.110° D.90°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据平行线的性质得到∠3=90°,根据三角形的内角和定理得到∠α+∠1=90°,求得∠2=∠1=90°﹣20°=70°,根据平行线的性质即可得到结论.
【解答】解:如图,
由题意可得:
∠3=90°,
∵重力G的方向竖直向下,
∴∠α+∠1=90°,
∴∠2=∠1=90°﹣20°=70°,
∵摩擦力F2的方向与斜面平行,
∴∠β+∠2=180°,
∴∠β=180°﹣∠2=180°﹣70°=110°,
故选:C.
【点评】本题考查了平行线的性质,正确进行计算是解题关键.
二.填空题(共5小题)
6.(2024秋 崇川区期末)一段拦水坝横断面如图所示,斜面坡度i=1:3是指坡面的铅直高度BC与水平宽度AC的比,若BC=3m,则坡面AB的长度为 3 m.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】3.
【分析】根据坡度的概念求出AC,根据勾股定理计算即可.
【解答】解:∵坡AB的斜坡坡度i=1:3,
∴,即,
解得AC=9,
由勾股定理得,AB3(米),
故答案为:3.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握坡度的概念,熟记锐角三角函数的定义是解题的关键.
7.(2024秋 长春校级期末)如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为3m,则AB的长度为 6 m.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】6.
【分析】根据坡度的概念求出AC,再根据勾股定理求出AB.
【解答】解:∵迎水坡AB的坡比为1:,
∴BC:AC=1:,
∵BC=3m,
∴AC=3m,
由勾股定理得:AB6(m),
gu答案为:6.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
8.(2024秋 泉港区期末)如图,某座建筑物的横截面,其高BC为3m,斜坡AB的坡度为,则AB的长度为 6m .
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】6m.
【分析】根据坡度与坡角的关系求出∠A,再根据含30°角的直角三角形的性质解答即可.
【解答】解:∵斜坡AB的坡度为1:,
∴tanA,
∴∠A=30°,
∴AB=2BC=2×=6(m),
故答案为:6m.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记坡度i与坡角α之间的关系为i=tanα是解题的关键.
9.(2024秋 中原区期末)昼漏听初发,阳光望渐分.某商店安装遮阳棚(如图①),侧面如图②所示,遮阳棚展开长度MN=2m,遮阳棚前端自然下垂边的长度NC=0.3m,遮阳棚到固定点A的高度AM=3m,遮阳棚与墙面的夹角∠NMA=60°,某时刻的太阳光线与地面的夹角∠CDB=60°(如图③),则遮阳棚在地面上的遮挡宽度AD的长约为 0.7 米.(,精确到0.1米)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】0.7.
【分析】过点N作NE⊥AM,垂足为E,根据题意可得:∠ABC=90°,AE=BN,EN=AB,然后在Rt△MEN中,利用锐角三角函数的定义求出EM和EN的长,从而求出AE的长,进而求出BC的长,最后在Rt△CDB中,利用锐角三角函数的定义求出BD的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:过点N作NE⊥AM,垂足为E,
由题意得:∠ABC=90°,AE=BN,EN=AB,
在Rt△MEN中,∠NMA=60°,MN=2m,
∴EM=MN cos60°=21(m),
EN=MN sin60°=2(m),
∴EN=ABm,
∵AM=3m,
∴AE=BN=AM﹣EM=3﹣1=2(m),
∵CN=0.3m,
∴CB=NB﹣CN=2﹣0.3=1.7(m),
在Rt△CDB中,∠CDB=60°,
∴BD(m),
∴AD=AB﹣BD0.7(m),
故答案为:0.7.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024秋 泉州期末)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4分米,OB=15分米,∠BOE=60°,则点C到水平线l的距离CF为 (2) 分米(结果保留根号).
【考点】解直角三角形的应用;勾股定理的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(2).
【分析】延长DC交直线l于点G,根据垂直定义可得:∠ABG=∠EOG=90°,从而可得:∠BOG=90°﹣∠BOE=30°,再利用直角三角形的两个锐角互余,∠CGF=60°,然后在Rt△BOG中,利用锐角三角函数的定义求出BG的长,从而求出CG的长,最后在Rt△CGF中,利用锐角三角函数的定义求出CF的长,即可解答.
【解答】解:延长DC交直线l于点G,
∵AB⊥CD,OE⊥l,
∴∠ABG=∠EOG=90°,
∵∠BOE=60°,
∴∠BOG=90°﹣∠BOE=30°,
∴∠CGF=90°﹣∠BOG=60°,
在Rt△BOG中,BO=15分米,
∴BG=BO tan30°=155(分米),
∵BC=4分米,
∴CG=BG﹣BC=(54)分米,
在Rt△CGF中,CF=CG sin60°=(54)(2)分米,
∴点C到水平线l的距离CF为(2)分米,
故答案为:(2).
【点评】本题考查了解直角三角形的应用,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共5小题)
11.(2024秋 仪征市期末)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC的长度为50cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACP=50°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACP=35°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(结果保留整数.参考数据:sin50°≈0.77,tan50°≈1.19,sin35°≈0.57,tan35°≈0.70)
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】过点M作MN⊥CP于N,设每节拉杆的长度为x cm,根据正弦的定义用x分别表示出MN、AH,根据题意列出方程,解方程得到答案.
【解答】解:如图1,过点M作MN⊥CP于N,
设每节拉杆的长度为x cm,则CM=(50+x)cm,CA=(50+2x)cm,
如图1,在Rt△MCN中,∠MCN=50°,
∵sin∠MCN,
∴MN=CM sin∠MCN≈0.77(50+x)cm,
如图2,在Rt△ACH中,∠ACH=35°,
∵sin∠ACH,
∴AH=AC sin∠ACH≈0.57(50+2x)cm,
由题意得:0.77(50+x)=0.57(50+2x),
解得:x≈27,
答:每节拉杆的长度约为27cm.
【点评】本题考查的是解直角三角形的应用﹣坡度坡度问题,熟记锐角三角函数的定义是解题的关键.
12.(2025 山东模拟)图1是一款厨房常用的防烫取盘器,图2是其侧面示意图.经测量:支架
AB=AC=19cm,托盘器外沿BD=CE=3cm.支架AB,AC可绕点A转动,BD⊥AB,CE⊥AC.经调研发现,当45°≤∠BAC≤75°时,操作人员手势自然.
♂
(1)当点D和点E重合时,求∠BAC的度数;
(2)若一圆形盘盘口的直径为24cm,请判断此时操作人员用该取盘器手势是否自然;
(3)当∠BAC=50°时,请计算点A到DE的距离.
(参考数据:sin9°≈0.16,cos9°≈0.98,tan9°≈0.16,sin25°≈0.42,cos25°≈0.9,tan25°≈0.49,sin39°≈0.63,cos39°≈0.77,tan39°≈0.84)
【考点】解直角三角形的应用.
【专题】数形结合;应用意识.
【答案】(1)∠BAC=18°;
(2)此时操作人员用该取盘器手势不自然,理由见解答部分;
(3)点A到DE的距离约为18.36cm.
【分析】(1)连接AD,AE,易得∠BAD的正弦值,根据参考数据可得∠BAD的度数,同理可得∠CAE的度数,相加即为点D和点E重合时∠BAC的度数;
(2)连接BC,易得BC为24cm,过点A作AH⊥BC于点H,易得∠BAH的正弦值,根据参考数据可得∠BAH的大小,进而可得∠BAC的度数,根据手势自然时∠BAC的范围可得操作人员用该取盘器手势是否自然;
(3)过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,分别求出DF和AG的长度,相加即为点A到DE的距离.
【解答】解:(1)连接AD,AE,
∵BD⊥AB,
∴∠ABD=90°,
∵BD=3cm,AB=19cm,
∴tan∠BAD0.16,
∴∠BAD=9°,
同理:∠CAE=9°,
∵点D和点E重合,
∴∠BAC=18°;
(2)连接BC,过点A作AH⊥BC于点H,
∵AB=AC,BC=24cm,
∴BHBC=12cm,
∴sin∠BAH0.63,
∴∠BAH=39°,
∴∠BAC=78°>75°,
∴此时操作人员用该取盘器手势不自然;
(3)过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,
∴∠AGB=90°.
∵AB=AC,∠BAC=50°,
∴∠BAG=25°,
∴AG=AB cos25°≈19×0.9=17.1cm,∠ABG=75°,
∵∠ABD=90°,
∴∠DBF=25°,
∴DF=BD sin25°≈3×0.42=1.26cm,
∴点A到DE的距离为17.1+1.26=18.36cm.
答:点A到DE的距离约为18.36cm.
【点评】本题考查解直角三角形的应用.结合所给条件,把相关线段和角整理到合适的直角三角形中利用锐角三角函数的知识解决问题是解题的关键.
13.(2024秋 扬州期末)如图,在一条绷紧的绳索一端系着一艘小船.河岸上男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.A、B、F三点在一条直线上,CF⊥AF.回答下列问题:
(1)根据题意可知:AC = BC+CE(填“>”、“<”、“=”).
(2)若CF=6米,AF=8米,AB=3米,求小男孩需向右移动的距离(结果保留根号).
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力;应用意识.
【答案】(1)=;
(2)(10)米.
【分析】(1)由绳长始终保持不变即可求解;
(2)由勾股定理求出AC、BC的长,即可解决问题.
【解答】解:(1)∵AC的长度是男孩未拽之前的绳子长,(BC+CE)的长度是男孩拽之后的绳子长,绳长始终保持不变,
∴AC=BC+CE,
故答案为:=;
(2)连接AB,如图所示:
则点A、B、F三点共线,
在Rt△CFA中,由勾股定理得:AC10(米),
∵BF=AF﹣AB=8﹣3=5(米),
在Rt△CFB中,由勾股定理得:BC(米),
由(1)得:AC=BC+CE,
∴CE=AC﹣BC=(10)(米),
∴小男孩需向右移动的距离为(10)米.
【点评】本题考查了解直角三角形的应用,由勾股定理求出AC、BC的长是解题的关键.
14.(2024秋 枣强县期末)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长3米,AD长1米,点D距地面为0.2米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=45°时,边CD上一点P到地面的距离PE为1.2米,求点P到MN的距离PF的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至∠ADC=35°时,轿车能否驶入小区?请说明理由.(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】(1)在Rt△PDQ中,由∠PDQ=45°,DQ=PQ=1,进而求出FP即可;
(2)当∠ADC=36°,PE=1.6米时,求出PF,与1.8米比较即可得出答案.
【解答】解:(1)如图,过点D作DQ⊥PE,垂足为Q,
由题意可知,∠ADC=45°,PE=1.2米,QE=0.2米,
在 Rt△PDQ 中,∠PDQ=45°,PQ=1.2﹣0.2=1(米),
∴DQ=PQ=1 (米),
∴PF=AB﹣DQ=3﹣1=2 (米),
即点P到MN的距离PF的长为2米;
(2)当∠ADC=35°,PE=1.6米时,
则∠DPQ=35°,
PQ=1.6﹣0.2=1.4(米),
∴DQ=PQ tan35°≈1.4×0.7002=0.9803(米),
∴PF=3﹣0.9803≈2.02(米),
∵2.02>1.8,
∴能通过.
【点评】本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.
15.(2025 松江区一模)图1是一款高清视频设备.图2是该设备放置在水平桌面上的示意图,BA垂直于水平桌面l,垂足为点A,点C处有一个摄像头.经测量,AB=42厘米,BC=30厘米,∠ABC=127°.
(1)求摄像头C到桌面l的距离;
(2)如果摄像头可拍摄的视角∠DCE=37°,且CD=CE,求桌面上可拍摄区域的宽度(DE的长).
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75.)
【考点】解直角三角形的应用;视点、视角和盲区.
【专题】数形结合;面积法;运算能力;应用意识.
【答案】(1)摄像头C到桌面l的距离约为60cm;
(2)桌面上可拍摄区域的宽度约为40cm.
【分析】(1)作CH⊥AE于点H,BF⊥CH于点F,可得四边形ABFH是矩形,易得∠CBF的度数,根据∠CBF的正弦值可得CF的长,加上AB的长,即为摄像头C到桌面l的距离;
(2)作EM⊥CD于点M,则∠CME=∠DME=90°,CE为x厘米,则CD=x厘米,根据37°的正弦值和余弦值可得CM和ME的值,进而可得DM的值,那么根据勾股定理可得ED的值,根据△CDE面积的不同表示方法可得x的值,即可求得DE的长.
【解答】解:(1)作CH⊥AE于点H,BF⊥CH于点F,
∴∠CHA=∠BFH=∠BFC=90°,
∵BA⊥l,
∴∠BAE=90°,
∴四边形ABFH是矩形,
∴FH=AB=42厘米,∠ABF=90°,
∵∠ABC=127°,
∴∠DBF=37°,
∵BC=30厘米,
∴CF=30×sin37°≈30×0.6=18(厘米),
∴CH=18+42=60(厘米).
答:摄像头C到桌面l的距离约为60cm;
(2)作EM⊥CD于点M,
∴∠CME=∠DME=90°,
设CE为x厘米,则CD=x厘米,
∵∠DCE=37°,
∴ME=0.6x厘米,CM=0.8x厘米,
∴DM=0.2x厘米,
∴DEx厘米,
∵S△DECDE CHDC ME,
∴x×60=x 0.6x,
解得:x1=0(不合题意,舍去),x2=20,
∴CD=40(厘米).
答:桌面上可拍摄区域的宽度约为40cm.
【点评】本题考查解直角三角形的应用.把所给函数值的角度整理到直角三角形中是解决本题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,云南省博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
2.(2025 崇明区一模)如果斜坡的坡度,那么斜坡的坡角等于( )
A.15° B.30° C.45° D.60°
3.(2025 潍坊模拟)在凡尔纳的小说《神秘岛》中,有一段工程师和赫伯特一起测量瞭望塔的高度的情节.工程师先做了一个悬垂,其实就是在绳子的一端栓了一块石头,工程师让赫伯特拿着,然后拿起一根木杆,长度大概为12英尺,两个人一前一后向瞭望塔走去,两个人来到距离瞭望塔485英尺的一个地方,工程师把木杆的一头插到土里,插下去的深度大概是2英尺,接着,工程师从赫伯特手里结果悬垂,对木杆进行校正,知道木杆完全竖直,之后对木杆插到土里的部分进行固定,固定好木杆后,工程师朝着远离木杆的方向走了15英尺,仰面平躺在了地面上(眼睛离木杆15英尺),并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端,工程师在这个点上做了一个标记,如图所示,请你求出此时瞭望塔的高度是( )
A.333英尺 B.英尺 C.400英尺 D.英尺
4.(2024秋 洛阳期末)小明带妹妹玩秋千,当秋千OA停止不动时,踏板与地面的距离AB=0.3米.小明推了一把,秋千OA旋转到OC位置,踏板与地面的距离CD=1.1米.已知tan∠AOC=0.75,则秋千顶O与地面距离OB=( )米.
A.4.3 B.4.1 C.4 D.3.8
5.(2024秋 本溪期末)一木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=20°,则摩擦力F2与重力G方向的夹角度数为( )
A.160° B.120° C.110° D.90°
二.填空题(共5小题)
6.(2024秋 崇川区期末)一段拦水坝横断面如图所示,斜面坡度i=1:3是指坡面的铅直高度BC与水平宽度AC的比,若BC=3m,则坡面AB的长度为 m.
7.(2024秋 长春校级期末)如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为3m,则AB的长度为 m.
8.(2024秋 泉港区期末)如图,某座建筑物的横截面,其高BC为3m,斜坡AB的坡度为,则AB的长度为 .
9.(2024秋 中原区期末)昼漏听初发,阳光望渐分.某商店安装遮阳棚(如图①),侧面如图②所示,遮阳棚展开长度MN=2m,遮阳棚前端自然下垂边的长度NC=0.3m,遮阳棚到固定点A的高度AM=3m,遮阳棚与墙面的夹角∠NMA=60°,某时刻的太阳光线与地面的夹角∠CDB=60°(如图③),则遮阳棚在地面上的遮挡宽度AD的长约为 米.(,精确到0.1米)
10.(2024秋 泉州期末)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4分米,OB=15分米,∠BOE=60°,则点C到水平线l的距离CF为 分米(结果保留根号).
三.解答题(共5小题)
11.(2024秋 仪征市期末)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC的长度为50cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACP=50°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACP=35°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(结果保留整数.参考数据:sin50°≈0.77,tan50°≈1.19,sin35°≈0.57,tan35°≈0.70)
12.(2025 山东模拟)图1是一款厨房常用的防烫取盘器,图2是其侧面示意图.经测量:支架
AB=AC=19cm,托盘器外沿BD=CE=3cm.支架AB,AC可绕点A转动,BD⊥AB,CE⊥AC.经调研发现,当45°≤∠BAC≤75°时,操作人员手势自然.
♂
(1)当点D和点E重合时,求∠BAC的度数;
(2)若一圆形盘盘口的直径为24cm,请判断此时操作人员用该取盘器手势是否自然;
(3)当∠BAC=50°时,请计算点A到DE的距离.
(参考数据:sin9°≈0.16,cos9°≈0.98,tan9°≈0.16,sin25°≈0.42,cos25°≈0.9,tan25°≈0.49,sin39°≈0.63,cos39°≈0.77,tan39°≈0.84)
13.(2024秋 扬州期末)如图,在一条绷紧的绳索一端系着一艘小船.河岸上男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.A、B、F三点在一条直线上,CF⊥AF.回答下列问题:
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=6米,AF=8米,AB=3米,求小男孩需向右移动的距离(结果保留根号).
14.(2024秋 枣强县期末)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长3米,AD长1米,点D距地面为0.2米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=45°时,边CD上一点P到地面的距离PE为1.2米,求点P到MN的距离PF的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至∠ADC=35°时,轿车能否驶入小区?请说明理由.(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
15.(2025 松江区一模)图1是一款高清视频设备.图2是该设备放置在水平桌面上的示意图,BA垂直于水平桌面l,垂足为点A,点C处有一个摄像头.经测量,AB=42厘米,BC=30厘米,∠ABC=127°.
(1)求摄像头C到桌面l的距离;
(2)如果摄像头可拍摄的视角∠DCE=37°,且CD=CE,求桌面上可拍摄区域的宽度(DE的长).
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75.)
中考押题卷:三角函数的应用
参考答案与试题解析
题号 1 2 3 4 5
答案 A B B A C
一.选择题(共5小题)
1.(2024秋 西山区校级期末)如图,云南省博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】A
【分析】直接根据可得结论.
【解答】解:AB的长为12米,AB与AC的夹角为α,
∴在Rt△ABC中,,
∴BC=12sinα(米).
故选:A.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角形函数的定义是解答本题的关键.
2.(2025 崇明区一模)如果斜坡的坡度,那么斜坡的坡角等于( )
A.15° B.30° C.45° D.60°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】坡度=坡角的正切值,据此直接解答.
【解答】解:∵i=tanα,
∴α=30°,
故选:B.
【点评】此题考查的是坡度和坡角的关系,坡角的正切等于坡度,坡角越大,坡度也越大,坡面越陡.
3.(2025 潍坊模拟)在凡尔纳的小说《神秘岛》中,有一段工程师和赫伯特一起测量瞭望塔的高度的情节.工程师先做了一个悬垂,其实就是在绳子的一端栓了一块石头,工程师让赫伯特拿着,然后拿起一根木杆,长度大概为12英尺,两个人一前一后向瞭望塔走去,两个人来到距离瞭望塔485英尺的一个地方,工程师把木杆的一头插到土里,插下去的深度大概是2英尺,接着,工程师从赫伯特手里结果悬垂,对木杆进行校正,知道木杆完全竖直,之后对木杆插到土里的部分进行固定,固定好木杆后,工程师朝着远离木杆的方向走了15英尺,仰面平躺在了地面上(眼睛离木杆15英尺),并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端,工程师在这个点上做了一个标记,如图所示,请你求出此时瞭望塔的高度是( )
A.333英尺 B.英尺 C.400英尺 D.英尺
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】B
【分析】由题意作图,AB为瞭望塔,DE为木杆,工程师在C点,求出BC,DE的长,再根据三角函数即可求解.
【解答】解:由题意可作图如下:AB为瞭望塔,DE为木杆,工程师在C点,
则有BE=485英尺,CE=15英尺,
∴BC=BE+CE=500英尺,
∵木杆有2英尺插入了土中,
∴DE=12﹣2=10(英尺),
∵AB⊥BC,DE⊥BC,
∴,
则,
解得:,
即瞭望塔高度为英尺,
故选:B.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角形函数的定义是解题的关键.
4.(2024秋 洛阳期末)小明带妹妹玩秋千,当秋千OA停止不动时,踏板与地面的距离AB=0.3米.小明推了一把,秋千OA旋转到OC位置,踏板与地面的距离CD=1.1米.已知tan∠AOC=0.75,则秋千顶O与地面距离OB=( )米.
A.4.3 B.4.1 C.4 D.3.8
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】过点C作CE⊥OB,垂足为E,根据题意可得:DC=BE=1.1米,然后在Rt△OEC中,利用锐角三角函数的定义可设EC=3x米,则OE=4x米,从而利用勾股定理可得OC=5x(米),最后根据OA=OC,利用关于x的方程,进行计算即可解答.
【解答】解:过点C作CE⊥OB,垂足为E,
由题意得:DC=BE=1.1米,
在Rt△OEC中,tan∠AOC0.75,
∴设EC=3x米,则OE=4x米,
∴OC5x(米),
∵OA=OC,
∴OE+EB﹣AB=OC,
∴4x+1.1﹣0.3=5x,
解得:x=0.8,
∴OA=OC=5x=4(米),
∴OB=OA+AB=4+0.3=4.3(米),
∴秋千顶O与地面距离OB为4.3米,
故选:A.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
5.(2024秋 本溪期末)一木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=20°,则摩擦力F2与重力G方向的夹角度数为( )
A.160° B.120° C.110° D.90°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据平行线的性质得到∠3=90°,根据三角形的内角和定理得到∠α+∠1=90°,求得∠2=∠1=90°﹣20°=70°,根据平行线的性质即可得到结论.
【解答】解:如图,
由题意可得:
∠3=90°,
∵重力G的方向竖直向下,
∴∠α+∠1=90°,
∴∠2=∠1=90°﹣20°=70°,
∵摩擦力F2的方向与斜面平行,
∴∠β+∠2=180°,
∴∠β=180°﹣∠2=180°﹣70°=110°,
故选:C.
【点评】本题考查了平行线的性质,正确进行计算是解题关键.
二.填空题(共5小题)
6.(2024秋 崇川区期末)一段拦水坝横断面如图所示,斜面坡度i=1:3是指坡面的铅直高度BC与水平宽度AC的比,若BC=3m,则坡面AB的长度为 3 m.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】3.
【分析】根据坡度的概念求出AC,根据勾股定理计算即可.
【解答】解:∵坡AB的斜坡坡度i=1:3,
∴,即,
解得AC=9,
由勾股定理得,AB3(米),
故答案为:3.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握坡度的概念,熟记锐角三角函数的定义是解题的关键.
7.(2024秋 长春校级期末)如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为3m,则AB的长度为 6 m.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】6.
【分析】根据坡度的概念求出AC,再根据勾股定理求出AB.
【解答】解:∵迎水坡AB的坡比为1:,
∴BC:AC=1:,
∵BC=3m,
∴AC=3m,
由勾股定理得:AB6(m),
gu答案为:6.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
8.(2024秋 泉港区期末)如图,某座建筑物的横截面,其高BC为3m,斜坡AB的坡度为,则AB的长度为 6m .
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】6m.
【分析】根据坡度与坡角的关系求出∠A,再根据含30°角的直角三角形的性质解答即可.
【解答】解:∵斜坡AB的坡度为1:,
∴tanA,
∴∠A=30°,
∴AB=2BC=2×=6(m),
故答案为:6m.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记坡度i与坡角α之间的关系为i=tanα是解题的关键.
9.(2024秋 中原区期末)昼漏听初发,阳光望渐分.某商店安装遮阳棚(如图①),侧面如图②所示,遮阳棚展开长度MN=2m,遮阳棚前端自然下垂边的长度NC=0.3m,遮阳棚到固定点A的高度AM=3m,遮阳棚与墙面的夹角∠NMA=60°,某时刻的太阳光线与地面的夹角∠CDB=60°(如图③),则遮阳棚在地面上的遮挡宽度AD的长约为 0.7 米.(,精确到0.1米)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】0.7.
【分析】过点N作NE⊥AM,垂足为E,根据题意可得:∠ABC=90°,AE=BN,EN=AB,然后在Rt△MEN中,利用锐角三角函数的定义求出EM和EN的长,从而求出AE的长,进而求出BC的长,最后在Rt△CDB中,利用锐角三角函数的定义求出BD的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:过点N作NE⊥AM,垂足为E,
由题意得:∠ABC=90°,AE=BN,EN=AB,
在Rt△MEN中,∠NMA=60°,MN=2m,
∴EM=MN cos60°=21(m),
EN=MN sin60°=2(m),
∴EN=ABm,
∵AM=3m,
∴AE=BN=AM﹣EM=3﹣1=2(m),
∵CN=0.3m,
∴CB=NB﹣CN=2﹣0.3=1.7(m),
在Rt△CDB中,∠CDB=60°,
∴BD(m),
∴AD=AB﹣BD0.7(m),
故答案为:0.7.
【点评】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024秋 泉州期末)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4分米,OB=15分米,∠BOE=60°,则点C到水平线l的距离CF为 (2) 分米(结果保留根号).
【考点】解直角三角形的应用;勾股定理的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(2).
【分析】延长DC交直线l于点G,根据垂直定义可得:∠ABG=∠EOG=90°,从而可得:∠BOG=90°﹣∠BOE=30°,再利用直角三角形的两个锐角互余,∠CGF=60°,然后在Rt△BOG中,利用锐角三角函数的定义求出BG的长,从而求出CG的长,最后在Rt△CGF中,利用锐角三角函数的定义求出CF的长,即可解答.
【解答】解:延长DC交直线l于点G,
∵AB⊥CD,OE⊥l,
∴∠ABG=∠EOG=90°,
∵∠BOE=60°,
∴∠BOG=90°﹣∠BOE=30°,
∴∠CGF=90°﹣∠BOG=60°,
在Rt△BOG中,BO=15分米,
∴BG=BO tan30°=155(分米),
∵BC=4分米,
∴CG=BG﹣BC=(54)分米,
在Rt△CGF中,CF=CG sin60°=(54)(2)分米,
∴点C到水平线l的距离CF为(2)分米,
故答案为:(2).
【点评】本题考查了解直角三角形的应用,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共5小题)
11.(2024秋 仪征市期末)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC的长度为50cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACP=50°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACP=35°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(结果保留整数.参考数据:sin50°≈0.77,tan50°≈1.19,sin35°≈0.57,tan35°≈0.70)
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】过点M作MN⊥CP于N,设每节拉杆的长度为x cm,根据正弦的定义用x分别表示出MN、AH,根据题意列出方程,解方程得到答案.
【解答】解:如图1,过点M作MN⊥CP于N,
设每节拉杆的长度为x cm,则CM=(50+x)cm,CA=(50+2x)cm,
如图1,在Rt△MCN中,∠MCN=50°,
∵sin∠MCN,
∴MN=CM sin∠MCN≈0.77(50+x)cm,
如图2,在Rt△ACH中,∠ACH=35°,
∵sin∠ACH,
∴AH=AC sin∠ACH≈0.57(50+2x)cm,
由题意得:0.77(50+x)=0.57(50+2x),
解得:x≈27,
答:每节拉杆的长度约为27cm.
【点评】本题考查的是解直角三角形的应用﹣坡度坡度问题,熟记锐角三角函数的定义是解题的关键.
12.(2025 山东模拟)图1是一款厨房常用的防烫取盘器,图2是其侧面示意图.经测量:支架
AB=AC=19cm,托盘器外沿BD=CE=3cm.支架AB,AC可绕点A转动,BD⊥AB,CE⊥AC.经调研发现,当45°≤∠BAC≤75°时,操作人员手势自然.
♂
(1)当点D和点E重合时,求∠BAC的度数;
(2)若一圆形盘盘口的直径为24cm,请判断此时操作人员用该取盘器手势是否自然;
(3)当∠BAC=50°时,请计算点A到DE的距离.
(参考数据:sin9°≈0.16,cos9°≈0.98,tan9°≈0.16,sin25°≈0.42,cos25°≈0.9,tan25°≈0.49,sin39°≈0.63,cos39°≈0.77,tan39°≈0.84)
【考点】解直角三角形的应用.
【专题】数形结合;应用意识.
【答案】(1)∠BAC=18°;
(2)此时操作人员用该取盘器手势不自然,理由见解答部分;
(3)点A到DE的距离约为18.36cm.
【分析】(1)连接AD,AE,易得∠BAD的正弦值,根据参考数据可得∠BAD的度数,同理可得∠CAE的度数,相加即为点D和点E重合时∠BAC的度数;
(2)连接BC,易得BC为24cm,过点A作AH⊥BC于点H,易得∠BAH的正弦值,根据参考数据可得∠BAH的大小,进而可得∠BAC的度数,根据手势自然时∠BAC的范围可得操作人员用该取盘器手势是否自然;
(3)过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,分别求出DF和AG的长度,相加即为点A到DE的距离.
【解答】解:(1)连接AD,AE,
∵BD⊥AB,
∴∠ABD=90°,
∵BD=3cm,AB=19cm,
∴tan∠BAD0.16,
∴∠BAD=9°,
同理:∠CAE=9°,
∵点D和点E重合,
∴∠BAC=18°;
(2)连接BC,过点A作AH⊥BC于点H,
∵AB=AC,BC=24cm,
∴BHBC=12cm,
∴sin∠BAH0.63,
∴∠BAH=39°,
∴∠BAC=78°>75°,
∴此时操作人员用该取盘器手势不自然;
(3)过点D作DF⊥BC于点F,过点A作AG⊥BC于点G,
∴∠AGB=90°.
∵AB=AC,∠BAC=50°,
∴∠BAG=25°,
∴AG=AB cos25°≈19×0.9=17.1cm,∠ABG=75°,
∵∠ABD=90°,
∴∠DBF=25°,
∴DF=BD sin25°≈3×0.42=1.26cm,
∴点A到DE的距离为17.1+1.26=18.36cm.
答:点A到DE的距离约为18.36cm.
【点评】本题考查解直角三角形的应用.结合所给条件,把相关线段和角整理到合适的直角三角形中利用锐角三角函数的知识解决问题是解题的关键.
13.(2024秋 扬州期末)如图,在一条绷紧的绳索一端系着一艘小船.河岸上男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.A、B、F三点在一条直线上,CF⊥AF.回答下列问题:
(1)根据题意可知:AC = BC+CE(填“>”、“<”、“=”).
(2)若CF=6米,AF=8米,AB=3米,求小男孩需向右移动的距离(结果保留根号).
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力;应用意识.
【答案】(1)=;
(2)(10)米.
【分析】(1)由绳长始终保持不变即可求解;
(2)由勾股定理求出AC、BC的长,即可解决问题.
【解答】解:(1)∵AC的长度是男孩未拽之前的绳子长,(BC+CE)的长度是男孩拽之后的绳子长,绳长始终保持不变,
∴AC=BC+CE,
故答案为:=;
(2)连接AB,如图所示:
则点A、B、F三点共线,
在Rt△CFA中,由勾股定理得:AC10(米),
∵BF=AF﹣AB=8﹣3=5(米),
在Rt△CFB中,由勾股定理得:BC(米),
由(1)得:AC=BC+CE,
∴CE=AC﹣BC=(10)(米),
∴小男孩需向右移动的距离为(10)米.
【点评】本题考查了解直角三角形的应用,由勾股定理求出AC、BC的长是解题的关键.
14.(2024秋 枣强县期末)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形ABCD为矩形,AB长3米,AD长1米,点D距地面为0.2米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.
(1)如图2,当道闸打开至∠ADC=45°时,边CD上一点P到地面的距离PE为1.2米,求点P到MN的距离PF的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至∠ADC=35°时,轿车能否驶入小区?请说明理由.(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】(1)在Rt△PDQ中,由∠PDQ=45°,DQ=PQ=1,进而求出FP即可;
(2)当∠ADC=36°,PE=1.6米时,求出PF,与1.8米比较即可得出答案.
【解答】解:(1)如图,过点D作DQ⊥PE,垂足为Q,
由题意可知,∠ADC=45°,PE=1.2米,QE=0.2米,
在 Rt△PDQ 中,∠PDQ=45°,PQ=1.2﹣0.2=1(米),
∴DQ=PQ=1 (米),
∴PF=AB﹣DQ=3﹣1=2 (米),
即点P到MN的距离PF的长为2米;
(2)当∠ADC=35°,PE=1.6米时,
则∠DPQ=35°,
PQ=1.6﹣0.2=1.4(米),
∴DQ=PQ tan35°≈1.4×0.7002=0.9803(米),
∴PF=3﹣0.9803≈2.02(米),
∵2.02>1.8,
∴能通过.
【点评】本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.
15.(2025 松江区一模)图1是一款高清视频设备.图2是该设备放置在水平桌面上的示意图,BA垂直于水平桌面l,垂足为点A,点C处有一个摄像头.经测量,AB=42厘米,BC=30厘米,∠ABC=127°.
(1)求摄像头C到桌面l的距离;
(2)如果摄像头可拍摄的视角∠DCE=37°,且CD=CE,求桌面上可拍摄区域的宽度(DE的长).
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75.)
【考点】解直角三角形的应用;视点、视角和盲区.
【专题】数形结合;面积法;运算能力;应用意识.
【答案】(1)摄像头C到桌面l的距离约为60cm;
(2)桌面上可拍摄区域的宽度约为40cm.
【分析】(1)作CH⊥AE于点H,BF⊥CH于点F,可得四边形ABFH是矩形,易得∠CBF的度数,根据∠CBF的正弦值可得CF的长,加上AB的长,即为摄像头C到桌面l的距离;
(2)作EM⊥CD于点M,则∠CME=∠DME=90°,CE为x厘米,则CD=x厘米,根据37°的正弦值和余弦值可得CM和ME的值,进而可得DM的值,那么根据勾股定理可得ED的值,根据△CDE面积的不同表示方法可得x的值,即可求得DE的长.
【解答】解:(1)作CH⊥AE于点H,BF⊥CH于点F,
∴∠CHA=∠BFH=∠BFC=90°,
∵BA⊥l,
∴∠BAE=90°,
∴四边形ABFH是矩形,
∴FH=AB=42厘米,∠ABF=90°,
∵∠ABC=127°,
∴∠DBF=37°,
∵BC=30厘米,
∴CF=30×sin37°≈30×0.6=18(厘米),
∴CH=18+42=60(厘米).
答:摄像头C到桌面l的距离约为60cm;
(2)作EM⊥CD于点M,
∴∠CME=∠DME=90°,
设CE为x厘米,则CD=x厘米,
∵∠DCE=37°,
∴ME=0.6x厘米,CM=0.8x厘米,
∴DM=0.2x厘米,
∴DEx厘米,
∵S△DECDE CHDC ME,
∴x×60=x 0.6x,
解得:x1=0(不合题意,舍去),x2=20,
∴CD=40(厘米).
答:桌面上可拍摄区域的宽度约为40cm.
【点评】本题考查解直角三角形的应用.把所给函数值的角度整理到直角三角形中是解决本题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
