甘肃省2025年中考数学模拟测试卷(一)(含答案)
文档属性
| 名称 | 甘肃省2025年中考数学模拟测试卷(一)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:30:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
甘肃省2025年中考数学模拟测试卷(一)
满分:150分 考试时间:120分钟
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各数中,是负数的是( )
A.-2 B. 0 C.3 D.
2.北京时间2024年12月4日,我国申报的“春节——中国人庆祝传统新年的社会实践”被列入联合国教科文组织人类非物质文化遗产代表作名录.至此,我国共有44个项目被列入联合国教科文组织非物质文化遗产名录、名册,总数居世界第一.下图不同字体的“春”字是轴对称图形的是( )
3.如图,O是量角器的中心,P是量角器上一点,透明直尺ABCD的一边AB与量角器的零刻度线重合,OP与CD相交于点E.若量角器上显示∠POB的读数为50°,则∠DEP的度数是( )
A. 50° B. 110° C. 130° D. 140°
4.下列运算正确的是( )
A.a2+a2 =a4 B. 2a2÷a2=a C. a2·a = a D.(a2) =a6
5.如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=70°,D是⊙O上的一点,连接AD,CD,若AD=CD,则∠BAD的度数是( )
A. 20° B. 25° C. 35° D. 55°
6.清朝数学家梅文鼎的著作《方程论》中记载了这样的一个问题:“山田三亩,场地六亩,共折输粮实田四亩七分;又有山田五亩,场地三亩,共折输粮实田五亩五分.问每亩山田折实田多少,每亩场地折实田多少?”大意是:山田3亩,场地6亩,产粮总量相当于实田4.7亩;又有山田5亩,场地3亩,产粮总量相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩,根据题意,可列方程为( )
A. B. C. D.
7.如图,四边形ABCD为正方形,连接AC,以AC为边在AC右侧作等边△ACE,连接DE,若AB=2,则DE的长为( )
A. B. C. D.
8.2025年2月28日,国家统计局发布了《中华人民共和国2024年国民经济和社会发展统计公报》,如图是公报中发布的全国“2020-2024年国内生产总值及其增长速度”统计图.根据统计图提供的信息,下列结论错误的是( )
2020-2024年国内生产总值及其增长速度
A.2020年,我国国内生产总值突破了100万亿元
B.2024年的国内生产总值比2020年的国内生产总值增加了35%以上
C.2021年的国内生产总值增长速度最快,与前一年相比国内生产总值增加了138955亿元
D.2020年到2024年,国内生产总值的增长速度虽然有快有慢,但是国内生产总值始终上升
9.如图1是发现于敦煌藏经洞中的《全天星图》(图中只展示了一部分),又称《敦煌星图甲本》.整幅星象图描绘了超过1300颗星星,其数量远远超过同时期及此后相当长的一段时间内的欧洲星图和星表.《全天星图》中的一种画法便是用直角坐标投影.爱好天文的小慧按全天星图的这种绘图方式将自己观察到的北斗七星画在如图2所示的网格上.建立适当的平面直角坐标系,若表示“摇光”的点的坐标为(-4,2),表示“开阳”的点的坐标为(0,3),则表示“天权”的点(正好在网格的交点上)的坐标为( )
A.(5,-1) B.(5,1) C.( -1,5) D.(1,5)
10.如图1,动点P从矩形ABCD(AD>CD)的点A出发,沿边AD→DC匀速运动,运动到点C时停止.设点P的运动路程为x,△ABP的周长为y,y与x的函数图象如图2所示,则矩形ABCD的面积为( )
A.3 B. 6 C.7 D. 12
二、填空题:本大题共6小题,每小题4分,共24分.
11.因式分解:x3+6x2+9x= .
12.关于x的一元二次方程ax2+3x-1=0有实数根,则a的值可以是 .(写出一个合理的值即可)
13.若一次函数y=kx+4的函数值y随x的增大而减小,则k的取值范围是 .
14.完美五边形是指可以无重叠、无间隙铺满整个平面的五边形.如图,五边形ABCDE是迄今为止人类发现的第15种完美五边形的示意图.其中∠1=∠2=75°,∠3=∠5,∠4=120°,则∠3的度数为 .
15.方胜纹饰是清代宫廷工艺中常用的吉祥图案,由两个菱形压角相叠而成.图1是清代方胜纹暗花缎袄,图2是缎袄上面的方胜纹示意图,菱形ABCD与菱形A'B'C'D'完全相同,中间的四边形EB'FD也是菱形,EF,B'D相交于点M,若∠ABO=30°,AC=6,EF=1,则AE的长为 .
16.如图1是武威“天马之眼”摩天轮,位于凉州植物园东侧天马湖畔,是中国第五大摩天轮,也是西部之最.图2是其示意图,点O是圆心,半径为60米,摩天轮的圆周上均匀地安装了60个座舱(座舱视为圆周上的点),若摩天轮匀速转动一周需要30分钟,小智进入座舱A,摩天轮顺时针转动8分钟后,那么座舱A走过的路程是
米.(结果保留π)
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
18.(6分)解不等式组:
19.(6分)先化简,再求值:,其中a=2.
20.(8分)根据背景素材,探索解决问题.
用尺规求一个数的算术平方根
背景素材 《几何学》是笛卡尔公开发表的唯一数学著作,它标志着代数与几何的第一次完美结合.他在数学研究工作中关注那些需要作特定长度的几何问题,并在《几何学》中指出“仅用尺规可以完成四种算术运算和开平方根”
已知条件 已知线段AB的长为a,延长BA至点C,使AC=1,O为BC的中点
操作步骤 ①以点O为圆心,OB长为半径画圆;②以点A为圆心,AC长为半径画弧,交线段AB于点E;③分别以点C,E为圆心,大于CE长为半径画弧,两弧交线段BC上方于点M;④作直线AM交⊙O的上半部分于点D,即得垂线段AD.所得AD长即为AB长的算术平方根
问题解决
任务一 根据以上信息,请你用直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 求证:AD=
21.(10分)太阳发出的光经过三棱镜折射后,可以形成红、橙、黄、绿、蓝、靛、紫七种色光组成的光带,这是光的色散现象,说明太阳发出的白光是由不同色光组成的.自然界大部分彩色的光都可以通过红、绿、蓝三种颜色的光按照不同比例混合而成,所以这三种色光又被称为“光的三原色”在一次数学课上,老师利用光的三原色设计了一个“配紫色”游戏,如图是两个可以自由转动的转盘,转盘被分成面积相等的三个扇形,分别对应红、绿、蓝三种颜色,转动两个转盘,记下两个转盘指针指向区域的颜色(若指针指向扇形分界线,则需要重新转动),如果转出的两种颜色分别是红色和蓝色,则可以配成紫色.
(1)求转动两个转盘各1次,恰好可以配成紫色的概率;
(2)同时转动两个转盘,分别记下两个转盘指针所指的颜色,若配成紫色,则小智获胜;若颜色相同,则小慧获胜.请说明这个游戏是否公平.
22.(10分)我国古代屋顶建筑的屋顶式样非常丰富,在中国古代建筑中起着至关重要的作用.常见的屋顶种类主要有庑殿顶、歇山顶、硬山顶、悬山顶、攒尖顶、卷棚顶和平顶等,如图1的古代建筑屋顶,被称为悬山顶,它的侧面示意图呈轴对称图形,如图2所示,已知屋檐AE=6米,屋顶E到支点C的距离CE=5.4米,墙体高CF=3.5米,屋面坡角∠ECD=28°,求点A到地面FG的距离.(结果精确到0.1米.参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)春节档热映电影《哪吒之魔童闹海》以其卓越的票房成绩,彰显了中国动画电影的市场潜力.上映九天便登顶中国电影票房总榜榜首,超越诸多热门影片,成为春节档的票房黑马.这部影片不仅在商业上取得了巨大的成功,更是在观众中引发了广泛而深刻的精神共鸣.某部门为了解本市中学生对这部电影所传递的精神内核的感悟情况,随机抽取了该市部分中学生进行问卷调查,规定每人从A.爱与成长;B.文化与创新;C.自我认同与价值;D.友情与信任;E.团队精神五个选项中必须选择且只能选择一个,并将调查结果进行整理、描述和分析.下面给出了部分信息:
根据以上信息,解答下列问题:
(1)表中m= ;
(2)问卷调查中,每个选项选择人数的中位数落在 项(选填“A”“B”“C”“D”“E”);
(3)若该市共有中学生12000名,请估计选择D.友情与信任的中学生有多少人?
(4)根据以上数据,你认为该市中学生对这部电影所传递的哪种精神内核的感悟更深?请说明理由.
24.(10分)如图,一次函数y=ax+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y=(x>0)的图象交于点C(,8),D(n,1)两点。
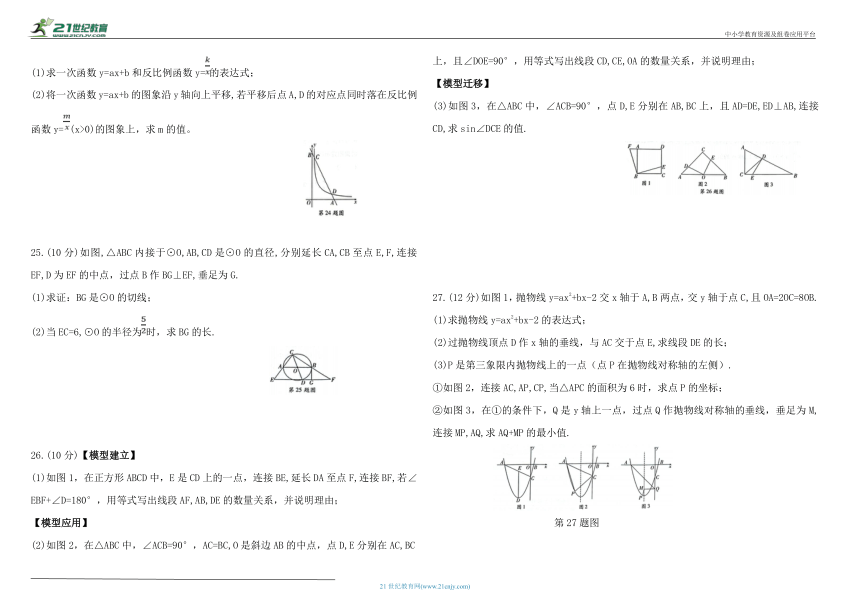
(1)求一次函数y=ax+b和反比例函数y=的表达式;
(2)将一次函数y=ax+b的图象沿y轴向上平移,若平移后点A,D的对应点同时落在反比例函数y=(x>0)的图象上,求m的值。
25.(10分)如图,△ABC内接于⊙O,AB,CD是⊙O的直径,分别延长CA,CB至点E,F,连接EF,D为EF的中点,过点B作BG⊥EF,垂足为G.
(1)求证:BG是⊙O的切线;
(2)当EC=6,⊙O的半径为时,求BG的长.
26.(10分)【模型建立】
(1)如图1,在正方形ABCD中,E是CD上的一点,连接BE,延长DA至点F,连接BF,若∠EBF+∠D=180°,用等式写出线段AF,AB,DE的数量关系,并说明理由;
【模型应用】
(2)如图2,在△ABC中,∠ACB=90°,AC=BC,O是斜边AB的中点,点D,E分别在AC,BC上,且∠DOE=90°,用等式写出线段CD,CE,OA的数量关系,并说明理由;
【模型迁移】
(3)如图3,在△ABC中,∠ACB=90°,点D,E分别在AB,BC上,且AD=DE,ED⊥AB,连接CD,求sin∠DCE的值.
27.(12分)如图1,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.
(1)求抛物线y=ax2+bx-2的表达式;
(2)过抛物线顶点D作x轴的垂线,与AC交于点E,求线段DE的长;
(3)P是第三象限内抛物线上的一点(点P在抛物线对称轴的左侧).
①如图2,连接AC,AP,CP,当△APC的面积为6时,求点P的坐标;
②如图3,在①的条件下,Q是y轴上一点,过点Q作抛物线对称轴的垂线,垂足为M,连接MP,AQ,求AQ+MP的最小值.
第27题图
参考答案
1. A 2. A 3. C 4. D 5. C 6. B 7. D 8. B 9. A 10. D
11.x(x+3)2 12.3(答案不唯一) 13.k<0 14.45° 15.5 16.32π
17.解:原式=…………2分
=……………………4分
=……………………………6分
18.2x-5<3(x-1)
18.解:
解不等式①得,x≥-2,………………2分
解不等式②得,x<1,…………………4分
则不等式组的解集为-2≤x<1.…………6分
19.解:原式=……………2分
=………………………………3分
=.…………………………4分
当a=2时,原式=
20.任务一:解:完成作图如解图1.……………4分
第20题解图
任务二:证明:如解图2,连接CD,BD.……………5分
∵BC是⊙O的直径,
∴∠CDB =90°.
∵DA⊥CB,
∴∠CAD = ∠BAD=90°……………6分
∵∠CDA + ∠ADB = 90°, ∠ADB +∠B = 90°,
∴∠CDA=∠B,
∴△CAD∽△DAB,……………7分
∴
∴
∴ AB=AD2,
∴AD=.........8分
21.解:(1)列表如下……………4分
红 绿 蓝
红 (红,红) (红,绿) (红,蓝)
绿 (绿,红) (绿,绿) (绿,蓝)
蓝 (蓝,红) (蓝,绿) (蓝,蓝)
∵共有9种等可能的情况,其中转出的两种颜色分别是红色和蓝色的情况有2种,
∴恰好可以配成紫色的概率为……………6分
(2)由上表可知,配成紫色的概率为,颜色相同的概率为……………9分
∴P(小智获胜)= P(小慧获胜)=
∵
∴这个游戏不公平.……………10分
22.解:如解图,过点E作EO⊥CD于点O,延长EO交FG于点H,过点A作AI⊥EH于点I. ……………1分
由题意可得∠EAI = ∠ECO =28°,CF =OH=3.5米.
在Rt△EAI中,EI=AE·sin∠EAI=6×sin28°≈2.82(米)……………4分
在Rt△ECO 中,EO = CE·sin∠ECO = 5.4 ×sin28°≈2.538(米),……………7分
∴EH=EO+OH=2.538+3.5=6.038(米),……………9分
∴IH=EH-EI=6.038-2.82=3.218≈3.2(米),
答:点A到地面FG的距离约为3.2米.……………10分
23.解:(1)360...........2分
(2)A. ..............4分
(3)12000×=900(人),
答:估计选择D.友情与信任的中学生有900人..............6分
(4)该市中学生对这部电影所传递的自我认同与价值的感悟更深.理由如下:
因为该市中学生对这部电影所传递的自我认同与价值的选择人数最多,所以该市中学生对这部电影所传递的自我认同与价值的感悟更深.…………8分
24解:(1)把C(,8)代入反比例函数y=中,得k=×8=4
∴反比例函数的表达式为y=…………2分
∵点D(n,1)在反比例函数y=的图象上,
∴1=,解得n=4,∴D(4,1).
把C(,8),D(4,1)代入一次函数y=ax+b中,
得解得
∴一次函数的表达式为y=-2x+9.…………5分
(2)设平移后点A,D的对应点分别为A',D',
∵一次函数的表达式为y=-2x+9,
令y=0,得x=,∴A(,0)…………7分
设一次函数y=-2x+9的图象沿y轴向上平移c个单位长度.则A’(,c),D’(4,1+c)
把A’(,c),D’(4,1+c)分别代入y=y=中
得m=,解得c=8
∴m=4×(1+8)=36......10分
25.(1)证明:如解图,连接BD,∵AB,CD是⊙O的直径,
∴∠ECF=∠CBD=90°,∴BD∥CE. …………1分
∵D为EF的中点,∴B为CF的中点.…………2分
又∵O为CD的中点,
∴OB是△DCF的中位线,∴OB∥EF. ………… 3分
∵BG⊥EF, ∴BG⊥AB.
∵OB是⊙O的半径,…………4分
∴BG是⊙O的切线.…………5分
第25题解图
(2)解:∵⊙O的半径为,∴CD=5.
∵CD是 Rt△ECF斜边的中线,
∴EF=2CD=10,DF=CD=5.…………6分
∵EC = 6,∴CF == 8.
∵B是CF的中点,∴CB=BF=CF=4.
在Rt△BCD中,CD=5,CB=4,
∴BD==3,…………8分
∴S△BDF=BD·BF=BG·DF
∴BG=…………10分
26.解:(1)AF+DE=AB.理由如下:…………1分
∵四边形ABCD是正方形,
∴ ∠ABC = ∠BAD= ∠C = ∠D = 90°,
AB=BC=CD,
∴∠BAF =90°,∠CBE+∠ABE=90°.
∵∠EBF+∠D =180°,∴∠EBF=90°,
∴∠ABF+∠ABE =90°,∴∠ABF =∠CBE.
在△ABF和△CBE中, …………2分
∴ △ABF≌△CBE(ASA),∴ AF=CE.
∵CE+DE=CD,∴AF+DE=AB.………3分
(2)CD+CE=OA.理由如下:
如解图1,连接OC,
∵AC=BC,O为AB的中点,
∴OA=OC=OB,∠A=∠OCE=45°,OC⊥AB,…………4分
∵OD⊥OE,∴∠AOD = ∠COE.
在△AOD和△COE中,..................6分
∴△AOD≌△COE(ASA). ∴ AD = CE,
∴CD+CE=CD+AD=AC=OA.…………7分
第26题解图
(3)如解图2,过点D作DM⊥CD,交BC于点M,由题意可得∠ACB+∠ADE=90°+90°=180°,
∴ ∠A +∠CED=180………… 8分
∵∠DEB + ∠CED = 180°, ∴ ∠A = ∠DEB.
∵∠ADE = ∠CDM = 90°,∴∠ADC =∠EDM.
∵AD = DE,
∴△ACD≌△EMD(ASA).…………9分
∴CD=MD,∴∠DCE =∠DMC=45°.
∴sin∠ECE=sin45°=
27.解:(1)在抛物线y=ax2+bx-2中,令x=0,则y=-2,
∴C(0,-2),
∴OC=2.
∵0A= 20C = 8OB,
∴OA=4,OB=
∴A(-4,0),B(,0)
把点A,B的坐标代入抛物线的表达式,
得
解得
∴抛物线的表达式为y=x2+x-2.…………2分
(2)∵抛物线的表达式为y=x2+x-2=(x+)2-
∴顶点D的坐标为()
设直线AC的表达式为y=mx+n,
把点A,C的坐标代入直线表达式,
得,解得
∴直线AC的表达式为y=-x-2.…………4分
∵点E在直线AC上,
∴点E的坐标为(),
∴DE=
即线段DE的长为.
(3)①如解图1,过点P作PF⊥x轴,交AC于点F,设P(x,x2+x-2)
∴PF=-
∵0A = 4,
S△APC=PF·OA=×(-x2-4x)×4=-2x2-8x.………………6分
∵△APC的面积为6,
∴-2x2-8x=6………………6分
解得x1=-1(舍去),x2=-3,
∴点P的坐标为(-3,-).……………8分
②如解图2,作点A关于y轴的对称点A'(4,0),将点A'向左平移个单位长度(MQ的长度)至点H()…………9分
连接MH,A'Q,PH,则四边形A'HMQ为平行四边形,A'Q=MH=AQ,
∴ AQ + MP = HM + MP,
当点P,M,H三点共线时,AQ+MP有最小值,最小值为PH的长,.........11分
PH=.
即AQ+MP的最小值为…………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
甘肃省2025年中考数学模拟测试卷(一)
满分:150分 考试时间:120分钟
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各数中,是负数的是( )
A.-2 B. 0 C.3 D.
2.北京时间2024年12月4日,我国申报的“春节——中国人庆祝传统新年的社会实践”被列入联合国教科文组织人类非物质文化遗产代表作名录.至此,我国共有44个项目被列入联合国教科文组织非物质文化遗产名录、名册,总数居世界第一.下图不同字体的“春”字是轴对称图形的是( )
3.如图,O是量角器的中心,P是量角器上一点,透明直尺ABCD的一边AB与量角器的零刻度线重合,OP与CD相交于点E.若量角器上显示∠POB的读数为50°,则∠DEP的度数是( )
A. 50° B. 110° C. 130° D. 140°
4.下列运算正确的是( )
A.a2+a2 =a4 B. 2a2÷a2=a C. a2·a = a D.(a2) =a6
5.如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=70°,D是⊙O上的一点,连接AD,CD,若AD=CD,则∠BAD的度数是( )
A. 20° B. 25° C. 35° D. 55°
6.清朝数学家梅文鼎的著作《方程论》中记载了这样的一个问题:“山田三亩,场地六亩,共折输粮实田四亩七分;又有山田五亩,场地三亩,共折输粮实田五亩五分.问每亩山田折实田多少,每亩场地折实田多少?”大意是:山田3亩,场地6亩,产粮总量相当于实田4.7亩;又有山田5亩,场地3亩,产粮总量相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩,根据题意,可列方程为( )
A. B. C. D.
7.如图,四边形ABCD为正方形,连接AC,以AC为边在AC右侧作等边△ACE,连接DE,若AB=2,则DE的长为( )
A. B. C. D.
8.2025年2月28日,国家统计局发布了《中华人民共和国2024年国民经济和社会发展统计公报》,如图是公报中发布的全国“2020-2024年国内生产总值及其增长速度”统计图.根据统计图提供的信息,下列结论错误的是( )
2020-2024年国内生产总值及其增长速度
A.2020年,我国国内生产总值突破了100万亿元
B.2024年的国内生产总值比2020年的国内生产总值增加了35%以上
C.2021年的国内生产总值增长速度最快,与前一年相比国内生产总值增加了138955亿元
D.2020年到2024年,国内生产总值的增长速度虽然有快有慢,但是国内生产总值始终上升
9.如图1是发现于敦煌藏经洞中的《全天星图》(图中只展示了一部分),又称《敦煌星图甲本》.整幅星象图描绘了超过1300颗星星,其数量远远超过同时期及此后相当长的一段时间内的欧洲星图和星表.《全天星图》中的一种画法便是用直角坐标投影.爱好天文的小慧按全天星图的这种绘图方式将自己观察到的北斗七星画在如图2所示的网格上.建立适当的平面直角坐标系,若表示“摇光”的点的坐标为(-4,2),表示“开阳”的点的坐标为(0,3),则表示“天权”的点(正好在网格的交点上)的坐标为( )
A.(5,-1) B.(5,1) C.( -1,5) D.(1,5)
10.如图1,动点P从矩形ABCD(AD>CD)的点A出发,沿边AD→DC匀速运动,运动到点C时停止.设点P的运动路程为x,△ABP的周长为y,y与x的函数图象如图2所示,则矩形ABCD的面积为( )
A.3 B. 6 C.7 D. 12
二、填空题:本大题共6小题,每小题4分,共24分.
11.因式分解:x3+6x2+9x= .
12.关于x的一元二次方程ax2+3x-1=0有实数根,则a的值可以是 .(写出一个合理的值即可)
13.若一次函数y=kx+4的函数值y随x的增大而减小,则k的取值范围是 .
14.完美五边形是指可以无重叠、无间隙铺满整个平面的五边形.如图,五边形ABCDE是迄今为止人类发现的第15种完美五边形的示意图.其中∠1=∠2=75°,∠3=∠5,∠4=120°,则∠3的度数为 .
15.方胜纹饰是清代宫廷工艺中常用的吉祥图案,由两个菱形压角相叠而成.图1是清代方胜纹暗花缎袄,图2是缎袄上面的方胜纹示意图,菱形ABCD与菱形A'B'C'D'完全相同,中间的四边形EB'FD也是菱形,EF,B'D相交于点M,若∠ABO=30°,AC=6,EF=1,则AE的长为 .
16.如图1是武威“天马之眼”摩天轮,位于凉州植物园东侧天马湖畔,是中国第五大摩天轮,也是西部之最.图2是其示意图,点O是圆心,半径为60米,摩天轮的圆周上均匀地安装了60个座舱(座舱视为圆周上的点),若摩天轮匀速转动一周需要30分钟,小智进入座舱A,摩天轮顺时针转动8分钟后,那么座舱A走过的路程是
米.(结果保留π)
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
18.(6分)解不等式组:
19.(6分)先化简,再求值:,其中a=2.
20.(8分)根据背景素材,探索解决问题.
用尺规求一个数的算术平方根
背景素材 《几何学》是笛卡尔公开发表的唯一数学著作,它标志着代数与几何的第一次完美结合.他在数学研究工作中关注那些需要作特定长度的几何问题,并在《几何学》中指出“仅用尺规可以完成四种算术运算和开平方根”
已知条件 已知线段AB的长为a,延长BA至点C,使AC=1,O为BC的中点
操作步骤 ①以点O为圆心,OB长为半径画圆;②以点A为圆心,AC长为半径画弧,交线段AB于点E;③分别以点C,E为圆心,大于CE长为半径画弧,两弧交线段BC上方于点M;④作直线AM交⊙O的上半部分于点D,即得垂线段AD.所得AD长即为AB长的算术平方根
问题解决
任务一 根据以上信息,请你用直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 求证:AD=
21.(10分)太阳发出的光经过三棱镜折射后,可以形成红、橙、黄、绿、蓝、靛、紫七种色光组成的光带,这是光的色散现象,说明太阳发出的白光是由不同色光组成的.自然界大部分彩色的光都可以通过红、绿、蓝三种颜色的光按照不同比例混合而成,所以这三种色光又被称为“光的三原色”在一次数学课上,老师利用光的三原色设计了一个“配紫色”游戏,如图是两个可以自由转动的转盘,转盘被分成面积相等的三个扇形,分别对应红、绿、蓝三种颜色,转动两个转盘,记下两个转盘指针指向区域的颜色(若指针指向扇形分界线,则需要重新转动),如果转出的两种颜色分别是红色和蓝色,则可以配成紫色.
(1)求转动两个转盘各1次,恰好可以配成紫色的概率;
(2)同时转动两个转盘,分别记下两个转盘指针所指的颜色,若配成紫色,则小智获胜;若颜色相同,则小慧获胜.请说明这个游戏是否公平.
22.(10分)我国古代屋顶建筑的屋顶式样非常丰富,在中国古代建筑中起着至关重要的作用.常见的屋顶种类主要有庑殿顶、歇山顶、硬山顶、悬山顶、攒尖顶、卷棚顶和平顶等,如图1的古代建筑屋顶,被称为悬山顶,它的侧面示意图呈轴对称图形,如图2所示,已知屋檐AE=6米,屋顶E到支点C的距离CE=5.4米,墙体高CF=3.5米,屋面坡角∠ECD=28°,求点A到地面FG的距离.(结果精确到0.1米.参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)春节档热映电影《哪吒之魔童闹海》以其卓越的票房成绩,彰显了中国动画电影的市场潜力.上映九天便登顶中国电影票房总榜榜首,超越诸多热门影片,成为春节档的票房黑马.这部影片不仅在商业上取得了巨大的成功,更是在观众中引发了广泛而深刻的精神共鸣.某部门为了解本市中学生对这部电影所传递的精神内核的感悟情况,随机抽取了该市部分中学生进行问卷调查,规定每人从A.爱与成长;B.文化与创新;C.自我认同与价值;D.友情与信任;E.团队精神五个选项中必须选择且只能选择一个,并将调查结果进行整理、描述和分析.下面给出了部分信息:
根据以上信息,解答下列问题:
(1)表中m= ;
(2)问卷调查中,每个选项选择人数的中位数落在 项(选填“A”“B”“C”“D”“E”);
(3)若该市共有中学生12000名,请估计选择D.友情与信任的中学生有多少人?
(4)根据以上数据,你认为该市中学生对这部电影所传递的哪种精神内核的感悟更深?请说明理由.
24.(10分)如图,一次函数y=ax+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y=(x>0)的图象交于点C(,8),D(n,1)两点。
(1)求一次函数y=ax+b和反比例函数y=的表达式;
(2)将一次函数y=ax+b的图象沿y轴向上平移,若平移后点A,D的对应点同时落在反比例函数y=(x>0)的图象上,求m的值。
25.(10分)如图,△ABC内接于⊙O,AB,CD是⊙O的直径,分别延长CA,CB至点E,F,连接EF,D为EF的中点,过点B作BG⊥EF,垂足为G.
(1)求证:BG是⊙O的切线;
(2)当EC=6,⊙O的半径为时,求BG的长.
26.(10分)【模型建立】
(1)如图1,在正方形ABCD中,E是CD上的一点,连接BE,延长DA至点F,连接BF,若∠EBF+∠D=180°,用等式写出线段AF,AB,DE的数量关系,并说明理由;
【模型应用】
(2)如图2,在△ABC中,∠ACB=90°,AC=BC,O是斜边AB的中点,点D,E分别在AC,BC上,且∠DOE=90°,用等式写出线段CD,CE,OA的数量关系,并说明理由;
【模型迁移】
(3)如图3,在△ABC中,∠ACB=90°,点D,E分别在AB,BC上,且AD=DE,ED⊥AB,连接CD,求sin∠DCE的值.
27.(12分)如图1,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.
(1)求抛物线y=ax2+bx-2的表达式;
(2)过抛物线顶点D作x轴的垂线,与AC交于点E,求线段DE的长;
(3)P是第三象限内抛物线上的一点(点P在抛物线对称轴的左侧).
①如图2,连接AC,AP,CP,当△APC的面积为6时,求点P的坐标;
②如图3,在①的条件下,Q是y轴上一点,过点Q作抛物线对称轴的垂线,垂足为M,连接MP,AQ,求AQ+MP的最小值.
第27题图
参考答案
1. A 2. A 3. C 4. D 5. C 6. B 7. D 8. B 9. A 10. D
11.x(x+3)2 12.3(答案不唯一) 13.k<0 14.45° 15.5 16.32π
17.解:原式=…………2分
=……………………4分
=……………………………6分
18.2x-5<3(x-1)
18.解:
解不等式①得,x≥-2,………………2分
解不等式②得,x<1,…………………4分
则不等式组的解集为-2≤x<1.…………6分
19.解:原式=……………2分
=………………………………3分
=.…………………………4分
当a=2时,原式=
20.任务一:解:完成作图如解图1.……………4分
第20题解图
任务二:证明:如解图2,连接CD,BD.……………5分
∵BC是⊙O的直径,
∴∠CDB =90°.
∵DA⊥CB,
∴∠CAD = ∠BAD=90°……………6分
∵∠CDA + ∠ADB = 90°, ∠ADB +∠B = 90°,
∴∠CDA=∠B,
∴△CAD∽△DAB,……………7分
∴
∴
∴ AB=AD2,
∴AD=.........8分
21.解:(1)列表如下……………4分
红 绿 蓝
红 (红,红) (红,绿) (红,蓝)
绿 (绿,红) (绿,绿) (绿,蓝)
蓝 (蓝,红) (蓝,绿) (蓝,蓝)
∵共有9种等可能的情况,其中转出的两种颜色分别是红色和蓝色的情况有2种,
∴恰好可以配成紫色的概率为……………6分
(2)由上表可知,配成紫色的概率为,颜色相同的概率为……………9分
∴P(小智获胜)= P(小慧获胜)=
∵
∴这个游戏不公平.……………10分
22.解:如解图,过点E作EO⊥CD于点O,延长EO交FG于点H,过点A作AI⊥EH于点I. ……………1分
由题意可得∠EAI = ∠ECO =28°,CF =OH=3.5米.
在Rt△EAI中,EI=AE·sin∠EAI=6×sin28°≈2.82(米)……………4分
在Rt△ECO 中,EO = CE·sin∠ECO = 5.4 ×sin28°≈2.538(米),……………7分
∴EH=EO+OH=2.538+3.5=6.038(米),……………9分
∴IH=EH-EI=6.038-2.82=3.218≈3.2(米),
答:点A到地面FG的距离约为3.2米.……………10分
23.解:(1)360...........2分
(2)A. ..............4分
(3)12000×=900(人),
答:估计选择D.友情与信任的中学生有900人..............6分
(4)该市中学生对这部电影所传递的自我认同与价值的感悟更深.理由如下:
因为该市中学生对这部电影所传递的自我认同与价值的选择人数最多,所以该市中学生对这部电影所传递的自我认同与价值的感悟更深.…………8分
24解:(1)把C(,8)代入反比例函数y=中,得k=×8=4
∴反比例函数的表达式为y=…………2分
∵点D(n,1)在反比例函数y=的图象上,
∴1=,解得n=4,∴D(4,1).
把C(,8),D(4,1)代入一次函数y=ax+b中,
得解得
∴一次函数的表达式为y=-2x+9.…………5分
(2)设平移后点A,D的对应点分别为A',D',
∵一次函数的表达式为y=-2x+9,
令y=0,得x=,∴A(,0)…………7分
设一次函数y=-2x+9的图象沿y轴向上平移c个单位长度.则A’(,c),D’(4,1+c)
把A’(,c),D’(4,1+c)分别代入y=y=中
得m=,解得c=8
∴m=4×(1+8)=36......10分
25.(1)证明:如解图,连接BD,∵AB,CD是⊙O的直径,
∴∠ECF=∠CBD=90°,∴BD∥CE. …………1分
∵D为EF的中点,∴B为CF的中点.…………2分
又∵O为CD的中点,
∴OB是△DCF的中位线,∴OB∥EF. ………… 3分
∵BG⊥EF, ∴BG⊥AB.
∵OB是⊙O的半径,…………4分
∴BG是⊙O的切线.…………5分
第25题解图
(2)解:∵⊙O的半径为,∴CD=5.
∵CD是 Rt△ECF斜边的中线,
∴EF=2CD=10,DF=CD=5.…………6分
∵EC = 6,∴CF == 8.
∵B是CF的中点,∴CB=BF=CF=4.
在Rt△BCD中,CD=5,CB=4,
∴BD==3,…………8分
∴S△BDF=BD·BF=BG·DF
∴BG=…………10分
26.解:(1)AF+DE=AB.理由如下:…………1分
∵四边形ABCD是正方形,
∴ ∠ABC = ∠BAD= ∠C = ∠D = 90°,
AB=BC=CD,
∴∠BAF =90°,∠CBE+∠ABE=90°.
∵∠EBF+∠D =180°,∴∠EBF=90°,
∴∠ABF+∠ABE =90°,∴∠ABF =∠CBE.
在△ABF和△CBE中, …………2分
∴ △ABF≌△CBE(ASA),∴ AF=CE.
∵CE+DE=CD,∴AF+DE=AB.………3分
(2)CD+CE=OA.理由如下:
如解图1,连接OC,
∵AC=BC,O为AB的中点,
∴OA=OC=OB,∠A=∠OCE=45°,OC⊥AB,…………4分
∵OD⊥OE,∴∠AOD = ∠COE.
在△AOD和△COE中,..................6分
∴△AOD≌△COE(ASA). ∴ AD = CE,
∴CD+CE=CD+AD=AC=OA.…………7分
第26题解图
(3)如解图2,过点D作DM⊥CD,交BC于点M,由题意可得∠ACB+∠ADE=90°+90°=180°,
∴ ∠A +∠CED=180………… 8分
∵∠DEB + ∠CED = 180°, ∴ ∠A = ∠DEB.
∵∠ADE = ∠CDM = 90°,∴∠ADC =∠EDM.
∵AD = DE,
∴△ACD≌△EMD(ASA).…………9分
∴CD=MD,∴∠DCE =∠DMC=45°.
∴sin∠ECE=sin45°=
27.解:(1)在抛物线y=ax2+bx-2中,令x=0,则y=-2,
∴C(0,-2),
∴OC=2.
∵0A= 20C = 8OB,
∴OA=4,OB=
∴A(-4,0),B(,0)
把点A,B的坐标代入抛物线的表达式,
得
解得
∴抛物线的表达式为y=x2+x-2.…………2分
(2)∵抛物线的表达式为y=x2+x-2=(x+)2-
∴顶点D的坐标为()
设直线AC的表达式为y=mx+n,
把点A,C的坐标代入直线表达式,
得,解得
∴直线AC的表达式为y=-x-2.…………4分
∵点E在直线AC上,
∴点E的坐标为(),
∴DE=
即线段DE的长为.
(3)①如解图1,过点P作PF⊥x轴,交AC于点F,设P(x,x2+x-2)
∴PF=-
∵0A = 4,
S△APC=PF·OA=×(-x2-4x)×4=-2x2-8x.………………6分
∵△APC的面积为6,
∴-2x2-8x=6………………6分
解得x1=-1(舍去),x2=-3,
∴点P的坐标为(-3,-).……………8分
②如解图2,作点A关于y轴的对称点A'(4,0),将点A'向左平移个单位长度(MQ的长度)至点H()…………9分
连接MH,A'Q,PH,则四边形A'HMQ为平行四边形,A'Q=MH=AQ,
∴ AQ + MP = HM + MP,
当点P,M,H三点共线时,AQ+MP有最小值,最小值为PH的长,.........11分
PH=.
即AQ+MP的最小值为…………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
