第十二章 数据的收集、整理与描述 第34讲统计图的综合应用 培优讲义 2024-2025学年人教版七年级数学下册
文档属性
| 名称 | 第十二章 数据的收集、整理与描述 第34讲统计图的综合应用 培优讲义 2024-2025学年人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 320.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 05:56:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
统计图的综合应用
方法技巧
1.条形统计图的特点:反映每组中的具体数据;易于比较数据之间的差别.
2.折线统计图的特点:反映数据的变化趋势.
3.扇形统计图的特点:反映部分在总体中所占百分比.
4.频数分布直方图的特点:频数和频率都能够反映每个对象出现的频繁程度;频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的分布情况.
题型一 条形统计图、折线统计图和扇形统计图的综合应用
【例1】 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形统计图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
【练1】 某校七(2)班班长统计了今年1——8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了折线统计图,下列说法错误的是( )
某班学生1~8月课外阅读数量
折线统计图
A.阅读量最多的是8月份 B.阅读量最少的是6月份
C.3月份和5月份的阅读量相等 D.每月阅读量超过40本的有5个月
题型二 频数分布表与频数分布直方图的综合应用
【例2】 为了掌握八年级数学试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 47.5~59.5 2 0.05
2 59.5~71.5 4 0.10
3 71.5~83.5 a 0.20
4 83.5~95.5 10 0.25
5 95.5~107.5 b C
6 107.5~120 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ;
(2)已知全区八年级共有 200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补全完整频数分布直方图.
针对练习4
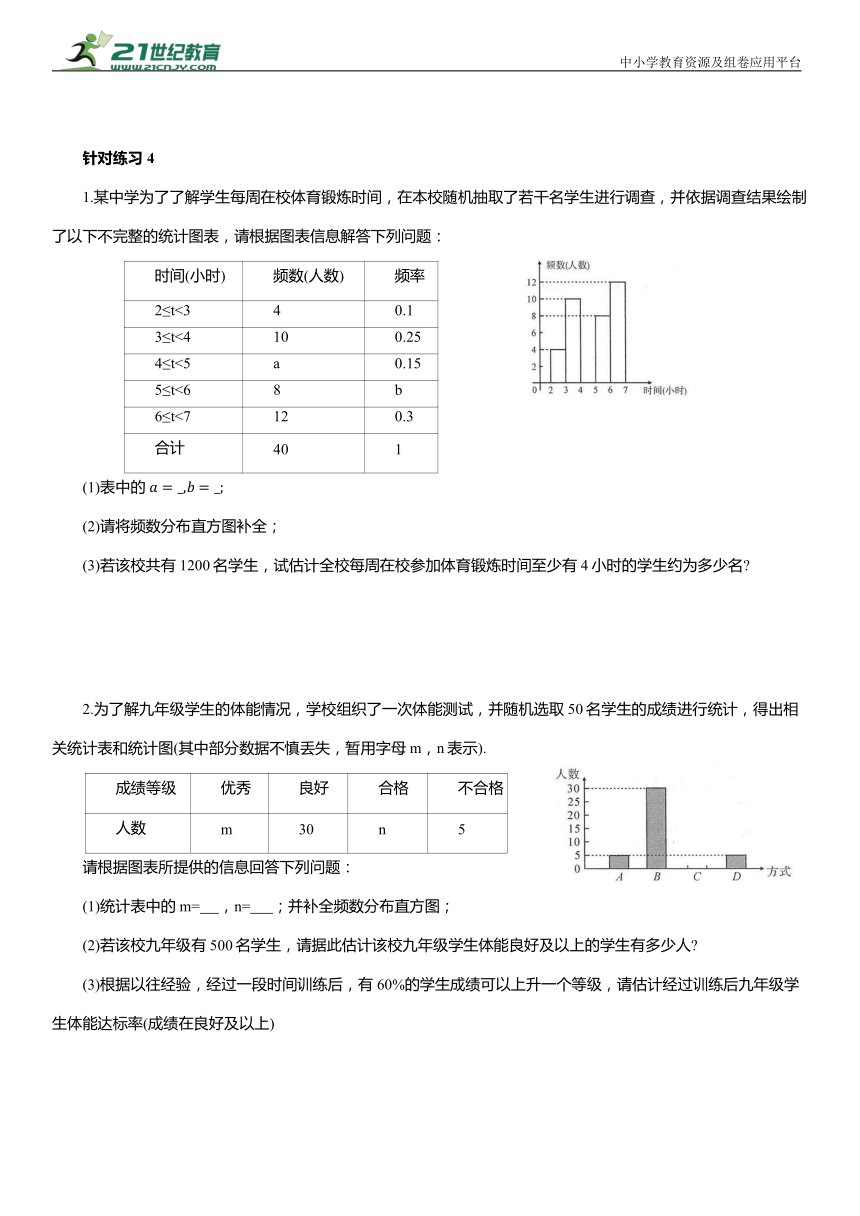
1.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名
2.为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 优秀 良好 合格 不合格
人数 m 30 n 5
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好及以上的学生有多少人
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)
统计图的综合应用
方法技巧
1.条形统计图的特点:反映每组中的具体数据;易于比较数据之间的差别.
2.折线统计图的特点:反映数据的变化趋势.
3.扇形统计图的特点:反映部分在总体中所占百分比.
4.频数分布直方图的特点:频数和频率都能够反映每个对象出现的频繁程度;频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的分布情况.
题型一 条形统计图、折线统计图和扇形统计图的综合应用
【例1】 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( D )
A.本次抽样调查的样本容量是5000
B.扇形统计图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
【分析】 结合条形图和扇形图,求出样本人数,A.本次抽样调查的样本容量是 正确;B.扇形图中的m为10%,正确;C.样本中选择公共交通出行的有5000×50%=2500人,正确;D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,错误.
【解答】 选D.
【练1】 某校七(2)班班长统计了今年1——8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了折线统计图,下列说法错误的是( D)
某班学生1~8月课外阅读数量
折线统计图
A.阅读量最多的是8月份 B.阅读量最少的是6月份
C.3月份和5月份的阅读量相等 D.每月阅读量超过40本的有5个月
题型二 频数分布表与频数分布直方图的综合应用
【例2】 为了掌握八年级数学试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 47.5~59.5 2 0.05
2 59.5~71.5 4 0.10
3 71.5~83.5 a 0.20
4 83.5~95.5 10 0.25
5 95.5~107.5 b C
6 107.5~120 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= 8 ,b= 10 ,c= 0.25 ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 1200 ,72分及以上为及格,预计及格的人数约为 6800 ,及格的百分比约为 85% ;
(3)补全完整频数分布直方图. 某班数学成绩分布直方图
【分析】 (1)根据第一组的频数和频率,再结合频率=频数,可求出总数,继而可分别得出a,b,c的值.(2)根据频率=频数的关系可分别求出各空的答案.(3)根据(1)中a,b的值即可补全图形.
【解答】 (1)∵被调查的总人数为2÷0.05=40人,∴a=40×0.2=8,b=40-(2+4+8+10+6)=10,c=10÷40=0.25,故答案为:8,10,0.25;
(2)∵全区八年级学生总人数为200×40=8000人,∴预计优秀的
人数约为8000×0.15=1200人,预计及格的人数约为8000×(0.20+0.25+0.25+0.15)=6800人,及格的百分比约为 故答案为:1200人,6800人,85%;
(3)补全频数分布直方图略.
针对练习4
1.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名
【解答】 (1)6,0.2;
(2)补全频数分布直方图略;
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1200×(0.15+0.2+0.3)=780名.
2.为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 优秀 良好 合格 不合格
人数 m 30 n 5
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= 5 ,n= 10 ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好及以上的学生有多少人
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)
【解答】 (1)根据条形图可以得到:m=5,n=50-5-30-5=10(人),补全频数分布直方图略;
故答案为:5,10;
(2)估计该校九年级学生体能良好以上的学生有 (人);
(3)(35+10×60%)÷50=82%,
答:估计经过训练后九年级学生体能达标率为82%.
统计图的综合应用
方法技巧
1.条形统计图的特点:反映每组中的具体数据;易于比较数据之间的差别.
2.折线统计图的特点:反映数据的变化趋势.
3.扇形统计图的特点:反映部分在总体中所占百分比.
4.频数分布直方图的特点:频数和频率都能够反映每个对象出现的频繁程度;频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的分布情况.
题型一 条形统计图、折线统计图和扇形统计图的综合应用
【例1】 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形统计图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
【练1】 某校七(2)班班长统计了今年1——8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了折线统计图,下列说法错误的是( )
某班学生1~8月课外阅读数量
折线统计图
A.阅读量最多的是8月份 B.阅读量最少的是6月份
C.3月份和5月份的阅读量相等 D.每月阅读量超过40本的有5个月
题型二 频数分布表与频数分布直方图的综合应用
【例2】 为了掌握八年级数学试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 47.5~59.5 2 0.05
2 59.5~71.5 4 0.10
3 71.5~83.5 a 0.20
4 83.5~95.5 10 0.25
5 95.5~107.5 b C
6 107.5~120 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ;
(2)已知全区八年级共有 200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补全完整频数分布直方图.
针对练习4
1.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名
2.为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 优秀 良好 合格 不合格
人数 m 30 n 5
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好及以上的学生有多少人
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)
统计图的综合应用
方法技巧
1.条形统计图的特点:反映每组中的具体数据;易于比较数据之间的差别.
2.折线统计图的特点:反映数据的变化趋势.
3.扇形统计图的特点:反映部分在总体中所占百分比.
4.频数分布直方图的特点:频数和频率都能够反映每个对象出现的频繁程度;频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的分布情况.
题型一 条形统计图、折线统计图和扇形统计图的综合应用
【例1】 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( D )
A.本次抽样调查的样本容量是5000
B.扇形统计图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
【分析】 结合条形图和扇形图,求出样本人数,A.本次抽样调查的样本容量是 正确;B.扇形图中的m为10%,正确;C.样本中选择公共交通出行的有5000×50%=2500人,正确;D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,错误.
【解答】 选D.
【练1】 某校七(2)班班长统计了今年1——8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了折线统计图,下列说法错误的是( D)
某班学生1~8月课外阅读数量
折线统计图
A.阅读量最多的是8月份 B.阅读量最少的是6月份
C.3月份和5月份的阅读量相等 D.每月阅读量超过40本的有5个月
题型二 频数分布表与频数分布直方图的综合应用
【例2】 为了掌握八年级数学试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 47.5~59.5 2 0.05
2 59.5~71.5 4 0.10
3 71.5~83.5 a 0.20
4 83.5~95.5 10 0.25
5 95.5~107.5 b C
6 107.5~120 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= 8 ,b= 10 ,c= 0.25 ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 1200 ,72分及以上为及格,预计及格的人数约为 6800 ,及格的百分比约为 85% ;
(3)补全完整频数分布直方图. 某班数学成绩分布直方图
【分析】 (1)根据第一组的频数和频率,再结合频率=频数,可求出总数,继而可分别得出a,b,c的值.(2)根据频率=频数的关系可分别求出各空的答案.(3)根据(1)中a,b的值即可补全图形.
【解答】 (1)∵被调查的总人数为2÷0.05=40人,∴a=40×0.2=8,b=40-(2+4+8+10+6)=10,c=10÷40=0.25,故答案为:8,10,0.25;
(2)∵全区八年级学生总人数为200×40=8000人,∴预计优秀的
人数约为8000×0.15=1200人,预计及格的人数约为8000×(0.20+0.25+0.25+0.15)=6800人,及格的百分比约为 故答案为:1200人,6800人,85%;
(3)补全频数分布直方图略.
针对练习4
1.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名
【解答】 (1)6,0.2;
(2)补全频数分布直方图略;
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1200×(0.15+0.2+0.3)=780名.
2.为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 优秀 良好 合格 不合格
人数 m 30 n 5
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= 5 ,n= 10 ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好及以上的学生有多少人
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)
【解答】 (1)根据条形图可以得到:m=5,n=50-5-30-5=10(人),补全频数分布直方图略;
故答案为:5,10;
(2)估计该校九年级学生体能良好以上的学生有 (人);
(3)(35+10×60%)÷50=82%,
答:估计经过训练后九年级学生体能达标率为82%.
同课章节目录
