人教新课标A版选修2-3数学2.4正态分布同步检测
文档属性
| 名称 | 人教新课标A版选修2-3数学2.4正态分布同步检测 | 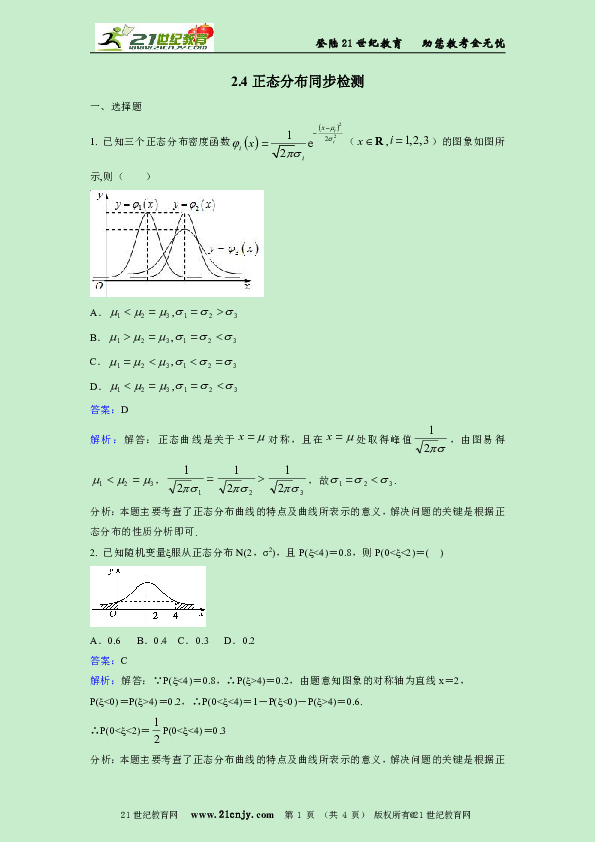 | |
| 格式 | doc | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-16 10:26:12 | ||
图片预览




文档简介
登陆21世纪教育 助您教考全无忧
2.4正态分布同步检测
一、选择题
1. 已知三个正态分布密度函数(,)的图象如图所示,则( )
A.,
B.,
C.,
D.,
答案:D
解析:解答:正态曲线是关于对称,且在处取得峰值,由图易得,,故.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布的性质分析即可.
2. 已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
INCLUDEPICTURE "E:\\WCFUpload\\Upload\\2014-04\\03\\b084998e-0042-4284-8f43-36d45a98f7ef\\L1-6-10.TIF" \* MERGEFORMAT INCLUDEPICTURE "../../../../L1-6-10.TIF" \* MERGEFORMAT
A.0.6 B.0.4 C.0.3 D.0.2
答案:C
解析:解答:∵P(ξ<4)=0.8,∴P(ξ>4)=0.2,由题意知图象的对称轴为直线x=2,
P(ξ<0)=P(ξ>4)=0.2,∴P(0<ξ<4)=1-P(ξ<0)-P(ξ>4)=0.6.
∴P(0<ξ<2)=P(0<ξ<4)=0.3
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布图像的性质结合概率公式计算即可.
3. 设随机变量服从正态分布,若,则( )
A. B. C. D.
答案:B
解析:解答:由已知,,正态曲线的对称轴为,所以,. 选.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布的性质进行分析计算即可解决问题.
4. 若随机变量(1,4),,则=( )
A. B. C. D.
答案:C
解析:解答:由对称性:,
,故选
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据整体分别性质计算即可.
5. 在某项测量中,测量结果 服从正态分布 ,若在(0,2)内取值的概率为0.4,则在(0,+∞)内取值的概率为( )
A.0.2 B.0.4 C.0.8 D.0.9
答案:D
解析:解答:∵ξ服从正态分布∴曲线的对称轴是直线x=2,∵ξ在(0,2)内取值的概率为0.4,∴ξ在(2,+∞)内取值的概率为0.5,∴ξ在(0,+∞)内取值的概率为0.5+0.4=0.9故答案为:D.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给条件分析计算即可.
6. 设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(-1A.p B.1-p C.1-2p D.-p
答案:D
解析:解答:由于随机变量X服从正态分布N(0,1),
图象关于对称,,
因此.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义计算即可.
7. 在某次数学测试中,学生成绩ξ服从正态分布N(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
答案:B
解析:解答:根据正态曲线的对称性可知,ξ在(80,100)内的概率为0.4,因为ξ在(0,100)内的概率为0.5,所以ξ在(0,80)内的概率为0.1,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义分析计算即可.
8. 某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为( )
A.10 B.9 C.8 D.7
答案:B
解析:解答:由已知,正态曲线的对称轴为,
即,
所以该班学生数学成绩在120分以上的人数为.
选.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义计算即可.
9. 我校在模块考试中约有1000人参加考试,其数学考试成绩ξ~N(90,a2)(a>0,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的,则此次数学考试成绩不低于110分的学生人数约为( )
A.600 B.400 C.300 D.200
答案:D
解析:解答:考试成绩在70分到110分之间的人数为600,则落在90分到110分之间的人数为300人,故数学考试成绩不低于110分的学生人数约为500-300=200.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据所给事件满足条件结合正态分布性质计算即可.
10. 某商场经营的一种袋装的大米的质量服从正态分布N,(单位kg).任选一袋这种大米,其质量在9.8~10.2kg的概率为( )
A.0.0456 B.0.6826 C.0.9544 D.0.997
答案:C
解析:解答:.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据根据正态分布的意义进行分析即可.
11. 已知某批零件的长度误差(单位:毫米)服从正态分布,从中随机取一件,其长度误差落在区间(3,6)内的概率为( )
(附:若随机变量ξ服从正态分布 ,则 ,
。)
A.4.56% B.13.59% C.27.18% D.31.74%
答案:B
解析:解答:用表示 零件的长度,根据正态分布的性质得:
, 故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给条件计算即可.
12. 已知某市两次数学测试的成绩和分别服从正态分布和,则以下结论正确的是( )
A.第一次测试的平均分比第二次测试的平均分要高,也比第二次成绩稳定
B.第一次测试的平均分比第二次测试的平均分要高,但不如第二次成绩稳定
C.第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定
D.第二次测试的平均分比第一次测试的平均分要高,但不如第一次成绩稳定
答案:C
解析:解答:第一次测试的平均分,;第二次测试的平均分,,因此第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定,故答案为C.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点结合期望与方差性质分析比较即可.
13. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
A. B. C. D.
答案:B
解析:解答:三个电子元件的使用寿命均服从正态分布,则三个电子元件的使用寿命超过1000小时的概率为,设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时,元件3正常},C={该部件的使用寿命超过1000小时},则,
,故答案选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是正态分布曲线的特点及曲线所表示的意义结合所给事件的性质运用相互独立事件概率公式计算即可.
14. 下列四个判断:
①某校高三(1)班的人和高三(2)班的人数分别是,某次测试数学平均分分别是,则这两个班的数学平均分为;
②从总体中抽取的样本则回归直线必过点;
③已知服从正态分布,且,则
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
答案:B
解析:解答:①的平均分为,所以①错;②必过(3,3.5);对,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给实际问题进行具体分析计算即可.
15. 已知服从正态分布N(,)的随机变量在区间(,),(,),和(,)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
A. 683套 B. 954套 C. 972套 D. 997套
答案:B
解析:解答:由于,服从正态分布N(,)的随机变量在区间(,),(,),和(,)内取值的概率分别为68.3%,95.4%,和99.7%.所以,当学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制套数为1000×95.4%=954,,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行分析计算即可.
二、填空题
16. 已知正态分布密度曲线,且,则方差为 .
答案:2
解析:解答:正态分布密度曲线可知对称轴为=20,所以函数的最大值是,所以,即=,所以方差为2.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行计算即可.
17. .如图是当σ取三个不同值σ1、σ2、σ3时的三种正态曲线N(0,σ2)的图象,那么σ1、σ2、σ3的大小关系是________.
答案:0<σ1<σ2<σ3
解析:解答:由已知得=,∴σ2=1.由正态曲线的性质知,当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,所以0<σ1<σ2=1<σ3.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行比较即可.
18. 已知某次英语考试的成绩X服从正态分布N(116,64),则10000名考生中成绩在140分以上的人数为________.
答案:13
解析:解答:由已知得μ=116,σ=8.
∴P(92<X≤140)=P(μ-3σ<X≤μ+3σ)=0.9974,
∴P(X>140)=(1-0.9974)=0.0013,
∴成绩在140以上的人数为13.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合公式计算即可.
19.已知正态分布总体落在区间(-∞,0.3)的概率为0.5,那么相应的正态曲线φμ,σ(x)在x=________时达到最高点.
答案:0.3
解析:解答:∵P(X<0.3)=0.5,∴P(X≥0.3)=0.5,即x=0.3是正态曲线的对称轴,
∴当x=0.3时φμ,σ(x)达到最高点.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点直接分析判定即可.
20. 设X~N(0,1).
①P(-ε<X<0)=P(0<X<ε);
②P(X<0)=0.5;
③已知P(-1<X<1)=0.6826,
则P(X<-1)=0.1587;
④已知P(-2<X<2)=0.9544,
则P(X<2)=0.9772;
⑤已知P(-3<X<3)=0.9974,
则P(X<3)=0.9987.
其中正确的有________(只填序号).
答案:①②③④⑤
解析:解答:P(X<-1)=(1-P(|X|<1)),
=(1-0.6826)=0.1587,
故③正确;对于④,P(X<2)
=(1-P(|X|<2))+P(|X|<2)
=(1-0.9544)+0.9544=0.9772;
故④正确,同理⑤正确.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是正态分布曲线的特点计算即可.
三、解答题
21. 设X~N(1,22),试求
①P(-1<X≤3);
②P(3<X≤5);
③P(X≥5).
答案:解答:∵X~N(1,22),∴ =1, =2.
①P(-1<X≤3)=P(1-2<X≤1+2)=P(-<X≤+)=0.682 6.
②∵P(3<X≤5)=P(-3<X≤-1)
∴P(3<X≤5)=[P(-3<X≤5)-P(-1<X≤3)]=[P(1-4<X≤1+4)-P(1-2<X≤1+2)]
=[P(-2<X≤+2)-P(-<X≤+)]=×(0.954 4-0.682 6)=0.135 9.
③∵P(X≥5)=P(X≤-3),
∴P(X≥5)= [1-P(-3<X≤5)]=[1-P(1-4<X≤1+4)]
=[1-P(-2<X≤+2)]=(1-0.954 4)=0.022 8.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合概率公式计算即,难度不大,属于基础题目.
22. 若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高(单位:㎝),则该地公共汽车门的高度应设计为多高?
答案:解答:设该地公共汽车门的高度应设计高为cm,则根据题意可知:,由于,
所以,
也即:
通过查表可知:
解得:
即该地公共汽车门至少应设计为189cm高.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是实际应用问题,分析可知:求的是门的最低高度,可设其为,使其总体在不低于的概率值小于1%,即:,从中解出的范围.
23. 某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过
市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布;第二条
路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布.
①若只有70分钟可用,问应走哪条路线?
②若只有65分钟可用,又应走哪条路线
答案:由已知X~, Y~.由正态分布的区间性质
.
然后解决问题的关键是:根据上述性质得到如下结果:
对X:.区间为(30,70〕
对Y:.区间为(52, 68〕要尽量保证用时在(30,70〕: (52, 68〕才能保证有95﹪以上的概率准时到达.
由已知X~, Y~.由正态分布的区间性质
对X:.区间为(30,70〕
对Y:.区间为(52, 68〕要尽量保证用时在(30,70〕: (52, 68〕才能保证有95﹪以上的概率准时到达,
所以①时间只有70分钟可用,应该走第二条路线 ;
②时间只有65分钟可用,两种方案都能能保证有95﹪以上的概率准时到达,
但是走市区平均用时比路线二少了10分钟,应该走第一条路线.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点结合所给事件选取本题的方案计算对应的概率情况进行具体比较分析即可得到结果.
24. 某军区新兵步枪射击个人平均成绩(单位:环)服从正态分布,从这些个人平均成绩中随机抽取个,得到如下频数分布表:
频数
(1)求和的值(用样本数学期望、方差代替总体数学期望、方差);
答案:解:根据条件得随机抽取的100个成绩的分布列为:
4 5 6 7 8 9
频率 0.01 0.02 0.26 0.40 0.29 0.02
∴,
∴
因样本成绩是随机得到,由样本估计总体得,
(2)如果这个军区有新兵名,试估计这个军区新兵步枪射击个人平均成绩在区间上的人数
[参考数据:,若,则,,].
答案:由(1)知,
∵,∴,
∴
所以这个军区新兵50步枪射击个人平均成绩在区间(7.9,8.8]上的人数约为.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是(1)列出频率分布表,用频率代替概率代入期望与方差公式计算即可;(2)由随机变量服从正态分布求出,即可估计相应的人数.
25. 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
(1)求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);
答案:抽取产品的质量指标值的样本平均值和样本方差分别为
,
.
(2)由直方图可以认为,这种产品的质量指标服从正态分布,其中近似为样本平均数,近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间的产品件数.利用(i)的结果,求.
附:
若则,
。
答案:(i)由(1)知,服从正态分布,从而
.
(ii)由(i)可知,一件产品的质量指标值位于区间的概率为,依题意知,所以.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是(1)由频率分布直方图可估计样本特征数众数、中位数、均值、方差.若同一组的数据用该组区间的中点值作代表,则众数为最高矩形中点横坐标.中位数为面积等分为的点.均值为每个矩形中点横坐标与该矩形面积积的累加值.方差是矩形横坐标与均值差的平方的加权平均值.(2)(i)由已知得,,故
;(ii)某用户从该企业购买了100件这种产品,相当于100次独立重复试验,则这100件产品中质量指标值位于区间的产品件数,故期望.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 12 页 (共 12 页) 版权所有@21世纪教育网
2.4正态分布同步检测
一、选择题
1. 已知三个正态分布密度函数(,)的图象如图所示,则( )
A.,
B.,
C.,
D.,
答案:D
解析:解答:正态曲线是关于对称,且在处取得峰值,由图易得,,故.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布的性质分析即可.
2. 已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
INCLUDEPICTURE "E:\\WCFUpload\\Upload\\2014-04\\03\\b084998e-0042-4284-8f43-36d45a98f7ef\\L1-6-10.TIF" \* MERGEFORMAT INCLUDEPICTURE "../../../../L1-6-10.TIF" \* MERGEFORMAT
A.0.6 B.0.4 C.0.3 D.0.2
答案:C
解析:解答:∵P(ξ<4)=0.8,∴P(ξ>4)=0.2,由题意知图象的对称轴为直线x=2,
P(ξ<0)=P(ξ>4)=0.2,∴P(0<ξ<4)=1-P(ξ<0)-P(ξ>4)=0.6.
∴P(0<ξ<2)=P(0<ξ<4)=0.3
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布图像的性质结合概率公式计算即可.
3. 设随机变量服从正态分布,若,则( )
A. B. C. D.
答案:B
解析:解答:由已知,,正态曲线的对称轴为,所以,. 选.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布的性质进行分析计算即可解决问题.
4. 若随机变量(1,4),,则=( )
A. B. C. D.
答案:C
解析:解答:由对称性:,
,故选
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据整体分别性质计算即可.
5. 在某项测量中,测量结果 服从正态分布 ,若在(0,2)内取值的概率为0.4,则在(0,+∞)内取值的概率为( )
A.0.2 B.0.4 C.0.8 D.0.9
答案:D
解析:解答:∵ξ服从正态分布∴曲线的对称轴是直线x=2,∵ξ在(0,2)内取值的概率为0.4,∴ξ在(2,+∞)内取值的概率为0.5,∴ξ在(0,+∞)内取值的概率为0.5+0.4=0.9故答案为:D.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给条件分析计算即可.
6. 设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(-1
答案:D
解析:解答:由于随机变量X服从正态分布N(0,1),
图象关于对称,,
因此.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义计算即可.
7. 在某次数学测试中,学生成绩ξ服从正态分布N(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
答案:B
解析:解答:根据正态曲线的对称性可知,ξ在(80,100)内的概率为0.4,因为ξ在(0,100)内的概率为0.5,所以ξ在(0,80)内的概率为0.1,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义分析计算即可.
8. 某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为( )
A.10 B.9 C.8 D.7
答案:B
解析:解答:由已知,正态曲线的对称轴为,
即,
所以该班学生数学成绩在120分以上的人数为.
选.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义计算即可.
9. 我校在模块考试中约有1000人参加考试,其数学考试成绩ξ~N(90,a2)(a>0,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的,则此次数学考试成绩不低于110分的学生人数约为( )
A.600 B.400 C.300 D.200
答案:D
解析:解答:考试成绩在70分到110分之间的人数为600,则落在90分到110分之间的人数为300人,故数学考试成绩不低于110分的学生人数约为500-300=200.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据所给事件满足条件结合正态分布性质计算即可.
10. 某商场经营的一种袋装的大米的质量服从正态分布N,(单位kg).任选一袋这种大米,其质量在9.8~10.2kg的概率为( )
A.0.0456 B.0.6826 C.0.9544 D.0.997
答案:C
解析:解答:.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据根据正态分布的意义进行分析即可.
11. 已知某批零件的长度误差(单位:毫米)服从正态分布,从中随机取一件,其长度误差落在区间(3,6)内的概率为( )
(附:若随机变量ξ服从正态分布 ,则 ,
。)
A.4.56% B.13.59% C.27.18% D.31.74%
答案:B
解析:解答:用表示 零件的长度,根据正态分布的性质得:
, 故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给条件计算即可.
12. 已知某市两次数学测试的成绩和分别服从正态分布和,则以下结论正确的是( )
A.第一次测试的平均分比第二次测试的平均分要高,也比第二次成绩稳定
B.第一次测试的平均分比第二次测试的平均分要高,但不如第二次成绩稳定
C.第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定
D.第二次测试的平均分比第一次测试的平均分要高,但不如第一次成绩稳定
答案:C
解析:解答:第一次测试的平均分,;第二次测试的平均分,,因此第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定,故答案为C.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点结合期望与方差性质分析比较即可.
13. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
A. B. C. D.
答案:B
解析:解答:三个电子元件的使用寿命均服从正态分布,则三个电子元件的使用寿命超过1000小时的概率为,设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时,元件3正常},C={该部件的使用寿命超过1000小时},则,
,故答案选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是正态分布曲线的特点及曲线所表示的意义结合所给事件的性质运用相互独立事件概率公式计算即可.
14. 下列四个判断:
①某校高三(1)班的人和高三(2)班的人数分别是,某次测试数学平均分分别是,则这两个班的数学平均分为;
②从总体中抽取的样本则回归直线必过点;
③已知服从正态分布,且,则
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
答案:B
解析:解答:①的平均分为,所以①错;②必过(3,3.5);对,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合所给实际问题进行具体分析计算即可.
15. 已知服从正态分布N(,)的随机变量在区间(,),(,),和(,)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
A. 683套 B. 954套 C. 972套 D. 997套
答案:B
解析:解答:由于,服从正态分布N(,)的随机变量在区间(,),(,),和(,)内取值的概率分别为68.3%,95.4%,和99.7%.所以,当学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制套数为1000×95.4%=954,,故选B.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行分析计算即可.
二、填空题
16. 已知正态分布密度曲线,且,则方差为 .
答案:2
解析:解答:正态分布密度曲线可知对称轴为=20,所以函数的最大值是,所以,即=,所以方差为2.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行计算即可.
17. .如图是当σ取三个不同值σ1、σ2、σ3时的三种正态曲线N(0,σ2)的图象,那么σ1、σ2、σ3的大小关系是________.
答案:0<σ1<σ2<σ3
解析:解答:由已知得=,∴σ2=1.由正态曲线的性质知,当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,所以0<σ1<σ2=1<σ3.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义进行比较即可.
18. 已知某次英语考试的成绩X服从正态分布N(116,64),则10000名考生中成绩在140分以上的人数为________.
答案:13
解析:解答:由已知得μ=116,σ=8.
∴P(92<X≤140)=P(μ-3σ<X≤μ+3σ)=0.9974,
∴P(X>140)=(1-0.9974)=0.0013,
∴成绩在140以上的人数为13.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合公式计算即可.
19.已知正态分布总体落在区间(-∞,0.3)的概率为0.5,那么相应的正态曲线φμ,σ(x)在x=________时达到最高点.
答案:0.3
解析:解答:∵P(X<0.3)=0.5,∴P(X≥0.3)=0.5,即x=0.3是正态曲线的对称轴,
∴当x=0.3时φμ,σ(x)达到最高点.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点直接分析判定即可.
20. 设X~N(0,1).
①P(-ε<X<0)=P(0<X<ε);
②P(X<0)=0.5;
③已知P(-1<X<1)=0.6826,
则P(X<-1)=0.1587;
④已知P(-2<X<2)=0.9544,
则P(X<2)=0.9772;
⑤已知P(-3<X<3)=0.9974,
则P(X<3)=0.9987.
其中正确的有________(只填序号).
答案:①②③④⑤
解析:解答:P(X<-1)=(1-P(|X|<1)),
=(1-0.6826)=0.1587,
故③正确;对于④,P(X<2)
=(1-P(|X|<2))+P(|X|<2)
=(1-0.9544)+0.9544=0.9772;
故④正确,同理⑤正确.
分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是正态分布曲线的特点计算即可.
三、解答题
21. 设X~N(1,22),试求
①P(-1<X≤3);
②P(3<X≤5);
③P(X≥5).
答案:解答:∵X~N(1,22),∴ =1, =2.
①P(-1<X≤3)=P(1-2<X≤1+2)=P(-<X≤+)=0.682 6.
②∵P(3<X≤5)=P(-3<X≤-1)
∴P(3<X≤5)=[P(-3<X≤5)-P(-1<X≤3)]=[P(1-4<X≤1+4)-P(1-2<X≤1+2)]
=[P(-2<X≤+2)-P(-<X≤+)]=×(0.954 4-0.682 6)=0.135 9.
③∵P(X≥5)=P(X≤-3),
∴P(X≥5)= [1-P(-3<X≤5)]=[1-P(1-4<X≤1+4)]
=[1-P(-2<X≤+2)]=(1-0.954 4)=0.022 8.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点及曲线所表示的意义结合概率公式计算即,难度不大,属于基础题目.
22. 若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高(单位:㎝),则该地公共汽车门的高度应设计为多高?
答案:解答:设该地公共汽车门的高度应设计高为cm,则根据题意可知:,由于,
所以,
也即:
通过查表可知:
解得:
即该地公共汽车门至少应设计为189cm高.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是实际应用问题,分析可知:求的是门的最低高度,可设其为,使其总体在不低于的概率值小于1%,即:,从中解出的范围.
23. 某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过
市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布;第二条
路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布.
①若只有70分钟可用,问应走哪条路线?
②若只有65分钟可用,又应走哪条路线
答案:由已知X~, Y~.由正态分布的区间性质
.
然后解决问题的关键是:根据上述性质得到如下结果:
对X:.区间为(30,70〕
对Y:.区间为(52, 68〕要尽量保证用时在(30,70〕: (52, 68〕才能保证有95﹪以上的概率准时到达.
由已知X~, Y~.由正态分布的区间性质
对X:.区间为(30,70〕
对Y:.区间为(52, 68〕要尽量保证用时在(30,70〕: (52, 68〕才能保证有95﹪以上的概率准时到达,
所以①时间只有70分钟可用,应该走第二条路线 ;
②时间只有65分钟可用,两种方案都能能保证有95﹪以上的概率准时到达,
但是走市区平均用时比路线二少了10分钟,应该走第一条路线.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是根据正态分布曲线的特点结合所给事件选取本题的方案计算对应的概率情况进行具体比较分析即可得到结果.
24. 某军区新兵步枪射击个人平均成绩(单位:环)服从正态分布,从这些个人平均成绩中随机抽取个,得到如下频数分布表:
频数
(1)求和的值(用样本数学期望、方差代替总体数学期望、方差);
答案:解:根据条件得随机抽取的100个成绩的分布列为:
4 5 6 7 8 9
频率 0.01 0.02 0.26 0.40 0.29 0.02
∴,
∴
因样本成绩是随机得到,由样本估计总体得,
(2)如果这个军区有新兵名,试估计这个军区新兵步枪射击个人平均成绩在区间上的人数
[参考数据:,若,则,,].
答案:由(1)知,
∵,∴,
∴
所以这个军区新兵50步枪射击个人平均成绩在区间(7.9,8.8]上的人数约为.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是(1)列出频率分布表,用频率代替概率代入期望与方差公式计算即可;(2)由随机变量服从正态分布求出,即可估计相应的人数.
25. 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
(1)求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);
答案:抽取产品的质量指标值的样本平均值和样本方差分别为
,
.
(2)由直方图可以认为,这种产品的质量指标服从正态分布,其中近似为样本平均数,近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间的产品件数.利用(i)的结果,求.
附:
若则,
。
答案:(i)由(1)知,服从正态分布,从而
.
(ii)由(i)可知,一件产品的质量指标值位于区间的概率为,依题意知,所以.
解析:分析:本题主要考查了正态分布曲线的特点及曲线所表示的意义,解决问题的关键是(1)由频率分布直方图可估计样本特征数众数、中位数、均值、方差.若同一组的数据用该组区间的中点值作代表,则众数为最高矩形中点横坐标.中位数为面积等分为的点.均值为每个矩形中点横坐标与该矩形面积积的累加值.方差是矩形横坐标与均值差的平方的加权平均值.(2)(i)由已知得,,故
;(ii)某用户从该企业购买了100件这种产品,相当于100次独立重复试验,则这100件产品中质量指标值位于区间的产品件数,故期望.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 12 页 (共 12 页) 版权所有@21世纪教育网
