教科版高中物理选择性必修第二册第二章电磁感应及其应用2法拉第电磁感应定律课件(49页ppt)
文档属性
| 名称 | 教科版高中物理选择性必修第二册第二章电磁感应及其应用2法拉第电磁感应定律课件(49页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-15 00:00:00 | ||
图片预览











文档简介
(共49张PPT)
第二章 电磁感应及其应用
2.法拉第电磁感应定律
第*页
研习任务一 法拉第电磁感应定律
合作 讨论
如图所示,将条形磁铁从同一高度插入线圈中,快速插入和缓慢插入有什么相 同和不同?
提示:同样的磁体、同样的线圈匝数,磁体穿过线圈的过程中线圈磁通量的变化量是相同的,但是磁体穿过的时间不同,从而磁通量的变化快慢不同,即磁通量的变化率不同.
教材 认知
1. 感应电动势
(2)在电磁感应现象中,闭合回路中的感应电流由感应电动势和回路的电阻决定.
电磁感应
电源
感应电动势
变化率
伏
特(V)
项目 磁通量Ф 磁通量的变化量ΔФ
物理
意义 某时刻穿过磁场中某个面的磁感线条数 在某一过程中穿过某个面 的磁通量的变化量 穿过某个面的磁通量变 化的快慢
当B、S互相垂直时大小计算 Ф=BS
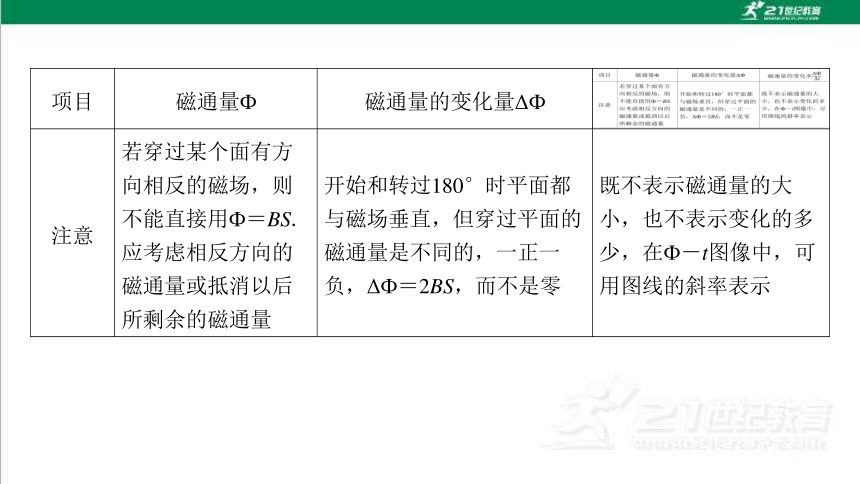
项目 磁通量Ф 磁通量的变化量ΔФ
注意 若穿过某个面有方 向相反的磁场,则 不能直接用Ф=BS. 应考虑相反方向的 磁通量或抵消以后 所剩余的磁通量 开始和转过180°时平面都 与磁场垂直,但穿过平面的磁通量是不同的,一正一负,ΔФ=2BS,而不是零 既不表示磁通量的大 小,也不表示变化的多 少,在Ф-t图像中,可 用图线的斜率表示
研习 经典
A. 感应电动势的大小与线圈的匝数无关
B. 穿过线圈的磁通量越大,感应电动势越大
C. 穿过线圈的磁通量变化越快,感应电动势越大
D. 感应电流产生的磁场方向与原磁场方向始终相同
C
名师点评
这类问题重在培养科学思维,要正确区分磁通量、磁通量的变化量、磁通量的变 化率,知道感应电动势的大小与磁通量的变化率成正比,与磁通量、磁通量的变化量 没有必然联系.
对应 训练
A. 0.30 V B. 0.44 V
C. 0.59 V D. 4.3 V
B
第*页
研习任务二 导线切割磁感线时的感应电动势
合作 讨论
如图所示,把矩形线框CDMN放在磁感应强度为B的匀强磁场里,线框平面跟磁感线 垂直.设线框可动部分导体棒MN的长度为l,它以速度v向右运动,在Δt时间内,由原 来的位置MN移到M1N1.这个过程中回路中产生的感应电动势多大?
提示:这个过程中线框的面积变化量是ΔS=lvΔt
穿过闭合电路的磁通量的变化量是ΔФ=BΔS=BlvΔt
由此求得感应电动势E=Blv.
教材 认知
图1 图2
Blv
Blvsin θ
3. 对公式的理解
(1)l取有效长度
①如图1所示,l是导线切割磁感线的有效长度,即导线两端点连接后在垂直于B、v方 向上的投影长度(图中虚线的长度).
②如图2所示,长为l的导体棒垂直切割磁感线时,其感应电动势E=Blvsin θ≠Blv,导 体棒的有效长度为l'=lsin θ.
③如图3所示,l是接入回路中的长度.
④如图4所示,l是处于磁场中的长度.
图1 图2
图3 图4
①公式中的v应理解为导体和磁场间的相对速度,当导体不动而磁场运动时,也有感 应电动势产生.
②若速度v为平均值,E就为平均感应电动势;若速度v为瞬时值,E就为瞬时感 应电动势.
③v取既垂直于磁场又垂直于导体棒的分速度.
(2)对v的理解
E=Blvsin θ
区别 研究对象 整个闭合回路 回路中做切割磁感线运动的那部分导体
区别 适用范围 各种电磁感应现象 只适用于匀强磁场中导体切割磁感线 运动的情况
计算结果 Δt内的平均感应电动势 某一时刻的瞬时感应电动势
联系
研习 经典
B
对应 训练
A. 杆OP产生的感应电动势恒定
B. 杆OP受到的安培力不变
C. 杆MN做匀加速直线运动
D. 杆MN中的电流逐渐减小
AD
A. φO>φC B. φC>φA
C. φO=φA D. φO-φA=φA-φC
解析:由题图可看出OA导体棒转动切割磁感线,则根据右手定则可知φO>φA,其中 导体棒AC段不在磁场中,不切割磁感线,电流为0,则φC=φA,A正确,B、C错误; 根据以上分析可知φO-φA>0,φA-φC=0,则φO-φA>φA-φC,D错误.故选A.
A
第*页
课时作业(六)
[基础训练]
A B
C D
BCD
解析:由图A所示可知,v与金属导体不垂直,感应电动势E=Blvsin θ,A错误;由图 B所示可知,金属导体垂直切割磁感线,则E=Blv,B正确;由图C所示可知,金属导 体水平部分不切割磁感线,只有竖直部分切割磁感线,感应电动势E=Blv,C正确; 由图D所示可知,金属导体切割磁感线的有效长度为l,感应电动势E=Blv,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 越来越大 B. 越来越小
C. 保持不变 D. 无法判断
C
解析:金属棒ab做平抛运动,其水平方向的分运动是匀速直线运动,水平分速度保持不变,等于v0,由感应电动势公式E=Blvsin α,vsin α是垂直于磁感线方向的分速度,即平抛运动的水平分速度,等于v0,则感应电动势E=Blv0,B、l、v0均不变,则感应电动势大小保持不变.则C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
D
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
BD
A. 导体棒a离开导轨至落地过程中,水平位移大小为0.6 m
B. 导体棒a离开导轨至落地前,其感应电动势不变
C. 导体棒a在导轨上运动的过程中,导体棒b有向右运动的趋势
D. 导体棒a在导轨上运动的过程中,通过电阻R的电荷量为0.58 C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 0.8 V 方向:adcb
B. 0.8 V 方向:abcd
C. 0.4 V 方向:adcb
D. 0.4 V 方向:abcd
C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. N点与M点的磁感应强度大小相等,方向相同
B. 线圈沿PN方向运动时,穿过线圈的磁通量不变
C. 线圈从P点开始竖直向上运动时,线圈中无感应电流
D. 线圈从P到M过程的感应电动势与从P到N过程的感应电动势 相等
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
解析:通电直导线在周围产生的磁场是以导线上各点为圆心的同心圆,MN、长直导 线均与y轴平行,则M点与N点到长直导线的距离相等,故两点的磁感应强度大小相 等,方向相同,A正确;线圈圆心在P点时,穿过线圈向上的磁感线与穿过线圈向下 的磁感线相互抵消,即磁通量为零,又由于离导线越远,磁场越弱,故线圈沿PN方 向运动时,穿过线圈的磁通量先增加后减少,B错误;线圈从P点开始竖直向上运动 时,穿过线圈的磁通量始终为零,由感应电流产生的条件知,线圈中无感应电流,C 正确;线圈从P到M的过程和从P到N的过程,穿过线圈的磁通量的变化量相同,所用 时间不同,故感应电动势不同,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
[能力提升]
A. 在开始的2 s内穿过线圈的磁通量变化率大小等于0.08 Wb/s
B. 在开始的2 s内穿过线圈的磁通量的变化量等于零
C. 在开始的2 s内线圈中产生的感应电动势等于8 V
D. 在第3 s末线圈中的感应电动势等于零
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 电路中的感应电流大小不变
B. 电路中的感应电动势大小不变
C. 电路中的感应电动势逐渐增大
D. 电路中的感应电流减小
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
BC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,一不可伸长的细绳的上端固定,下端系在边长为l=0.40 m的正方形金属框 的一个顶点上.金属框的一条对角线水平,其下方有方向垂直于金属框所在平面的匀 强磁场.已知构成金属框的导线单位长度的阻值为λ=5.0×10-3 Ω/m;在t=0到t=3.0 s时间内,磁感应强度大小随时间t的变化关系为B(t)=0.3-0.1t(SI).求:
(1)t=2.0 s时金属框所受安培力的大小;
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)在t=0到t=2.0 s时间内金属框产生的焦耳热.
答案:(2)0.016 J
解析:(2)0~2.0 s内金属框产生的焦耳热为
Q=I2Rt=12×0.008×2 J=0.016 J.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图所示,两根足够长、电阻不计且相距L=0.2 m的平行金属导轨固定在倾角θ =37°的绝缘斜面上,顶端接有一个额定电压U=4 V的小灯泡,两导轨间有一磁感 应强度大小B=5 T、方向垂直斜面向上的匀强磁场.今将一根长为2L、质量m=0.2 kg、电阻r=1.0 Ω的金属棒垂直于导
轨放置在顶端附近无初速度释放,金属棒与导轨接触良好,金属棒与导轨间的动摩擦 因数μ=0.25,已知金属棒下滑到速度稳定时,小灯泡恰能正常发光,重力加速度取g =10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)金属棒刚开始运动时的加速度大小;
答案:(1)4 m/s2
解析:(1)金属棒刚开始运动时初速度为零,不受安培力作用,由牛顿第二定律得:
mgsin θ-μmgcos θ=ma,代入数据得:a=4 m/s2.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)金属棒稳定下滑时的速度大小.
答案:(2)4.8 m/s
解析:(2)设金属棒稳定下滑时的速度为v,感应电动势为E(金属棒的有效长度为L),回路中的电流为I,由平衡条件得:mgsin θ=BIL+μmgcos θ ①
由法拉第电磁感应定律得E=BLv ③
联立①②③解得:v=4.8 m/s.
1
2
3
4
5
6
7
8
9
10
11
12
13
第二章 电磁感应及其应用
2.法拉第电磁感应定律
第*页
研习任务一 法拉第电磁感应定律
合作 讨论
如图所示,将条形磁铁从同一高度插入线圈中,快速插入和缓慢插入有什么相 同和不同?
提示:同样的磁体、同样的线圈匝数,磁体穿过线圈的过程中线圈磁通量的变化量是相同的,但是磁体穿过的时间不同,从而磁通量的变化快慢不同,即磁通量的变化率不同.
教材 认知
1. 感应电动势
(2)在电磁感应现象中,闭合回路中的感应电流由感应电动势和回路的电阻决定.
电磁感应
电源
感应电动势
变化率
伏
特(V)
项目 磁通量Ф 磁通量的变化量ΔФ
物理
意义 某时刻穿过磁场中某个面的磁感线条数 在某一过程中穿过某个面 的磁通量的变化量 穿过某个面的磁通量变 化的快慢
当B、S互相垂直时大小计算 Ф=BS
项目 磁通量Ф 磁通量的变化量ΔФ
注意 若穿过某个面有方 向相反的磁场,则 不能直接用Ф=BS. 应考虑相反方向的 磁通量或抵消以后 所剩余的磁通量 开始和转过180°时平面都 与磁场垂直,但穿过平面的磁通量是不同的,一正一负,ΔФ=2BS,而不是零 既不表示磁通量的大 小,也不表示变化的多 少,在Ф-t图像中,可 用图线的斜率表示
研习 经典
A. 感应电动势的大小与线圈的匝数无关
B. 穿过线圈的磁通量越大,感应电动势越大
C. 穿过线圈的磁通量变化越快,感应电动势越大
D. 感应电流产生的磁场方向与原磁场方向始终相同
C
名师点评
这类问题重在培养科学思维,要正确区分磁通量、磁通量的变化量、磁通量的变 化率,知道感应电动势的大小与磁通量的变化率成正比,与磁通量、磁通量的变化量 没有必然联系.
对应 训练
A. 0.30 V B. 0.44 V
C. 0.59 V D. 4.3 V
B
第*页
研习任务二 导线切割磁感线时的感应电动势
合作 讨论
如图所示,把矩形线框CDMN放在磁感应强度为B的匀强磁场里,线框平面跟磁感线 垂直.设线框可动部分导体棒MN的长度为l,它以速度v向右运动,在Δt时间内,由原 来的位置MN移到M1N1.这个过程中回路中产生的感应电动势多大?
提示:这个过程中线框的面积变化量是ΔS=lvΔt
穿过闭合电路的磁通量的变化量是ΔФ=BΔS=BlvΔt
由此求得感应电动势E=Blv.
教材 认知
图1 图2
Blv
Blvsin θ
3. 对公式的理解
(1)l取有效长度
①如图1所示,l是导线切割磁感线的有效长度,即导线两端点连接后在垂直于B、v方 向上的投影长度(图中虚线的长度).
②如图2所示,长为l的导体棒垂直切割磁感线时,其感应电动势E=Blvsin θ≠Blv,导 体棒的有效长度为l'=lsin θ.
③如图3所示,l是接入回路中的长度.
④如图4所示,l是处于磁场中的长度.
图1 图2
图3 图4
①公式中的v应理解为导体和磁场间的相对速度,当导体不动而磁场运动时,也有感 应电动势产生.
②若速度v为平均值,E就为平均感应电动势;若速度v为瞬时值,E就为瞬时感 应电动势.
③v取既垂直于磁场又垂直于导体棒的分速度.
(2)对v的理解
E=Blvsin θ
区别 研究对象 整个闭合回路 回路中做切割磁感线运动的那部分导体
区别 适用范围 各种电磁感应现象 只适用于匀强磁场中导体切割磁感线 运动的情况
计算结果 Δt内的平均感应电动势 某一时刻的瞬时感应电动势
联系
研习 经典
B
对应 训练
A. 杆OP产生的感应电动势恒定
B. 杆OP受到的安培力不变
C. 杆MN做匀加速直线运动
D. 杆MN中的电流逐渐减小
AD
A. φO>φC B. φC>φA
C. φO=φA D. φO-φA=φA-φC
解析:由题图可看出OA导体棒转动切割磁感线,则根据右手定则可知φO>φA,其中 导体棒AC段不在磁场中,不切割磁感线,电流为0,则φC=φA,A正确,B、C错误; 根据以上分析可知φO-φA>0,φA-φC=0,则φO-φA>φA-φC,D错误.故选A.
A
第*页
课时作业(六)
[基础训练]
A B
C D
BCD
解析:由图A所示可知,v与金属导体不垂直,感应电动势E=Blvsin θ,A错误;由图 B所示可知,金属导体垂直切割磁感线,则E=Blv,B正确;由图C所示可知,金属导 体水平部分不切割磁感线,只有竖直部分切割磁感线,感应电动势E=Blv,C正确; 由图D所示可知,金属导体切割磁感线的有效长度为l,感应电动势E=Blv,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 越来越大 B. 越来越小
C. 保持不变 D. 无法判断
C
解析:金属棒ab做平抛运动,其水平方向的分运动是匀速直线运动,水平分速度保持不变,等于v0,由感应电动势公式E=Blvsin α,vsin α是垂直于磁感线方向的分速度,即平抛运动的水平分速度,等于v0,则感应电动势E=Blv0,B、l、v0均不变,则感应电动势大小保持不变.则C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
D
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
BD
A. 导体棒a离开导轨至落地过程中,水平位移大小为0.6 m
B. 导体棒a离开导轨至落地前,其感应电动势不变
C. 导体棒a在导轨上运动的过程中,导体棒b有向右运动的趋势
D. 导体棒a在导轨上运动的过程中,通过电阻R的电荷量为0.58 C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 0.8 V 方向:adcb
B. 0.8 V 方向:abcd
C. 0.4 V 方向:adcb
D. 0.4 V 方向:abcd
C
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. N点与M点的磁感应强度大小相等,方向相同
B. 线圈沿PN方向运动时,穿过线圈的磁通量不变
C. 线圈从P点开始竖直向上运动时,线圈中无感应电流
D. 线圈从P到M过程的感应电动势与从P到N过程的感应电动势 相等
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
解析:通电直导线在周围产生的磁场是以导线上各点为圆心的同心圆,MN、长直导 线均与y轴平行,则M点与N点到长直导线的距离相等,故两点的磁感应强度大小相 等,方向相同,A正确;线圈圆心在P点时,穿过线圈向上的磁感线与穿过线圈向下 的磁感线相互抵消,即磁通量为零,又由于离导线越远,磁场越弱,故线圈沿PN方 向运动时,穿过线圈的磁通量先增加后减少,B错误;线圈从P点开始竖直向上运动 时,穿过线圈的磁通量始终为零,由感应电流产生的条件知,线圈中无感应电流,C 正确;线圈从P到M的过程和从P到N的过程,穿过线圈的磁通量的变化量相同,所用 时间不同,故感应电动势不同,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
[能力提升]
A. 在开始的2 s内穿过线圈的磁通量变化率大小等于0.08 Wb/s
B. 在开始的2 s内穿过线圈的磁通量的变化量等于零
C. 在开始的2 s内线圈中产生的感应电动势等于8 V
D. 在第3 s末线圈中的感应电动势等于零
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 电路中的感应电流大小不变
B. 电路中的感应电动势大小不变
C. 电路中的感应电动势逐渐增大
D. 电路中的感应电流减小
AC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
BC
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图,一不可伸长的细绳的上端固定,下端系在边长为l=0.40 m的正方形金属框 的一个顶点上.金属框的一条对角线水平,其下方有方向垂直于金属框所在平面的匀 强磁场.已知构成金属框的导线单位长度的阻值为λ=5.0×10-3 Ω/m;在t=0到t=3.0 s时间内,磁感应强度大小随时间t的变化关系为B(t)=0.3-0.1t(SI).求:
(1)t=2.0 s时金属框所受安培力的大小;
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)在t=0到t=2.0 s时间内金属框产生的焦耳热.
答案:(2)0.016 J
解析:(2)0~2.0 s内金属框产生的焦耳热为
Q=I2Rt=12×0.008×2 J=0.016 J.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. 如图所示,两根足够长、电阻不计且相距L=0.2 m的平行金属导轨固定在倾角θ =37°的绝缘斜面上,顶端接有一个额定电压U=4 V的小灯泡,两导轨间有一磁感 应强度大小B=5 T、方向垂直斜面向上的匀强磁场.今将一根长为2L、质量m=0.2 kg、电阻r=1.0 Ω的金属棒垂直于导
轨放置在顶端附近无初速度释放,金属棒与导轨接触良好,金属棒与导轨间的动摩擦 因数μ=0.25,已知金属棒下滑到速度稳定时,小灯泡恰能正常发光,重力加速度取g =10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)金属棒刚开始运动时的加速度大小;
答案:(1)4 m/s2
解析:(1)金属棒刚开始运动时初速度为零,不受安培力作用,由牛顿第二定律得:
mgsin θ-μmgcos θ=ma,代入数据得:a=4 m/s2.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)金属棒稳定下滑时的速度大小.
答案:(2)4.8 m/s
解析:(2)设金属棒稳定下滑时的速度为v,感应电动势为E(金属棒的有效长度为L),回路中的电流为I,由平衡条件得:mgsin θ=BIL+μmgcos θ ①
由法拉第电磁感应定律得E=BLv ③
联立①②③解得:v=4.8 m/s.
1
2
3
4
5
6
7
8
9
10
11
12
13
同课章节目录
