教科版高中物理选择性必修第二册第一章磁场对电流的作用3洛伦兹力课件(46页ppt)
文档属性
| 名称 | 教科版高中物理选择性必修第二册第一章磁场对电流的作用3洛伦兹力课件(46页ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-15 23:12:24 | ||
图片预览










文档简介
(共46张PPT)
第一章 磁场对电流的作用
3.洛伦兹力
第*页
核心素养:1.通过实验,认识洛伦兹力. 2.能判断洛伦兹力的方向,会计算洛伦兹力 的大小. 3.能用洛伦兹力分析带电粒子在匀强磁场中的圆周运动.
第*页
研习任务一 洛伦兹力及其方向
合作 讨论
如图所示,电子由阴极向阳极运动(向右运动)过程中向下发生了偏转,试问:
(1)什么力使电子偏转?该力的方向如何?
提示:(1)电子在磁场中运动要受到洛伦兹力,是洛伦兹力使电 子运动方向发生偏转,力的方向向下.
(2)电子运动轨迹附近的磁场方向如何?电子所受洛伦兹力与磁场方向、电子运动 方向存在什么关系?
提示:(2)电子运动轨迹附近的磁场方向由N极指向S极,电子所 受洛伦兹力方向与磁场方向以及电子运动方向垂直,我们可以用 左手定则来判断.
教材 认知
1. 初识洛伦兹力
(1)定义: 在磁场中受到的磁场力.
(2)应用:①传统的电视显像管中利用特殊线圈产生的 控制电子偏转、扫 描出画面;②使宇宙射线发生 保护地球.
2. 洛伦兹力方向的判断——左手定则:伸开左手,使拇指与其余四个手指垂直,并 且都与手掌在同一个平面内;让磁感线从掌心垂直进入,并使 指向正电荷运 动的方向,这时拇指所指的方向就是运动的 在磁场中所受洛伦兹力的方 向.负电荷受力的方向与正电荷受力的方向 .
运动电荷
磁场
偏转
四指
正电荷
相反
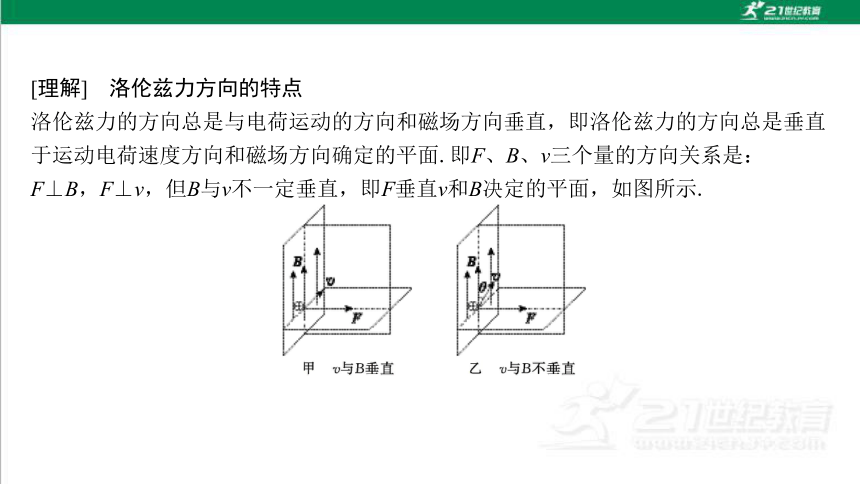
[理解] 洛伦兹力方向的特点
洛伦兹力的方向总是与电荷运动的方向和磁场方向垂直,即洛伦兹力的方向总是垂直 于运动电荷速度方向和磁场方向确定的平面.即F、B、v三个量的方向关系是: F⊥B,F⊥v,但B与v不一定垂直,即F垂直v和B决定的平面,如图所示.
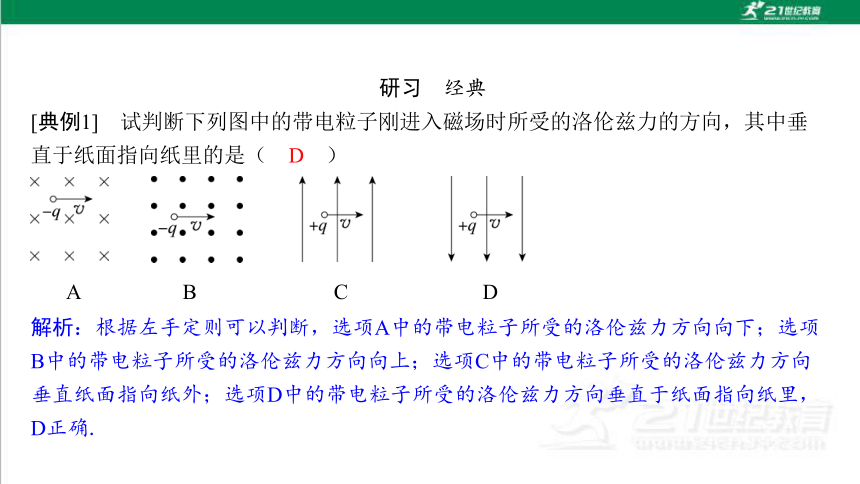
研习 经典
A B
C D
D
解析:根据左手定则可以判断,选项A中的带电粒子所受的洛伦兹力方向向下;选项 B中的带电粒子所受的洛伦兹力方向向上;选项C中的带电粒子所受的洛伦兹力方向 垂直纸面指向纸外;选项D中的带电粒子所受的洛伦兹力方向垂直于纸面指向纸里, D正确.
名师点评
判断运动电荷所受的洛伦兹力方向时使用左手定则.解题时,要明确所带电荷的 电性与四指指向的关系.对于正电荷,四指指向电荷的运动方向;但对于负电荷,四 指应指向电荷运动的反方向.
对应 训练
A. z轴正方向的磁场
B. y轴负方向的磁场
C. x轴正方向的磁场
D. y轴正方向的磁场
解析:电子带负电,且由阴极向阳极运动,受力沿z轴正向,根据左手定则,四指指 向x轴负向,大拇指指向z轴正向,则手心朝向y轴正向,磁场穿过手心,可知需加y轴 负方向的磁场,故B正确.
B
第*页
研习任务二 洛伦兹力的大小
合作 讨论
如图所示,匀强磁场的磁感应强度大小为B. 设磁场中有一段长度为L的通电导线,横 截面积为S,单位体积中含有的自由电荷数为n,每个自由电荷的电荷量为q且定向移 动的速率都是v.
(1)导线中的电流是多大?导线在磁场中所受安培力多大?
提示:(1)根据电流的微观决定式,导线中的电流I=nqSv;由安 培力公式F=BIL,得导线在磁场中所受安培力F安=BLnqSv.
(2)长为L的导线中含有的自由电荷数为多少?每个自由电荷所受洛伦兹力多大?
教材 认知
1. 洛伦兹力的大小:电荷量为q的粒子以速度v运动时,如果速度方向与磁感应强度B 的方向 ,那么粒子受到的洛伦兹力为F= .
2. 一般表达式:电荷运动的方向与磁场的方向夹角为θ 时,电荷所受的洛伦兹力为F = .
3. 当v⊥B,F洛= ,即当电荷的速度方向与磁场方向垂直时,电荷受到的洛伦 兹力最大.
4. 当v∥B,F洛= ,即当电荷的速度方向与磁场方向平行时,电荷所受洛伦兹力 为零.
5. 当v与B成θ角时,F= .
垂直
qvB
qvBsin θ
qvB
0
qvBsin θ
比较项目 洛伦兹力 电场力
性质 磁场对在其中运动电荷的作用力 电场对放入其中的电荷的作用力
产生条件 v≠0且v不与B平行 无条件限制,电场中的电荷一定受到电场 力作用
大小 F=qvB(v⊥B) F=qE
力的方向与场方向的关系 一定是F⊥B,F⊥v 正电荷所受电场力的方向与电场方向相 同,负电荷所受电场力的方向与电场方向 相反
[理解] 洛伦兹力和电场力的比较
比较项目 洛伦兹力 电场力
做功情况 任何情况下都不做功 可能做正功、负功或不做功
力F为零时 场的情况 F为零,B不一定为零 F为零,E一定为零
作用效果 只改变电荷运动的速度方 向,不改变速度大小 既可以改变电荷运动的速度大小,也可以 改变电荷运动的方向
研习 经典
[典例2] 如图所示,各图中的匀强磁场的磁感应强度均为B,带电粒子的速率均 为v,带电荷量均为q.试求出图中带电粒子所受洛伦兹力的大小,并指出洛伦兹 力的方向.
解析:(1)因v⊥B,所以F=qvB,由左手定则可知洛伦兹力方向垂直纸面向外.
(3)由于v与B平行,所以不受洛伦兹力.
(4)v与B垂直,F=qvB,方向垂直v指向左上方.
名师点评
空间思维是解此类题目的关键,学会从不同的角度看v与B的关系,在洛伦兹力的 表达式F=qvBsin θ中,θ是v与B的夹角.我们可以理解为F=qB·vsin θ,其中vsin θ是速 度在垂直磁场方向上的分量;也可以理解为F=qv·Bsin θ,其中Bsin θ是B在垂直v方向 上的分量.所以要理解其物理意义,不要死记硬背.
对应 训练
A. 2∶1 B. 1∶1
C. 1∶2 D. 1∶4
解析:带电粒子的速度方向与磁感线方向垂直时,洛伦兹力F=qvB与电荷量成正 比,与质量无关,C项正确.
C
第*页
研习任务三 带电粒子在匀强磁场中的运动
合作 讨论
如果沿着与磁场垂直的方向发射一束带电粒子(不计重力),这束粒子在匀强磁场中 的运动轨迹会是什么样的呢?
提示:洛伦兹力提供向心力,故只在洛伦兹力的作用下,粒子将做匀速圆周运动,运 动轨迹为圆.
教材 认知
1. 若v∥B,带电粒子(不计重力)所受洛伦兹力F= ,所以粒子在磁场中 做 .
2. 若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向 ,粒子在垂直 于 方向的平面内运动.
(1)洛伦兹力与粒子的运动方向 ,只改变粒子速度的 ,不改变粒 子速度的 .
(2)带电粒子在垂直于磁场的平面内做 运动, 提供 向心力.
0
匀速直线运动
垂直
磁场
垂直
方向
大小
匀速圆周
洛伦兹力
研习 经典
A. 粒子的速率加倍,周期减半
B. 粒子的速率不变,轨道半径减半
D. 粒子的速率不变,周期减半
BD
对应 训练
A. M带负电,N带正电
B. M的速率小于N的速率
C. 洛伦兹力对M、N不做功
D. M的运动时间大于N的运动时间
AC
A. R1∶R2=1∶2
B. R1∶R2=2∶1
C. T1∶T2=1∶1
D. T1∶T2=2∶1
A
第*页
课时作业(三)
[基础训练]
A. 洛伦兹力对运动电荷一定不做功
B. 带电粒子在磁场中运动时,一定受到洛伦兹力作用
C. 正电荷在电场中所受电场力的方向就是电场强度的方向
D. 正电荷在磁场中所受洛伦兹力的方向就是磁感应强度的方向
解析:洛伦兹力与速度方向垂直,则对运动电荷一定不做功,A正确;带电粒子在磁 场中运动时,若速度方向与磁场方向平行,则不受洛伦兹力作用,B错误;正电荷在 电场中所受电场力的方向就是电场强度的方向,C正确;正电荷在磁场中所受洛伦兹 力的方向与磁感应强度的方向垂直,D错误;故选AC.
AC
1
2
3
4
5
6
7
8
9
10
A. F、B、v三者必定均相互垂直
B. F必定垂直于B、v,但B不一定垂直v
C. B必定垂直于F,但F不一定垂直于v
D. v必定垂直于F,但F不一定垂直于B
解析:洛伦兹力垂直于v与B所决定的平面,但v与B不一定要垂直,但v与B不能平行.
B
1
2
3
4
5
6
7
8
9
10
B
1
2
3
4
5
6
7
8
9
10
A. 竖直向下沿直线射向地面
B. 相对于预定地点稍向东偏转
C. 相对于预定地点稍向西偏转
D. 相对于预定地点稍向北偏转
解析:由左手定则判断洛伦兹力方向向东,相对于预定地点稍向东偏转.本题粒子相对于地面竖直向下运动,因此不需要同时考虑地球的自转,故选B.
B
1
2
3
4
5
6
7
8
9
10
D. 若只改变入射速度方向,粒子不可能经过O点
C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
6. 一束电子(电量为e)以速度v0从磁场右边界垂直射入宽为d,磁感应强度为B的匀 强磁场中,如图所示.电子束离开磁场时速度方向与入射速度方向成30°角.(忽略电 子所受重力.e、v0、B、d已知)
(1)求电子在磁场中运动的轨道半径;
答案:2d
1
2
3
4
5
6
7
8
9
10
(2)求电子的质量;
1
2
3
4
5
6
7
8
9
10
(3)求电子在磁场中运动时间.
1
2
3
4
5
6
7
8
9
10
[能力提升]
A. 小物块一定带正电
B. 小物块在斜面上运动时做匀加速直线运动
C. 小物块在斜面上运动时做加速度增大,而速度也增大的变加速直线运动
B
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 导体中电流为I=neSvL
B. 导体中自由电子个数为N=nSL
C. 导体放置在垂直纸面向外、磁感应强度为B的磁场中,导线所受 安培力F安=B(neSv)L
D. 导体放置在垂直纸面向外、磁感应强度为B的磁场中,导线中每 个电子所受洛伦兹力F=evB
BCD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 滑块在a点受重力、支持力和洛伦兹力作用
C. 洛伦兹力做正功
D. 滑块的机械能增大
B
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10. 如图所示,质量m=1×10-4 kg的小球,带有q=5×10-4 C的正电荷,套在一根与 水平方向成θ=37°角的足够长绝缘杆上.小球可以沿杆滑动,与杆间的动摩擦因数μ =0.4,这个装置放在磁感应强度B=0.5 T的匀强磁场中,求小球无初速释放后沿杆 下滑的最大加速度和最大速度(g=10 m/s2).
答案:6 m/s2 9.2 m/s
1
2
3
4
5
6
7
8
9
10
解析:小球无初速释放后,所受洛伦兹力方向垂直杆斜向上,开始阶段小球速度小, 洛伦兹力较小,杆对球的支持力垂直杆斜向上,且逐渐减小,当速度达到某值后,支 持力FN减为零,杆对球的摩擦力也减为零,此时球的加速度最大,根据牛顿第二定律 可得mamax=mgsin θ,解得amax=6 m/s2.
此后杆对球的支持力垂直于杆向下且随速度的增大而增大,当摩擦力Ff=mgsin θ时小 球所受合力为零,达到最大速度,此时根据牛顿第二定律得qvmB=mgcos θ+FN,Ff =mgsin θ,且Ff=μFN,解得vm=9.2 m/s.
1
2
3
4
5
6
7
8
9
10
第一章 磁场对电流的作用
3.洛伦兹力
第*页
核心素养:1.通过实验,认识洛伦兹力. 2.能判断洛伦兹力的方向,会计算洛伦兹力 的大小. 3.能用洛伦兹力分析带电粒子在匀强磁场中的圆周运动.
第*页
研习任务一 洛伦兹力及其方向
合作 讨论
如图所示,电子由阴极向阳极运动(向右运动)过程中向下发生了偏转,试问:
(1)什么力使电子偏转?该力的方向如何?
提示:(1)电子在磁场中运动要受到洛伦兹力,是洛伦兹力使电 子运动方向发生偏转,力的方向向下.
(2)电子运动轨迹附近的磁场方向如何?电子所受洛伦兹力与磁场方向、电子运动 方向存在什么关系?
提示:(2)电子运动轨迹附近的磁场方向由N极指向S极,电子所 受洛伦兹力方向与磁场方向以及电子运动方向垂直,我们可以用 左手定则来判断.
教材 认知
1. 初识洛伦兹力
(1)定义: 在磁场中受到的磁场力.
(2)应用:①传统的电视显像管中利用特殊线圈产生的 控制电子偏转、扫 描出画面;②使宇宙射线发生 保护地球.
2. 洛伦兹力方向的判断——左手定则:伸开左手,使拇指与其余四个手指垂直,并 且都与手掌在同一个平面内;让磁感线从掌心垂直进入,并使 指向正电荷运 动的方向,这时拇指所指的方向就是运动的 在磁场中所受洛伦兹力的方 向.负电荷受力的方向与正电荷受力的方向 .
运动电荷
磁场
偏转
四指
正电荷
相反
[理解] 洛伦兹力方向的特点
洛伦兹力的方向总是与电荷运动的方向和磁场方向垂直,即洛伦兹力的方向总是垂直 于运动电荷速度方向和磁场方向确定的平面.即F、B、v三个量的方向关系是: F⊥B,F⊥v,但B与v不一定垂直,即F垂直v和B决定的平面,如图所示.
研习 经典
A B
C D
D
解析:根据左手定则可以判断,选项A中的带电粒子所受的洛伦兹力方向向下;选项 B中的带电粒子所受的洛伦兹力方向向上;选项C中的带电粒子所受的洛伦兹力方向 垂直纸面指向纸外;选项D中的带电粒子所受的洛伦兹力方向垂直于纸面指向纸里, D正确.
名师点评
判断运动电荷所受的洛伦兹力方向时使用左手定则.解题时,要明确所带电荷的 电性与四指指向的关系.对于正电荷,四指指向电荷的运动方向;但对于负电荷,四 指应指向电荷运动的反方向.
对应 训练
A. z轴正方向的磁场
B. y轴负方向的磁场
C. x轴正方向的磁场
D. y轴正方向的磁场
解析:电子带负电,且由阴极向阳极运动,受力沿z轴正向,根据左手定则,四指指 向x轴负向,大拇指指向z轴正向,则手心朝向y轴正向,磁场穿过手心,可知需加y轴 负方向的磁场,故B正确.
B
第*页
研习任务二 洛伦兹力的大小
合作 讨论
如图所示,匀强磁场的磁感应强度大小为B. 设磁场中有一段长度为L的通电导线,横 截面积为S,单位体积中含有的自由电荷数为n,每个自由电荷的电荷量为q且定向移 动的速率都是v.
(1)导线中的电流是多大?导线在磁场中所受安培力多大?
提示:(1)根据电流的微观决定式,导线中的电流I=nqSv;由安 培力公式F=BIL,得导线在磁场中所受安培力F安=BLnqSv.
(2)长为L的导线中含有的自由电荷数为多少?每个自由电荷所受洛伦兹力多大?
教材 认知
1. 洛伦兹力的大小:电荷量为q的粒子以速度v运动时,如果速度方向与磁感应强度B 的方向 ,那么粒子受到的洛伦兹力为F= .
2. 一般表达式:电荷运动的方向与磁场的方向夹角为θ 时,电荷所受的洛伦兹力为F = .
3. 当v⊥B,F洛= ,即当电荷的速度方向与磁场方向垂直时,电荷受到的洛伦 兹力最大.
4. 当v∥B,F洛= ,即当电荷的速度方向与磁场方向平行时,电荷所受洛伦兹力 为零.
5. 当v与B成θ角时,F= .
垂直
qvB
qvBsin θ
qvB
0
qvBsin θ
比较项目 洛伦兹力 电场力
性质 磁场对在其中运动电荷的作用力 电场对放入其中的电荷的作用力
产生条件 v≠0且v不与B平行 无条件限制,电场中的电荷一定受到电场 力作用
大小 F=qvB(v⊥B) F=qE
力的方向与场方向的关系 一定是F⊥B,F⊥v 正电荷所受电场力的方向与电场方向相 同,负电荷所受电场力的方向与电场方向 相反
[理解] 洛伦兹力和电场力的比较
比较项目 洛伦兹力 电场力
做功情况 任何情况下都不做功 可能做正功、负功或不做功
力F为零时 场的情况 F为零,B不一定为零 F为零,E一定为零
作用效果 只改变电荷运动的速度方 向,不改变速度大小 既可以改变电荷运动的速度大小,也可以 改变电荷运动的方向
研习 经典
[典例2] 如图所示,各图中的匀强磁场的磁感应强度均为B,带电粒子的速率均 为v,带电荷量均为q.试求出图中带电粒子所受洛伦兹力的大小,并指出洛伦兹 力的方向.
解析:(1)因v⊥B,所以F=qvB,由左手定则可知洛伦兹力方向垂直纸面向外.
(3)由于v与B平行,所以不受洛伦兹力.
(4)v与B垂直,F=qvB,方向垂直v指向左上方.
名师点评
空间思维是解此类题目的关键,学会从不同的角度看v与B的关系,在洛伦兹力的 表达式F=qvBsin θ中,θ是v与B的夹角.我们可以理解为F=qB·vsin θ,其中vsin θ是速 度在垂直磁场方向上的分量;也可以理解为F=qv·Bsin θ,其中Bsin θ是B在垂直v方向 上的分量.所以要理解其物理意义,不要死记硬背.
对应 训练
A. 2∶1 B. 1∶1
C. 1∶2 D. 1∶4
解析:带电粒子的速度方向与磁感线方向垂直时,洛伦兹力F=qvB与电荷量成正 比,与质量无关,C项正确.
C
第*页
研习任务三 带电粒子在匀强磁场中的运动
合作 讨论
如果沿着与磁场垂直的方向发射一束带电粒子(不计重力),这束粒子在匀强磁场中 的运动轨迹会是什么样的呢?
提示:洛伦兹力提供向心力,故只在洛伦兹力的作用下,粒子将做匀速圆周运动,运 动轨迹为圆.
教材 认知
1. 若v∥B,带电粒子(不计重力)所受洛伦兹力F= ,所以粒子在磁场中 做 .
2. 若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向 ,粒子在垂直 于 方向的平面内运动.
(1)洛伦兹力与粒子的运动方向 ,只改变粒子速度的 ,不改变粒 子速度的 .
(2)带电粒子在垂直于磁场的平面内做 运动, 提供 向心力.
0
匀速直线运动
垂直
磁场
垂直
方向
大小
匀速圆周
洛伦兹力
研习 经典
A. 粒子的速率加倍,周期减半
B. 粒子的速率不变,轨道半径减半
D. 粒子的速率不变,周期减半
BD
对应 训练
A. M带负电,N带正电
B. M的速率小于N的速率
C. 洛伦兹力对M、N不做功
D. M的运动时间大于N的运动时间
AC
A. R1∶R2=1∶2
B. R1∶R2=2∶1
C. T1∶T2=1∶1
D. T1∶T2=2∶1
A
第*页
课时作业(三)
[基础训练]
A. 洛伦兹力对运动电荷一定不做功
B. 带电粒子在磁场中运动时,一定受到洛伦兹力作用
C. 正电荷在电场中所受电场力的方向就是电场强度的方向
D. 正电荷在磁场中所受洛伦兹力的方向就是磁感应强度的方向
解析:洛伦兹力与速度方向垂直,则对运动电荷一定不做功,A正确;带电粒子在磁 场中运动时,若速度方向与磁场方向平行,则不受洛伦兹力作用,B错误;正电荷在 电场中所受电场力的方向就是电场强度的方向,C正确;正电荷在磁场中所受洛伦兹 力的方向与磁感应强度的方向垂直,D错误;故选AC.
AC
1
2
3
4
5
6
7
8
9
10
A. F、B、v三者必定均相互垂直
B. F必定垂直于B、v,但B不一定垂直v
C. B必定垂直于F,但F不一定垂直于v
D. v必定垂直于F,但F不一定垂直于B
解析:洛伦兹力垂直于v与B所决定的平面,但v与B不一定要垂直,但v与B不能平行.
B
1
2
3
4
5
6
7
8
9
10
B
1
2
3
4
5
6
7
8
9
10
A. 竖直向下沿直线射向地面
B. 相对于预定地点稍向东偏转
C. 相对于预定地点稍向西偏转
D. 相对于预定地点稍向北偏转
解析:由左手定则判断洛伦兹力方向向东,相对于预定地点稍向东偏转.本题粒子相对于地面竖直向下运动,因此不需要同时考虑地球的自转,故选B.
B
1
2
3
4
5
6
7
8
9
10
D. 若只改变入射速度方向,粒子不可能经过O点
C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
6. 一束电子(电量为e)以速度v0从磁场右边界垂直射入宽为d,磁感应强度为B的匀 强磁场中,如图所示.电子束离开磁场时速度方向与入射速度方向成30°角.(忽略电 子所受重力.e、v0、B、d已知)
(1)求电子在磁场中运动的轨道半径;
答案:2d
1
2
3
4
5
6
7
8
9
10
(2)求电子的质量;
1
2
3
4
5
6
7
8
9
10
(3)求电子在磁场中运动时间.
1
2
3
4
5
6
7
8
9
10
[能力提升]
A. 小物块一定带正电
B. 小物块在斜面上运动时做匀加速直线运动
C. 小物块在斜面上运动时做加速度增大,而速度也增大的变加速直线运动
B
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 导体中电流为I=neSvL
B. 导体中自由电子个数为N=nSL
C. 导体放置在垂直纸面向外、磁感应强度为B的磁场中,导线所受 安培力F安=B(neSv)L
D. 导体放置在垂直纸面向外、磁感应强度为B的磁场中,导线中每 个电子所受洛伦兹力F=evB
BCD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 滑块在a点受重力、支持力和洛伦兹力作用
C. 洛伦兹力做正功
D. 滑块的机械能增大
B
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10. 如图所示,质量m=1×10-4 kg的小球,带有q=5×10-4 C的正电荷,套在一根与 水平方向成θ=37°角的足够长绝缘杆上.小球可以沿杆滑动,与杆间的动摩擦因数μ =0.4,这个装置放在磁感应强度B=0.5 T的匀强磁场中,求小球无初速释放后沿杆 下滑的最大加速度和最大速度(g=10 m/s2).
答案:6 m/s2 9.2 m/s
1
2
3
4
5
6
7
8
9
10
解析:小球无初速释放后,所受洛伦兹力方向垂直杆斜向上,开始阶段小球速度小, 洛伦兹力较小,杆对球的支持力垂直杆斜向上,且逐渐减小,当速度达到某值后,支 持力FN减为零,杆对球的摩擦力也减为零,此时球的加速度最大,根据牛顿第二定律 可得mamax=mgsin θ,解得amax=6 m/s2.
此后杆对球的支持力垂直于杆向下且随速度的增大而增大,当摩擦力Ff=mgsin θ时小 球所受合力为零,达到最大速度,此时根据牛顿第二定律得qvmB=mgcos θ+FN,Ff =mgsin θ,且Ff=μFN,解得vm=9.2 m/s.
1
2
3
4
5
6
7
8
9
10
同课章节目录
