10.1.1 对顶角及其性质 课件(共12张PPT) 2024--2025学年沪科版七年级数学下册
文档属性
| 名称 | 10.1.1 对顶角及其性质 课件(共12张PPT) 2024--2025学年沪科版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-15 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
第10章 相交线、平行线与平移
沪科版(2024)七年级下册
第1课时 相交线
情境导入
情境导入
探究新知
观察剪刀剪纸的过程,你有什么发现?
握紧把手时,随着两个把手之间的角逐渐变小,剪刀两刃之间的角也相应变小直到剪开纸片
这两个角之间有什么样的位置关系呢?
探究新知
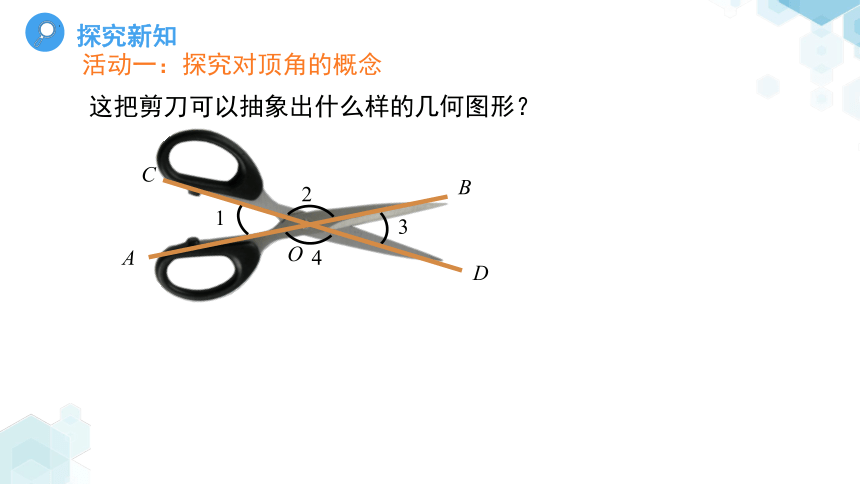
这把剪刀可以抽象出什么样的几何图形?
1
2
3
4
A
B
C
D
O
活动一:探究对顶角的概念
探究新知
1
2
3
4
A
B
C
D
O
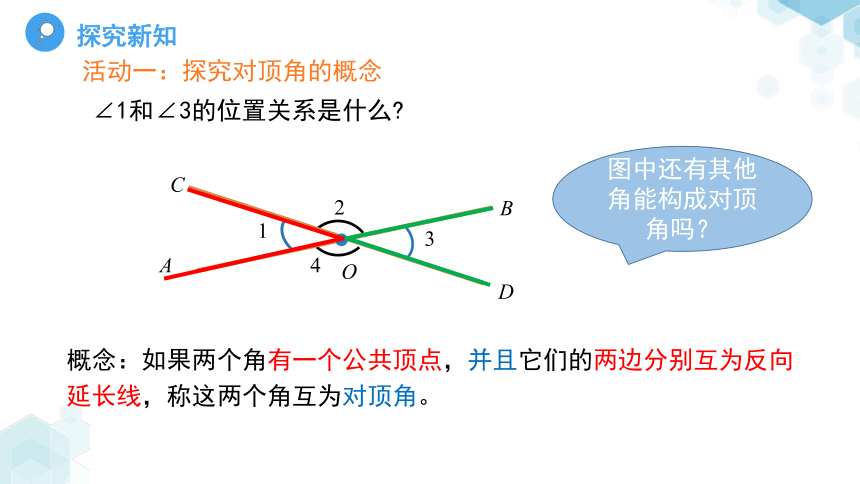
概念:如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,称这两个角互为对顶角。
活动一:探究对顶角的概念
∠1和∠3的位置关系是什么
图中还有其他角能构成对顶角吗?
应用新知
1.在下列各图中,∠1和∠2是不是对顶角?并说明理由
解:(1)不是;∠1和∠2的两边不是互为反向延长线;
(2)不是;∠1和∠2没有公共顶点;
(4)是;∠1和∠2有公共顶点,且两边互为反向延长线.
(3)不是;∠1和∠2没有公共顶点;
探究新知
1
2
3
4
A
B
C
D
O
对顶角的性质:对顶角相等.
∠2=∠4
用量角器量一量
活动二:探究对顶角的性质
∠1与∠2的大小有什么关系?
∠2与∠4呢?
应用新知
2:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数
解:因为∠1和∠2互为邻补角,
所以∠2=180° ∠1=180° 40°=140°
因为∠3与∠1、∠4与∠2互为对顶角
所以∠3=∠1=40°,∠4=∠2=140°
所以∠2=140°,∠3=40°,∠4=140°
课堂检测
解:因为∠AOC:∠BOC=2:7,且互为邻补角
所以设∠AOC=2x°,∠BOC=7x°
则2x+7x=180
解得x=20.
所以∠BOC=140°,
所以∠AOD=140°(对顶角相等)
限时训练
1. 如图,直线AB,CD相交于点O,∠AOC:∠BOC=2:7,则∠BOC= °,∠AOD= °.
代数方法解决几何问题
总结归纳
两条直线相交 分类 位置关系 数量关系 名称
∠1与∠3 ∠2与∠4 ①有公共顶点 ②两边互为反向延长线 相等 对顶角
∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ①有公共顶点 ②有一条公共边 ③另一边互为反向延长线 互补 邻补角
1.必做题:课本 P129 第 1、2;
2.选做题:
思考题:三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角
n条直线相交于一点,有几对对顶角?
作业布置
第10章 相交线、平行线与平移
沪科版(2024)七年级下册
第1课时 相交线
情境导入
情境导入
探究新知
观察剪刀剪纸的过程,你有什么发现?
握紧把手时,随着两个把手之间的角逐渐变小,剪刀两刃之间的角也相应变小直到剪开纸片
这两个角之间有什么样的位置关系呢?
探究新知
这把剪刀可以抽象出什么样的几何图形?
1
2
3
4
A
B
C
D
O
活动一:探究对顶角的概念
探究新知
1
2
3
4
A
B
C
D
O
概念:如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,称这两个角互为对顶角。
活动一:探究对顶角的概念
∠1和∠3的位置关系是什么
图中还有其他角能构成对顶角吗?
应用新知
1.在下列各图中,∠1和∠2是不是对顶角?并说明理由
解:(1)不是;∠1和∠2的两边不是互为反向延长线;
(2)不是;∠1和∠2没有公共顶点;
(4)是;∠1和∠2有公共顶点,且两边互为反向延长线.
(3)不是;∠1和∠2没有公共顶点;
探究新知
1
2
3
4
A
B
C
D
O
对顶角的性质:对顶角相等.
∠2=∠4
用量角器量一量
活动二:探究对顶角的性质
∠1与∠2的大小有什么关系?
∠2与∠4呢?
应用新知
2:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数
解:因为∠1和∠2互为邻补角,
所以∠2=180° ∠1=180° 40°=140°
因为∠3与∠1、∠4与∠2互为对顶角
所以∠3=∠1=40°,∠4=∠2=140°
所以∠2=140°,∠3=40°,∠4=140°
课堂检测
解:因为∠AOC:∠BOC=2:7,且互为邻补角
所以设∠AOC=2x°,∠BOC=7x°
则2x+7x=180
解得x=20.
所以∠BOC=140°,
所以∠AOD=140°(对顶角相等)
限时训练
1. 如图,直线AB,CD相交于点O,∠AOC:∠BOC=2:7,则∠BOC= °,∠AOD= °.
代数方法解决几何问题
总结归纳
两条直线相交 分类 位置关系 数量关系 名称
∠1与∠3 ∠2与∠4 ①有公共顶点 ②两边互为反向延长线 相等 对顶角
∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 ①有公共顶点 ②有一条公共边 ③另一边互为反向延长线 互补 邻补角
1.必做题:课本 P129 第 1、2;
2.选做题:
思考题:三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角
n条直线相交于一点,有几对对顶角?
作业布置
