平均数的再认识 课件(共17张PPT)2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 平均数的再认识 课件(共17张PPT)2024-2025学年五年级下册数学北师大版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-15 06:05:25 | ||
图片预览






文档简介
(共17张PPT)
数据的表示和分析
平均数的再认识
北师大版五年级下册第八单元
体会平均数具有代表性
从2022年9月1日起,武汉市把儿童乘坐城市公共交通工具的免费线从1.2米调整到1.3米。
(1)对这个规定你有什么疑问?
为什么要把免费线调整到1.3米?
探索新知
现在生活条件好了,儿童的身高也高了。
被调查的儿童的平均身高可能高了。
(2)据调查,武汉市某校6岁男童的身高平均值为126.5厘米,女童的身高平均值为124.0厘米。
请同学们读一读调查结果,并根据上面信息解释免票线的合理性。
探索新知
根据武汉市某校6岁儿童的平均身高的得出的数据,儿童的身高变高了;126.5厘米和124.0厘米都是大于1.2米,且接近1.3米,所以要将免费线调整到1.3米。
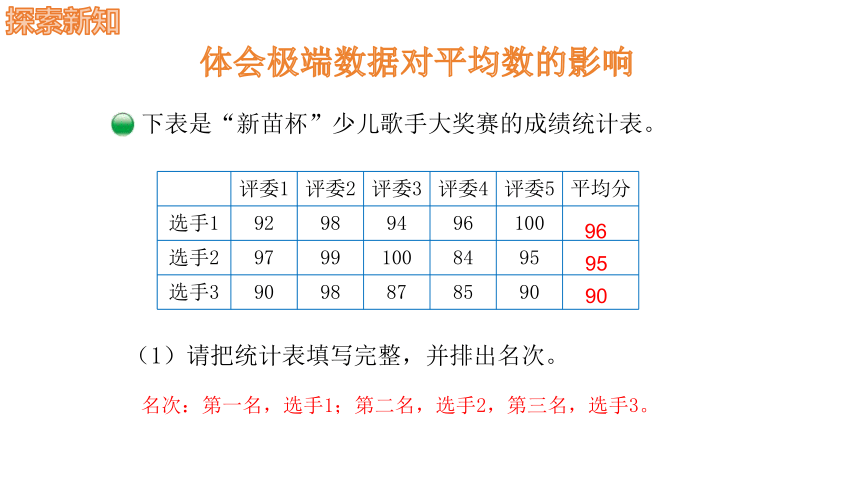
下表是“新苗杯”少儿歌手大奖赛的成绩统计表。
(1)请把统计表填写完整,并排出名次。
评委1 评委2 评委3 评委4 评委5 平均分
选手1 92 98 94 96 100
选手2 97 99 100 84 95
选手3 90 98 87 85 90
96
95
90
名次:第一名,选手1;第二名,选手2,第三名,选手3。
体会极端数据对平均数的影响
探索新知
(2)在实际比赛中,通常都采取去掉一个最高分和一个最低分、然后再计算平均数的计分方法,你能说出 其中的道理吗?
4. 学生展示,交流。
1. 说一说为什么要去掉一个最高分和最低分?
2. 独立计算,求出平均数,并进行排名。
3. 讨论为什么两次计算结果不同,名次也不同?
探索新知
(2)在实际比赛中,通常都采取去掉一个最高分和一个最低分、然后再计算平均数的计分方法,你能说出 其中的道理吗?
4. 学生展示,交流。
1. 说一说为什么要去掉一个最高分和最低分?
2. 独立计算,求出平均数,并进行排名。
3. 讨论为什么两次计算结果不同,名次也不同?
探索新知
(1) 说一说为什么要去掉一个最高分和最低分?
有的评委打分太高或太低。
去掉后,计算的分数会更公平。
去掉后再求平均就更有代表性了。
探索新知
(2)独立计算,求出平均数,并进行排名。
名次:第一名,选手2;第二名,选手1,第三名,选手3。
评委1 评委2 评委3 评委4 评委5 平均分
选手1 92 98 94 96 100
选手2 97 99 100 84 95
选手3 90 98 87 85 90
最终
96
95
90
96
97
89
①
②
③
①
②
③
探索新知
(3)讨论为什么两次计算结果不同,名次也不同?
探索新知
选手2中有较小的数据,现在将较小的数据去掉后,平均分就有了变化,所以选手2的名次就改变了。
像这样在每组数据中出现的较大或较小的数据就是极端数据。
任何一个数有变化,平均数都有反应,所以平均数很灵敏
说一说,你对平均数有了哪些新的认识?
探索新知
随堂小测
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是他们展开了调查。下面是他们调查时使用的评分标准。
巩固练习
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
对于这个组的学生,数学更受欢迎。
(1)分别计算数学和英语喜欢程度的平均分。
数学喜欢程度的平均分是3分,英语喜欢程度的平均分是2.4分。
巩固练习
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(1)计算这些小朋友的平均年龄。
(2)这时,老师也加入做游戏的队伍。他的年龄是45岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(1)这些小朋友的平均年龄为7.875岁。
(2)老师加入后,做游戏的人的平均年龄为12岁。
巩固练习
3.五个数的平均数是28,如果把其中的一个数改成23,这时五个数的平均数是26,这个被改动的数是多少?
改动前五个数的总和是:28×5=140
改动后五个数的总和是:26×5=130
两次相差:140-130=10
被改动的数为:10+23=33
巩固练习
方法一:
方法二:
两次平均数相差:28-26=2
课堂小结
谈谈你对本节课有哪些收获?
平均数具有代表性;受偏大或偏小数据的影响;很灵敏
数据的表示和分析
平均数的再认识
北师大版五年级下册第八单元
体会平均数具有代表性
从2022年9月1日起,武汉市把儿童乘坐城市公共交通工具的免费线从1.2米调整到1.3米。
(1)对这个规定你有什么疑问?
为什么要把免费线调整到1.3米?
探索新知
现在生活条件好了,儿童的身高也高了。
被调查的儿童的平均身高可能高了。
(2)据调查,武汉市某校6岁男童的身高平均值为126.5厘米,女童的身高平均值为124.0厘米。
请同学们读一读调查结果,并根据上面信息解释免票线的合理性。
探索新知
根据武汉市某校6岁儿童的平均身高的得出的数据,儿童的身高变高了;126.5厘米和124.0厘米都是大于1.2米,且接近1.3米,所以要将免费线调整到1.3米。
下表是“新苗杯”少儿歌手大奖赛的成绩统计表。
(1)请把统计表填写完整,并排出名次。
评委1 评委2 评委3 评委4 评委5 平均分
选手1 92 98 94 96 100
选手2 97 99 100 84 95
选手3 90 98 87 85 90
96
95
90
名次:第一名,选手1;第二名,选手2,第三名,选手3。
体会极端数据对平均数的影响
探索新知
(2)在实际比赛中,通常都采取去掉一个最高分和一个最低分、然后再计算平均数的计分方法,你能说出 其中的道理吗?
4. 学生展示,交流。
1. 说一说为什么要去掉一个最高分和最低分?
2. 独立计算,求出平均数,并进行排名。
3. 讨论为什么两次计算结果不同,名次也不同?
探索新知
(2)在实际比赛中,通常都采取去掉一个最高分和一个最低分、然后再计算平均数的计分方法,你能说出 其中的道理吗?
4. 学生展示,交流。
1. 说一说为什么要去掉一个最高分和最低分?
2. 独立计算,求出平均数,并进行排名。
3. 讨论为什么两次计算结果不同,名次也不同?
探索新知
(1) 说一说为什么要去掉一个最高分和最低分?
有的评委打分太高或太低。
去掉后,计算的分数会更公平。
去掉后再求平均就更有代表性了。
探索新知
(2)独立计算,求出平均数,并进行排名。
名次:第一名,选手2;第二名,选手1,第三名,选手3。
评委1 评委2 评委3 评委4 评委5 平均分
选手1 92 98 94 96 100
选手2 97 99 100 84 95
选手3 90 98 87 85 90
最终
96
95
90
96
97
89
①
②
③
①
②
③
探索新知
(3)讨论为什么两次计算结果不同,名次也不同?
探索新知
选手2中有较小的数据,现在将较小的数据去掉后,平均分就有了变化,所以选手2的名次就改变了。
像这样在每组数据中出现的较大或较小的数据就是极端数据。
任何一个数有变化,平均数都有反应,所以平均数很灵敏
说一说,你对平均数有了哪些新的认识?
探索新知
随堂小测
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是他们展开了调查。下面是他们调查时使用的评分标准。
巩固练习
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
对于这个组的学生,数学更受欢迎。
(1)分别计算数学和英语喜欢程度的平均分。
数学喜欢程度的平均分是3分,英语喜欢程度的平均分是2.4分。
巩固练习
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(1)计算这些小朋友的平均年龄。
(2)这时,老师也加入做游戏的队伍。他的年龄是45岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(1)这些小朋友的平均年龄为7.875岁。
(2)老师加入后,做游戏的人的平均年龄为12岁。
巩固练习
3.五个数的平均数是28,如果把其中的一个数改成23,这时五个数的平均数是26,这个被改动的数是多少?
改动前五个数的总和是:28×5=140
改动后五个数的总和是:26×5=130
两次相差:140-130=10
被改动的数为:10+23=33
巩固练习
方法一:
方法二:
两次平均数相差:28-26=2
课堂小结
谈谈你对本节课有哪些收获?
平均数具有代表性;受偏大或偏小数据的影响;很灵敏
