小升初复习精讲精练二《小数、分数、百分数》--北师大版(复习课件)
文档属性
| 名称 | 小升初复习精讲精练二《小数、分数、百分数》--北师大版(复习课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-15 15:51:56 | ||
图片预览











文档简介
第二课时
分数、小数、百分数
(北师大)六年级
下
01
学习目标
内容总览
02
知识梳理
03
典例
04
变式练习
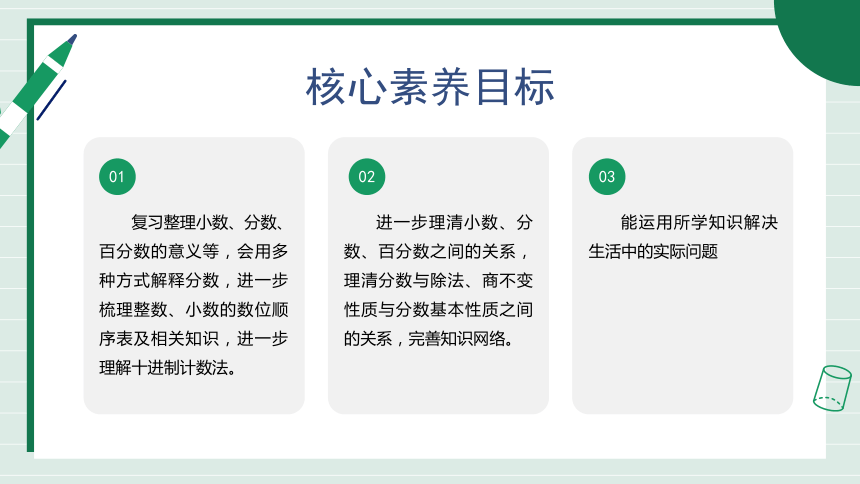
核心素养目标
复习整理小数、分数、百分数的意义等,会用多种方式解释分数,进一步梳理整数、小数的数位顺序表及相关知识,进一步理解十进制计数法。
01
02
进一步理清小数、分数、百分数之间的关系,理清分数与除法、商不变性质与分数基本性质之间的关系,完善知识网络。
03
能运用所学知识解决生活中的实际问题
知识梳理
考点一:分数的意义和分数单位
单位“1”:一个物体,一个计量单位或是许多物体组成的一个整体,
都可以用自然数1来表示,通常我们把它叫作单位“1”。
分 数:把单位“1”平均分成若干份,表示这样的一份或者几份的数,
叫作分数。
分数单位:把单位“1”平均分成若干份,表示其中的一份的数。
分数各部分的名称:
7
4
分数线
分子
分母
(表示平均分的份数)
(表示所取的份数)
知识梳理
考点二:分数的分类
真分数:分子比分母小的分数。
假分数:分子比分母大或者分子和分母相等的分数。
真分数<1
假分数≥1
考点三:分数的基本性质
分数的分子和分母同时乘以或者除以相同的数(零除外),分数的大小不变。
例:一个分数的分母不变,分子乘3,则这个分数( ),
如果分子不变,分母除以5,则这个分数( )。
乘3
乘5
知识梳理
考点四:分数大小的比较
分母相同的两个分数,分子大的分数比较大。
分子相同的两个分数,分母小的分数比较大。
通分:先求出原来几个分母的最小公倍数,然后把各个分数分别化成用这个最小公倍数作分母的分数。
815
?
715
?
>
911
?
1011
?
<
49
?
47
?
<
1112
?
1115
?
>
16
?
49
?
<
16
?
=
1×96×9
?
=
954
?
49
?
=
4×69×6
?
=
2454
?
知识梳理
考点五:最简分数
分子分母是互质数的分数叫最简分数。计算结果,能约分的
要约成最简分数;假分数一般要化成带分数或整数。
判断一个分数能不能化成有限小数的方法:
(1)先把这个分数化成最简分数;
(2)再看这个最简分数的分母是否只含有2和5两个质因数。
425
?
720
?
238
?
714
?
912
?
618
?
√
×
√
√
√
√
知识梳理
考点六:小数的意义
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
如 记作:0.1 记作: 0.08
1
10
8
100
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示。
小数部分的最大计数单位是十分之一,没有最小的计数单位。
小数部分有几个数位,就叫作几位小数。
知识梳理
考点七:小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字。
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
小数的末尾添上0或者去掉0,小数的大小不变。
运用小数的性质,可以在小数末尾添上0。
3.5=3.50
也可以把小数化简。 3.500=3.5
考点八:小数的性质
知识梳理
考点九:求小数的近似数
根据要求,要把小数保留到哪一位,就把这一位后面的尾数按照“四舍五入”法省略,中间用“≈”连接。
精确到十分位就是保留一位小数;
精确到百分位就是保留两位小数;
精确到千分位就是保留三位小数……
5.62975精确到十分位约:( )
5.62975精确到千分位约:( )
5.6
5.630
知识梳理
考点十:循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫作循环小数。如 0.5555…… 8.23838……
0.5555…… 记作:0.5 8.23838……记作:8.238
. .
.
按小数位数是有限还是无限分
小数
有限小数
无限小数
无限循环小数
无限不循环小数
纯循环小数
混循环小数
按小数的整数部分是否为0分
小数
纯小数
带小数(混小数)
考点十一:小数的分类
知识梳理
考点十二:百分数的意义
表示一个数是另一个数的百分之几的数叫百分数。百分数又叫百分率或百分比。
百分数后面不能带单位名称。
(百分数表示两个数的关系,不能带单位名称)
(百分数是一种特殊的分数)
(百分号用“%”表示)
知识梳理
考点十二:小数、分数、百分数之间的关系
小数:实际上是十进分数。
分数:既可以带单位表示一个具体的量,也可以表示两个量的倍数关系。
百分数:表示一个量是另一个量的百分之几,百分数不能带单位,不表示具体的量。
三者之间可以互化:0.25 = 14 = 25%
?
知识梳理
考点十三:分数与除法的关系
被除数÷除数=
被除数
除数
(除数≠0)
a÷b=
a
b
(b≠0)
表示:把单位“1”平均分成9份,取其中的5份。
米表示:把5米平均分成9份,每份是它的( ),
每份是( )米。
19
?
59
?
59
?
59
?
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
把3个苹果平均分成4份,求每份有多少个苹果,用除法计算:3÷4= (个),每份是 个苹果。这里的 表示具体的数量。
3
4
3
4
3
4
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
把一个圆平均分成4份,其中的3份用分数表示是 。
3
4
把一个正方形平均分成4份,涂色部分占其中的一份,用分数表示是 ,3个 用 ×3= 。
1
4
3
4
1
4
1
4
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
红色彩带的长度是绿色彩带长度的 。
3
4
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
(2)分数、除法之间的关系。
(3)商不变的规律与分数基本性质的关系。
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
小数的意义:小数实际是十进制分数的另一种形式,十分之一、百分之一、千分之一……的分数都可以用小数表示,如:0.1、0.01、0.001……。
分数的意义:把单位“1” 平均分成若干份,表示这样的一份或几份的数叫作分数。
百分数的意义:表示一个数是另一个数的百分之几的数叫作百分数。
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
小数、分数、百分数之间可以进行互化。
典例
2.结合具体的例子说一说。
(2)分数、除法之间的关系。
a÷b=???????? (b不为“0”),除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母。
?
典例
2.结合具体的例子说一说。
(3)商不变的规律与分数基本性质的关系。
商不变的规律:被除数和除数同时乘或除以相同的数(0除
外),商不变。
例如:8÷10=0.8;(8×2)÷(10×2)=0.8;
(8÷2)÷(10÷2)=0.8
分数的基本性质:分子与分母同时乘或除以相同的数(0除
外),分数的大小不变。
典例
3.想一想,填一填。
整数部分
小
数
点
小 数 部 分
···
亿 级
万 级
个 级
数位
···
千
亿
位
百
亿
位
十
亿
位
亿
位
千
万
位
百
万
位
十
万
位
万
位
千
位
百
位
十
位
个
位
·
十
分
位
百
分
位
千
分
位
万
分
位
···
计数单位
···
千
亿
百
亿
十
亿
亿
千
万
百
万
十
万
万
千
百
十
个
·
十
分
之
一
百
分
之
一
千
分
之
一
万
分
之
一
···
典例
整数和小数相邻计数单位间的进率都是( )。
10
整数部分
小
数
点
小 数 部 分
···
亿 级
万 级
个 级
数位
···
千
亿
位
百
亿
位
十
亿
位
亿
位
千
万
位
百
万
位
十
万
位
万
位
千
位
百
位
十
位
个
位
·
十
分
位
百
分
位
千
分
位
万
分
位
···
计数单位
···
千
亿
百
亿
十
亿
亿
千
万
百
万
十
万
万
千
百
十
个
·
十
分
之
一
百
分
之
一
千
分
之
一
万
分
之
一
···
变式练习
1.读一读。
从资料中你了解到什么?
你能解释一下这些数据的
具体意义吗?
变式练习
阳光小学六年级一班在调查了全班同学中近视和不近视的人数后,得到如下结果。
近视的
不近视的
占全班人数的几分之几
先把分数改写成小数,再改写成百分数。
说说你是怎样用百分数来表示上面分数的?
=0.6
=60%
≈ 0.286
=28.6%
2.从报刊中找一些分数、小数和百分数,并说一说这些数表示的具体意义。
变式练习
3.用分数表示图形中不同颜色的部分占整个图形的几分之几。
红色占_____
白色占_____
红色占_____
白色占_____
红色占_____
白色占_____
红色占_____
白色占_____
25
?
25
?
12
?
12
?
38
?
58
?
23
?
13
?
变式练习
4.在图中用阴影表示各数。
变式练习
5.在 里填上“>”“<”或“=”。
0.33
67%
25%
125%
0.78
0.8
>
>
=
>
=
<
=
=
课堂总结
今天你有什么收获?
培优拓展
1.甲数比乙数多 10.8,甲数的小数点向左移动一位就正好与乙数相等。甲乙两数分别是多少?
乙数:10.8:(10-1)=1.2
甲数:10.8+1.2=12
答:甲数是 12,乙数是1.2。
培优拓展
2.最简分数????????满足17?
a
b
因为 满足 < < ,7和6之间没有整数,
所以把 和 各自乘2
1
7
a
b
1
6
1
7
1
6
得到 < <
2
14
a
b
1
12
当 = 时不等式成立,且此时母最小,所以a+b=2+13=15。
2
13
a
b
强化练习
1.填空。
(1)( ): ( )= 0.375 = = ( )÷ 40 =( )%。
(2)134>( )> 72% 2611<( )< 360%
(3)养鸡场母鸡的只数占75%,公鸡的只数占25%。
a.母鸡的只数与鸡的总只数的比是( )。
b.公鸡的只数与鸡的总只数的比是( )。
?
3:4
1:4
375
1000
24
15
37.5
1
3
强化练习
2.判断。
(1)58吨 = 62.5%吨 ( )
(2)百分数的意义和分数完全相同。 ( )
(3)王叔叔今年纯收入相当于去年的110%,说明他家今年收入比去年高。 ( )
(4)六(1)班男同学占全班人数的60%,那么女同学占全班人数的40%。 ( )
?
x
x
√
√
强化练习
3.在图中用阴影表示各数。
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
分数、小数、百分数
(北师大)六年级
下
01
学习目标
内容总览
02
知识梳理
03
典例
04
变式练习
核心素养目标
复习整理小数、分数、百分数的意义等,会用多种方式解释分数,进一步梳理整数、小数的数位顺序表及相关知识,进一步理解十进制计数法。
01
02
进一步理清小数、分数、百分数之间的关系,理清分数与除法、商不变性质与分数基本性质之间的关系,完善知识网络。
03
能运用所学知识解决生活中的实际问题
知识梳理
考点一:分数的意义和分数单位
单位“1”:一个物体,一个计量单位或是许多物体组成的一个整体,
都可以用自然数1来表示,通常我们把它叫作单位“1”。
分 数:把单位“1”平均分成若干份,表示这样的一份或者几份的数,
叫作分数。
分数单位:把单位“1”平均分成若干份,表示其中的一份的数。
分数各部分的名称:
7
4
分数线
分子
分母
(表示平均分的份数)
(表示所取的份数)
知识梳理
考点二:分数的分类
真分数:分子比分母小的分数。
假分数:分子比分母大或者分子和分母相等的分数。
真分数<1
假分数≥1
考点三:分数的基本性质
分数的分子和分母同时乘以或者除以相同的数(零除外),分数的大小不变。
例:一个分数的分母不变,分子乘3,则这个分数( ),
如果分子不变,分母除以5,则这个分数( )。
乘3
乘5
知识梳理
考点四:分数大小的比较
分母相同的两个分数,分子大的分数比较大。
分子相同的两个分数,分母小的分数比较大。
通分:先求出原来几个分母的最小公倍数,然后把各个分数分别化成用这个最小公倍数作分母的分数。
815
?
715
?
>
911
?
1011
?
<
49
?
47
?
<
1112
?
1115
?
>
16
?
49
?
<
16
?
=
1×96×9
?
=
954
?
49
?
=
4×69×6
?
=
2454
?
知识梳理
考点五:最简分数
分子分母是互质数的分数叫最简分数。计算结果,能约分的
要约成最简分数;假分数一般要化成带分数或整数。
判断一个分数能不能化成有限小数的方法:
(1)先把这个分数化成最简分数;
(2)再看这个最简分数的分母是否只含有2和5两个质因数。
425
?
720
?
238
?
714
?
912
?
618
?
√
×
√
√
√
√
知识梳理
考点六:小数的意义
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
如 记作:0.1 记作: 0.08
1
10
8
100
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示。
小数部分的最大计数单位是十分之一,没有最小的计数单位。
小数部分有几个数位,就叫作几位小数。
知识梳理
考点七:小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字。
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
小数的末尾添上0或者去掉0,小数的大小不变。
运用小数的性质,可以在小数末尾添上0。
3.5=3.50
也可以把小数化简。 3.500=3.5
考点八:小数的性质
知识梳理
考点九:求小数的近似数
根据要求,要把小数保留到哪一位,就把这一位后面的尾数按照“四舍五入”法省略,中间用“≈”连接。
精确到十分位就是保留一位小数;
精确到百分位就是保留两位小数;
精确到千分位就是保留三位小数……
5.62975精确到十分位约:( )
5.62975精确到千分位约:( )
5.6
5.630
知识梳理
考点十:循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫作循环小数。如 0.5555…… 8.23838……
0.5555…… 记作:0.5 8.23838……记作:8.238
. .
.
按小数位数是有限还是无限分
小数
有限小数
无限小数
无限循环小数
无限不循环小数
纯循环小数
混循环小数
按小数的整数部分是否为0分
小数
纯小数
带小数(混小数)
考点十一:小数的分类
知识梳理
考点十二:百分数的意义
表示一个数是另一个数的百分之几的数叫百分数。百分数又叫百分率或百分比。
百分数后面不能带单位名称。
(百分数表示两个数的关系,不能带单位名称)
(百分数是一种特殊的分数)
(百分号用“%”表示)
知识梳理
考点十二:小数、分数、百分数之间的关系
小数:实际上是十进分数。
分数:既可以带单位表示一个具体的量,也可以表示两个量的倍数关系。
百分数:表示一个量是另一个量的百分之几,百分数不能带单位,不表示具体的量。
三者之间可以互化:0.25 = 14 = 25%
?
知识梳理
考点十三:分数与除法的关系
被除数÷除数=
被除数
除数
(除数≠0)
a÷b=
a
b
(b≠0)
表示:把单位“1”平均分成9份,取其中的5份。
米表示:把5米平均分成9份,每份是它的( ),
每份是( )米。
19
?
59
?
59
?
59
?
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
把3个苹果平均分成4份,求每份有多少个苹果,用除法计算:3÷4= (个),每份是 个苹果。这里的 表示具体的数量。
3
4
3
4
3
4
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
把一个圆平均分成4份,其中的3份用分数表示是 。
3
4
把一个正方形平均分成4份,涂色部分占其中的一份,用分数表示是 ,3个 用 ×3= 。
1
4
3
4
1
4
1
4
典例
1.用尽可能多的方式解释“ 34 ”的含义。
?
红色彩带的长度是绿色彩带长度的 。
3
4
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
(2)分数、除法之间的关系。
(3)商不变的规律与分数基本性质的关系。
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
小数的意义:小数实际是十进制分数的另一种形式,十分之一、百分之一、千分之一……的分数都可以用小数表示,如:0.1、0.01、0.001……。
分数的意义:把单位“1” 平均分成若干份,表示这样的一份或几份的数叫作分数。
百分数的意义:表示一个数是另一个数的百分之几的数叫作百分数。
典例
2.结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
小数、分数、百分数之间可以进行互化。
典例
2.结合具体的例子说一说。
(2)分数、除法之间的关系。
a÷b=???????? (b不为“0”),除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母。
?
典例
2.结合具体的例子说一说。
(3)商不变的规律与分数基本性质的关系。
商不变的规律:被除数和除数同时乘或除以相同的数(0除
外),商不变。
例如:8÷10=0.8;(8×2)÷(10×2)=0.8;
(8÷2)÷(10÷2)=0.8
分数的基本性质:分子与分母同时乘或除以相同的数(0除
外),分数的大小不变。
典例
3.想一想,填一填。
整数部分
小
数
点
小 数 部 分
···
亿 级
万 级
个 级
数位
···
千
亿
位
百
亿
位
十
亿
位
亿
位
千
万
位
百
万
位
十
万
位
万
位
千
位
百
位
十
位
个
位
·
十
分
位
百
分
位
千
分
位
万
分
位
···
计数单位
···
千
亿
百
亿
十
亿
亿
千
万
百
万
十
万
万
千
百
十
个
·
十
分
之
一
百
分
之
一
千
分
之
一
万
分
之
一
···
典例
整数和小数相邻计数单位间的进率都是( )。
10
整数部分
小
数
点
小 数 部 分
···
亿 级
万 级
个 级
数位
···
千
亿
位
百
亿
位
十
亿
位
亿
位
千
万
位
百
万
位
十
万
位
万
位
千
位
百
位
十
位
个
位
·
十
分
位
百
分
位
千
分
位
万
分
位
···
计数单位
···
千
亿
百
亿
十
亿
亿
千
万
百
万
十
万
万
千
百
十
个
·
十
分
之
一
百
分
之
一
千
分
之
一
万
分
之
一
···
变式练习
1.读一读。
从资料中你了解到什么?
你能解释一下这些数据的
具体意义吗?
变式练习
阳光小学六年级一班在调查了全班同学中近视和不近视的人数后,得到如下结果。
近视的
不近视的
占全班人数的几分之几
先把分数改写成小数,再改写成百分数。
说说你是怎样用百分数来表示上面分数的?
=0.6
=60%
≈ 0.286
=28.6%
2.从报刊中找一些分数、小数和百分数,并说一说这些数表示的具体意义。
变式练习
3.用分数表示图形中不同颜色的部分占整个图形的几分之几。
红色占_____
白色占_____
红色占_____
白色占_____
红色占_____
白色占_____
红色占_____
白色占_____
25
?
25
?
12
?
12
?
38
?
58
?
23
?
13
?
变式练习
4.在图中用阴影表示各数。
变式练习
5.在 里填上“>”“<”或“=”。
0.33
67%
25%
125%
0.78
0.8
>
>
=
>
=
<
=
=
课堂总结
今天你有什么收获?
培优拓展
1.甲数比乙数多 10.8,甲数的小数点向左移动一位就正好与乙数相等。甲乙两数分别是多少?
乙数:10.8:(10-1)=1.2
甲数:10.8+1.2=12
答:甲数是 12,乙数是1.2。
培优拓展
2.最简分数????????满足17?
a
b
因为 满足 < < ,7和6之间没有整数,
所以把 和 各自乘2
1
7
a
b
1
6
1
7
1
6
得到 < <
2
14
a
b
1
12
当 = 时不等式成立,且此时母最小,所以a+b=2+13=15。
2
13
a
b
强化练习
1.填空。
(1)( ): ( )= 0.375 = = ( )÷ 40 =( )%。
(2)134>( )> 72% 2611<( )< 360%
(3)养鸡场母鸡的只数占75%,公鸡的只数占25%。
a.母鸡的只数与鸡的总只数的比是( )。
b.公鸡的只数与鸡的总只数的比是( )。
?
3:4
1:4
375
1000
24
15
37.5
1
3
强化练习
2.判断。
(1)58吨 = 62.5%吨 ( )
(2)百分数的意义和分数完全相同。 ( )
(3)王叔叔今年纯收入相当于去年的110%,说明他家今年收入比去年高。 ( )
(4)六(1)班男同学占全班人数的60%,那么女同学占全班人数的40%。 ( )
?
x
x
√
√
强化练习
3.在图中用阴影表示各数。
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
同课章节目录
