2024-2025学年人教A版数学必修第二册8.5.1 直线与直线平行 同步练习(含详解)
文档属性
| 名称 | 2024-2025学年人教A版数学必修第二册8.5.1 直线与直线平行 同步练习(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:52:42 | ||
图片预览



文档简介
第8章 8.5 8.5.1直线与直线平行
一、选择题
1.若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
A.全等 B.相似
C.仅有一个角相等 D.无法判断
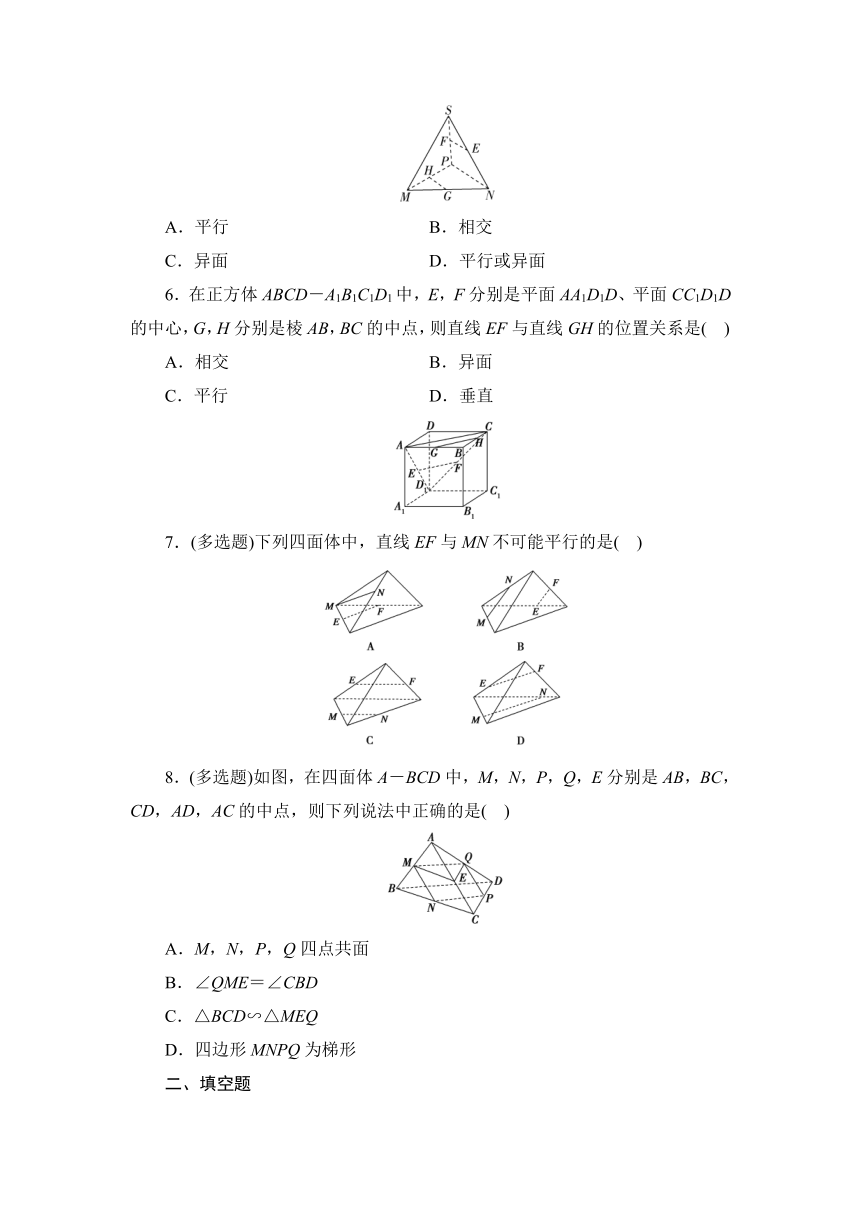
2.在三棱锥P-ABC中,PB⊥BC,E,D,F分别是AB,PA,AC的中点,则∠DEF=( )
A.30° B.45°
C.60° D.90°
3.分别和两条异面直线平行的两条直线的位置关系是( )
A.一定平行 B.一定相交
C.一定异面 D.相交或异面
4.如图,在三棱锥P-ABC中,E,F,G,H,I,J分别为线段PA,PB,PC,AB,BC,CA的中点,则下列说法正确的是( )
A.PH∥BG B.IE∥CP
C.FH∥GJ D.GI∥JH
5.如图所示,在三棱锥S-MNP中,E,F,G,H分别是棱SN,SP,MN,MP的中点,则EF与HG的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
6.在正方体ABCD-A1B1C1D1中,E,F分别是平面AA1D1D、平面CC1D1D的中心,G,H分别是棱AB,BC的中点,则直线EF与直线GH的位置关系是( )
A.相交 B.异面
C.平行 D.垂直
7.(多选题)下列四面体中,直线EF与MN不可能平行的是( )
8.(多选题)如图,在四面体A-BCD中,M,N,P,Q,E分别是AB,BC,CD,AD,AC的中点,则下列说法中正确的是( )
A.M,N,P,Q四点共面
B.∠QME=∠CBD
C.△BCD∽△MEQ
D.四边形MNPQ为梯形
二、填空题
9.如图,AA′是长方体ABCD-A′B′C′D′的一条棱,那么长方体中与AA′平行的棱共有 条.
10.已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,若==,==,则四边形EFGH形状为___.
11.如图,在空间四边形ABCD中,M,N分别是△ABC和△ACD的重心,若BD=m,则MN= .
12.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:
①AB∥CM;
②EF与MN是异面直线;
③MN∥CD.
以上结论中正确结论的序号为___.
13.a,b,c是空间中的三条直线,下面给出四个命题:
①若a∥b,b∥c,则a∥c;
②若a与b相交,b与c相交,则a与c相交;
③若a 平面α,b 平面β,则a,b一定是异面直线;
④若a,b与c成等角,则a∥b.
其中正确的命题是___(填序号).
三、解答题
14.如图所示,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)如果AC=BD,求证:四边形EFGH是菱形.
15.如图,空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且=,求证:直线EH与直线FG平行.
16.如图所示,在长方体ABCD-A1B1C1D1中的平面A1C1内有一点P,经过点P作棱BC的平行线,应该怎样画?并说明理由.
第8章 8.5 8.5.1直线与直线平行
一、选择题
1.B
由等角定理知,这两个三角形的三个角分别对应相等,所以这两个三角形相似.
2.D
如图所示,因为E,D,F分别为AB,PA,AC的中点,可得DE∥PB,EF∥BC,
又因为PB⊥BC,所以DE⊥EF,所以∠DEF=90°.
故选D.
3.D
分别与两条异面直线平行的直线不可能平行,否则,由基本性质4可得原来的两条异面直线平行,与两直线异面矛盾.但可以相交或异面.
4.C
由题意结合三角形中位线的性质,可得FH∥PA,GJ∥PA,由平行公理可得FH∥GJ.
5.A
∵E,F为中点,∴EF∥PN,
同理,HG∥PN,∴EF与HG平行.
6.C
如图,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH,故选C.
7.ABD
根据过平面内一点和平面外一点的直线,与平面内不过该点的直线异面,可判定A,B中EF,MN异面;C中直线EF与MN有可能平行;D中,若EF∥MN,则过EF的平面与底面相交,EF就跟交线平行,则过点N有两条直线与EF平行,不可能.故选ABD.
8.ABC
由中位线定理,易知MQ∥BD,ME∥BC,QE∥CD,NP∥BD.有MQ∥NP,所以M,N,P,Q四点共面,故A说法正确;根据等角定理,得∠QME=∠CBD,故B说法正确;由等角定理,知∠QME=∠DBC,∠MEQ=∠BCD,所以△BCD∽△MEQ,故C说法正确;由三角形的中位线定理,知MQ綉BD,NP綉BD,所以MQ綉NP,所以四边形MNPQ为平行四边形,故D说法不正确.
二、填空题
9. 3 .
∵四边形ABB′A′、ADD′A′均为长方形,
∴AA′∥BB′,AA′∥DD′.
又四边形BCC′B′为长方形,
∴BB′∥CC′,∴AA′∥CC′.
故与AA′平行的棱共有3条,它们分别是BB′,CC′,DD′.
10. _梯形__.
如图
在△ABD中,∵==,
∴EH∥BD且EH=BD.
在△BCD中,∵==,
∴FG∥BD且FG=BD,
∴EH∥FG且EH>FG,
∴四边形EFGH为梯形.
11. m .
连接AM并延长交BC于E,连接AN并延长交CD于F,再连接MN,EF,根据三角形重心性质得BE=EC,CF=FD.∴MN綉EF,EF綉BD.
∴MN綉BD.∴MN=m.
12. _①②__.
把正方体平面展开图还原到原来的正方体,如图所示,EF与MN是异面直线,AB∥CM,MN⊥CD,只有①②正确.
13. _①__.
由基本事实4知①正确;当a与b相交,b与c相交时,a与c可以相交、平行,也可以异面,故②不正确;a α,b β,并不能说明a与b“不同在任何一个平面内”,故③不正确;当a,b与c成等角时,a与b可以相交、平行,也可以异面,故④不正确.
三、解答题
14.
(1)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EF∥AC,HG∥AC,EF=HG=AC,
所以EF∥HG,EF=HG,
所以四边形EFGH是平行四边形.
(2)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EH∥BD,EH=BD.
因为EF=AC,AC=BD,所以EH=EF.
又因为四边形EFGH是平行四边形,所以四边形EFGH是菱形.
15.
∵E、H分别是AB、AD的中点,则EH∥BD,
又∵F、G分别是BC、CD上的点,且=,则FG∥BD,
∴EH∥FG,
故直线EH与直线FG平行.
16.
如图所示,在平面A1C1内过P作直线EF∥B1C1,交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF∥B1C1,BC∥B1C1,所以EF∥BC.
一、选择题
1.若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
A.全等 B.相似
C.仅有一个角相等 D.无法判断
2.在三棱锥P-ABC中,PB⊥BC,E,D,F分别是AB,PA,AC的中点,则∠DEF=( )
A.30° B.45°
C.60° D.90°
3.分别和两条异面直线平行的两条直线的位置关系是( )
A.一定平行 B.一定相交
C.一定异面 D.相交或异面
4.如图,在三棱锥P-ABC中,E,F,G,H,I,J分别为线段PA,PB,PC,AB,BC,CA的中点,则下列说法正确的是( )
A.PH∥BG B.IE∥CP
C.FH∥GJ D.GI∥JH
5.如图所示,在三棱锥S-MNP中,E,F,G,H分别是棱SN,SP,MN,MP的中点,则EF与HG的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
6.在正方体ABCD-A1B1C1D1中,E,F分别是平面AA1D1D、平面CC1D1D的中心,G,H分别是棱AB,BC的中点,则直线EF与直线GH的位置关系是( )
A.相交 B.异面
C.平行 D.垂直
7.(多选题)下列四面体中,直线EF与MN不可能平行的是( )
8.(多选题)如图,在四面体A-BCD中,M,N,P,Q,E分别是AB,BC,CD,AD,AC的中点,则下列说法中正确的是( )
A.M,N,P,Q四点共面
B.∠QME=∠CBD
C.△BCD∽△MEQ
D.四边形MNPQ为梯形
二、填空题
9.如图,AA′是长方体ABCD-A′B′C′D′的一条棱,那么长方体中与AA′平行的棱共有 条.
10.已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,若==,==,则四边形EFGH形状为___.
11.如图,在空间四边形ABCD中,M,N分别是△ABC和△ACD的重心,若BD=m,则MN= .
12.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:
①AB∥CM;
②EF与MN是异面直线;
③MN∥CD.
以上结论中正确结论的序号为___.
13.a,b,c是空间中的三条直线,下面给出四个命题:
①若a∥b,b∥c,则a∥c;
②若a与b相交,b与c相交,则a与c相交;
③若a 平面α,b 平面β,则a,b一定是异面直线;
④若a,b与c成等角,则a∥b.
其中正确的命题是___(填序号).
三、解答题
14.如图所示,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)如果AC=BD,求证:四边形EFGH是菱形.
15.如图,空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且=,求证:直线EH与直线FG平行.
16.如图所示,在长方体ABCD-A1B1C1D1中的平面A1C1内有一点P,经过点P作棱BC的平行线,应该怎样画?并说明理由.
第8章 8.5 8.5.1直线与直线平行
一、选择题
1.B
由等角定理知,这两个三角形的三个角分别对应相等,所以这两个三角形相似.
2.D
如图所示,因为E,D,F分别为AB,PA,AC的中点,可得DE∥PB,EF∥BC,
又因为PB⊥BC,所以DE⊥EF,所以∠DEF=90°.
故选D.
3.D
分别与两条异面直线平行的直线不可能平行,否则,由基本性质4可得原来的两条异面直线平行,与两直线异面矛盾.但可以相交或异面.
4.C
由题意结合三角形中位线的性质,可得FH∥PA,GJ∥PA,由平行公理可得FH∥GJ.
5.A
∵E,F为中点,∴EF∥PN,
同理,HG∥PN,∴EF与HG平行.
6.C
如图,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH,故选C.
7.ABD
根据过平面内一点和平面外一点的直线,与平面内不过该点的直线异面,可判定A,B中EF,MN异面;C中直线EF与MN有可能平行;D中,若EF∥MN,则过EF的平面与底面相交,EF就跟交线平行,则过点N有两条直线与EF平行,不可能.故选ABD.
8.ABC
由中位线定理,易知MQ∥BD,ME∥BC,QE∥CD,NP∥BD.有MQ∥NP,所以M,N,P,Q四点共面,故A说法正确;根据等角定理,得∠QME=∠CBD,故B说法正确;由等角定理,知∠QME=∠DBC,∠MEQ=∠BCD,所以△BCD∽△MEQ,故C说法正确;由三角形的中位线定理,知MQ綉BD,NP綉BD,所以MQ綉NP,所以四边形MNPQ为平行四边形,故D说法不正确.
二、填空题
9. 3 .
∵四边形ABB′A′、ADD′A′均为长方形,
∴AA′∥BB′,AA′∥DD′.
又四边形BCC′B′为长方形,
∴BB′∥CC′,∴AA′∥CC′.
故与AA′平行的棱共有3条,它们分别是BB′,CC′,DD′.
10. _梯形__.
如图
在△ABD中,∵==,
∴EH∥BD且EH=BD.
在△BCD中,∵==,
∴FG∥BD且FG=BD,
∴EH∥FG且EH>FG,
∴四边形EFGH为梯形.
11. m .
连接AM并延长交BC于E,连接AN并延长交CD于F,再连接MN,EF,根据三角形重心性质得BE=EC,CF=FD.∴MN綉EF,EF綉BD.
∴MN綉BD.∴MN=m.
12. _①②__.
把正方体平面展开图还原到原来的正方体,如图所示,EF与MN是异面直线,AB∥CM,MN⊥CD,只有①②正确.
13. _①__.
由基本事实4知①正确;当a与b相交,b与c相交时,a与c可以相交、平行,也可以异面,故②不正确;a α,b β,并不能说明a与b“不同在任何一个平面内”,故③不正确;当a,b与c成等角时,a与b可以相交、平行,也可以异面,故④不正确.
三、解答题
14.
(1)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EF∥AC,HG∥AC,EF=HG=AC,
所以EF∥HG,EF=HG,
所以四边形EFGH是平行四边形.
(2)因为空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,
所以EH∥BD,EH=BD.
因为EF=AC,AC=BD,所以EH=EF.
又因为四边形EFGH是平行四边形,所以四边形EFGH是菱形.
15.
∵E、H分别是AB、AD的中点,则EH∥BD,
又∵F、G分别是BC、CD上的点,且=,则FG∥BD,
∴EH∥FG,
故直线EH与直线FG平行.
16.
如图所示,在平面A1C1内过P作直线EF∥B1C1,交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF∥B1C1,BC∥B1C1,所以EF∥BC.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
