沪科版七下(2024版)10.2.4 平行线的判定方法2、3 学案
文档属性
| 名称 | 沪科版七下(2024版)10.2.4 平行线的判定方法2、3 学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 649.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第10章 相交线、平行线与平移
10.2.4 平行线的判定方法2、3
学习目标与重难点
学习目标:
1.理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。
2.能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。
3.经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
学习重点:
掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法,并能用其进行简单的推理。
学习难点:
从同位角判定方法迁移到内错角和同旁内角的判定方法,理解三种判定方法之间的联系;规范书写推理过程,做到逻辑严谨、语言准确。
教学过程
一、复习回顾
基本事实:两条直线被第三条直线所截,如果同位角________,那么这两条直线________.
简单地说,同位角________,两直线________.
几何语言
∵∠1=∠2
∴________________________________________
二、新知探究
探究一:平行线的判定方法2
教材第141页
思考:如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗?
【归纳】
平行线的判断方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(内错角相等,两直线平行)
利用内错角相等来判定两直线平行的方法:
______________________________________________________________________________________________________________________________________________________________________________探究二:平行线的判定方法3
教材第142页
思考:如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗?
【归纳】
平行线的判断方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
几何语言
∵∠1+∠2=180°
∴ AB∥ CD(同旁内角互补,两直线平行)
利用同旁内角互补来判定两直线平行的方法:
______________________________________________________________________________________________________________________________________________________________________________
三、课堂练习
【知识技能类作业】
必做题
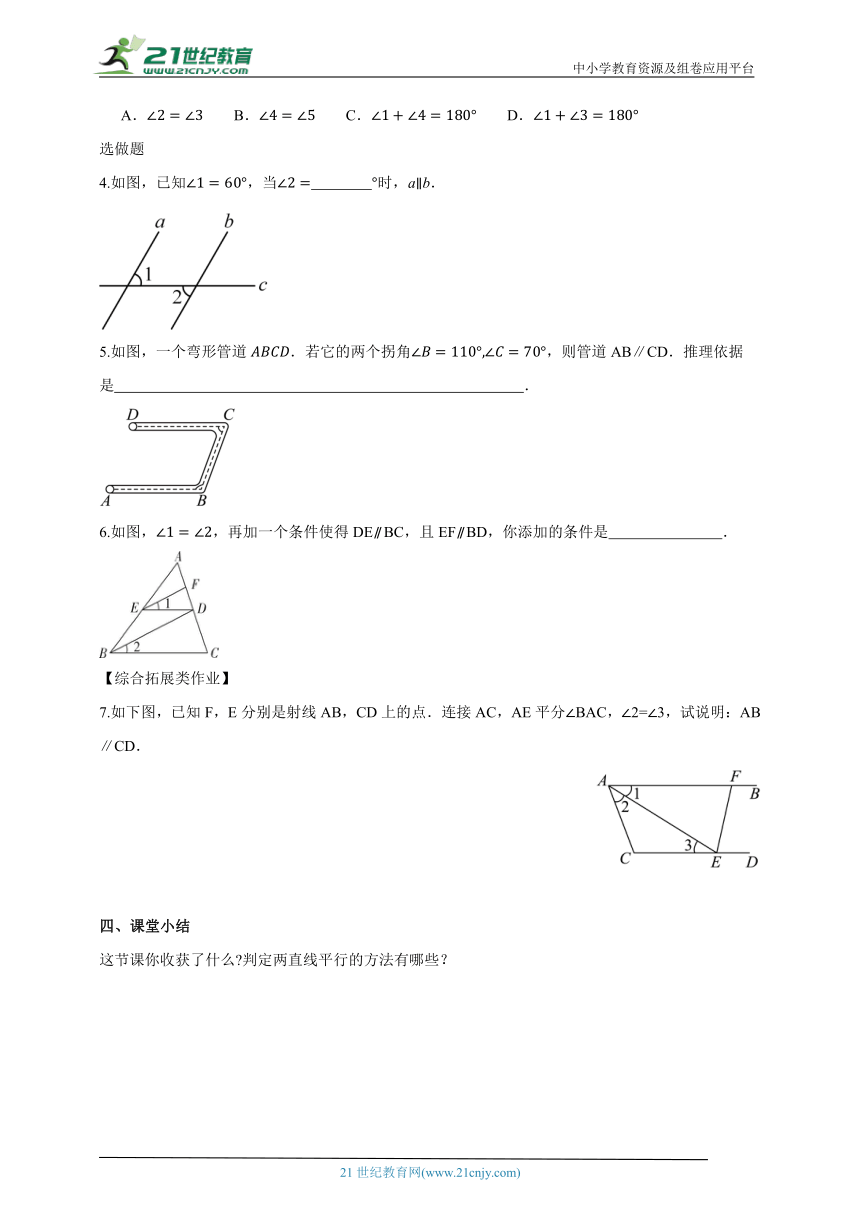
1.如图,下列条件能判定AD∥ BC的是( )
A. B. C. D.
2.如图,下列能判定AD∥ BC的条件有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
3.如图,已知四条直线,下列不能判断a∥ b的是( )
A. B. C. D.
选做题
4.如图,已知,当 时,a∥b.
5.如图,一个弯形管道.若它的两个拐角,则管道AB∥CD.推理依据是 .
6.如图,,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 .
【综合拓展类作业】
7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥CD.
四、课堂小结
这节课你收获了什么 判定两直线平行的方法有哪些?
五、作业布置
1.如图,下列条件不能判定CF∥ BE的是( )
A. B. C. D.
2.如图,下列条件中,不能判断直线a∥ b的是( )
A. B. C. D.
3.如图,有以下条件:①;②;③;④;⑤.其中能判断AB∥CD的条件有 (填序号).
4.如图,已知点C、B分别在线段、上,,.求证:AE∥DF.
答案解析
课堂练习:
1.【答案】B
【解析】解:A、能判定,故不符合题意;
B、能判定,符合题意;
C、不能判定,故不符合题意;
D、不能判定,故不符合题意;
故选:B.
2.【答案】C
【解析】解:①,
,故符合题意;
②,
,故不符合题意;
③,
,故符合题意;
④,
,故符合题意;
⑤,
,故不符合题意,
能判定的条件有①③④,共3个,
故选:C.
3.【答案】C
【解析】解:A.根据同位角相等,两直线平行,由,能判断直线;
B.根据内错角相等,两直线平行,由,能判断直线;
C.由,不能判断直线;
D.由,,可得,根据同位角相等,两直线平行,能判断直线;
故选:C.
4.【答案】60
【解析】解:∵只有当时,,
又∵,
∴当时,.
故答案为:.
5.【答案】同旁内角互补,两直线平行.
【解析】解:∵,
∴,
∴(同旁内角互补,两直线平行).
故答案为:同旁内角互补,两直线平行.
6.【答案】(答案不唯一)
【解析】解:添加条件,理由如下:
∵,,
∴,
∴,
∴,且,
添加条件,同理可证.
故答案为:(答案不唯一).
7.【答案】【解析】
解:平分,
.
,
,
.
作业布置:
1.【答案】B
【解析】解:A、,则,故不符合题意;
B、,则,故符合题意;
C、,则,故不符合题意;
D、,则,故不符合题意;
故选:B
2.【答案】B
【解析】解:∵,
∴,故A选项不符合题意;
∵,
∴,故C选项不符合题意;
∵,
∴,故D选项不符合题意;
∵,
∴不一定平行,故B选项符合题意,
故选:B.
3.【答案】D
【解析】要使分式的值为零,则分子,且分母,
由,解得或,
又因为分母,即,
所以.
故选:D.
4.【答案】证明:∵∠1=∠2,
∴CD∥ AB,
∴∠D+∠ABD=180°,
∵∠A=∠D,
∴∠A+∠ABD=180°,
∴AE∥ DF(同旁内角互补,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第10章 相交线、平行线与平移
10.2.4 平行线的判定方法2、3
学习目标与重难点
学习目标:
1.理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。
2.能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。
3.经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
学习重点:
掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法,并能用其进行简单的推理。
学习难点:
从同位角判定方法迁移到内错角和同旁内角的判定方法,理解三种判定方法之间的联系;规范书写推理过程,做到逻辑严谨、语言准确。
教学过程
一、复习回顾
基本事实:两条直线被第三条直线所截,如果同位角________,那么这两条直线________.
简单地说,同位角________,两直线________.
几何语言
∵∠1=∠2
∴________________________________________
二、新知探究
探究一:平行线的判定方法2
教材第141页
思考:如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗?
【归纳】
平行线的判断方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(内错角相等,两直线平行)
利用内错角相等来判定两直线平行的方法:
______________________________________________________________________________________________________________________________________________________________________________探究二:平行线的判定方法3
教材第142页
思考:如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗?
【归纳】
平行线的判断方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
几何语言
∵∠1+∠2=180°
∴ AB∥ CD(同旁内角互补,两直线平行)
利用同旁内角互补来判定两直线平行的方法:
______________________________________________________________________________________________________________________________________________________________________________
三、课堂练习
【知识技能类作业】
必做题
1.如图,下列条件能判定AD∥ BC的是( )
A. B. C. D.
2.如图,下列能判定AD∥ BC的条件有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
3.如图,已知四条直线,下列不能判断a∥ b的是( )
A. B. C. D.
选做题
4.如图,已知,当 时,a∥b.
5.如图,一个弯形管道.若它的两个拐角,则管道AB∥CD.推理依据是 .
6.如图,,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 .
【综合拓展类作业】
7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥CD.
四、课堂小结
这节课你收获了什么 判定两直线平行的方法有哪些?
五、作业布置
1.如图,下列条件不能判定CF∥ BE的是( )
A. B. C. D.
2.如图,下列条件中,不能判断直线a∥ b的是( )
A. B. C. D.
3.如图,有以下条件:①;②;③;④;⑤.其中能判断AB∥CD的条件有 (填序号).
4.如图,已知点C、B分别在线段、上,,.求证:AE∥DF.
答案解析
课堂练习:
1.【答案】B
【解析】解:A、能判定,故不符合题意;
B、能判定,符合题意;
C、不能判定,故不符合题意;
D、不能判定,故不符合题意;
故选:B.
2.【答案】C
【解析】解:①,
,故符合题意;
②,
,故不符合题意;
③,
,故符合题意;
④,
,故符合题意;
⑤,
,故不符合题意,
能判定的条件有①③④,共3个,
故选:C.
3.【答案】C
【解析】解:A.根据同位角相等,两直线平行,由,能判断直线;
B.根据内错角相等,两直线平行,由,能判断直线;
C.由,不能判断直线;
D.由,,可得,根据同位角相等,两直线平行,能判断直线;
故选:C.
4.【答案】60
【解析】解:∵只有当时,,
又∵,
∴当时,.
故答案为:.
5.【答案】同旁内角互补,两直线平行.
【解析】解:∵,
∴,
∴(同旁内角互补,两直线平行).
故答案为:同旁内角互补,两直线平行.
6.【答案】(答案不唯一)
【解析】解:添加条件,理由如下:
∵,,
∴,
∴,
∴,且,
添加条件,同理可证.
故答案为:(答案不唯一).
7.【答案】【解析】
解:平分,
.
,
,
.
作业布置:
1.【答案】B
【解析】解:A、,则,故不符合题意;
B、,则,故符合题意;
C、,则,故不符合题意;
D、,则,故不符合题意;
故选:B
2.【答案】B
【解析】解:∵,
∴,故A选项不符合题意;
∵,
∴,故C选项不符合题意;
∵,
∴,故D选项不符合题意;
∵,
∴不一定平行,故B选项符合题意,
故选:B.
3.【答案】D
【解析】要使分式的值为零,则分子,且分母,
由,解得或,
又因为分母,即,
所以.
故选:D.
4.【答案】证明:∵∠1=∠2,
∴CD∥ AB,
∴∠D+∠ABD=180°,
∵∠A=∠D,
∴∠A+∠ABD=180°,
∴AE∥ DF(同旁内角互补,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
