沪科版七下(2024版)10.2.4 平行线的判定方法2、3 教案
文档属性
| 名称 | 沪科版七下(2024版)10.2.4 平行线的判定方法2、3 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 468.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 14:39:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《10.2.4 平行线的判定方法2、3》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《10.2.4 平行线的判定方法2、3》是沪科版七年级下册第10章《相交线、平行线与平移》的第二节第四课时的内容。本节课是平行线判定方法的核心内容,在“同位角相等,两直线平行”的基础上,进一步探究“内错角相等,两直线平行”和“同旁内角互补,两直线平行”两种判定方法。教材注重几何语言的规范使用,强调推理过程的严谨性,让学生经历从实验几何到论证几何的过渡,为后续学习平行线的性质和三角形、四边形等知识奠定基础,在平面几何知识体系中起着承上启下的作用。
学习者分析 七年级学生在之前的学习中已经掌握了平行线的定义、同位角的概念以及“同位角相等,两直线平行”的判定方法,具备了一定的几何基础和逻辑推理能力。但对于内错角、同旁内角与两直线平行的关系,学生理解起来可能存在一定困难,尤其是如何从同位角判定方法迁移到内错角和同旁内角的判定方法,需要教师进行引导。此外,学生在书写推理过程时,可能会出现逻辑不严谨、几何语言使用不规范等问题,需要加强训练。
教学目标 1.理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。 2.能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。 3.经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
教学重点 掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法,并能用其进行简单的推理。
教学难点 从同位角判定方法迁移到内错角和同旁内角的判定方法,理解三种判定方法之间的联系;规范书写推理过程,做到逻辑严谨、语言准确。
学习活动设计
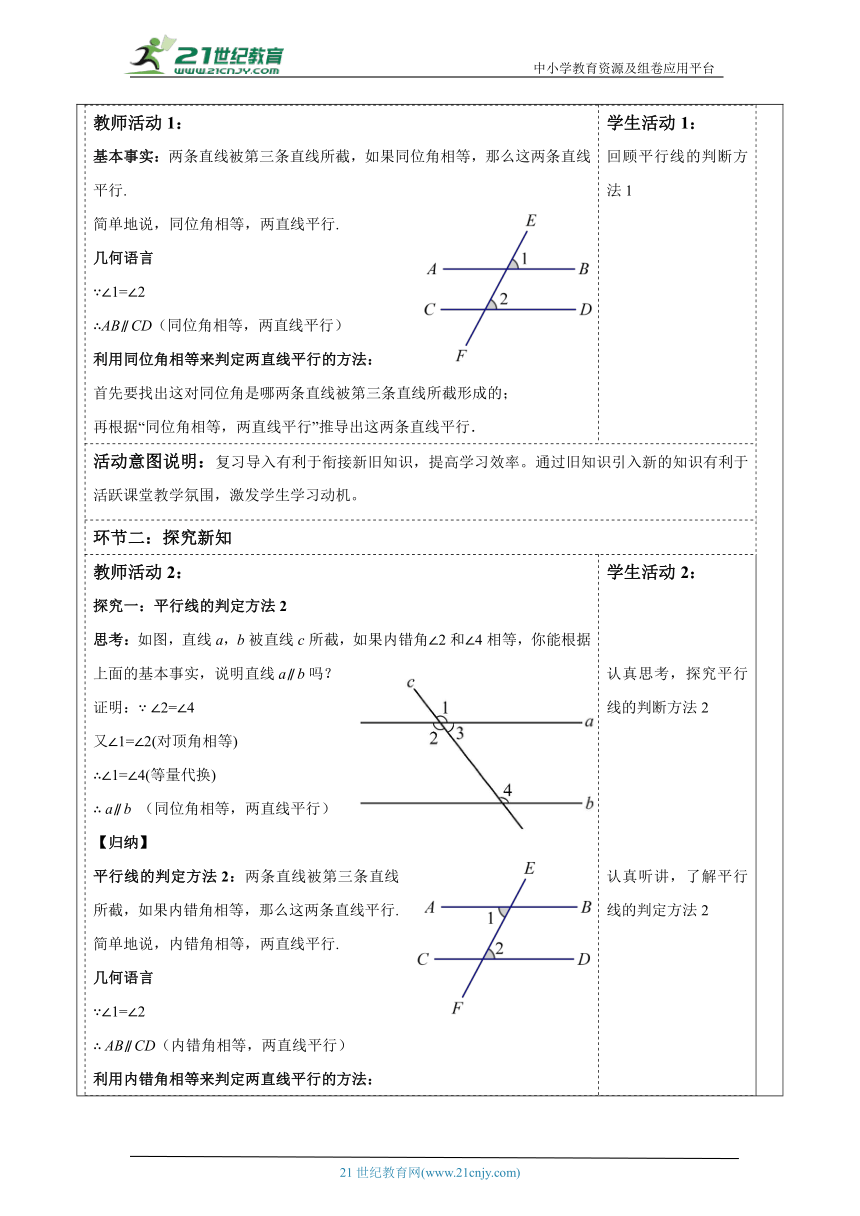
教师活动学生活动环节一:新知导入教师活动1: 基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行. 几何语言 ∵∠1=∠2 ∴AB∥ CD(同位角相等,两直线平行) 利用同位角相等来判定两直线平行的方法: 首先要找出这对同位角是哪两条直线被第三条直线所截形成的; 再根据“同位角相等,两直线平行”推导出这两条直线平行.学生活动1: 回顾平行线的判断方法1活动意图说明:复习导入有利于衔接新旧知识,提高学习效率。通过旧知识引入新的知识有利于活跃课堂教学氛围,激发学生学习动机。环节二:探究新知教师活动2: 探究一:平行线的判定方法2 思考:如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗? 证明:∵ ∠2=∠4 又∠1=∠2(对顶角相等) ∴∠1=∠4(等量代换) ∴ a∥ b (同位角相等,两直线平行) 【归纳】 平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单地说,内错角相等,两直线平行. 几何语言 ∵∠1=∠2 ∴ AB∥ CD(内错角相等,两直线平行) 利用内错角相等来判定两直线平行的方法: (1)看两角是不是两直线被第三条直线截得的角; (2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行. 探究二:平行线的判定方法3 思考:如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗? 法1 证明:∵ ∠3+∠4=180° 又∠1+∠3=180° ∴∠4=∠1 ∴ a∥ b (同位角相等,两直线平行) 法2 证明:∵ ∠3+∠4=180° 又∠2+∠3=180° ∴∠4=∠2 ∴ a∥ b (内错角相等,两直线平行) 【归纳】 平行线的判断方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 简单地说,同旁内角互补,两直线平行. 几何语言 ∵∠1+∠2=180° ∴ AB∥ CD(同旁内角互补,两直线平行) 利用同旁内角互补来判定两直线平行的方法: (1)看两角是不是两直线被第三条直线截得的角; (2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.学生活动2: 认真思考,探究平行线的判断方法2 认真听讲,了解平行线的判定方法2 认真思考,探究平行线的判断方法3 认真听讲 认真听讲,了解平行线的判定方法3 活动意图说明:数学是一门严谨的学科,它要求推理过程和结论都必须经过严格的逻辑推理和证明。让学生通过自主证明,感受数学的严谨性,提高学生的逻辑推理能力和自主解题能力。环节三:课堂总结教师活动3: 判定两直线平行的方法 1. 直线的位置关系: (1)同一平面内不相交的两条直线平行 . (2)同平行于第三条直线的两条直线平行 . 2. 角的大小关系:同位角相等,两直线平行. 内错角相等,两直线平行. 同旁内角互补,两直线平行.学生活动4: 学生跟随教师对学习内容进行归纳梳理 活动意图说明:对课堂教学进行归纳梳理,给学生一个整体印象,促进学生掌握知识总结规律。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如图,下列条件能判定AD∥BC的是( ) A. B. C. D. 2.如图,下列能判定AD∥BC的条件有( ) ①;②;③;④;⑤ A.1个 B.2个 C.3个 D.4个 3.如图,已知四条直线,下列不能判断a∥b的是( ) A. B. C. D. 选做题: 4.如图,已知,当 时,a∥b. 5.如图,一个弯形管道.若它的两个拐角,则管道AB∥CD.推理依据是 . 6.如图,,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 . 【综合拓展类作业】 7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥CD.
作业设计 【知识技能类作业】 必做题: 1.如图,下列条件不能判定CF∥BE的是( ) A. B. C. D. 2.如图,下列条件中,不能判断直线a∥b的是( ) A. B. C. D. 3.如图,有以下条件:①;②;③;④;⑤.其中能判断AB∥CD的条件有 (填序号). 【综合拓展类作业】 4.如图,已知点C、B分别在线段、上,,.求证:AE∥DF.
教学反思 本节课通过复习同位角判定方法引入新课,引导学生类比探究内错角、同旁内角与两直线平行的关系,符合学生的认知规律,大部分学生能够积极参与探究活动。在教学过程中,通过让学生自主画图、测量、推理,培养了学生的动手能力和逻辑思维能力。然而,在课堂练习中发现,部分学生在运用内错角和同旁内角判定方法时,仍然会出现混淆的情况,对推理过程的书写也不够规范。针对这些问题,在今后的教学中,应加强对比练习,让学生更清晰地理解三种判定方法的区别和联系;同时,增加推理过程的书写训练,严格要求,及时反馈,提高学生的推理能力和几何语言表达能力。此外,还应关注学生的个体差异,对于学习困难的学生给予更多的指导和帮助,确保每个学生都能掌握所学知识。
21世纪教育网(www.21cnjy.com)
分课时教学设计
《10.2.4 平行线的判定方法2、3》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《10.2.4 平行线的判定方法2、3》是沪科版七年级下册第10章《相交线、平行线与平移》的第二节第四课时的内容。本节课是平行线判定方法的核心内容,在“同位角相等,两直线平行”的基础上,进一步探究“内错角相等,两直线平行”和“同旁内角互补,两直线平行”两种判定方法。教材注重几何语言的规范使用,强调推理过程的严谨性,让学生经历从实验几何到论证几何的过渡,为后续学习平行线的性质和三角形、四边形等知识奠定基础,在平面几何知识体系中起着承上启下的作用。
学习者分析 七年级学生在之前的学习中已经掌握了平行线的定义、同位角的概念以及“同位角相等,两直线平行”的判定方法,具备了一定的几何基础和逻辑推理能力。但对于内错角、同旁内角与两直线平行的关系,学生理解起来可能存在一定困难,尤其是如何从同位角判定方法迁移到内错角和同旁内角的判定方法,需要教师进行引导。此外,学生在书写推理过程时,可能会出现逻辑不严谨、几何语言使用不规范等问题,需要加强训练。
教学目标 1.理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。 2.能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。 3.经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
教学重点 掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法,并能用其进行简单的推理。
教学难点 从同位角判定方法迁移到内错角和同旁内角的判定方法,理解三种判定方法之间的联系;规范书写推理过程,做到逻辑严谨、语言准确。
学习活动设计
教师活动学生活动环节一:新知导入教师活动1: 基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行. 几何语言 ∵∠1=∠2 ∴AB∥ CD(同位角相等,两直线平行) 利用同位角相等来判定两直线平行的方法: 首先要找出这对同位角是哪两条直线被第三条直线所截形成的; 再根据“同位角相等,两直线平行”推导出这两条直线平行.学生活动1: 回顾平行线的判断方法1活动意图说明:复习导入有利于衔接新旧知识,提高学习效率。通过旧知识引入新的知识有利于活跃课堂教学氛围,激发学生学习动机。环节二:探究新知教师活动2: 探究一:平行线的判定方法2 思考:如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗? 证明:∵ ∠2=∠4 又∠1=∠2(对顶角相等) ∴∠1=∠4(等量代换) ∴ a∥ b (同位角相等,两直线平行) 【归纳】 平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单地说,内错角相等,两直线平行. 几何语言 ∵∠1=∠2 ∴ AB∥ CD(内错角相等,两直线平行) 利用内错角相等来判定两直线平行的方法: (1)看两角是不是两直线被第三条直线截得的角; (2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行. 探究二:平行线的判定方法3 思考:如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗? 法1 证明:∵ ∠3+∠4=180° 又∠1+∠3=180° ∴∠4=∠1 ∴ a∥ b (同位角相等,两直线平行) 法2 证明:∵ ∠3+∠4=180° 又∠2+∠3=180° ∴∠4=∠2 ∴ a∥ b (内错角相等,两直线平行) 【归纳】 平行线的判断方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 简单地说,同旁内角互补,两直线平行. 几何语言 ∵∠1+∠2=180° ∴ AB∥ CD(同旁内角互补,两直线平行) 利用同旁内角互补来判定两直线平行的方法: (1)看两角是不是两直线被第三条直线截得的角; (2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.学生活动2: 认真思考,探究平行线的判断方法2 认真听讲,了解平行线的判定方法2 认真思考,探究平行线的判断方法3 认真听讲 认真听讲,了解平行线的判定方法3 活动意图说明:数学是一门严谨的学科,它要求推理过程和结论都必须经过严格的逻辑推理和证明。让学生通过自主证明,感受数学的严谨性,提高学生的逻辑推理能力和自主解题能力。环节三:课堂总结教师活动3: 判定两直线平行的方法 1. 直线的位置关系: (1)同一平面内不相交的两条直线平行 . (2)同平行于第三条直线的两条直线平行 . 2. 角的大小关系:同位角相等,两直线平行. 内错角相等,两直线平行. 同旁内角互补,两直线平行.学生活动4: 学生跟随教师对学习内容进行归纳梳理 活动意图说明:对课堂教学进行归纳梳理,给学生一个整体印象,促进学生掌握知识总结规律。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如图,下列条件能判定AD∥BC的是( ) A. B. C. D. 2.如图,下列能判定AD∥BC的条件有( ) ①;②;③;④;⑤ A.1个 B.2个 C.3个 D.4个 3.如图,已知四条直线,下列不能判断a∥b的是( ) A. B. C. D. 选做题: 4.如图,已知,当 时,a∥b. 5.如图,一个弯形管道.若它的两个拐角,则管道AB∥CD.推理依据是 . 6.如图,,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 . 【综合拓展类作业】 7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥CD.
作业设计 【知识技能类作业】 必做题: 1.如图,下列条件不能判定CF∥BE的是( ) A. B. C. D. 2.如图,下列条件中,不能判断直线a∥b的是( ) A. B. C. D. 3.如图,有以下条件:①;②;③;④;⑤.其中能判断AB∥CD的条件有 (填序号). 【综合拓展类作业】 4.如图,已知点C、B分别在线段、上,,.求证:AE∥DF.
教学反思 本节课通过复习同位角判定方法引入新课,引导学生类比探究内错角、同旁内角与两直线平行的关系,符合学生的认知规律,大部分学生能够积极参与探究活动。在教学过程中,通过让学生自主画图、测量、推理,培养了学生的动手能力和逻辑思维能力。然而,在课堂练习中发现,部分学生在运用内错角和同旁内角判定方法时,仍然会出现混淆的情况,对推理过程的书写也不够规范。针对这些问题,在今后的教学中,应加强对比练习,让学生更清晰地理解三种判定方法的区别和联系;同时,增加推理过程的书写训练,严格要求,及时反馈,提高学生的推理能力和几何语言表达能力。此外,还应关注学生的个体差异,对于学习困难的学生给予更多的指导和帮助,确保每个学生都能掌握所学知识。
21世纪教育网(www.21cnjy.com)
