沪科版七下(2024版)10.2.4 平行线的判定方法2、3 课件
文档属性
| 名称 | 沪科版七下(2024版)10.2.4 平行线的判定方法2、3 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
第10章 相交线、平行线与平移
10.2.4 平行线的判定方法2、3
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。
01
能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。
02
经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
03
02
新知导入
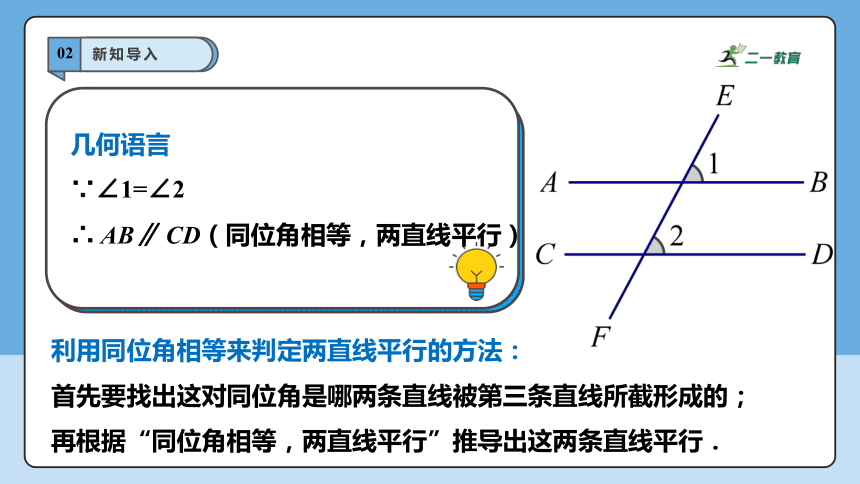
几何语言
∵∠1=∠2
∴ AB∥ CD(同位角相等,两直线平行)
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;
再根据“同位角相等,两直线平行”推导出这两条直线平行.
思考
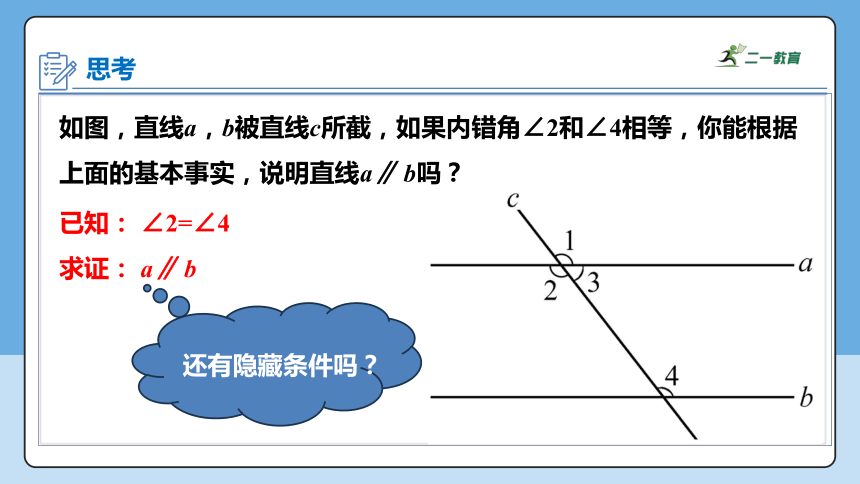
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗?
已知: ∠2=∠4
求证: a∥ b
还有隐藏条件吗?
03
新知探究
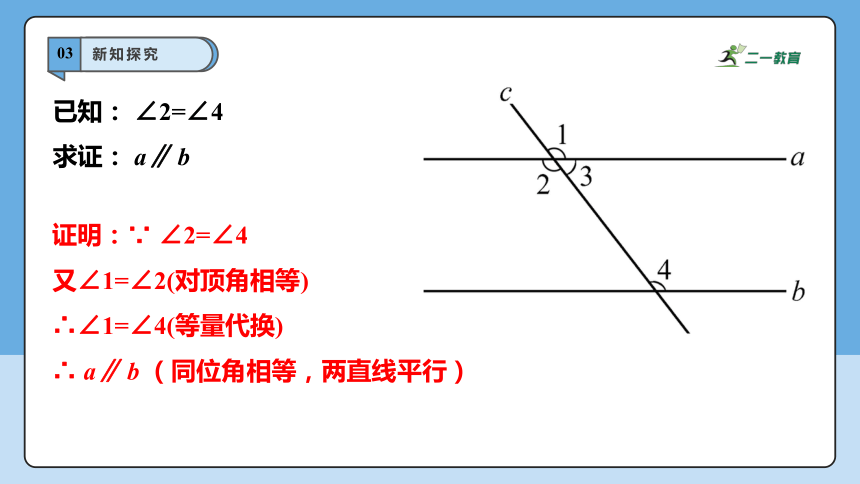
已知: ∠2=∠4
求证: a∥ b
证明:∵ ∠2=∠4
又∠1=∠2(对顶角相等)
∴∠1=∠4(等量代换)
∴ a∥ b (同位角相等,两直线平行)
03
新知探究
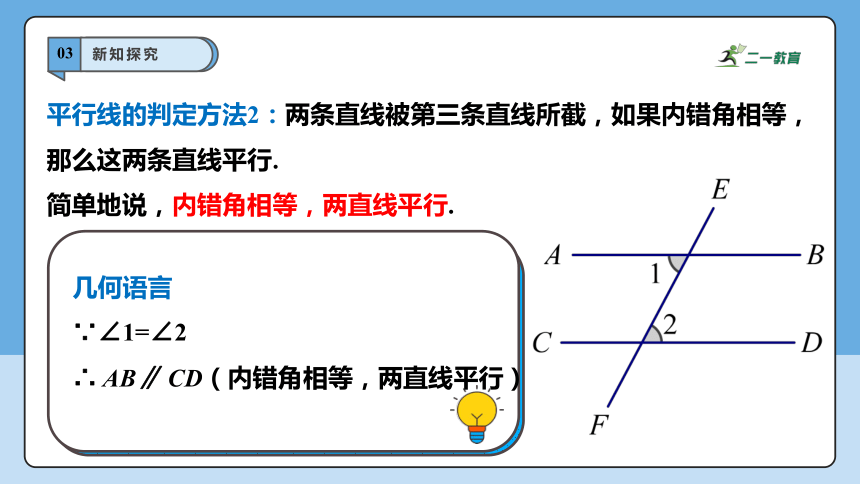
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(内错角相等,两直线平行)
03
新知探究
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
思考
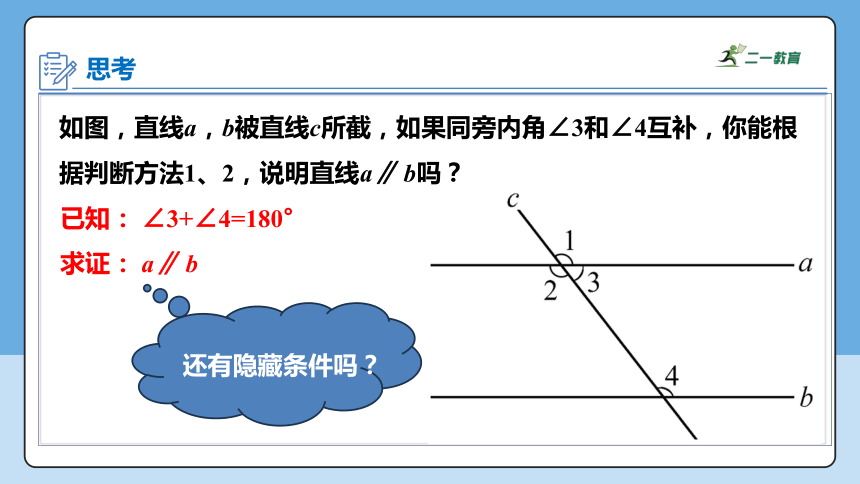
如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗?
已知: ∠3+∠4=180°
求证: a∥ b
还有隐藏条件吗?
03
新知探究
已知: ∠3+∠4=180°
求证: a∥ b
证明:∵ ∠3+∠4=180°
又∠1+∠3=180°
∴∠4=∠1
∴ a∥ b (同位角相等,两直线平行)
判定方法1
03
新知探究
已知: ∠3+∠4=180°
求证: a∥ b
证明:∵ ∠3+∠4=180°
又∠2+∠3=180°
∴∠4=∠2
∴ a∥ b (内错角相等,两直线平行)
判定方法2
03
新知探究
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
几何语言
∵∠1+∠2=180°
∴ AB∥ CD(同旁内角互补,两直线平行)
03
新知探究
利用同旁内角互补来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.
04
课堂练习
【知识技能类作业】必做题:
1.如图,下列条件能判定AD∥ BC的是( )
A.∠D=∠EAD
B.∠C+∠D=180°
C.∠B=∠D
D.∠B=∠C
B
04
课堂练习
【知识技能类作业】必做题:
2.如图,下列能判定AD∥BC的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4 ;④∠B=∠5;⑤∠D=∠5
A.1个 B.2个 C.3个 D.4个
C
04
课堂练习
【知识技能类作业】必做题:
3.如图,已知a,b,c,d四条直线,下列不能判断a∥ b的是( )
A.∠2=∠3
B.∠4=∠5
C.∠1+∠4=180°
D.∠1+∠3=180°
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,已知∠1=60°,当∠2= °时,a∥ b.
60
04
课堂练习
【知识技能类作业】选做题:
5.如图,一个弯形管道ABCD.若它的两个拐角∠B=110°,∠C=70°,则管道AB∥CD.推理依据是 .
同旁内角互补,两直线平行
04
课堂练习
【知识技能类作业】选做题:
6.如图,∠1=∠2,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 .
∠BDE=∠1(答案不唯一)
04
课堂练习
【综合拓展类作业】
7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥ CD.
解:∵AE平分∠BAC,
∴∠1=∠2.
∵∠2=∠3,
∴∠1=∠3,
∴ AB∥ CD(内错角相等,两直线平行) .
05
课堂小结
判定两直线平行的方法
1. 直线的位置关系:
(1)同一平面内不相交的两条直线平行 .
(2)同平行于第三条直线的两条直线平行 .
2. 角的大小关系:同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
06
作业布置
【知识技能类作业】
1.如图,下列条件不能判定CF∥BE的是( )
A.∠1=∠B
B.∠1=∠C
C.∠CFB+∠B=180°
D.∠CFP=∠FPB
B
06
作业布置
【知识技能类作业】
2.如图,下列条件中,不能判断直线a∥ b的是( )
A.∠1=∠3
B.∠2=∠3
C.∠4=∠5
D.∠2+∠4=180°
B
06
作业布置
【知识技能类作业】
3.如图,有以下条件:①∠1=∠2;②∠3=∠4;③∠1+∠3+∠BGC=180°;④∠1+∠3=∠2+∠4;⑤∠E=∠F,∠1=∠2.其中能判断AB∥ CD的条件有
(填序号).
③④⑤
06
作业布置
【综合拓展类作业】
4.如图,已知点C、B分别在线段AE、DF上,∠1=∠2,∠A=∠D.求证:AE∥ DF.
证明:∵∠1=∠2,
∴CD∥ AB,
∴∠D+∠ABD=180°,
∵∠A=∠D,
∴∠A+∠ABD=180°,
∴AE∥ DF(同旁内角互补,两直线平行).
07
板书设计
判断方法2:
几何语言:
判断方法3:
几何语言:
10.2.4 平行线的判定方法2、3
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第10章 相交线、平行线与平移
10.2.4 平行线的判定方法2、3
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解并掌握“内错角相等,两直线平行”和“同旁内角互补,两直线平行”这两种判定方法。
01
能够运用判断方法方法判断两直线是否平行,并规范书写推理过程。
02
经历观察、猜想、推理、验证等过程,发展空间观念和逻辑推理能力,体会转化、类比等数学思想方法。
03
02
新知导入
几何语言
∵∠1=∠2
∴ AB∥ CD(同位角相等,两直线平行)
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;
再根据“同位角相等,两直线平行”推导出这两条直线平行.
思考
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a∥ b吗?
已知: ∠2=∠4
求证: a∥ b
还有隐藏条件吗?
03
新知探究
已知: ∠2=∠4
求证: a∥ b
证明:∵ ∠2=∠4
又∠1=∠2(对顶角相等)
∴∠1=∠4(等量代换)
∴ a∥ b (同位角相等,两直线平行)
03
新知探究
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(内错角相等,两直线平行)
03
新知探究
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
思考
如图,直线a,b被直线c所截,如果同旁内角∠3和∠4互补,你能根据判断方法1、2,说明直线a∥ b吗?
已知: ∠3+∠4=180°
求证: a∥ b
还有隐藏条件吗?
03
新知探究
已知: ∠3+∠4=180°
求证: a∥ b
证明:∵ ∠3+∠4=180°
又∠1+∠3=180°
∴∠4=∠1
∴ a∥ b (同位角相等,两直线平行)
判定方法1
03
新知探究
已知: ∠3+∠4=180°
求证: a∥ b
证明:∵ ∠3+∠4=180°
又∠2+∠3=180°
∴∠4=∠2
∴ a∥ b (内错角相等,两直线平行)
判定方法2
03
新知探究
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
几何语言
∵∠1+∠2=180°
∴ AB∥ CD(同旁内角互补,两直线平行)
03
新知探究
利用同旁内角互补来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.
04
课堂练习
【知识技能类作业】必做题:
1.如图,下列条件能判定AD∥ BC的是( )
A.∠D=∠EAD
B.∠C+∠D=180°
C.∠B=∠D
D.∠B=∠C
B
04
课堂练习
【知识技能类作业】必做题:
2.如图,下列能判定AD∥BC的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4 ;④∠B=∠5;⑤∠D=∠5
A.1个 B.2个 C.3个 D.4个
C
04
课堂练习
【知识技能类作业】必做题:
3.如图,已知a,b,c,d四条直线,下列不能判断a∥ b的是( )
A.∠2=∠3
B.∠4=∠5
C.∠1+∠4=180°
D.∠1+∠3=180°
C
04
课堂练习
【知识技能类作业】选做题:
4.如图,已知∠1=60°,当∠2= °时,a∥ b.
60
04
课堂练习
【知识技能类作业】选做题:
5.如图,一个弯形管道ABCD.若它的两个拐角∠B=110°,∠C=70°,则管道AB∥CD.推理依据是 .
同旁内角互补,两直线平行
04
课堂练习
【知识技能类作业】选做题:
6.如图,∠1=∠2,再加一个条件使得DE∥ BC,且EF∥ BD,你添加的条件是 .
∠BDE=∠1(答案不唯一)
04
课堂练习
【综合拓展类作业】
7.如下图,已知F,E分别是射线AB,CD上的点.连接AC,AE平分∠BAC,∠2=∠3,试说明:AB∥ CD.
解:∵AE平分∠BAC,
∴∠1=∠2.
∵∠2=∠3,
∴∠1=∠3,
∴ AB∥ CD(内错角相等,两直线平行) .
05
课堂小结
判定两直线平行的方法
1. 直线的位置关系:
(1)同一平面内不相交的两条直线平行 .
(2)同平行于第三条直线的两条直线平行 .
2. 角的大小关系:同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
06
作业布置
【知识技能类作业】
1.如图,下列条件不能判定CF∥BE的是( )
A.∠1=∠B
B.∠1=∠C
C.∠CFB+∠B=180°
D.∠CFP=∠FPB
B
06
作业布置
【知识技能类作业】
2.如图,下列条件中,不能判断直线a∥ b的是( )
A.∠1=∠3
B.∠2=∠3
C.∠4=∠5
D.∠2+∠4=180°
B
06
作业布置
【知识技能类作业】
3.如图,有以下条件:①∠1=∠2;②∠3=∠4;③∠1+∠3+∠BGC=180°;④∠1+∠3=∠2+∠4;⑤∠E=∠F,∠1=∠2.其中能判断AB∥ CD的条件有
(填序号).
③④⑤
06
作业布置
【综合拓展类作业】
4.如图,已知点C、B分别在线段AE、DF上,∠1=∠2,∠A=∠D.求证:AE∥ DF.
证明:∵∠1=∠2,
∴CD∥ AB,
∴∠D+∠ABD=180°,
∵∠A=∠D,
∴∠A+∠ABD=180°,
∴AE∥ DF(同旁内角互补,两直线平行).
07
板书设计
判断方法2:
几何语言:
判断方法3:
几何语言:
10.2.4 平行线的判定方法2、3
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
