沪科版七下(2024版)10.2.3 平行线的判定方法1 课件
文档属性
| 名称 | 沪科版七下(2024版)10.2.3 平行线的判定方法1 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 14:39:31 | ||
图片预览




文档简介
(共27张PPT)
第10章 相交线、平行线与平移
10.2.3 平行线的判定方法1
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解“同位角相等,两直线平行”的判定方法,能运用其判断两直线是否平行,并规范书写推理过程 。
01
能用尺规作图:过直线外一点作这条直线的平行线。
02
通过实验操作、观察分析、逻辑推理等活动,发展空间观念和几何推理能力。
03
02
新知导入
平行公理:
过直线外一点有且只有一条直线与这条直线平行.
平行公理的推论:
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
02
新知导入
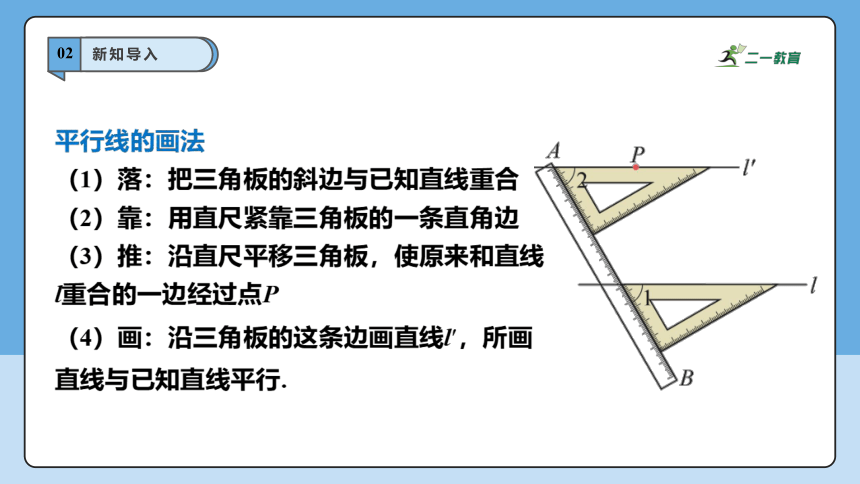
平行线的画法
(1)落:把三角板的斜边与已知直线重合
(2)靠:用直尺紧靠三角板的一条直角边
(3)推:沿直尺平移三角板,使原来和直线l重合的一边经过点P
(4)画:沿三角板的这条边画直线l,所画直线与已知直线平行.
观察
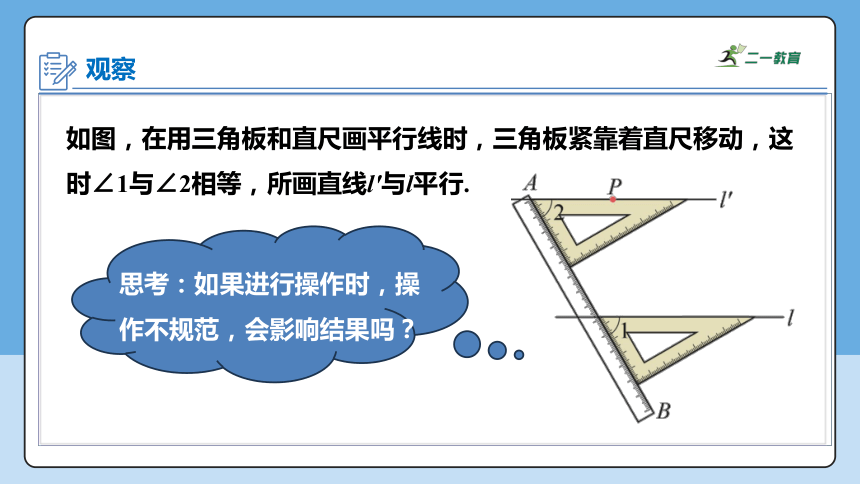
如图,在用三角板和直尺画平行线时,三角板紧靠着直尺移动,这时∠1与∠2相等,所画直线l'与l平行.
思考:如果进行操作时,操作不规范,会影响结果吗?
观察
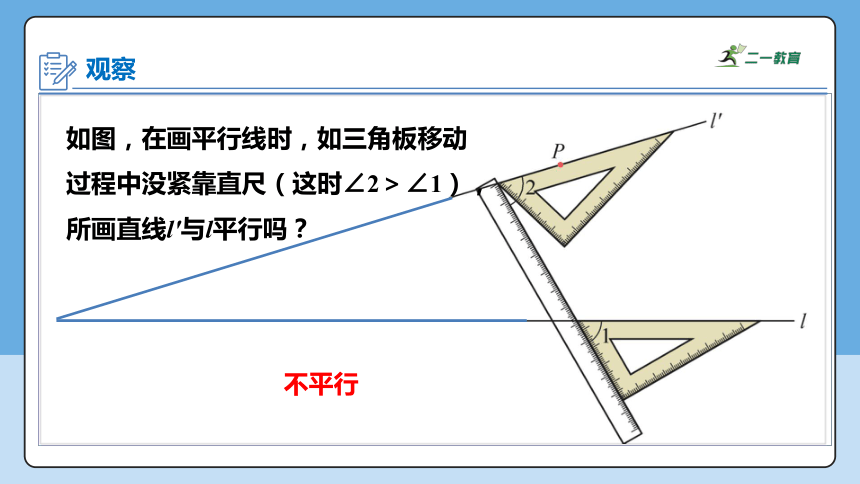
如图,在画平行线时,如三角板移动过程中没紧靠直尺(这时∠2>∠1),所画直线l'与l平行吗?
不平行
观察
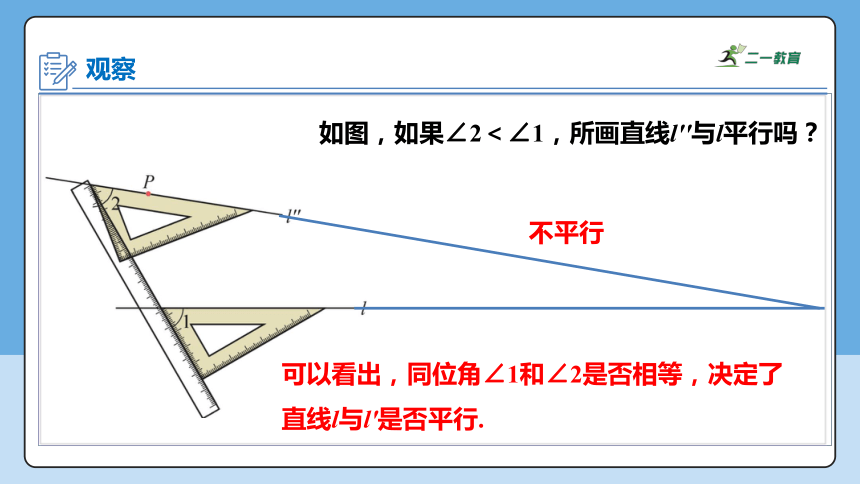
如图,如果∠2<∠1,所画直线l''与l平行吗?
不平行
可以看出,同位角∠1和∠2是否相等,决定了直线l与l'是否平行.
03
新知探究
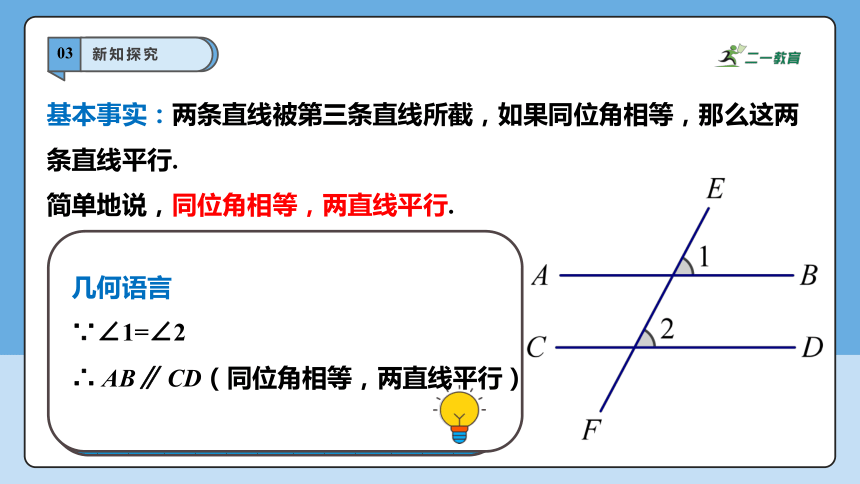
基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(同位角相等,两直线平行)
03
新知探究
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;
再根据“同位角相等,两直线平行”推导出这两条直线平行.
03
新知探究
例2
已知:直线 和点 ,点 在直线 外,求作:直线 ,使直线 ∥ .
分析:根据“同位角相等,两直线平行”,可将作平行线的问题转化为作角相等的问题.因此,过点C作一条直线与AB相交(作截线),然后作一对同位角相等即可.
03
新知探究
例2
已知:直线 和点 ,点 在直线 外,求作:直线 ,使直线 ∥ .
作法 1.如图,过点C作直线EF交AB于点F.
2.以点C为顶点,CE为边,在EF的右侧作∠ECD=∠EFB.
3.作直线CD.
直线CD就是所求作的直线.
04
课堂练习
【知识技能类作业】必做题:
1.下列图形中,由∠1=∠2能判定AB∥ CD的是( )
C
A
B
C
D
04
课堂练习
2.如图,∠ABC=45°,∠EDF=60°,若要使直线BC∥EG,则可使直线EG绕点D逆时针旋转( )
A.15°
B.25°
C.30°
D.105°
A
04
课堂练习
3.如图所示,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
A
04
课堂练习
【知识技能类作业】选做题:
4.如图:∵ ,∴AB∥CD(填写一个满足条件的理由,用符号表示,不得添加任何辅助线).
∠ABE=∠C
04
课堂练习
5.某学员在练车场练习开小轿车,第一次向左拐弯30°行驶一段后,第二次向右拐弯30°,如图.经过两次拐弯后行驶的方向与原来行驶的方向 (填“平行”或“不平行”).
平行
04
课堂练习
6.如图,已知点A、B、C和点D、E、F分别在同一直线上,∠1=∠2,那么 ∥ .
BD
CE
04
课堂练习
【综合拓展类作业】
7.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断DG和AB的位置关系,并说明理由.
解:DG//AB,理由如下:
因为CE⊥DG,
所以∠ECG=90°.
因为∠ACE=140°,
所以∠ACG=∠ACE-∠ECG=50°.
又因为∠BAF=50°,
所以∠BAF=∠ACG,
所以AB//DG(同位角相等,两直线平行).
05
课堂小结
判定两直线平行的方法
1. 直线的位置关系:
(1)同一平面内不相交的两条直线平行 .
(2)同平行于第三条直线的两条直线平行 .
2. 角的大小关系:同位角相等,两直线平行.
06
作业布置
【知识技能类作业】
1.如图,∠1=∠2,则下列结论正确的是( )
A.AD//BC
B.AB//CD
C.AD//EF
D.EF//BC
C
06
作业布置
2.如图,已知直线a,b,c.若∠1=∠2=40° ,且∠2=∠3,则图中平行线的组数为( )
A.0
B.1
C.2
D.3
D
06
作业布置
3.请把下列解题过程补充完整并在括号中注明理由.
如图,点C,D,E在同一直线上.
因为∠1=130° (已知),
所以∠2=_______(补角的定义).
因为∠3=50°(已知),
所以∠2=_________(等量代换).
所以______ //_______(同位角相等,两直线平行).
50°
∠3
AD
CF
06
作业布置
【综合拓展类作业】
4.如图,在三角形ABC中,AD⊥BC,垂足为D,∠B+∠C=90°,∠ADE=∠C.求证:DE∥ AB.
证明:∵AD⊥BC,
∴∠ADE+∠EDC=90°(垂直的定义).
∵∠B+∠C=90°,∠ADE=∠C.
∴∠B+∠ADE=90°(等量代换).
∴∠B=∠EDC(同角的余角相等).
∴DE∥ AB(同位角相等,两直线平行).
07
板书设计
基本事实:
尺规作图:
10.2.3 平行线的判定方法1
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第10章 相交线、平行线与平移
10.2.3 平行线的判定方法1
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解“同位角相等,两直线平行”的判定方法,能运用其判断两直线是否平行,并规范书写推理过程 。
01
能用尺规作图:过直线外一点作这条直线的平行线。
02
通过实验操作、观察分析、逻辑推理等活动,发展空间观念和几何推理能力。
03
02
新知导入
平行公理:
过直线外一点有且只有一条直线与这条直线平行.
平行公理的推论:
平行于同一条直线的两条直线平行.
如果a∥b,c∥b,那么a∥c.
02
新知导入
平行线的画法
(1)落:把三角板的斜边与已知直线重合
(2)靠:用直尺紧靠三角板的一条直角边
(3)推:沿直尺平移三角板,使原来和直线l重合的一边经过点P
(4)画:沿三角板的这条边画直线l,所画直线与已知直线平行.
观察
如图,在用三角板和直尺画平行线时,三角板紧靠着直尺移动,这时∠1与∠2相等,所画直线l'与l平行.
思考:如果进行操作时,操作不规范,会影响结果吗?
观察
如图,在画平行线时,如三角板移动过程中没紧靠直尺(这时∠2>∠1),所画直线l'与l平行吗?
不平行
观察
如图,如果∠2<∠1,所画直线l''与l平行吗?
不平行
可以看出,同位角∠1和∠2是否相等,决定了直线l与l'是否平行.
03
新知探究
基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
几何语言
∵∠1=∠2
∴ AB∥ CD(同位角相等,两直线平行)
03
新知探究
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;
再根据“同位角相等,两直线平行”推导出这两条直线平行.
03
新知探究
例2
已知:直线 和点 ,点 在直线 外,求作:直线 ,使直线 ∥ .
分析:根据“同位角相等,两直线平行”,可将作平行线的问题转化为作角相等的问题.因此,过点C作一条直线与AB相交(作截线),然后作一对同位角相等即可.
03
新知探究
例2
已知:直线 和点 ,点 在直线 外,求作:直线 ,使直线 ∥ .
作法 1.如图,过点C作直线EF交AB于点F.
2.以点C为顶点,CE为边,在EF的右侧作∠ECD=∠EFB.
3.作直线CD.
直线CD就是所求作的直线.
04
课堂练习
【知识技能类作业】必做题:
1.下列图形中,由∠1=∠2能判定AB∥ CD的是( )
C
A
B
C
D
04
课堂练习
2.如图,∠ABC=45°,∠EDF=60°,若要使直线BC∥EG,则可使直线EG绕点D逆时针旋转( )
A.15°
B.25°
C.30°
D.105°
A
04
课堂练习
3.如图所示,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
A
04
课堂练习
【知识技能类作业】选做题:
4.如图:∵ ,∴AB∥CD(填写一个满足条件的理由,用符号表示,不得添加任何辅助线).
∠ABE=∠C
04
课堂练习
5.某学员在练车场练习开小轿车,第一次向左拐弯30°行驶一段后,第二次向右拐弯30°,如图.经过两次拐弯后行驶的方向与原来行驶的方向 (填“平行”或“不平行”).
平行
04
课堂练习
6.如图,已知点A、B、C和点D、E、F分别在同一直线上,∠1=∠2,那么 ∥ .
BD
CE
04
课堂练习
【综合拓展类作业】
7.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断DG和AB的位置关系,并说明理由.
解:DG//AB,理由如下:
因为CE⊥DG,
所以∠ECG=90°.
因为∠ACE=140°,
所以∠ACG=∠ACE-∠ECG=50°.
又因为∠BAF=50°,
所以∠BAF=∠ACG,
所以AB//DG(同位角相等,两直线平行).
05
课堂小结
判定两直线平行的方法
1. 直线的位置关系:
(1)同一平面内不相交的两条直线平行 .
(2)同平行于第三条直线的两条直线平行 .
2. 角的大小关系:同位角相等,两直线平行.
06
作业布置
【知识技能类作业】
1.如图,∠1=∠2,则下列结论正确的是( )
A.AD//BC
B.AB//CD
C.AD//EF
D.EF//BC
C
06
作业布置
2.如图,已知直线a,b,c.若∠1=∠2=40° ,且∠2=∠3,则图中平行线的组数为( )
A.0
B.1
C.2
D.3
D
06
作业布置
3.请把下列解题过程补充完整并在括号中注明理由.
如图,点C,D,E在同一直线上.
因为∠1=130° (已知),
所以∠2=_______(补角的定义).
因为∠3=50°(已知),
所以∠2=_________(等量代换).
所以______ //_______(同位角相等,两直线平行).
50°
∠3
AD
CF
06
作业布置
【综合拓展类作业】
4.如图,在三角形ABC中,AD⊥BC,垂足为D,∠B+∠C=90°,∠ADE=∠C.求证:DE∥ AB.
证明:∵AD⊥BC,
∴∠ADE+∠EDC=90°(垂直的定义).
∵∠B+∠C=90°,∠ADE=∠C.
∴∠B+∠ADE=90°(等量代换).
∴∠B=∠EDC(同角的余角相等).
∴DE∥ AB(同位角相等,两直线平行).
07
板书设计
基本事实:
尺规作图:
10.2.3 平行线的判定方法1
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
