10.5用二元一次方程组解决问题同步强化练习(含解析)
文档属性
| 名称 | 10.5用二元一次方程组解决问题同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 632.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 07:25:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
10.5用二元一次方程组解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.国家“双减”政策实施后,某校开展了丰富多彩的社团活动.某班同学报名参加书法和围棋两个社团,班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费360元.其中毛笔每支15元,围棋每副20元,共有多少种购买方案?( )
A.5 B.6 C.7 D.8
2.《九章算术》中记载这样一个问题:“以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.问绳长、井深各几何?”题意是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设绳长、井深分别为x、y尺,则符合题意的方程组是( )
A. B. C. D.
3.春节前夕,某旅游景区的成人票和学生票均打折,李凯同学一家(个成人和个学生)去了该景区,门票共花费元,王玲同学一家(个成人和个学生)去了该景区,门票共花费元,则赵芸同学和妈妈去该景区游玩时,门票需要花费( )
A.元 B.元 C.元 D.元
4.将8个一样大小的长方形,恰好可以拼成一个大的长方形如图1,将这8个一样大小的长方形拼成了如图2那样的正方形,中间还留了一个洞,恰好是边长为2cm的小正方形,则一个小长方形的面积为( )
A. B. C. D.
5.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
6.某车间有工人54人,每人平均每天可加工轴杆15个或轴承24个,一个轴杆与两个轴承配成一套.若分配x个工人加工轴杆,y个工人加工轴承,正好使每天加工的产品成套,则可列方程组为( ).
A. B.
C. D.
7.打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花( )
A.200元 B.300元 C.400元 D.500元
8.宁波市出租车起步价所包含的路程为,超过的部分按每千米另收费.小明乘坐这种出租车走了,付了元;小红乘坐这种出租车走了,付了元.设这种出租车的起步价为x元,超过后每千米收费y元,则下列方程组正确的是( )
A. B. C. D.
9.我国古代《算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中.一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设有客房间,客人人,则可列方程组为( )
A. B. C. D.
10.我国古代数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊三,直金十二两.问牛、羊各直金几何?”题目大意是:5头牛、2只羊共19两银子;2头牛、3只羊共12两银子,每头牛、每只羊各多少两银子?设1头牛两银子,1只羊两银子,则可列方程组为( )
A. B. C. D.
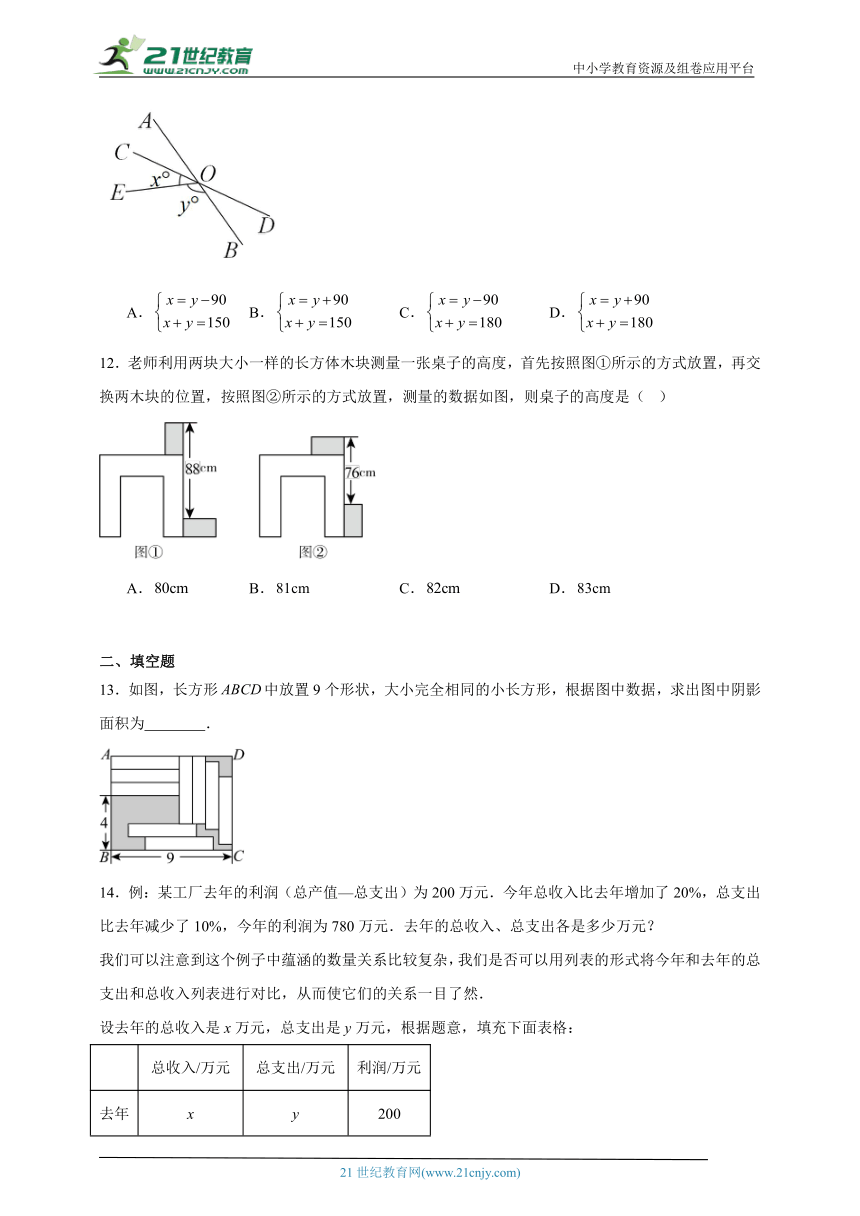
11.如图,直线AB与CD相交于点O,且∠AOD=150°.∠EOB比∠COE大90°,设∠COE=x°,∠EOB=y°,则可得到的方程组为( )
A. B. C. D.
12.老师利用两块大小一样的长方体木块测量一张桌子的高度,首先按照图①所示的方式放置,再交换两木块的位置,按照图②所示的方式放置,测量的数据如图,则桌子的高度是( )
A. B. C. D.
二、填空题
13.如图,长方形中放置9个形状,大小完全相同的小长方形,根据图中数据,求出图中阴影面积为 .
14.例:某工厂去年的利润(总产值—总支出)为200万元.今年总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总收入、总支出各是多少万元?
我们可以注意到这个例子中蕴涵的数量关系比较复杂,我们是否可以用列表的形式将今年和去年的总支出和总收入列表进行对比,从而使它们的关系一目了然.
设去年的总收入是x万元,总支出是y万元,根据题意,填充下面表格:
总收入/万元 总支出/万元 利润/万元
去年 x y 200
今年 (1+20%)x (1-10%)y 780
根据上表,可以列出方程组 ,
解得 .
因此,去年的总收入是万元 ,总支出是 万元.
15.两组工人按计划本月应共生产680个零件,实际第一组超额、第二组超额完成了本月任务,因此比原计划多生产118个零件,则本月原计划第一组生产 个零件、第二组生产 个零件.
16.4辆小卡车和5辆大卡车一次能运货,设每辆小卡车每次运货,每辆大卡车每次运货.
①列出关于x,y的二元一次方程: .
②已知,则 .
③若每辆大卡车每次运货,则每辆小卡车每次运货 t.
17.小明家种植水果,去年收支相抵后,结余1 200元;今年因为改进了种植技术,他家水果获得丰收,收入比去年增加5%,支出比去年减少15%,今年比去年多结余1 140元.如果设小明家去年收入x元,支出为y元,那么:
(1)将有关的数据填写在下表中:
项目 收入(元) 支出(元) 结余
去年 x y 1 200
今年 2 340
(2)根据表格列方程组 ,解得 .
三、解答题
18.为了抓住中秋商机,某超市决定购进A,B两种月饼,若购进A种月饼10盒,B种月饼5盒,需要600元:若购进A种月饼5盒,B种月饼3盒,需要330元,该超市决定拿出6000元全部用来购进两种月饼,考虑市场需求,要求购进A种月饼的数量不少于B种月饼数量6倍,且不超过B种月饼数量的8倍.若销售每盒A种月饼可获利20元,销售每盒B种月饼可获利30元,怎样设计进货方案才能使得获利最大?最大利润是多少元?
19.安居小区业主安先生准备装修新居,装修公司派来甲工程队完成此项工程.由于工期过长,安先生要求装修公司再派乙工程队与甲队共同工作.已知甲工程队单独完成此项工程需要的天数恰好比乙工程队单独完成此项工程需要的天数的3倍少5天,并且甲工程队单独完成此项工程需要的天数与乙工程队单独完成此项工程需要的天数之和为55天.
(1)求甲、乙两队单独完成此项工程各需要多少天;
(2)若甲工程队工作10天后,与公司派来的乙工程队再合作多少天可完成此项工程的.
20.学校组织春游,每人车费4元.下面是一班的班长小明与二班的班长小红的对话.
小明:我们两班共93人.
小红:我们二班比你们一班多交了12元的车费.
根据上面对话,求一班和二班各有多少人.
21.《孙子算经》是中国古代最重要的数学著作,约成书于四、五世纪,其中记载:“今有木,不知长短.引绳度之,余绳五尺五寸,屈绳量之,不足一尺,木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余5.5尺,将绳子对折再量长木,长木还剩余1尺,问木长多少尺?
22.某校要购置规格分别为/瓶和/瓶的甲、乙两种洗手液若干瓶,已知购买3瓶甲种洗手液和1瓶乙种洗手液需要84元,购买2瓶甲种洗手液和3瓶乙种洗手液需要126元.
(1)求甲、乙两种洗手液的单价.
(2)七年级师生共有2000人,平均每人每天都需使用的洗手液.若七年级采购甲、乙两种洗手液共花费了7200元,则这批洗手液可使用多少天?
23.小明、小丽一起去文具店购买学习用品,根据他们的对话,求出1本笔记本和1支水笔的价格.
小明:“我买了1本笔记本和4支水笔,共花了18元.”
小丽:“我买了1本笔记本和1支水笔,刚好花了6元.”
24.2024年4月13日,以“共享开放机遇、共创美好生活”为主题的第四届中国国际消费品博览会在海南海口开幕,吉祥物“元元”和“宵宵”深受大家的喜欢,某供应商购进一批“元元”和“宵宵”,已知一个“元元”的进价比一个“宵宵”的进价多20元,并且购买4个“元元”的价格是购买3个“宵宵”价格的2倍.某供应商购进每个“元元”和“宵宵”的进价分别是多少元?
《10.5用二元一次方程组解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B A B C D D A
题号 11 12
答案 A C
1.A
【分析】设设购买毛笔x支,围棋y副,根据总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出购买方案的数量.
【详解】解:设购买毛笔x支,围棋y副,根据题意得,
15x+20y=360,即3x+4y=72,
∴y=18-x.
又∵x,y均为正整数,
∴或或或或,
∴班长有5种购买方案.
故选:A.
【点睛】本题考查了二元一次方程的应用,找准等量关系“共花费360元”,列出二元一次方程是解题的关键.
2.C
【分析】设绳长为x尺,根据水井的深度不变,得出关于x的一元一次方程即可解答.
【详解】解:若设绳长、井深分别为x、y尺,
则符合题意的方程组是,
故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题关键.
3.A
【分析】设成人票是元张,学生票是元张,根据“李凯同学一家个成人和个学生去了该景区,门票共花费元,王玲同学一家个成人和个学生去了该景区,门票共花费元”列出方程组,求得的值即可.
【详解】解:设成人票是元张,学生票是元张,
依题意得:
,
②①得:.
即赵芸同学和妈妈去该景区游玩时,门票需要花费元.
故选:A.
【点睛】本题考查了二元一次方程组的应用.此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可.
4.B
【分析】本题主要考查二元一次方程组的应用,根据题意列出方程组,并求得其解,即可求得小长方形的面积.
【详解】解:设小长方形的长为,宽为,根据题意得:
,解得,
∴.
故选:B.
5.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
6.B
【分析】本题考查了列二元一次方程组,设分配x个工人生产轴杆,y个工人生产轴承,则生产轴杆个,生产轴承个,根据一个轴杆和两个轴承配成一套建立方程即可.
【详解】解:设分配x个工人生产轴杆,y个工人生产轴承,根据题意得
故选:B.
7.C
【分析】此题考查了二元一次方程组的应用,设打折前每件A商品x元,每件B商品y元,根据“买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元”列出方程组,解方程组后进一步计算即可得到答案.
【详解】解:设打折前每件A商品x元,每件B商品y元,
∵买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,
∴,
解得,
∴打折前每件A商品16元,每件B商品4元,
∵(元),
∴买500件A商品和500件B商品比不打折少花400元;
故选:C.
8.D
【分析】设这种出租车的起步价为x元,超过后每千米收费y元,由题意得等量关系:①起步价x元+超过后的费用=23元;②起步价x元+超过后的费用=35元,再列出方程组即可.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,
由题意得:.
故选:D.
【点睛】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.
9.D
【分析】本题考查的是二元一次方程组的应用,设有客房间,客人人,根据每一间客房住7人,则有7人无房可住;每一间客房住9人,则就空出一间客房,再建立方程组解题即可.
【详解】解:如果每一间客房住7人,那么有7人无房可住,
.
如果每一间客房住9人,那么就空出一间客房,
.
根据题意可列方程组,
故选D.
10.A
【分析】根据“5头牛、2只羊共19两银子;2头牛、3只羊共12两银子”,得到两个等量关系,即可列出方程组.
【详解】解:设1头牛两银子,1只羊两银子,
由题意可得:,
故选:A.
【点睛】本题考查由实际问题抽象初二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
11.A
【分析】根据“∠AOD=150°,∠EOB比∠COE大90°”即可得出关于x、y的二元一次方程组.
【详解】解:∵∠AOD=150°,
∴∠COE+∠EOB=∠BOC=∠AOD=150°,
由题意可得:.
故选:A.
【点睛】本题考查对顶角相等和由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,找到等量关系,列出相应的方程组.
12.C
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.设桌子的高度为,长方体木块一个面(图中展示的面)的长比宽大,根据图中两种放置的方式,列出二元一次方程组,解之即可得出结论.
【详解】解:设桌子的高度为,长方体木块一个面(图中展示的面)的长比宽大,
由题意得:,
解得:,
∴桌子的高度为,
故选:C.
13.18
【分析】本题考查了二元一次方程组的应用,设每个小长方形的长为x,宽为y,根据题意,得,结合计算即可.
【详解】设每个小长方形的长为x,宽为y,根据题意,得
,
解得
故,
故答案为:18.
14. , , 2000, 1800,
【解析】略
15. 320 360
【分析】本题考查了二元一次方程的应用,理解题意并正确列方程是解题关键.设原计划第一组生产个零件、第二组生产个零件,根据题意列二元一次方程求解即可.
【详解】解:设原计划第一组生产个零件、第二组生产个零件,
则,
解得:,
即原计划第一组生产个零件、第二组生产个零件,
故答案为:320;360.
16. 5 3
【分析】本题考查二元一次方程的解,首先根据题意列出二元一次方程,然后根据题目提供的条件进行求解.
【详解】解:①列出关于x,y的二元一次方程: ;
②当时,则,解得:;
③当时,则,解得:;
故答案为:;5;3.
17. (1) (1+5%)x, (1-15%)y (2),
【解析】略
18.该超市购进种月饼160盒,购进种月饼20盒才能使得获利最大,最大利润是3800元
【分析】设种月饼每盒元,种月饼每盒元,根据两种购买方式建立方程组,解方程组可得的值,再设该超市购进种月饼盒,可获得的利润为元,则该超市购进种月饼盒,从而可得,然后根据两种月饼数量的关系建立不等式组,解不等式组求出的取值范围,从而可得的取值范围,由此即可得.
【详解】解:设种月饼每盒元,种月饼每盒元,
由题意得:,
解得,
即种月饼每盒30元,种月饼每盒60元,
设该超市购进种月饼盒,可获得的利润为元,则该超市购进种月饼盒,
由题意得:,
要求购进种月饼的数量不少于种月饼数量6倍,且不超过B种月饼数量的8倍,
,
解得,
,即,
则当时,取得最大值,最大值为3800,
此时,
答:该超市购进种月饼160盒,购进种月饼20盒才能使得获利最大,最大利润是3800元.
【点睛】本题考查了二元一次方程组的应用、一元一次不等式组的应用,正确建立方程组和不等式组是解题关键.
19.(1)甲队单独完成此项工程需要40天,乙队单独完成此项工程需要15天
(2)与公司派来的乙工程队再合作6天可完成此项工程
【分析】本题考查了一元一次方程的应用,二元一次方程组的应用.解题的关键在于根据题意正确的列方程(组).
(1)设甲队单独完成此项工程需要天,乙队单独完成此项工程需要天,根据题意列出方程组,解方程组,即可求解;
(2)设与公司派来的乙工程队再合作天可完成此项工程的,根据题意列出一元一次方程,解方程,即可求解.
【详解】(1)解:设甲队单独完成此项工程需要天,乙队单独完成此项工程需要天,
根据题意得
解得
答:甲队单独完成此项工程需要40天,乙队单独完成此项工程需要15天
(2)解:设与公司派来的乙工程队再合作天可完成此项工程的,
根据题意得,
解得,
答:与公司派来的乙工程队再合作6天可完成此项工程.
20.一班45人,二班48人
【分析】设一班x人,二班y人,根据“两班共93人”和“二班比你们一班多交了12元的车费.”列出方程组,解方程组即可.
【详解】解:设一班x人,二班y人,
则 ,
解得:,
即一班45人,二班48人.
答:一班45人,二班48人.
【点睛】此题考查了二元一次方程组的实际应用,读懂题意,找出等量关系列出方程组是解题的关键.
21.7.5尺
【分析】本题考查了二元一次方程组的应用以及数学常识,设绳子长x尺,长木长y尺,根据“用一根绳子去量一根长木,绳子还剩余5.5尺,将绳子对折再量长木,长木还剩余1尺”,可得出关于x,y的二元一次方程组,解方程组即可.
【详解】解:设绳子长x尺,长木长y尺,
依题意,得:,
解得,
答:木长7.5尺.
22.(1)甲、乙两种洗手液的单价分别为18元/瓶,30元/瓶
(2)6天
【分析】本题主要考查二元一次方程组的应用,解题的关键是理解题意;
(1)设甲种洗手液的单价为x元,乙种洗手液的单价为y元,由题意可得方程组,解方程组即可得解;
(2)设七年级采购甲、乙两种洗手液各m瓶,n瓶,由题意易得,然后进行求解即可.
【详解】(1)解:设甲种洗手液的单价为x元/瓶,乙种洗手液的单价为y元/瓶,由题意得:
,
解得:,
答:甲、乙两种洗手液的单价分别为18元/瓶,30元/瓶.
(2)解:设七年级采购甲、乙两种洗手液各m瓶,n瓶,由题意得:
,
∴,
∴(天);
答:这批洗手液可使用6天.
23.买1本笔记本需要2元,1支水笔需要4元
【分析】本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.
设买1本笔记本需要元,1支水笔需要元,根据买1本笔记本和4支水笔,共花了18元和买1本笔记本和1支水笔,刚好花了6元,列出二元一次方程组,解方程组即可.
【详解】解:设买1本笔记本需要元,1支水笔需要元,
根据题意,得,
解得;
答:买1本笔记本需要2元,1支水笔需要4元.
24.供应商购进每个“元元”和“宵宵”的进价分别是60元,40元
【分析】本题主要考查了二元一次方程组的实际应用,设供应商购进每个“元元”和“宵宵”的进价分别是x元,y元,根据一个“元元”的进价比一个“宵宵”的进价多20元,并且购买4个“元元”的价格是购买3个“宵宵”价格的2倍列出方程组求解即可.
【详解】解:设供应商购进每个“元元”和“宵宵”的进价分别是x元,y元,
由题意得,,
解得,
答:供应商购进每个“元元”和“宵宵”的进价分别是60元,40元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
10.5用二元一次方程组解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.国家“双减”政策实施后,某校开展了丰富多彩的社团活动.某班同学报名参加书法和围棋两个社团,班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费360元.其中毛笔每支15元,围棋每副20元,共有多少种购买方案?( )
A.5 B.6 C.7 D.8
2.《九章算术》中记载这样一个问题:“以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.问绳长、井深各几何?”题意是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设绳长、井深分别为x、y尺,则符合题意的方程组是( )
A. B. C. D.
3.春节前夕,某旅游景区的成人票和学生票均打折,李凯同学一家(个成人和个学生)去了该景区,门票共花费元,王玲同学一家(个成人和个学生)去了该景区,门票共花费元,则赵芸同学和妈妈去该景区游玩时,门票需要花费( )
A.元 B.元 C.元 D.元
4.将8个一样大小的长方形,恰好可以拼成一个大的长方形如图1,将这8个一样大小的长方形拼成了如图2那样的正方形,中间还留了一个洞,恰好是边长为2cm的小正方形,则一个小长方形的面积为( )
A. B. C. D.
5.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
6.某车间有工人54人,每人平均每天可加工轴杆15个或轴承24个,一个轴杆与两个轴承配成一套.若分配x个工人加工轴杆,y个工人加工轴承,正好使每天加工的产品成套,则可列方程组为( ).
A. B.
C. D.
7.打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花( )
A.200元 B.300元 C.400元 D.500元
8.宁波市出租车起步价所包含的路程为,超过的部分按每千米另收费.小明乘坐这种出租车走了,付了元;小红乘坐这种出租车走了,付了元.设这种出租车的起步价为x元,超过后每千米收费y元,则下列方程组正确的是( )
A. B. C. D.
9.我国古代《算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中.一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设有客房间,客人人,则可列方程组为( )
A. B. C. D.
10.我国古代数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊三,直金十二两.问牛、羊各直金几何?”题目大意是:5头牛、2只羊共19两银子;2头牛、3只羊共12两银子,每头牛、每只羊各多少两银子?设1头牛两银子,1只羊两银子,则可列方程组为( )
A. B. C. D.
11.如图,直线AB与CD相交于点O,且∠AOD=150°.∠EOB比∠COE大90°,设∠COE=x°,∠EOB=y°,则可得到的方程组为( )
A. B. C. D.
12.老师利用两块大小一样的长方体木块测量一张桌子的高度,首先按照图①所示的方式放置,再交换两木块的位置,按照图②所示的方式放置,测量的数据如图,则桌子的高度是( )
A. B. C. D.
二、填空题
13.如图,长方形中放置9个形状,大小完全相同的小长方形,根据图中数据,求出图中阴影面积为 .
14.例:某工厂去年的利润(总产值—总支出)为200万元.今年总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总收入、总支出各是多少万元?
我们可以注意到这个例子中蕴涵的数量关系比较复杂,我们是否可以用列表的形式将今年和去年的总支出和总收入列表进行对比,从而使它们的关系一目了然.
设去年的总收入是x万元,总支出是y万元,根据题意,填充下面表格:
总收入/万元 总支出/万元 利润/万元
去年 x y 200
今年 (1+20%)x (1-10%)y 780
根据上表,可以列出方程组 ,
解得 .
因此,去年的总收入是万元 ,总支出是 万元.
15.两组工人按计划本月应共生产680个零件,实际第一组超额、第二组超额完成了本月任务,因此比原计划多生产118个零件,则本月原计划第一组生产 个零件、第二组生产 个零件.
16.4辆小卡车和5辆大卡车一次能运货,设每辆小卡车每次运货,每辆大卡车每次运货.
①列出关于x,y的二元一次方程: .
②已知,则 .
③若每辆大卡车每次运货,则每辆小卡车每次运货 t.
17.小明家种植水果,去年收支相抵后,结余1 200元;今年因为改进了种植技术,他家水果获得丰收,收入比去年增加5%,支出比去年减少15%,今年比去年多结余1 140元.如果设小明家去年收入x元,支出为y元,那么:
(1)将有关的数据填写在下表中:
项目 收入(元) 支出(元) 结余
去年 x y 1 200
今年 2 340
(2)根据表格列方程组 ,解得 .
三、解答题
18.为了抓住中秋商机,某超市决定购进A,B两种月饼,若购进A种月饼10盒,B种月饼5盒,需要600元:若购进A种月饼5盒,B种月饼3盒,需要330元,该超市决定拿出6000元全部用来购进两种月饼,考虑市场需求,要求购进A种月饼的数量不少于B种月饼数量6倍,且不超过B种月饼数量的8倍.若销售每盒A种月饼可获利20元,销售每盒B种月饼可获利30元,怎样设计进货方案才能使得获利最大?最大利润是多少元?
19.安居小区业主安先生准备装修新居,装修公司派来甲工程队完成此项工程.由于工期过长,安先生要求装修公司再派乙工程队与甲队共同工作.已知甲工程队单独完成此项工程需要的天数恰好比乙工程队单独完成此项工程需要的天数的3倍少5天,并且甲工程队单独完成此项工程需要的天数与乙工程队单独完成此项工程需要的天数之和为55天.
(1)求甲、乙两队单独完成此项工程各需要多少天;
(2)若甲工程队工作10天后,与公司派来的乙工程队再合作多少天可完成此项工程的.
20.学校组织春游,每人车费4元.下面是一班的班长小明与二班的班长小红的对话.
小明:我们两班共93人.
小红:我们二班比你们一班多交了12元的车费.
根据上面对话,求一班和二班各有多少人.
21.《孙子算经》是中国古代最重要的数学著作,约成书于四、五世纪,其中记载:“今有木,不知长短.引绳度之,余绳五尺五寸,屈绳量之,不足一尺,木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余5.5尺,将绳子对折再量长木,长木还剩余1尺,问木长多少尺?
22.某校要购置规格分别为/瓶和/瓶的甲、乙两种洗手液若干瓶,已知购买3瓶甲种洗手液和1瓶乙种洗手液需要84元,购买2瓶甲种洗手液和3瓶乙种洗手液需要126元.
(1)求甲、乙两种洗手液的单价.
(2)七年级师生共有2000人,平均每人每天都需使用的洗手液.若七年级采购甲、乙两种洗手液共花费了7200元,则这批洗手液可使用多少天?
23.小明、小丽一起去文具店购买学习用品,根据他们的对话,求出1本笔记本和1支水笔的价格.
小明:“我买了1本笔记本和4支水笔,共花了18元.”
小丽:“我买了1本笔记本和1支水笔,刚好花了6元.”
24.2024年4月13日,以“共享开放机遇、共创美好生活”为主题的第四届中国国际消费品博览会在海南海口开幕,吉祥物“元元”和“宵宵”深受大家的喜欢,某供应商购进一批“元元”和“宵宵”,已知一个“元元”的进价比一个“宵宵”的进价多20元,并且购买4个“元元”的价格是购买3个“宵宵”价格的2倍.某供应商购进每个“元元”和“宵宵”的进价分别是多少元?
《10.5用二元一次方程组解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B A B C D D A
题号 11 12
答案 A C
1.A
【分析】设设购买毛笔x支,围棋y副,根据总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出购买方案的数量.
【详解】解:设购买毛笔x支,围棋y副,根据题意得,
15x+20y=360,即3x+4y=72,
∴y=18-x.
又∵x,y均为正整数,
∴或或或或,
∴班长有5种购买方案.
故选:A.
【点睛】本题考查了二元一次方程的应用,找准等量关系“共花费360元”,列出二元一次方程是解题的关键.
2.C
【分析】设绳长为x尺,根据水井的深度不变,得出关于x的一元一次方程即可解答.
【详解】解:若设绳长、井深分别为x、y尺,
则符合题意的方程组是,
故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题关键.
3.A
【分析】设成人票是元张,学生票是元张,根据“李凯同学一家个成人和个学生去了该景区,门票共花费元,王玲同学一家个成人和个学生去了该景区,门票共花费元”列出方程组,求得的值即可.
【详解】解:设成人票是元张,学生票是元张,
依题意得:
,
②①得:.
即赵芸同学和妈妈去该景区游玩时,门票需要花费元.
故选:A.
【点睛】本题考查了二元一次方程组的应用.此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可.
4.B
【分析】本题主要考查二元一次方程组的应用,根据题意列出方程组,并求得其解,即可求得小长方形的面积.
【详解】解:设小长方形的长为,宽为,根据题意得:
,解得,
∴.
故选:B.
5.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
6.B
【分析】本题考查了列二元一次方程组,设分配x个工人生产轴杆,y个工人生产轴承,则生产轴杆个,生产轴承个,根据一个轴杆和两个轴承配成一套建立方程即可.
【详解】解:设分配x个工人生产轴杆,y个工人生产轴承,根据题意得
故选:B.
7.C
【分析】此题考查了二元一次方程组的应用,设打折前每件A商品x元,每件B商品y元,根据“买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元”列出方程组,解方程组后进一步计算即可得到答案.
【详解】解:设打折前每件A商品x元,每件B商品y元,
∵买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,
∴,
解得,
∴打折前每件A商品16元,每件B商品4元,
∵(元),
∴买500件A商品和500件B商品比不打折少花400元;
故选:C.
8.D
【分析】设这种出租车的起步价为x元,超过后每千米收费y元,由题意得等量关系:①起步价x元+超过后的费用=23元;②起步价x元+超过后的费用=35元,再列出方程组即可.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,
由题意得:.
故选:D.
【点睛】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.
9.D
【分析】本题考查的是二元一次方程组的应用,设有客房间,客人人,根据每一间客房住7人,则有7人无房可住;每一间客房住9人,则就空出一间客房,再建立方程组解题即可.
【详解】解:如果每一间客房住7人,那么有7人无房可住,
.
如果每一间客房住9人,那么就空出一间客房,
.
根据题意可列方程组,
故选D.
10.A
【分析】根据“5头牛、2只羊共19两银子;2头牛、3只羊共12两银子”,得到两个等量关系,即可列出方程组.
【详解】解:设1头牛两银子,1只羊两银子,
由题意可得:,
故选:A.
【点睛】本题考查由实际问题抽象初二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
11.A
【分析】根据“∠AOD=150°,∠EOB比∠COE大90°”即可得出关于x、y的二元一次方程组.
【详解】解:∵∠AOD=150°,
∴∠COE+∠EOB=∠BOC=∠AOD=150°,
由题意可得:.
故选:A.
【点睛】本题考查对顶角相等和由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,找到等量关系,列出相应的方程组.
12.C
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.设桌子的高度为,长方体木块一个面(图中展示的面)的长比宽大,根据图中两种放置的方式,列出二元一次方程组,解之即可得出结论.
【详解】解:设桌子的高度为,长方体木块一个面(图中展示的面)的长比宽大,
由题意得:,
解得:,
∴桌子的高度为,
故选:C.
13.18
【分析】本题考查了二元一次方程组的应用,设每个小长方形的长为x,宽为y,根据题意,得,结合计算即可.
【详解】设每个小长方形的长为x,宽为y,根据题意,得
,
解得
故,
故答案为:18.
14. , , 2000, 1800,
【解析】略
15. 320 360
【分析】本题考查了二元一次方程的应用,理解题意并正确列方程是解题关键.设原计划第一组生产个零件、第二组生产个零件,根据题意列二元一次方程求解即可.
【详解】解:设原计划第一组生产个零件、第二组生产个零件,
则,
解得:,
即原计划第一组生产个零件、第二组生产个零件,
故答案为:320;360.
16. 5 3
【分析】本题考查二元一次方程的解,首先根据题意列出二元一次方程,然后根据题目提供的条件进行求解.
【详解】解:①列出关于x,y的二元一次方程: ;
②当时,则,解得:;
③当时,则,解得:;
故答案为:;5;3.
17. (1) (1+5%)x, (1-15%)y (2),
【解析】略
18.该超市购进种月饼160盒,购进种月饼20盒才能使得获利最大,最大利润是3800元
【分析】设种月饼每盒元,种月饼每盒元,根据两种购买方式建立方程组,解方程组可得的值,再设该超市购进种月饼盒,可获得的利润为元,则该超市购进种月饼盒,从而可得,然后根据两种月饼数量的关系建立不等式组,解不等式组求出的取值范围,从而可得的取值范围,由此即可得.
【详解】解:设种月饼每盒元,种月饼每盒元,
由题意得:,
解得,
即种月饼每盒30元,种月饼每盒60元,
设该超市购进种月饼盒,可获得的利润为元,则该超市购进种月饼盒,
由题意得:,
要求购进种月饼的数量不少于种月饼数量6倍,且不超过B种月饼数量的8倍,
,
解得,
,即,
则当时,取得最大值,最大值为3800,
此时,
答:该超市购进种月饼160盒,购进种月饼20盒才能使得获利最大,最大利润是3800元.
【点睛】本题考查了二元一次方程组的应用、一元一次不等式组的应用,正确建立方程组和不等式组是解题关键.
19.(1)甲队单独完成此项工程需要40天,乙队单独完成此项工程需要15天
(2)与公司派来的乙工程队再合作6天可完成此项工程
【分析】本题考查了一元一次方程的应用,二元一次方程组的应用.解题的关键在于根据题意正确的列方程(组).
(1)设甲队单独完成此项工程需要天,乙队单独完成此项工程需要天,根据题意列出方程组,解方程组,即可求解;
(2)设与公司派来的乙工程队再合作天可完成此项工程的,根据题意列出一元一次方程,解方程,即可求解.
【详解】(1)解:设甲队单独完成此项工程需要天,乙队单独完成此项工程需要天,
根据题意得
解得
答:甲队单独完成此项工程需要40天,乙队单独完成此项工程需要15天
(2)解:设与公司派来的乙工程队再合作天可完成此项工程的,
根据题意得,
解得,
答:与公司派来的乙工程队再合作6天可完成此项工程.
20.一班45人,二班48人
【分析】设一班x人,二班y人,根据“两班共93人”和“二班比你们一班多交了12元的车费.”列出方程组,解方程组即可.
【详解】解:设一班x人,二班y人,
则 ,
解得:,
即一班45人,二班48人.
答:一班45人,二班48人.
【点睛】此题考查了二元一次方程组的实际应用,读懂题意,找出等量关系列出方程组是解题的关键.
21.7.5尺
【分析】本题考查了二元一次方程组的应用以及数学常识,设绳子长x尺,长木长y尺,根据“用一根绳子去量一根长木,绳子还剩余5.5尺,将绳子对折再量长木,长木还剩余1尺”,可得出关于x,y的二元一次方程组,解方程组即可.
【详解】解:设绳子长x尺,长木长y尺,
依题意,得:,
解得,
答:木长7.5尺.
22.(1)甲、乙两种洗手液的单价分别为18元/瓶,30元/瓶
(2)6天
【分析】本题主要考查二元一次方程组的应用,解题的关键是理解题意;
(1)设甲种洗手液的单价为x元,乙种洗手液的单价为y元,由题意可得方程组,解方程组即可得解;
(2)设七年级采购甲、乙两种洗手液各m瓶,n瓶,由题意易得,然后进行求解即可.
【详解】(1)解:设甲种洗手液的单价为x元/瓶,乙种洗手液的单价为y元/瓶,由题意得:
,
解得:,
答:甲、乙两种洗手液的单价分别为18元/瓶,30元/瓶.
(2)解:设七年级采购甲、乙两种洗手液各m瓶,n瓶,由题意得:
,
∴,
∴(天);
答:这批洗手液可使用6天.
23.买1本笔记本需要2元,1支水笔需要4元
【分析】本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.
设买1本笔记本需要元,1支水笔需要元,根据买1本笔记本和4支水笔,共花了18元和买1本笔记本和1支水笔,刚好花了6元,列出二元一次方程组,解方程组即可.
【详解】解:设买1本笔记本需要元,1支水笔需要元,
根据题意,得,
解得;
答:买1本笔记本需要2元,1支水笔需要4元.
24.供应商购进每个“元元”和“宵宵”的进价分别是60元,40元
【分析】本题主要考查了二元一次方程组的实际应用,设供应商购进每个“元元”和“宵宵”的进价分别是x元,y元,根据一个“元元”的进价比一个“宵宵”的进价多20元,并且购买4个“元元”的价格是购买3个“宵宵”价格的2倍列出方程组求解即可.
【详解】解:设供应商购进每个“元元”和“宵宵”的进价分别是x元,y元,
由题意得,,
解得,
答:供应商购进每个“元元”和“宵宵”的进价分别是60元,40元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
