冀教版数学八年级下册期末复习训练卷(含答案)
文档属性
| 名称 | 冀教版数学八年级下册期末复习训练卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 684.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 09:32:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
冀教版数学八年级下册期末复习训练卷
一、单选题
1.(2024八上·汝州月考)已知点关于x轴的对称点为,且在直线上,则( )
A.1 B.5 C. D.
2.(2023八下·樊城期中)如图,在平面直角坐标系中的顶点的坐标分别是,,,则点C的坐标是( )
A. B. C. D.
3.(2024八上·沭阳期末)如图,在平面直角坐标系中,点的坐标为,沿轴向右平移后得到,点的对应点在直线上,则点与其对应点之间的距离( )
A. B. C.3 D.4
4.(2025七下·潮南月考)已知点在轴上,点在轴上,则点的坐标为( )
A. B. C. D.
5.(2024九上·龙岗期中)下列命题中正确的( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.(2025·孝感模拟)为了了解某市参加中考的名学生的身高情况,抽查了其中名学生的身高进行统计分析.下列叙述错误的是( )
A.名学生的身高情况是总体的一个样本
B.名学生的身高情况是总体
C.每名学生是总体的一个个体
D.样本容量是
7.(2024八下·白云期末)在四边形中,,要使四边形 成为平行四边形,则在下列条件中,应增加条件( )
A. B.
C. D.
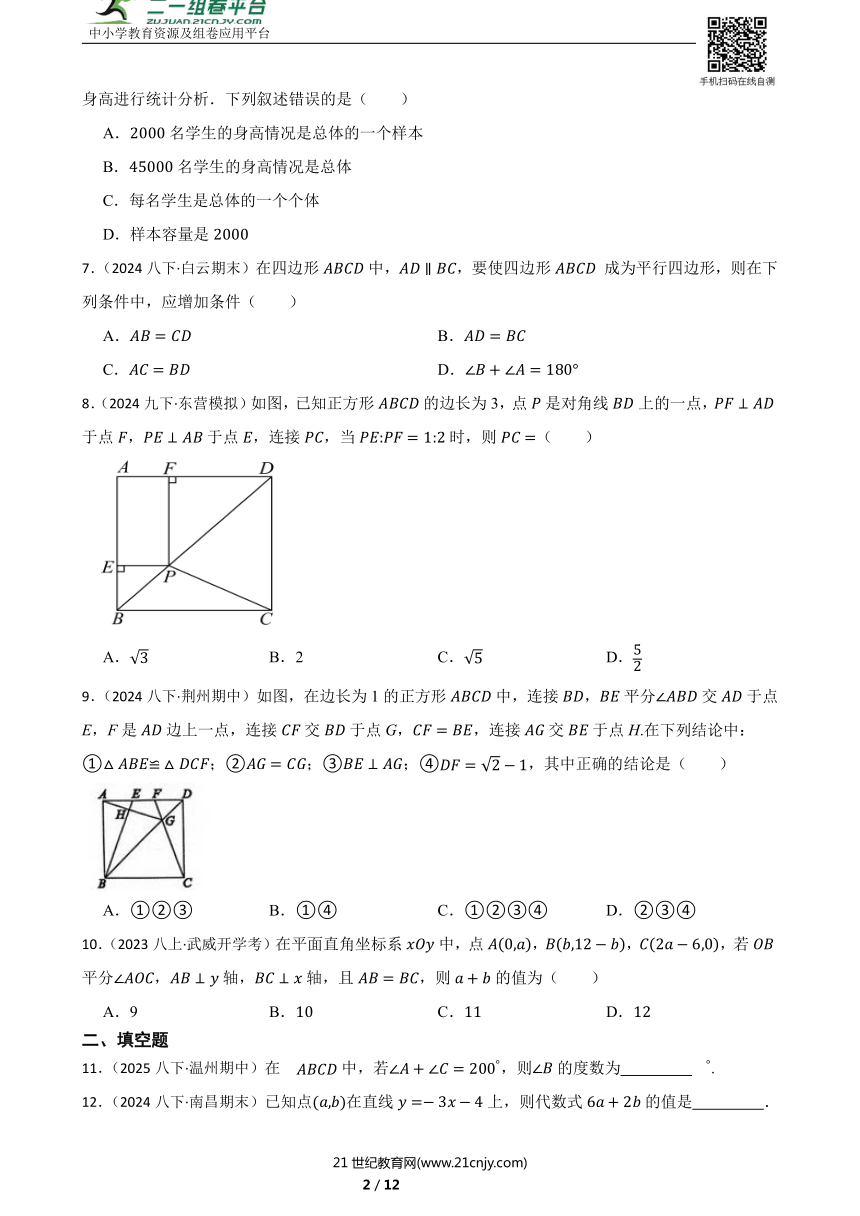
8.(2024九下·东营模拟)如图,已知正方形的边长为3,点是对角线上的一点,于点,于点,连接,当时,则( )
A. B.2 C. D.
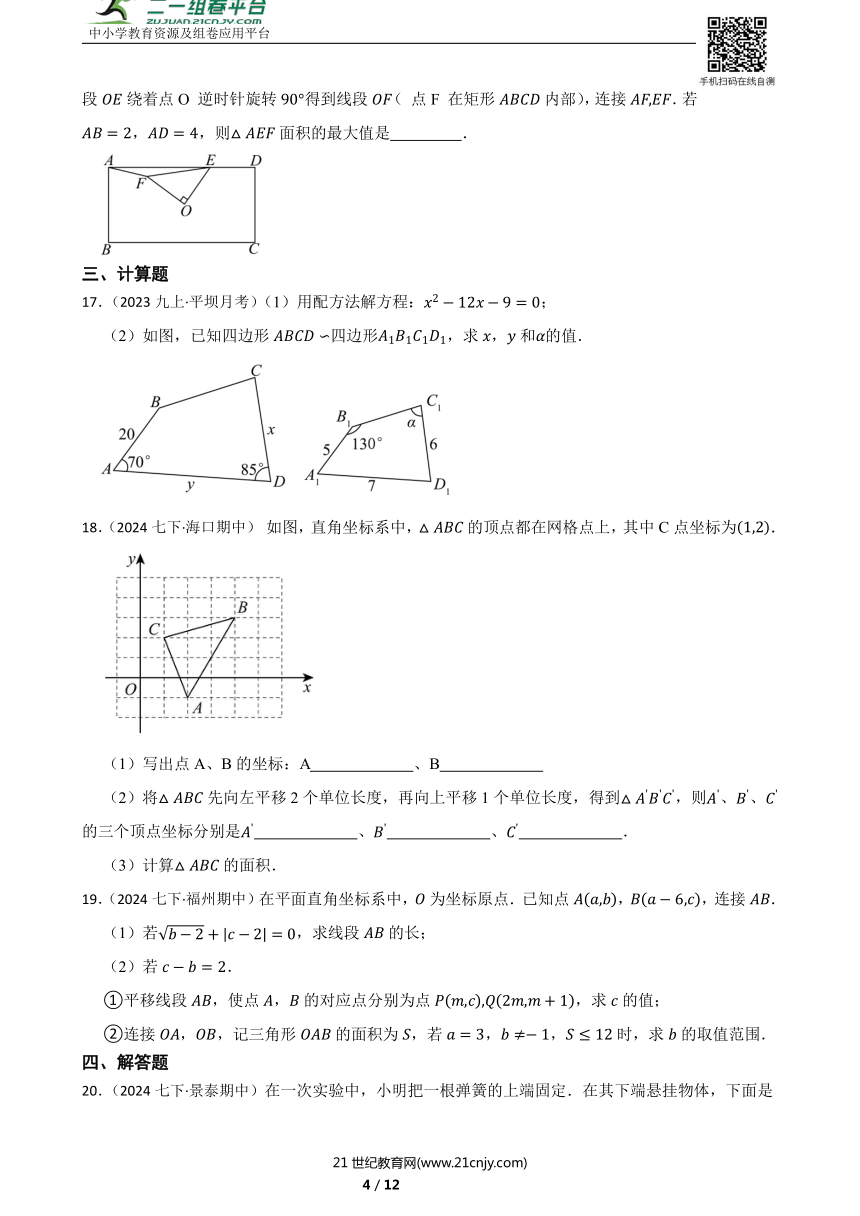
9.(2024八下·荆州期中)如图,在边长为1的正方形中,连接,平分交于点E,F是边上一点,连接交于点G,,连接交于点H.在下列结论中:①;②;③;④,其中正确的结论是( )
A.①②③ B.①④ C.①②③④ D.②③④
10.(2023八上·武威开学考)在平面直角坐标系中,点,,,若平分,轴,轴,且,则的值为( )
A.9 B. C. D.
二、填空题
11.(2025八下·温州期中)在中,若,则的度数为 .
12.(2024八下·南昌期末)已知点在直线上,则代数式的值是 .
13.(2025八下·阜宁月考)如图,将矩形纸片沿边折叠,使点在边中点处.若,则 .
14.(2024八下·海沧期中)如图,P为正方形内一点,过P作直线交于点E,过P作直线交、于G、H,且.若,.以下结论:
①为等边三角形;
②;
③;
④;
其中正确的序号有 .
15.(2024八上·北京市期中)在平面直角坐标系中,已知点对于点和正实数给出如下定义:若,点向右平移个单位,再关于轴对称,得到点;若,点向上平移个单位,再关于轴对称,得到点,称点为点的“-变换”点,点为点的“反-变换”点.例如,已知,,当时,点的“2-变换”点为,点的“2-变换”点为.
(1)当时,
①已知点,则点的“3-变换”点为_______;
②点的“反3-变换”点坐标为_______,点的“反3-变换”点坐标为_______;
(2)已知,记长方形上及内部所有点的“反-变换”点组成的图形面积为.
①当时,_______;
②当时,_______.(用含的式子表示)
16.(2024九下·贵州模拟)如图,O 是矩形 对角线的交点,点E 在 边上,连接,将线段绕着点O 逆时针旋转得到线段( 点F 在矩形内部),连接.若,,则面积的最大值是 .
三、计算题
17.(2023九上·平坝月考)(1)用配方法解方程:;
(2)如图,已知四边形四边形,求,和的值.
18.(2024七下·海口期中) 如图,直角坐标系中,的顶点都在网格点上,其中C点坐标为.
(1)写出点A、B的坐标:A 、B
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到,则、、的三个顶点坐标分别是 、 、 .
(3)计算的面积.
19.(2024七下·福州期中)在平面直角坐标系中,为坐标原点.已知点,,连接.
(1)若,求线段的长;
(2)若.
①平移线段,使点,的对应点分别为点,求的值;
②连接,,记三角形的面积为,若,,时,求的取值范围.
四、解答题
20.(2024七下·景泰期中)在一次实验中,小明把一根弹簧的上端固定.在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体质量的一组对应值.
所挂质量 0 1 2 3 4 5
弹簧长度 18 20 22 24 26 28
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7.5千克时(在允许范围内),你能说出此时的弹簧长度吗?
21.(2024八上·历城月考)在平面直角坐标系中,已知点,点.
(1)若点M在x轴上,求m的值和点M坐标;
(2)若点M到x轴,y轴距离相等,求m的值;
(3)若轴,且,求n的值.
22.(2024·昆明模拟)在平面直角坐标系中,如果点M的横坐标与纵坐标互为相反数,则称点M为智慧点,例如:点,…都是智慧点.
(1)判断函数的图象上是否存在智慧点,若存在,求出其智慧点的坐标;
(2)若二次函数的图象上有且只有一个智慧点,当时,函数的最小值为,最大值为0,求实数n的取值范围.
23.(2024七下·榆林期中)游泳池应定期换水,某游泳池在一次换水前存水936立方米,换水时关闭进水孔打开排水孔,它们的变化情况如表:
放水时间/小时 1 2 3 4 5 6
游泳池的存水量/立方米 858 780 702 624 546 468
根据表格中的数据,回答下列问题:
(1)上表中 是自变量; 是因变量;
(2)当放水时间为1小时时,游泳池的存水是为 立方米;当放水时间为4小时时,游泳池的存水量为 立方米;
(3)说一说这个游泳池的存水量从放水1小时至12小时是怎样变化的;
(4)请你估计当放水5.5小时和9小时时,游泳池的存水量分别是多少立方米?
24.(2024七下·宛城月考)课本上介绍了求多边形的内角和的方法:过边形的一个顶点作对角线,把边形分成个三角形,把求多边形的问题转化成三角形内角和的问题,从而得到边形的内角和等于.现在再提供一种添辅助线的方案,请将方案补充完整,并说明“边形的内角和等于”.
(注:此为时的示意图,说明问题时注意多边形为n边形)
如图,P为n边形.内边上的任意一点(不与点,重合),连接,,…,,那么n边形被分成了( )个三角形,由此推理n边形的内角和定理.
25.(2024八上·广州期中)如图,点,,且,满足.
(1)如图,求,的值;
(2)如图,点在线段上不与、重合移动,,且,猜想线段、、之间的数量关系,并证明你的结论;
(3)若点为轴正半轴上异于原点、点的一个动点,连接,作于点,且,直线交轴于点,当点在轴正半轴上移动时,线段和线段中哪一条线段长为定值,并求出该定值.
答案解析部分
1.【答案】D
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称
2.【答案】C
【知识点】坐标与图形性质;平行四边形的性质
3.【答案】D
【知识点】坐标与图形变化﹣平移;正比例函数的图象
4.【答案】A
【知识点】点的坐标与象限的关系
5.【答案】B
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】C
【知识点】总体、个体、样本、样本容量
7.【答案】B
【知识点】平行四边形的判定
8.【答案】C
【知识点】勾股定理;矩形的性质;正方形的性质;三角形全等的判定-SAS
9.【答案】C
【知识点】等腰三角形的判定与性质;勾股定理;正方形的性质;三角形全等的判定-SAS;三角形全等的判定-ASA
10.【答案】D
【知识点】点的坐标;坐标与图形性质
11.【答案】80
【知识点】平行四边形的性质
12.【答案】
【知识点】一次函数的性质;求代数式的值-整体代入求值
13.【答案】
【知识点】勾股定理;矩形的性质
14.【答案】①②④
【知识点】三角形全等及其性质;含30°角的直角三角形;勾股定理;正方形的性质
15.【答案】(1)①;②或,.
(2)①;②.
【知识点】点的坐标;坐标与图形变化﹣对称;坐标与图形变化﹣平移
16.【答案】
【知识点】二次函数的最值;矩形的性质;旋转的性质;三角形全等的判定-AAS
17.【答案】(1)(2),,
【知识点】配方法解一元二次方程;多边形内角与外角;相似多边形
18.【答案】(1)、
(2)、、
(3)
【知识点】点的坐标;三角形的面积;坐标与图形变化﹣平移;作图﹣平移
19.【答案】(1)6
(2)①;②且
【知识点】一元一次不等式的应用;坐标与图形性质;坐标与图形变化﹣平移;算术平方根的性质(双重非负性)
20.【答案】(1)弹簧的长度与所挂物体质量;所挂物体质量是自变量;弹簧的长度是因变量
(2)物体重量为3千克时,弹簧长;不挂重物时长
(3)
【知识点】函数自变量的取值范围;用表格表示变量间的关系
21.【答案】(1);
(2)或
(3)的值为4或2
【知识点】点的坐标;坐标与图形性质
22.【答案】(1)解:点的横坐标和纵坐标互为相反数,则称点为智慧点,
智慧点都在上,
则,
解得,
图象上的智慧点为;
(2)解:二次函数的图象上有且只有一个智慧点,
∴,即有两个相等的实数根,
,
解得①,
将代入得,
②,
联立①②,得,即,
解得:,则,
,
其顶点坐标为,
,
二次函数,开口向上,
,函数有最小值,
令,
解得:或,
时,函数有最小值,最大值为0,
时,函数的最小值为,最大值为0,
实数的取值范围为.
【知识点】一次函数与二元一次方程(组)的关系;二次函数的最值;利用二次函数图象判断一元二次方程根的情况
23.【答案】(1)放水时间;游泳池的存水量
(2)858;624
(3)解:这个游泳池的存水量从放水1小时至12小时是逐渐减少到零.
(4)解:(立方米).
(立方米).
(立方米).
答:估计当放水5.5小时时,游泳池的存水量是507立方米;当放水9小时时.游泳池的存水量是234立方米.
【知识点】常量、变量;用表格表示变量间的关系
24.【答案】
【知识点】多边形的对角线
25.【答案】(1)解:∵,∴,
∴,
∴,,
∴,;
(2)解:,理由如下:如图,过作,交延长线于点,连接,
∴,
∴,
∴,
∵点,,,,
∴点,,
,
∴,
∴,
∴,
∵,,
∴,
∴,
在与中,
,
∴,
∴,
∵,
∴;
(3)解:是定值,如图,作于,在上截取,∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴是定值,该定值是.
【知识点】旋转的性质;偶次方的非负性;绝对值的非负性;完全平方式;三角形全等的判定-SAS;三角形全等的判定-AAS;全等三角形中对应边的关系;全等三角形中对应角的关系
21世纪教育网(www.21cnjy.com)
12 / 12
冀教版数学八年级下册期末复习训练卷
一、单选题
1.(2024八上·汝州月考)已知点关于x轴的对称点为,且在直线上,则( )
A.1 B.5 C. D.
2.(2023八下·樊城期中)如图,在平面直角坐标系中的顶点的坐标分别是,,,则点C的坐标是( )
A. B. C. D.
3.(2024八上·沭阳期末)如图,在平面直角坐标系中,点的坐标为,沿轴向右平移后得到,点的对应点在直线上,则点与其对应点之间的距离( )
A. B. C.3 D.4
4.(2025七下·潮南月考)已知点在轴上,点在轴上,则点的坐标为( )
A. B. C. D.
5.(2024九上·龙岗期中)下列命题中正确的( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
6.(2025·孝感模拟)为了了解某市参加中考的名学生的身高情况,抽查了其中名学生的身高进行统计分析.下列叙述错误的是( )
A.名学生的身高情况是总体的一个样本
B.名学生的身高情况是总体
C.每名学生是总体的一个个体
D.样本容量是
7.(2024八下·白云期末)在四边形中,,要使四边形 成为平行四边形,则在下列条件中,应增加条件( )
A. B.
C. D.
8.(2024九下·东营模拟)如图,已知正方形的边长为3,点是对角线上的一点,于点,于点,连接,当时,则( )
A. B.2 C. D.
9.(2024八下·荆州期中)如图,在边长为1的正方形中,连接,平分交于点E,F是边上一点,连接交于点G,,连接交于点H.在下列结论中:①;②;③;④,其中正确的结论是( )
A.①②③ B.①④ C.①②③④ D.②③④
10.(2023八上·武威开学考)在平面直角坐标系中,点,,,若平分,轴,轴,且,则的值为( )
A.9 B. C. D.
二、填空题
11.(2025八下·温州期中)在中,若,则的度数为 .
12.(2024八下·南昌期末)已知点在直线上,则代数式的值是 .
13.(2025八下·阜宁月考)如图,将矩形纸片沿边折叠,使点在边中点处.若,则 .
14.(2024八下·海沧期中)如图,P为正方形内一点,过P作直线交于点E,过P作直线交、于G、H,且.若,.以下结论:
①为等边三角形;
②;
③;
④;
其中正确的序号有 .
15.(2024八上·北京市期中)在平面直角坐标系中,已知点对于点和正实数给出如下定义:若,点向右平移个单位,再关于轴对称,得到点;若,点向上平移个单位,再关于轴对称,得到点,称点为点的“-变换”点,点为点的“反-变换”点.例如,已知,,当时,点的“2-变换”点为,点的“2-变换”点为.
(1)当时,
①已知点,则点的“3-变换”点为_______;
②点的“反3-变换”点坐标为_______,点的“反3-变换”点坐标为_______;
(2)已知,记长方形上及内部所有点的“反-变换”点组成的图形面积为.
①当时,_______;
②当时,_______.(用含的式子表示)
16.(2024九下·贵州模拟)如图,O 是矩形 对角线的交点,点E 在 边上,连接,将线段绕着点O 逆时针旋转得到线段( 点F 在矩形内部),连接.若,,则面积的最大值是 .
三、计算题
17.(2023九上·平坝月考)(1)用配方法解方程:;
(2)如图,已知四边形四边形,求,和的值.
18.(2024七下·海口期中) 如图,直角坐标系中,的顶点都在网格点上,其中C点坐标为.
(1)写出点A、B的坐标:A 、B
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到,则、、的三个顶点坐标分别是 、 、 .
(3)计算的面积.
19.(2024七下·福州期中)在平面直角坐标系中,为坐标原点.已知点,,连接.
(1)若,求线段的长;
(2)若.
①平移线段,使点,的对应点分别为点,求的值;
②连接,,记三角形的面积为,若,,时,求的取值范围.
四、解答题
20.(2024七下·景泰期中)在一次实验中,小明把一根弹簧的上端固定.在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体质量的一组对应值.
所挂质量 0 1 2 3 4 5
弹簧长度 18 20 22 24 26 28
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7.5千克时(在允许范围内),你能说出此时的弹簧长度吗?
21.(2024八上·历城月考)在平面直角坐标系中,已知点,点.
(1)若点M在x轴上,求m的值和点M坐标;
(2)若点M到x轴,y轴距离相等,求m的值;
(3)若轴,且,求n的值.
22.(2024·昆明模拟)在平面直角坐标系中,如果点M的横坐标与纵坐标互为相反数,则称点M为智慧点,例如:点,…都是智慧点.
(1)判断函数的图象上是否存在智慧点,若存在,求出其智慧点的坐标;
(2)若二次函数的图象上有且只有一个智慧点,当时,函数的最小值为,最大值为0,求实数n的取值范围.
23.(2024七下·榆林期中)游泳池应定期换水,某游泳池在一次换水前存水936立方米,换水时关闭进水孔打开排水孔,它们的变化情况如表:
放水时间/小时 1 2 3 4 5 6
游泳池的存水量/立方米 858 780 702 624 546 468
根据表格中的数据,回答下列问题:
(1)上表中 是自变量; 是因变量;
(2)当放水时间为1小时时,游泳池的存水是为 立方米;当放水时间为4小时时,游泳池的存水量为 立方米;
(3)说一说这个游泳池的存水量从放水1小时至12小时是怎样变化的;
(4)请你估计当放水5.5小时和9小时时,游泳池的存水量分别是多少立方米?
24.(2024七下·宛城月考)课本上介绍了求多边形的内角和的方法:过边形的一个顶点作对角线,把边形分成个三角形,把求多边形的问题转化成三角形内角和的问题,从而得到边形的内角和等于.现在再提供一种添辅助线的方案,请将方案补充完整,并说明“边形的内角和等于”.
(注:此为时的示意图,说明问题时注意多边形为n边形)
如图,P为n边形.内边上的任意一点(不与点,重合),连接,,…,,那么n边形被分成了( )个三角形,由此推理n边形的内角和定理.
25.(2024八上·广州期中)如图,点,,且,满足.
(1)如图,求,的值;
(2)如图,点在线段上不与、重合移动,,且,猜想线段、、之间的数量关系,并证明你的结论;
(3)若点为轴正半轴上异于原点、点的一个动点,连接,作于点,且,直线交轴于点,当点在轴正半轴上移动时,线段和线段中哪一条线段长为定值,并求出该定值.
答案解析部分
1.【答案】D
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称
2.【答案】C
【知识点】坐标与图形性质;平行四边形的性质
3.【答案】D
【知识点】坐标与图形变化﹣平移;正比例函数的图象
4.【答案】A
【知识点】点的坐标与象限的关系
5.【答案】B
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】C
【知识点】总体、个体、样本、样本容量
7.【答案】B
【知识点】平行四边形的判定
8.【答案】C
【知识点】勾股定理;矩形的性质;正方形的性质;三角形全等的判定-SAS
9.【答案】C
【知识点】等腰三角形的判定与性质;勾股定理;正方形的性质;三角形全等的判定-SAS;三角形全等的判定-ASA
10.【答案】D
【知识点】点的坐标;坐标与图形性质
11.【答案】80
【知识点】平行四边形的性质
12.【答案】
【知识点】一次函数的性质;求代数式的值-整体代入求值
13.【答案】
【知识点】勾股定理;矩形的性质
14.【答案】①②④
【知识点】三角形全等及其性质;含30°角的直角三角形;勾股定理;正方形的性质
15.【答案】(1)①;②或,.
(2)①;②.
【知识点】点的坐标;坐标与图形变化﹣对称;坐标与图形变化﹣平移
16.【答案】
【知识点】二次函数的最值;矩形的性质;旋转的性质;三角形全等的判定-AAS
17.【答案】(1)(2),,
【知识点】配方法解一元二次方程;多边形内角与外角;相似多边形
18.【答案】(1)、
(2)、、
(3)
【知识点】点的坐标;三角形的面积;坐标与图形变化﹣平移;作图﹣平移
19.【答案】(1)6
(2)①;②且
【知识点】一元一次不等式的应用;坐标与图形性质;坐标与图形变化﹣平移;算术平方根的性质(双重非负性)
20.【答案】(1)弹簧的长度与所挂物体质量;所挂物体质量是自变量;弹簧的长度是因变量
(2)物体重量为3千克时,弹簧长;不挂重物时长
(3)
【知识点】函数自变量的取值范围;用表格表示变量间的关系
21.【答案】(1);
(2)或
(3)的值为4或2
【知识点】点的坐标;坐标与图形性质
22.【答案】(1)解:点的横坐标和纵坐标互为相反数,则称点为智慧点,
智慧点都在上,
则,
解得,
图象上的智慧点为;
(2)解:二次函数的图象上有且只有一个智慧点,
∴,即有两个相等的实数根,
,
解得①,
将代入得,
②,
联立①②,得,即,
解得:,则,
,
其顶点坐标为,
,
二次函数,开口向上,
,函数有最小值,
令,
解得:或,
时,函数有最小值,最大值为0,
时,函数的最小值为,最大值为0,
实数的取值范围为.
【知识点】一次函数与二元一次方程(组)的关系;二次函数的最值;利用二次函数图象判断一元二次方程根的情况
23.【答案】(1)放水时间;游泳池的存水量
(2)858;624
(3)解:这个游泳池的存水量从放水1小时至12小时是逐渐减少到零.
(4)解:(立方米).
(立方米).
(立方米).
答:估计当放水5.5小时时,游泳池的存水量是507立方米;当放水9小时时.游泳池的存水量是234立方米.
【知识点】常量、变量;用表格表示变量间的关系
24.【答案】
【知识点】多边形的对角线
25.【答案】(1)解:∵,∴,
∴,
∴,,
∴,;
(2)解:,理由如下:如图,过作,交延长线于点,连接,
∴,
∴,
∴,
∵点,,,,
∴点,,
,
∴,
∴,
∴,
∵,,
∴,
∴,
在与中,
,
∴,
∴,
∵,
∴;
(3)解:是定值,如图,作于,在上截取,∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴是定值,该定值是.
【知识点】旋转的性质;偶次方的非负性;绝对值的非负性;完全平方式;三角形全等的判定-SAS;三角形全等的判定-AAS;全等三角形中对应边的关系;全等三角形中对应角的关系
21世纪教育网(www.21cnjy.com)
12 / 12
同课章节目录
