专题06:四则混合运算与简便计算(专项训练)(含解析)-2025年小升初数学复习专项(人教版)
文档属性
| 名称 | 专题06:四则混合运算与简便计算(专项训练)(含解析)-2025年小升初数学复习专项(人教版) |

|
|
| 格式 | doc | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览




文档简介
/ 让教学更有效 精品试卷 | 数学学科
专题06:四则混合运算与简便计算(专项训练)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.在探究运算律的过程中,我们经历了( )的学习过程。
A.观察猜想一总结应用一举例验证
B.举例验证一观察猜想一总结应用
C.举例验证一总结应用一观察猜想
D.观察猜想一举例验证一总结应用
2.如果4a=b÷2=c,(a、b、c都大于0)则它们的大小关系为( )。
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
3.甲数÷=乙数×,甲数和乙数的关系( )。
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数
4.与竖式计算过程完全一样的算式是( )。
A.28×6×2 B.28×2+28×10
C.8×12+20×12 D.2×28+1×28
5.与1+3+5+7+9+11+13+7+5+3+1表示相同结果的算式是( )。
A.42 B.72-42 C.72 D.72+42
6.计算125×48时,运用了乘法结合律的是( ),运用了乘法分配律的是( )。
①125×40+8 ②125×40+125×8 ③125×8×6
A.①③ B.①② C.③②
二、填空题
7.在□里填上合适的字母或数,在○里填上合适的运算符号。
(1)运用乘法分配律:a×b+b×c=□○(□○□)
(2)运用乘法结合律:25×12=□○□○□
8.明明用计算器计算1.58×24时,发现计算器上的按键“2”损坏了。你能帮助明明想一个用计算器算出结果的方法吗?你的方法( )。21·世纪*教育网
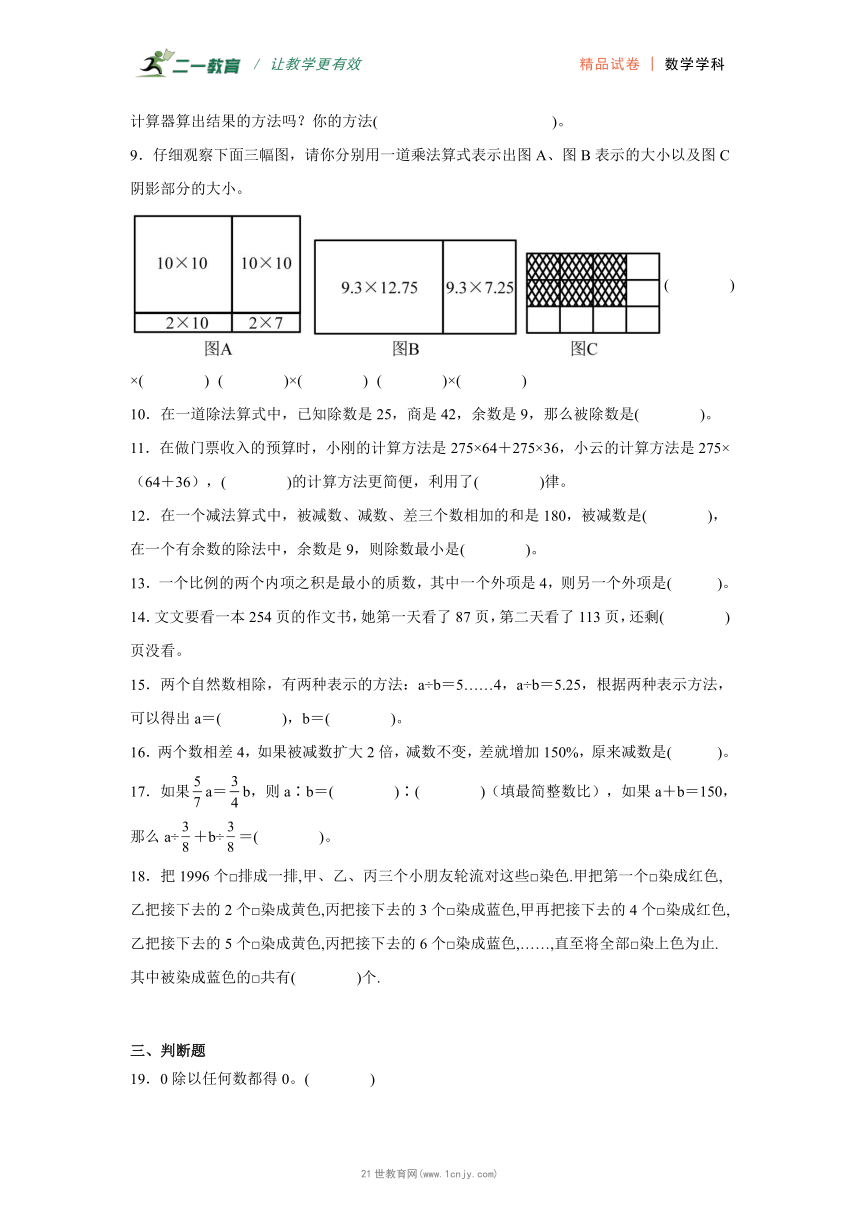
9.仔细观察下面三幅图,请你分别用一道乘法算式表示出图A、图B表示的大小以及图C阴影部分的大小。
( )×( ) ( )×( ) ( )×( )【版权所有:21教育】
10.在一道除法算式中,已知除数是25,商是42,余数是9,那么被除数是( )。
11.在做门票收入的预算时,小刚的计算方法是275×64+275×36,小云的计算方法是275×(64+36),( )的计算方法更简便,利用了( )律。
12.在一个减法算式中,被减数、减数、差三个数相加的和是180,被减数是( ),在一个有余数的除法中,余数是9,则除数最小是( )。
13.一个比例的两个内项之积是最小的质数,其中一个外项是4,则另一个外项是( )。
14.文文要看一本254页的作文书,她第一天看了87页,第二天看了113页,还剩( )页没看。
15.两个自然数相除,有两种表示的方法:a÷b=5……4,a÷b=5.25,根据两种表示方法,可以得出a=( ),b=( )。
16.两个数相差4,如果被减数扩大2倍,减数不变,差就增加150%,原来减数是( )。
17.如果a=b,则a∶b=( )∶( )(填最简整数比),如果a+b=150,那么a÷+b÷=( )。
18.把1996个□排成一排,甲、乙、丙三个小朋友轮流对这些□染色.甲把第一个□染成红色,乙把接下去的2个□染成黄色,丙把接下去的3个□染成蓝色,甲再把接下去的4个□染成红色,乙把接下去的5个□染成黄色,丙把接下去的6个□染成蓝色,……,直至将全部□染上色为止.其中被染成蓝色的□共有( )个.
三、判断题
19.0除以任何数都得0。( )
20.26×(100-1)=26×100-1。( )
21.999×999+1999=1000×1000是应用了运算律,使计算简便。( )
22.计算68×99可以写成68×100-1。( )
23.计算可以想成50个101。( )
四、计算题
24.用你喜欢的方法计算。
9.18÷1.7+40.5÷9
6000-5740÷28×29 20.01×83+17×20.01
25.计算下面各题,能简算的要简算。
(1)900-90÷45+45 (2)5.7-3.82-0.18+5.3 (3)9898-95×101
(4) (5) (6)
五、解答题
26.南北水果店购进一批香蕉和梨,每箱都是25千克,购进香蕉16箱,梨14箱,一共购进多少千克香蕉和梨?21cnjy.com
27.学校图书室的李阿姨在新华书店购买了《地球的奥秘》和《宇宙的起源》各8本,《地球的奥秘》每本8.3元,《宇宙的起源》每本11.9元,李阿姨购买这些书一共花了多少元?
28.某超市开展促销活动,水果类商品每满100元减40元。陈阿姨到超市购买12元/千克的葡萄和8元/千克的香蕉各5.4千克,陈阿姨买这两种水果实际需要支付多少元?
29.汽车上山的速度是每小时36千米,行驶5小时到达山顶,下山时按原路返回,用了4小时。汽车下山时平均每小时比上山多行驶多少千米?21·cn·jy·com
30.妈妈去超市买水果,她手机微信余额里有70元,买葡萄用了24.24元,买西瓜用了33.76元,她手机微信余额还剩多少钱?
31.为了让同学们更深入了解“惊蛰”,四(1)班开展踏青研学活动,需要提前定制统一的帽子和文化衫40套,四(1)班购买帽子和文化衫一共要花多少钱?
帽子15元/个,文化衫45元/件。
32.两辆货车从薛城同时出发,分别向东、西两个方向开出。大货车的速度是105千米/时,小货车的速度是98千米/时。5小时后,两辆货车一共行驶了多少千米?(先画图整理条件和问题,再解答。)
(1)我来画图整理条件和问题:
(2)我的解答:
33.学校号召学生将自家多余的塑料瓶收集起来,变废为宝循环利用。四(9)班学生平均分成三个小组,每个小组11人。第一小组平均每人回收8个塑料瓶;第二小组平均每人回收12个塑料瓶;第三小组平均每人回收26个塑料瓶。这三个小组一共回收多少个塑料瓶?
《专题06:四则混合运算与简便计算(专项训练)-2025年小升初数学复习讲练测(通用版)》参考答案
1.D
【分析】观察猜想、举例验证、总结应用是找出规律的途径。
【详解】在探究运算律的过程中,我们经历了观察猜想、举例验证、总结应用的学习过程。
故答案为:D
【点睛】此题主要考查了数学常识,要熟练掌握。
2.D
【分析】观察算式可知,三个算式的得数相等,可以设它们的得数都是1;然后根据被除数=商×除数,因数=积÷另一个因数,分别求出a、b、c的值,再比较大小,得出结论。
【详解】设4a=b÷2=c=1。
a=1÷4=0.25
b=1×2=2
c=1
2>1>0.25
b>c>a
故答案为:D
【点睛】运用赋值法,根据乘法、除法中各部分的关系计算出a、b、c的值,直接比较大小,更直观。
3.C
【分析】假设甲数÷=乙数×=1,根据“被除数=商×除数”求出甲数,根据“因数=积÷另一个因数”求出乙数,再比较甲数、乙数的大小,得出结论。21*cnjy*com
【详解】假设甲数÷=乙数×=1;
甲数:1×=
乙数:1÷=
<
甲数<乙数
故答案为:C
【点睛】先用假设法设出算式的结果,然后运用乘除法运算中各部分的关系,求出甲、乙数,最后运用分数大小比较的方法比较大小。21教育网
4.B
【分析】整数乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律,用字母表示:(a+b)×c=a×c+b×c;乘法分配律可以逆运用,用字母表示:a×c+b×c=(a+b)×c;将28×12中的12写成(2+10)的形式,根据乘法分配律进行计算即可;据此解答。【来源:21cnj*y.co*m】
【详解】根据分析:
28×12
=28×(2+10)
=28×2+28×10
=56+280
=336
所以与竖式计算过程完全一样的算式是:28×2+28×10。
故答案为:B
5.D
【分析】把1+3+5+7+9+11+13+7+5+3+1中的1+3+5+7和7+5+3+1相加,用(1+7)、(3+5)、(5+3)、(7+1),变成8×4,再加9+11+13,然后与各个算式的结果进行比较,据此即可解答。2·1·c·n·j·y
【详解】1+3+5+7+9+11+13+7+5+3+1
=(1+7)+(3+5)+(5+3)+(7+1)+(9+11)+13
=8×4+20+13
=32+33
=65
A.42=16
B.72-42=49-16=33
C.72=49
D.72+42=49+16=65
所以与1+3+5+7+9+11+13+7+5+3+1表示相同结果的算式是72+42。
故答案为:D
6.C
【分析】乘法结合律:三个数相乘,可以先把前两个数相乘,或者先把后两个数相乘,积不变。用字母表示是(a×b)×c=a×(b×c)。125×48根据乘法结合律可以125×8×6,使得计算简便。21教育名师原创作品
乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。用字母表示是(a+b)×c=a×c+b×c。125×48先写成125×(40+8),再根据乘法分配律可以125×40+125×8,使得计算简便。
【详解】根据分析,计算125×48时,运用了乘法结合律的是125×8×6,符合条件的是③。运用了乘法分配律的是125×40+125×8,符合条件的是②。
故答案为:C
7.(1)b;×;a;+;c
(2)25;×;4;×;3
【分析】(1)两个数与同一个数相乘,可写成这两个数的和与相同数相乘;
(2)先把12拆成4与3的乘积,再利用乘法结合律,先算25与4的乘积,再与3相乘。
【详解】(1)运用乘法分配律:a×b+b×c=b×(a+c);
(2)运用乘法结合律:25×12=25×(4×3)=25×4×3
【点睛】本题考查乘法运算定律,解答本题的关键是掌握乘法运算定律的使用方法。
8.1.58×3×8
【分析】用计算器计算“1.58×24”时,发现计算器的按键“2”坏了,可以把24分解成3×8,然后据乘法结合律(a×b)×c=a×(b×c),再用计算器算出正确结果。
【详解】1.58×24=1.58×(3×8)=1.58×3×8
我的方法是:把1.58×24输入成1.58×3×8,计算结果不变。(答案不唯一)
9. 17 12 9.3 20 6
【分析】图A表示的大小等于4个小长方形的面积相加,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
图B表示的大小等于2个小长方形的面积相加,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
图C阴影部分的大小,先根据分数的意义,得出阴影部分的1份是几分之一,再看有几个这样的分数单位,即用分数单位乘几。
【详解】图A:
10×10+10×7+2×10+2×7
=10×(10+7)+2×(10+7)
=10×17+2×17
=17×(10+2)
=17×12
图B:
9.3×12.75+9.3×7.25
=9.3×(12.75+7.25)
=9.3×20
图C,把大长方形看作单位“1”,平均分成12份,每份表示,这样的6份表示×6。
【点睛】熟练地掌握乘法分配律和分数乘整数的意义是解答本题的关键。
10.1059
【分析】根据除法各部分之间的关系可知,商×除数+余数=被除数。所以用42×25+9可以计算出被除数。
【详解】42×25+9
=1050+9
=1059
所以在一道除法算式中,已知除数是25,商是42,余数是9,那么被除数是1059。
11. 小云 乘法分配
【分析】(1)比较两种计算方法的简便程度:小刚的计算方法是275×64+275×36,需要先分别计算275×64和275×36这两个乘法运算,然后再将所得的积相加,计算过程相对复杂。
小云的计算方法是275×(64+36),先计算括号内的加法64+36=100,再计算275×100,计算过程明显更简便。【出处:21教育名师】
(2)确定运算定律小云的计算方法275×(64+36)=275×64+275×36,符合乘法分配律a×(b+c)=a×b+a×c的形式,据此得解。
【详解】小刚的计算方法是275×64+275×36,小云的计算方法是275×(64+36),通过分析比较这两种算法可以得知,(小云)的计算方法更简便,利用了(乘法分配)律。
12. 90 10
【分析】根据题意,因为被减数=差+减数,所以被减数+减数+差=被减数+被减数=被减数×2=180,180÷2=90;在有余数的除法中,余数都要比除数小,除数要大于余数,即除数>9,最小是10。【来源:21·世纪·教育·网】
【详解】根据分析可知:
180÷2=90
除数>9,即最小是10。
在一个减法算式中,被减数、减数、差三个数相加的和是180,被减数是90,在一个有余数的除法中,余数是9,则除数最小是10。
13./0.5
【分析】根据质数的意义,一个数如果只有1和它本身两个因数,这样的数叫做质数,最小的质数是2。
依据比例的基本性质:两个内项的积等于两个外项的积;已知两个内项的积是最小的质数2,则两个外项的积也是2,用积除以已知的一个外项,求出另一个外项。
【详解】
一个比例的两个内项之积是最小的质数,其中一个外项是4,则另一个外项是()。
14.54
【分析】要求还没看的页数,就用这本书的总页数减去两天看的页数,在计算时可以利用减法的性质简便计算。
【详解】254-87-113
=254-(87+113)
=254-200
=54(页)
所以,还剩54页没看。
15. 84 16
【分析】根据“被除数=商×除数+余数”把a÷b=5……4改写成a=5b+4;
根据“被除数=商×除数”把a÷b=5.25改写成a=5.25b;
据此列出方程:5b+4=5.25b,根据等式的性质解方程,求出b的值;再把b的值代入a=5.25b中,计算出结果,即是a的值。21*cnjy*com
【详解】由a÷b=5……4可得:a=5b+4;
由a÷b=5.25可得:a=5.25b;
5b+4=5.25b
解:5b+4-5b=5.25b-5b
4=0.25b
0.25b÷0.25=4÷0.25
b=16
当b=16时,a=5.25b=5.25×16=84。
可以得出a=84,b=16。
16.2
【分析】设减数为,则被减数是,由题意可知,把原来的差看作单位“1”,后来的差是,根据等量关系式:被减数的2倍-减数=后来的差,据此列方程并求解即可。
【详解】解:设减数为,则被减数是。
两个数相差4,如果被减数扩大2倍,减数不变,差就增加150%,原来减数是2。
【点睛】根据被减数=差+减数,求比一个数多百分之几的数是多少,用乘法计算,找出等量关系式:被减数的2倍-减数=后来的差,据此列方程解答即可。
17. 21 20 400
【分析】假设a=b=1,根据互为倒数的两个数的乘积是1可知,a=,b=,然后用a比上b,再根据比的基本性质进行化简即可;化除法为乘法,把a÷+b÷化为a×+b×,然后根据乘法分配律化为(a+b)×,再把a+b=150代入到式子(a+b)×中进行计算即可。www-2-1-cnjy-com
【详解】假设a=b=1
则a=,b=
a∶b=∶
=(×15)∶(×15)
=21∶20
因为a+b=150
则a÷+b÷
= a×+b×
=(a+b)×
=150×
=400
则如果a=b,则a∶b=21∶20,如果a+b=150,那么a÷+b÷=400。
【点睛】本题考查比的意义,熟练运用比的基本性质是解题的关键。
18.673
【详解】因1+2+3+…+62=,而1996-1953=43.故被染成蓝色的□共有
(3+6+9+…+60)+43=+43=673(个).
19.×
【分析】根据有关0的乘法可知,0乘任何数都得0;根据有关0的除法可知,0不能作除数;据此判断。
【详解】因为0不能作除数,所以0除以任何不是0的数都得0。
原题说法错误。
故答案为:×
20.×
【分析】乘法分配律:两个数的和乘另一个数,等于把这个数分别同两个加数相乘,再把两个积相加,得数不变;据此解答即可。
【详解】26×(100-1)=26×100-26×1,原题说法错误;
故答案为:×。
【点睛】本题利用具体的算式考查了学生对于乘法分配律的理解。
21.√
【分析】先将999写成(1000-1),再根据乘法分配律,将算式变为1000×999-999+1999,根据加法交换律和加法结合律,将算式变为1000×999+(1999-999),再根据乘法分配律,将算式变为1000×(999+1),也就是1000×1000。据此判断。
【详解】999×999+1999
=999×(1000-1)+1999
=1000×999-999+1999
=1000×999+(1999-999)
=1000×999+1000
=1000×(999+1)
=1000×1000
999×999+1999=1000×1000是应用了运算律,使计算简便。说法正确。
故答案为:√
22.×
【分析】计算68×99时,可以把99看成100-1,然后再按照乘法分配律进行计算即可。乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。21世纪教育网版权所有
【详解】68×99
=68×(100-1)
=68×100-68
所以原题说法错误。
故答案为:×
23.√
【分析】观察题干发现,第一个数+最后一个数=101,第二个数+倒数第二个数=101,以此类推,一共有50组101,据此计算即可。
【详解】
故答案为:√。
【点睛】本题主要考查学生的分析能力和总结归纳能力。
24.200;3.15;9.9
55;2001;
【分析】(1)先算括号里面的乘法,再算括号里面的加法,最后算括号外面的除法;
(2)先算乘法,然后将0.375化成,再根据减法的性质a-b-c=a-(b+c)进行简算;
(3)先算两个除法,再算加法;
(4)先算除法,再算乘法,最后算减法;
(5)根据乘法分配律的逆运算a×c+b×c=(a+b)×c进行简算;
(6)中括号里面的根据乘法分配律(a+b)×c=a×c+b×c进行简算,再算中括号外面的乘法。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
=
=
(3)9.18÷1.7+40.5÷9
=5.4+4.5
=9.9
(4)6000-5740÷28×29
=6000-205×29
=6000-5945
=55
(5)20.01×83+17×20.01
=20.01×(83+17)
=20.01×100
=2001
(6)
=
=
=
=
=
25.(1)943;(2)7;(3)303
(4)32;(5);(6)10
【分析】(1)根据运算顺序,先算除法,再从左到右依次计算即可;
(2)按照加法交换律以及减法的性质,把式子转化为5.7+5.3-(3.82+0.18)进行简算;www.21-cn-jy.com
(3)把101看作(100+1),再按照乘法分配律,把式子转化为9898-(95×100+95)进行简算;
(4)按照乘法分配律,把式子转化为424242进行简算;
(5)根据运算顺序,先算小括号里面的减法,再算中括号里面的除法,最后算乘法;
(6)根据除以一个数等于乘它的倒数,把式子转化为,再按照乘法分配律,把式子转化为(7+10+1)计算。
【详解】(1)900-90÷45+45
=900-2+45
=898+45
=943
(2)5.7-3.82-0.18+5.3
=5.7+5.3-(3.82+0.18)
=5.7+5.3-4
=11-4
=7
(3)9898-95×101
=9898-95×(100+1)
=9898-(95×100+95)
=9898-(9500+95)
=9898-9595
=303
(4)
=424242
=36-9+5
=32
(5)
[]
(6)
(7+10+1)
18
=10
26.750千克
【分析】香蕉每箱的重量×香蕉的箱数+梨每箱的重量×梨的箱数=购进香蕉和梨的总重量,计算时可以利用乘法分配进行简算,据此即可解答。
【详解】25×16+25×14
=25×(16+14)
=25×30
=750(千克)
答:一共购进750千克香蕉和梨。
27.161.6元
【分析】根据总价=单价×数量,用《地球的奥秘》每本的单价乘《地球的奥秘》的本数,用《宇宙的起源》每本的单价乘《宇宙的起源》的本数,分别求出买这两类书各花了多少钱,再把买这两类书花的钱加起来,即是李阿姨购买这些书一共花的钱。
【详解】8.3×8+11.9×8
=(8.3+11.9)×8
=20.2×8
=161.6(元)
答:李阿姨购买这些书一共花了161.6元。
【点睛】此题主要根据总价、单价、数量三者之间的关系,利用小数乘法求出结果,注意整数的运算定律同样适用于小数运算。
28.68元
【分析】根据“单价×数量=总价”,分别求出买葡萄、香蕉各自的钱数,再相加,即是总钱数;因为每满100元减40元,看总钱数里面有几个100元,就减去几个40元,即是实际需要支付的钱数。
【详解】12×5.4+8×5.4
=(12+8)×5.4
=20×5.4
=108(元)
108-40=68(元)
答:陈阿姨买这两种水果实际需要支付68元。
29.9千米
【分析】由 速度×时间=路程 可求出山下到山上的路程,即36×5;下山的速度=路程÷下山的时间,即36×5÷4,再用减法求得速度差即可解答。
【详解】36×5÷4
=180÷4
=45(千米)
45-36=9(千米)
答:汽车下山时平均每小时比上山多行驶9千米。
【点睛】本题考查的是对速度、路程、时间三者关系的灵活运用。
30.12元
【分析】根据题意,用妈妈手机微信余额里的70元减去买葡萄和西瓜总共用去的钱,即可求解。
【详解】70-(24.24+33.76)
=70-58
=12(元)
答:她手机微信余额还剩12元钱。
31.2400元
【分析】先算出一套的价钱=一顶帽子的价钱+一件文化衫的价钱,再乘40套即可。
【详解】(15+45)×40
=60×40
=2400(元)
答:四(1)班购买帽子和文化衫一共要花2400元。
32.(1)图见详解
(2)1015千米
【分析】画一条长线段,表示两辆货车一共行驶的路程,再把线段分成两条线段,再把较长的线段平均分成5份,一格表示大货车1小时行驶的路程,5格表示大货5小时行驶的路程,再把较短的线段也平均分成5份,一格表示小货车1小时行驶的路程,5格表示小货5小时行驶的路程,据此画出线段图;路程=速度×时间,把数据代入分别求出大、小货车5小时行驶的路程,然后相加即可解答。2-1-c-n-j-y
【详解】
(1)
(2)105×5+98×5
=525+490
=1015(千米)
答:两辆货车一共行驶了1015千米。
33.506个
【分析】用每个小组平均每人回收的个数乘11,求出每个小组共回收多少个塑料瓶,再相加,就是这三个小组一共回收多少个塑料瓶;在计算过程中发现有相同的因数,可利用乘法分配律进行简算。乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
【详解】11×8+11×12+11×26
=11×(8+12+26)
=11×46
=506(个)
答:这三个小组一共回收506个塑料瓶。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
专题06:四则混合运算与简便计算(专项训练)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.在探究运算律的过程中,我们经历了( )的学习过程。
A.观察猜想一总结应用一举例验证
B.举例验证一观察猜想一总结应用
C.举例验证一总结应用一观察猜想
D.观察猜想一举例验证一总结应用
2.如果4a=b÷2=c,(a、b、c都大于0)则它们的大小关系为( )。
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
3.甲数÷=乙数×,甲数和乙数的关系( )。
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数
4.与竖式计算过程完全一样的算式是( )。
A.28×6×2 B.28×2+28×10
C.8×12+20×12 D.2×28+1×28
5.与1+3+5+7+9+11+13+7+5+3+1表示相同结果的算式是( )。
A.42 B.72-42 C.72 D.72+42
6.计算125×48时,运用了乘法结合律的是( ),运用了乘法分配律的是( )。
①125×40+8 ②125×40+125×8 ③125×8×6
A.①③ B.①② C.③②
二、填空题
7.在□里填上合适的字母或数,在○里填上合适的运算符号。
(1)运用乘法分配律:a×b+b×c=□○(□○□)
(2)运用乘法结合律:25×12=□○□○□
8.明明用计算器计算1.58×24时,发现计算器上的按键“2”损坏了。你能帮助明明想一个用计算器算出结果的方法吗?你的方法( )。21·世纪*教育网
9.仔细观察下面三幅图,请你分别用一道乘法算式表示出图A、图B表示的大小以及图C阴影部分的大小。
( )×( ) ( )×( ) ( )×( )【版权所有:21教育】
10.在一道除法算式中,已知除数是25,商是42,余数是9,那么被除数是( )。
11.在做门票收入的预算时,小刚的计算方法是275×64+275×36,小云的计算方法是275×(64+36),( )的计算方法更简便,利用了( )律。
12.在一个减法算式中,被减数、减数、差三个数相加的和是180,被减数是( ),在一个有余数的除法中,余数是9,则除数最小是( )。
13.一个比例的两个内项之积是最小的质数,其中一个外项是4,则另一个外项是( )。
14.文文要看一本254页的作文书,她第一天看了87页,第二天看了113页,还剩( )页没看。
15.两个自然数相除,有两种表示的方法:a÷b=5……4,a÷b=5.25,根据两种表示方法,可以得出a=( ),b=( )。
16.两个数相差4,如果被减数扩大2倍,减数不变,差就增加150%,原来减数是( )。
17.如果a=b,则a∶b=( )∶( )(填最简整数比),如果a+b=150,那么a÷+b÷=( )。
18.把1996个□排成一排,甲、乙、丙三个小朋友轮流对这些□染色.甲把第一个□染成红色,乙把接下去的2个□染成黄色,丙把接下去的3个□染成蓝色,甲再把接下去的4个□染成红色,乙把接下去的5个□染成黄色,丙把接下去的6个□染成蓝色,……,直至将全部□染上色为止.其中被染成蓝色的□共有( )个.
三、判断题
19.0除以任何数都得0。( )
20.26×(100-1)=26×100-1。( )
21.999×999+1999=1000×1000是应用了运算律,使计算简便。( )
22.计算68×99可以写成68×100-1。( )
23.计算可以想成50个101。( )
四、计算题
24.用你喜欢的方法计算。
9.18÷1.7+40.5÷9
6000-5740÷28×29 20.01×83+17×20.01
25.计算下面各题,能简算的要简算。
(1)900-90÷45+45 (2)5.7-3.82-0.18+5.3 (3)9898-95×101
(4) (5) (6)
五、解答题
26.南北水果店购进一批香蕉和梨,每箱都是25千克,购进香蕉16箱,梨14箱,一共购进多少千克香蕉和梨?21cnjy.com
27.学校图书室的李阿姨在新华书店购买了《地球的奥秘》和《宇宙的起源》各8本,《地球的奥秘》每本8.3元,《宇宙的起源》每本11.9元,李阿姨购买这些书一共花了多少元?
28.某超市开展促销活动,水果类商品每满100元减40元。陈阿姨到超市购买12元/千克的葡萄和8元/千克的香蕉各5.4千克,陈阿姨买这两种水果实际需要支付多少元?
29.汽车上山的速度是每小时36千米,行驶5小时到达山顶,下山时按原路返回,用了4小时。汽车下山时平均每小时比上山多行驶多少千米?21·cn·jy·com
30.妈妈去超市买水果,她手机微信余额里有70元,买葡萄用了24.24元,买西瓜用了33.76元,她手机微信余额还剩多少钱?
31.为了让同学们更深入了解“惊蛰”,四(1)班开展踏青研学活动,需要提前定制统一的帽子和文化衫40套,四(1)班购买帽子和文化衫一共要花多少钱?
帽子15元/个,文化衫45元/件。
32.两辆货车从薛城同时出发,分别向东、西两个方向开出。大货车的速度是105千米/时,小货车的速度是98千米/时。5小时后,两辆货车一共行驶了多少千米?(先画图整理条件和问题,再解答。)
(1)我来画图整理条件和问题:
(2)我的解答:
33.学校号召学生将自家多余的塑料瓶收集起来,变废为宝循环利用。四(9)班学生平均分成三个小组,每个小组11人。第一小组平均每人回收8个塑料瓶;第二小组平均每人回收12个塑料瓶;第三小组平均每人回收26个塑料瓶。这三个小组一共回收多少个塑料瓶?
《专题06:四则混合运算与简便计算(专项训练)-2025年小升初数学复习讲练测(通用版)》参考答案
1.D
【分析】观察猜想、举例验证、总结应用是找出规律的途径。
【详解】在探究运算律的过程中,我们经历了观察猜想、举例验证、总结应用的学习过程。
故答案为:D
【点睛】此题主要考查了数学常识,要熟练掌握。
2.D
【分析】观察算式可知,三个算式的得数相等,可以设它们的得数都是1;然后根据被除数=商×除数,因数=积÷另一个因数,分别求出a、b、c的值,再比较大小,得出结论。
【详解】设4a=b÷2=c=1。
a=1÷4=0.25
b=1×2=2
c=1
2>1>0.25
b>c>a
故答案为:D
【点睛】运用赋值法,根据乘法、除法中各部分的关系计算出a、b、c的值,直接比较大小,更直观。
3.C
【分析】假设甲数÷=乙数×=1,根据“被除数=商×除数”求出甲数,根据“因数=积÷另一个因数”求出乙数,再比较甲数、乙数的大小,得出结论。21*cnjy*com
【详解】假设甲数÷=乙数×=1;
甲数:1×=
乙数:1÷=
<
甲数<乙数
故答案为:C
【点睛】先用假设法设出算式的结果,然后运用乘除法运算中各部分的关系,求出甲、乙数,最后运用分数大小比较的方法比较大小。21教育网
4.B
【分析】整数乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律,用字母表示:(a+b)×c=a×c+b×c;乘法分配律可以逆运用,用字母表示:a×c+b×c=(a+b)×c;将28×12中的12写成(2+10)的形式,根据乘法分配律进行计算即可;据此解答。【来源:21cnj*y.co*m】
【详解】根据分析:
28×12
=28×(2+10)
=28×2+28×10
=56+280
=336
所以与竖式计算过程完全一样的算式是:28×2+28×10。
故答案为:B
5.D
【分析】把1+3+5+7+9+11+13+7+5+3+1中的1+3+5+7和7+5+3+1相加,用(1+7)、(3+5)、(5+3)、(7+1),变成8×4,再加9+11+13,然后与各个算式的结果进行比较,据此即可解答。2·1·c·n·j·y
【详解】1+3+5+7+9+11+13+7+5+3+1
=(1+7)+(3+5)+(5+3)+(7+1)+(9+11)+13
=8×4+20+13
=32+33
=65
A.42=16
B.72-42=49-16=33
C.72=49
D.72+42=49+16=65
所以与1+3+5+7+9+11+13+7+5+3+1表示相同结果的算式是72+42。
故答案为:D
6.C
【分析】乘法结合律:三个数相乘,可以先把前两个数相乘,或者先把后两个数相乘,积不变。用字母表示是(a×b)×c=a×(b×c)。125×48根据乘法结合律可以125×8×6,使得计算简便。21教育名师原创作品
乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。用字母表示是(a+b)×c=a×c+b×c。125×48先写成125×(40+8),再根据乘法分配律可以125×40+125×8,使得计算简便。
【详解】根据分析,计算125×48时,运用了乘法结合律的是125×8×6,符合条件的是③。运用了乘法分配律的是125×40+125×8,符合条件的是②。
故答案为:C
7.(1)b;×;a;+;c
(2)25;×;4;×;3
【分析】(1)两个数与同一个数相乘,可写成这两个数的和与相同数相乘;
(2)先把12拆成4与3的乘积,再利用乘法结合律,先算25与4的乘积,再与3相乘。
【详解】(1)运用乘法分配律:a×b+b×c=b×(a+c);
(2)运用乘法结合律:25×12=25×(4×3)=25×4×3
【点睛】本题考查乘法运算定律,解答本题的关键是掌握乘法运算定律的使用方法。
8.1.58×3×8
【分析】用计算器计算“1.58×24”时,发现计算器的按键“2”坏了,可以把24分解成3×8,然后据乘法结合律(a×b)×c=a×(b×c),再用计算器算出正确结果。
【详解】1.58×24=1.58×(3×8)=1.58×3×8
我的方法是:把1.58×24输入成1.58×3×8,计算结果不变。(答案不唯一)
9. 17 12 9.3 20 6
【分析】图A表示的大小等于4个小长方形的面积相加,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
图B表示的大小等于2个小长方形的面积相加,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
图C阴影部分的大小,先根据分数的意义,得出阴影部分的1份是几分之一,再看有几个这样的分数单位,即用分数单位乘几。
【详解】图A:
10×10+10×7+2×10+2×7
=10×(10+7)+2×(10+7)
=10×17+2×17
=17×(10+2)
=17×12
图B:
9.3×12.75+9.3×7.25
=9.3×(12.75+7.25)
=9.3×20
图C,把大长方形看作单位“1”,平均分成12份,每份表示,这样的6份表示×6。
【点睛】熟练地掌握乘法分配律和分数乘整数的意义是解答本题的关键。
10.1059
【分析】根据除法各部分之间的关系可知,商×除数+余数=被除数。所以用42×25+9可以计算出被除数。
【详解】42×25+9
=1050+9
=1059
所以在一道除法算式中,已知除数是25,商是42,余数是9,那么被除数是1059。
11. 小云 乘法分配
【分析】(1)比较两种计算方法的简便程度:小刚的计算方法是275×64+275×36,需要先分别计算275×64和275×36这两个乘法运算,然后再将所得的积相加,计算过程相对复杂。
小云的计算方法是275×(64+36),先计算括号内的加法64+36=100,再计算275×100,计算过程明显更简便。【出处:21教育名师】
(2)确定运算定律小云的计算方法275×(64+36)=275×64+275×36,符合乘法分配律a×(b+c)=a×b+a×c的形式,据此得解。
【详解】小刚的计算方法是275×64+275×36,小云的计算方法是275×(64+36),通过分析比较这两种算法可以得知,(小云)的计算方法更简便,利用了(乘法分配)律。
12. 90 10
【分析】根据题意,因为被减数=差+减数,所以被减数+减数+差=被减数+被减数=被减数×2=180,180÷2=90;在有余数的除法中,余数都要比除数小,除数要大于余数,即除数>9,最小是10。【来源:21·世纪·教育·网】
【详解】根据分析可知:
180÷2=90
除数>9,即最小是10。
在一个减法算式中,被减数、减数、差三个数相加的和是180,被减数是90,在一个有余数的除法中,余数是9,则除数最小是10。
13./0.5
【分析】根据质数的意义,一个数如果只有1和它本身两个因数,这样的数叫做质数,最小的质数是2。
依据比例的基本性质:两个内项的积等于两个外项的积;已知两个内项的积是最小的质数2,则两个外项的积也是2,用积除以已知的一个外项,求出另一个外项。
【详解】
一个比例的两个内项之积是最小的质数,其中一个外项是4,则另一个外项是()。
14.54
【分析】要求还没看的页数,就用这本书的总页数减去两天看的页数,在计算时可以利用减法的性质简便计算。
【详解】254-87-113
=254-(87+113)
=254-200
=54(页)
所以,还剩54页没看。
15. 84 16
【分析】根据“被除数=商×除数+余数”把a÷b=5……4改写成a=5b+4;
根据“被除数=商×除数”把a÷b=5.25改写成a=5.25b;
据此列出方程:5b+4=5.25b,根据等式的性质解方程,求出b的值;再把b的值代入a=5.25b中,计算出结果,即是a的值。21*cnjy*com
【详解】由a÷b=5……4可得:a=5b+4;
由a÷b=5.25可得:a=5.25b;
5b+4=5.25b
解:5b+4-5b=5.25b-5b
4=0.25b
0.25b÷0.25=4÷0.25
b=16
当b=16时,a=5.25b=5.25×16=84。
可以得出a=84,b=16。
16.2
【分析】设减数为,则被减数是,由题意可知,把原来的差看作单位“1”,后来的差是,根据等量关系式:被减数的2倍-减数=后来的差,据此列方程并求解即可。
【详解】解:设减数为,则被减数是。
两个数相差4,如果被减数扩大2倍,减数不变,差就增加150%,原来减数是2。
【点睛】根据被减数=差+减数,求比一个数多百分之几的数是多少,用乘法计算,找出等量关系式:被减数的2倍-减数=后来的差,据此列方程解答即可。
17. 21 20 400
【分析】假设a=b=1,根据互为倒数的两个数的乘积是1可知,a=,b=,然后用a比上b,再根据比的基本性质进行化简即可;化除法为乘法,把a÷+b÷化为a×+b×,然后根据乘法分配律化为(a+b)×,再把a+b=150代入到式子(a+b)×中进行计算即可。www-2-1-cnjy-com
【详解】假设a=b=1
则a=,b=
a∶b=∶
=(×15)∶(×15)
=21∶20
因为a+b=150
则a÷+b÷
= a×+b×
=(a+b)×
=150×
=400
则如果a=b,则a∶b=21∶20,如果a+b=150,那么a÷+b÷=400。
【点睛】本题考查比的意义,熟练运用比的基本性质是解题的关键。
18.673
【详解】因1+2+3+…+62=,而1996-1953=43.故被染成蓝色的□共有
(3+6+9+…+60)+43=+43=673(个).
19.×
【分析】根据有关0的乘法可知,0乘任何数都得0;根据有关0的除法可知,0不能作除数;据此判断。
【详解】因为0不能作除数,所以0除以任何不是0的数都得0。
原题说法错误。
故答案为:×
20.×
【分析】乘法分配律:两个数的和乘另一个数,等于把这个数分别同两个加数相乘,再把两个积相加,得数不变;据此解答即可。
【详解】26×(100-1)=26×100-26×1,原题说法错误;
故答案为:×。
【点睛】本题利用具体的算式考查了学生对于乘法分配律的理解。
21.√
【分析】先将999写成(1000-1),再根据乘法分配律,将算式变为1000×999-999+1999,根据加法交换律和加法结合律,将算式变为1000×999+(1999-999),再根据乘法分配律,将算式变为1000×(999+1),也就是1000×1000。据此判断。
【详解】999×999+1999
=999×(1000-1)+1999
=1000×999-999+1999
=1000×999+(1999-999)
=1000×999+1000
=1000×(999+1)
=1000×1000
999×999+1999=1000×1000是应用了运算律,使计算简便。说法正确。
故答案为:√
22.×
【分析】计算68×99时,可以把99看成100-1,然后再按照乘法分配律进行计算即可。乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。21世纪教育网版权所有
【详解】68×99
=68×(100-1)
=68×100-68
所以原题说法错误。
故答案为:×
23.√
【分析】观察题干发现,第一个数+最后一个数=101,第二个数+倒数第二个数=101,以此类推,一共有50组101,据此计算即可。
【详解】
故答案为:√。
【点睛】本题主要考查学生的分析能力和总结归纳能力。
24.200;3.15;9.9
55;2001;
【分析】(1)先算括号里面的乘法,再算括号里面的加法,最后算括号外面的除法;
(2)先算乘法,然后将0.375化成,再根据减法的性质a-b-c=a-(b+c)进行简算;
(3)先算两个除法,再算加法;
(4)先算除法,再算乘法,最后算减法;
(5)根据乘法分配律的逆运算a×c+b×c=(a+b)×c进行简算;
(6)中括号里面的根据乘法分配律(a+b)×c=a×c+b×c进行简算,再算中括号外面的乘法。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
=
=
(3)9.18÷1.7+40.5÷9
=5.4+4.5
=9.9
(4)6000-5740÷28×29
=6000-205×29
=6000-5945
=55
(5)20.01×83+17×20.01
=20.01×(83+17)
=20.01×100
=2001
(6)
=
=
=
=
=
25.(1)943;(2)7;(3)303
(4)32;(5);(6)10
【分析】(1)根据运算顺序,先算除法,再从左到右依次计算即可;
(2)按照加法交换律以及减法的性质,把式子转化为5.7+5.3-(3.82+0.18)进行简算;www.21-cn-jy.com
(3)把101看作(100+1),再按照乘法分配律,把式子转化为9898-(95×100+95)进行简算;
(4)按照乘法分配律,把式子转化为424242进行简算;
(5)根据运算顺序,先算小括号里面的减法,再算中括号里面的除法,最后算乘法;
(6)根据除以一个数等于乘它的倒数,把式子转化为,再按照乘法分配律,把式子转化为(7+10+1)计算。
【详解】(1)900-90÷45+45
=900-2+45
=898+45
=943
(2)5.7-3.82-0.18+5.3
=5.7+5.3-(3.82+0.18)
=5.7+5.3-4
=11-4
=7
(3)9898-95×101
=9898-95×(100+1)
=9898-(95×100+95)
=9898-(9500+95)
=9898-9595
=303
(4)
=424242
=36-9+5
=32
(5)
[]
(6)
(7+10+1)
18
=10
26.750千克
【分析】香蕉每箱的重量×香蕉的箱数+梨每箱的重量×梨的箱数=购进香蕉和梨的总重量,计算时可以利用乘法分配进行简算,据此即可解答。
【详解】25×16+25×14
=25×(16+14)
=25×30
=750(千克)
答:一共购进750千克香蕉和梨。
27.161.6元
【分析】根据总价=单价×数量,用《地球的奥秘》每本的单价乘《地球的奥秘》的本数,用《宇宙的起源》每本的单价乘《宇宙的起源》的本数,分别求出买这两类书各花了多少钱,再把买这两类书花的钱加起来,即是李阿姨购买这些书一共花的钱。
【详解】8.3×8+11.9×8
=(8.3+11.9)×8
=20.2×8
=161.6(元)
答:李阿姨购买这些书一共花了161.6元。
【点睛】此题主要根据总价、单价、数量三者之间的关系,利用小数乘法求出结果,注意整数的运算定律同样适用于小数运算。
28.68元
【分析】根据“单价×数量=总价”,分别求出买葡萄、香蕉各自的钱数,再相加,即是总钱数;因为每满100元减40元,看总钱数里面有几个100元,就减去几个40元,即是实际需要支付的钱数。
【详解】12×5.4+8×5.4
=(12+8)×5.4
=20×5.4
=108(元)
108-40=68(元)
答:陈阿姨买这两种水果实际需要支付68元。
29.9千米
【分析】由 速度×时间=路程 可求出山下到山上的路程,即36×5;下山的速度=路程÷下山的时间,即36×5÷4,再用减法求得速度差即可解答。
【详解】36×5÷4
=180÷4
=45(千米)
45-36=9(千米)
答:汽车下山时平均每小时比上山多行驶9千米。
【点睛】本题考查的是对速度、路程、时间三者关系的灵活运用。
30.12元
【分析】根据题意,用妈妈手机微信余额里的70元减去买葡萄和西瓜总共用去的钱,即可求解。
【详解】70-(24.24+33.76)
=70-58
=12(元)
答:她手机微信余额还剩12元钱。
31.2400元
【分析】先算出一套的价钱=一顶帽子的价钱+一件文化衫的价钱,再乘40套即可。
【详解】(15+45)×40
=60×40
=2400(元)
答:四(1)班购买帽子和文化衫一共要花2400元。
32.(1)图见详解
(2)1015千米
【分析】画一条长线段,表示两辆货车一共行驶的路程,再把线段分成两条线段,再把较长的线段平均分成5份,一格表示大货车1小时行驶的路程,5格表示大货5小时行驶的路程,再把较短的线段也平均分成5份,一格表示小货车1小时行驶的路程,5格表示小货5小时行驶的路程,据此画出线段图;路程=速度×时间,把数据代入分别求出大、小货车5小时行驶的路程,然后相加即可解答。2-1-c-n-j-y
【详解】
(1)
(2)105×5+98×5
=525+490
=1015(千米)
答:两辆货车一共行驶了1015千米。
33.506个
【分析】用每个小组平均每人回收的个数乘11,求出每个小组共回收多少个塑料瓶,再相加,就是这三个小组一共回收多少个塑料瓶;在计算过程中发现有相同的因数,可利用乘法分配律进行简算。乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
【详解】11×8+11×12+11×26
=11×(8+12+26)
=11×46
=506(个)
答:这三个小组一共回收506个塑料瓶。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
同课章节目录
